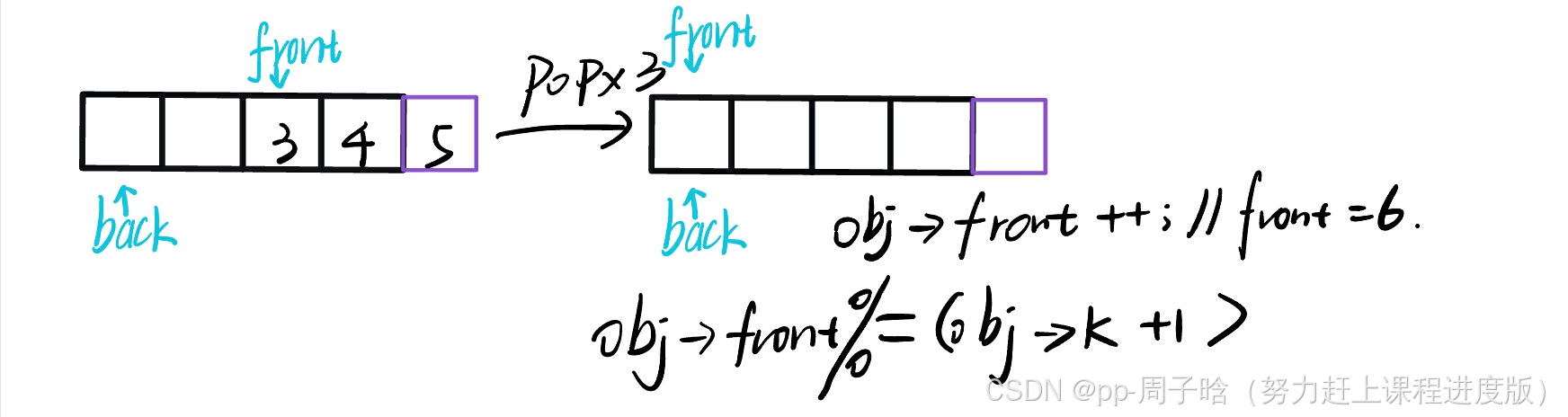Bootstrap

力扣（leetcode）-- 设计循环队列--c语言--数据结构oj题-保姆级分析教程

🎉 揭晓时刻！数据结构与算法探险的栈与队列篇章，即将迎来华丽初谢幕！🎊 这不仅仅是一道题，它是通往智慧殿堂的最后一块拼图，是我们共同征服的又一座小山丘。🏔️

      想象一下，我们正站在知识的海岸线上，眼前是浩瀚无垠的算法海洋，而这道题目，就是引领我们深入探索的最后一艘帆船。🚀 帆已扬起，风正满舵，我们即将扬帆远航，驶向更广阔的天地！

       在这趟旅程的尾声，我将化身为你的魔法导师，用魔法棒（哦不，是键盘）挥洒出无尽的智慧火花。🔮 我们会一起潜入栈与队列的奇妙世界，揭秘那些隐藏在日常编程中的神奇力量。我们会用幽默的语言、生动的例子，还有那些让人拍案叫绝的解题妙招，让这一切变得既有趣又难忘。

       准备好了吗？让我们携手，以最灿烂的笑容和最饱满的热情，迎接这场知识与智慧的盛宴吧！🎉 接下来，就让我们扬帆起航，向着那道题目，全速前进！🚀

题目的完整代码在文章末尾处

此篇文章主要用到 遇到 数组取余 来处理 回绕问题 这样的方法，来解决这道题。

a.往期栈和队列oj题题目解析链接

或者点进我主页就能看到啦。

1.力扣（Leetcode)-栈-有效的括号-c语言-数据结构oj题-CSDN博客

2.力扣（leetcode）-用队列实现栈-c语言-数据结构oj题-CSDN博客

3.力扣（leetcode）--用栈实现队列--c语言--数据结构oj题-CSDN博客

b.题目链接

设计循环队列

c.题目

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

  • MyCircularQueue(k): 构造器，设置队列长度为 k 。
  • Front: 从队首获取元素。如果队列为空，返回 -1 。
  • Rear: 获取队尾元素。如果队列为空，返回 -1 。
  • enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
  • deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
  • isEmpty(): 检查循环队列是否为空。
  • isFull(): 检查循环队列是否已满。

题目所给代码：

typedef struct {  

} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) { }

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) { }

bool myCircularQueueDeQueue(MyCircularQueue* obj) { }   

int myCircularQueueFront(MyCircularQueue* obj) { }

int myCircularQueueRear(MyCircularQueue* obj) { }

bool myCircularQueueIsEmpty(MyCircularQueue* obj) { }

bool myCircularQueueIsFull(MyCircularQueue* obj) { }

void myCircularQueueFree(MyCircularQueue* obj) { }

一、题意解析

a. 需要明白：

1.队列是什么？

具体可见博客 

栈和队列的概念和实现icon-default.png?t=N7T8https://blog.csdn.net/2303_77756141/article/details/140506549?app_version=6.3.9&csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22140506549%22%2C%22source%22%3A%222303_77756141%22%7D&utm_source=app

通过清楚他的概念，现在我们可以开始做题了

2.这道题最重要的就是需要不断的画图，大家都将自己的纸和笔准备好哦。

b.思路

想要实现一个循环队列首先我们可以思考，是使用链表还是数组实现呢，其实现在想一想都还觉得差不多，接下来让我画图为你解释。

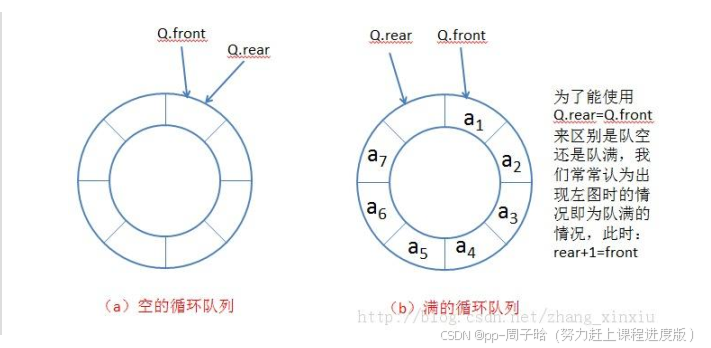
1. 一个循环队列是怎么样的。

我们可以先试着想象一下

但这只是我们的想象，想要实现如图所示的效果的话，我们可以使用数组或者链表。

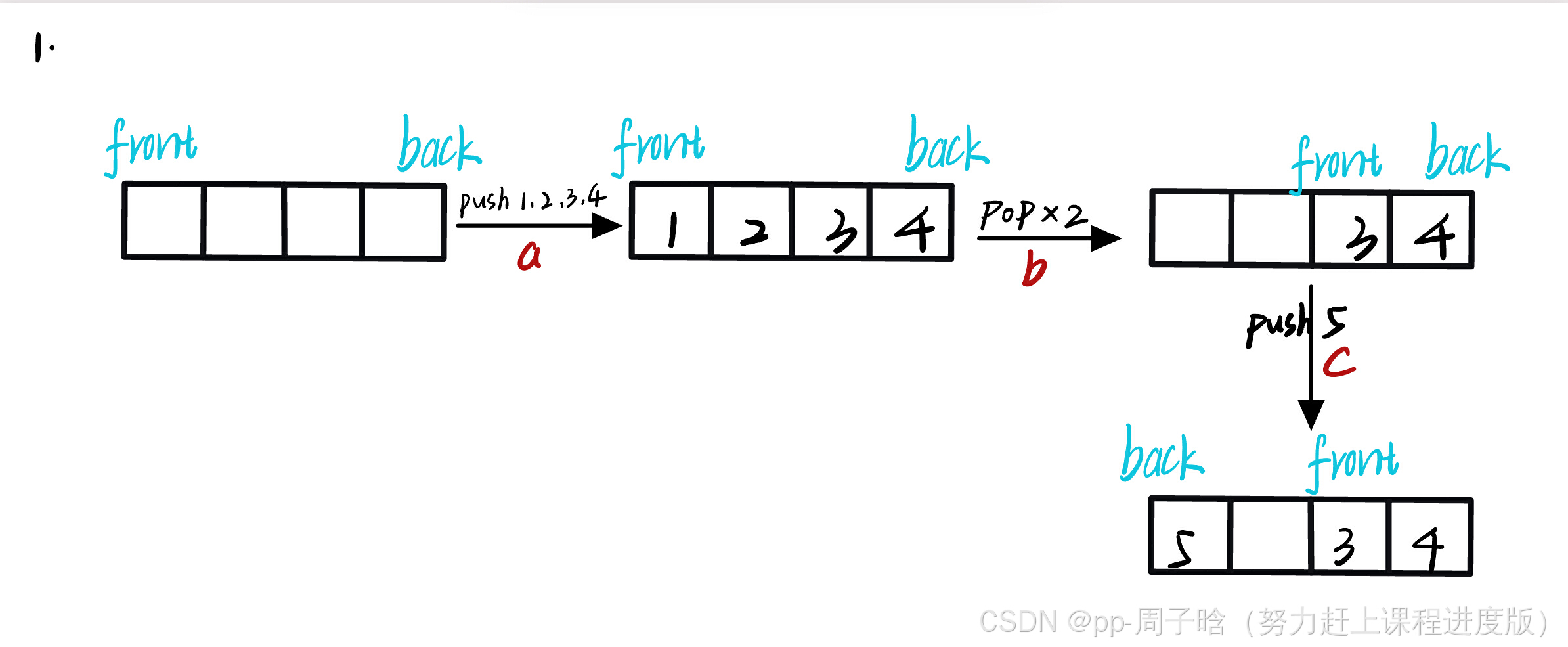
让我们先画图演示一下这个循环队列最初级的过程：我们开辟了四个空间用于存数据，我们先存入四个数据1,、2、3、4，再删除两个数据，再存入一个数据5。

要一直清楚队列的要求哦。

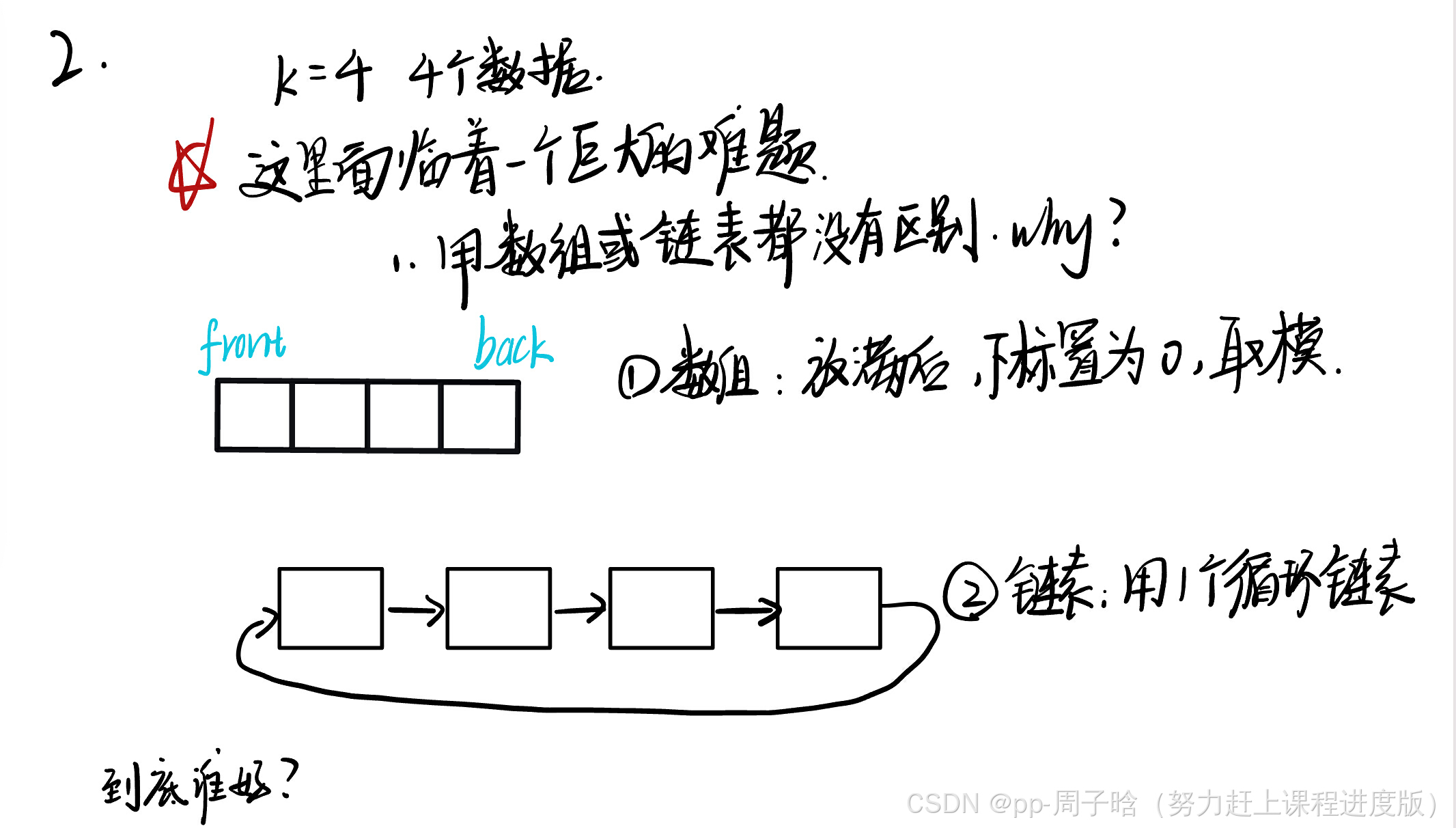
2. 使用数组还是链表来做这道题？

 

事实上到这里我们只清楚，两种方式都可以来做这道题，还无法清楚哪种方式更好。

所以让我们在解决要实现循环队列所需要清楚的几个要求的问题的过程中来一步步挖掘吧。

3.需要解决的几个问题

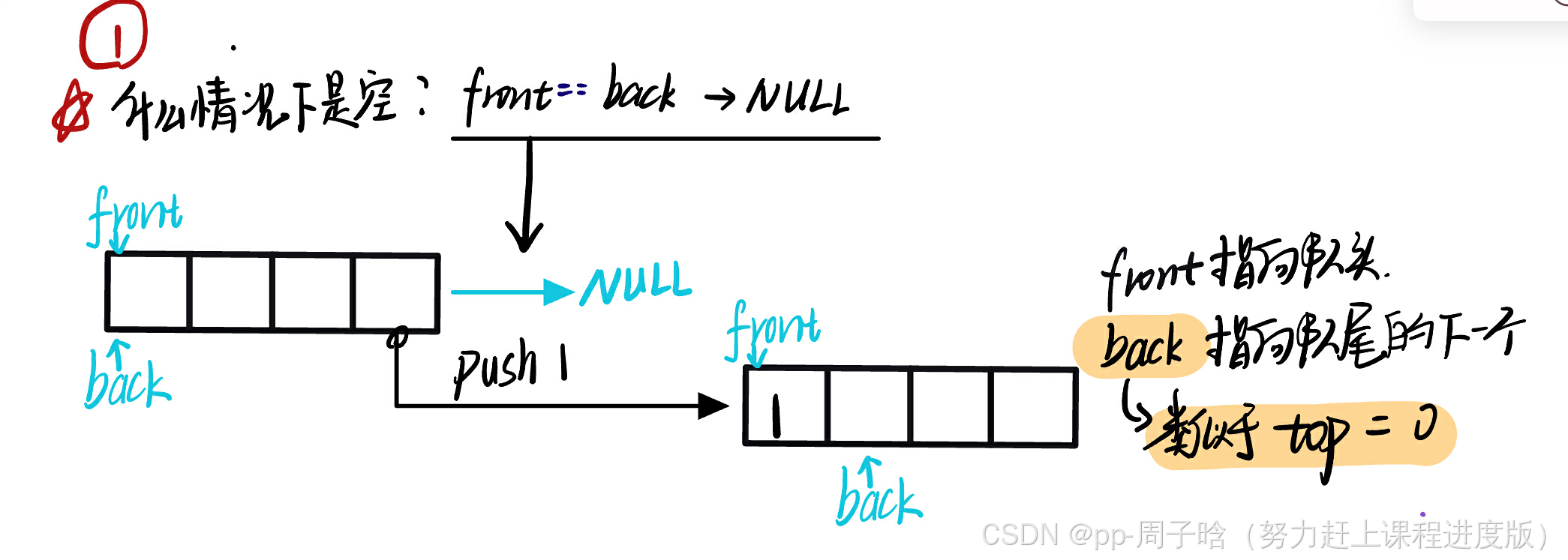
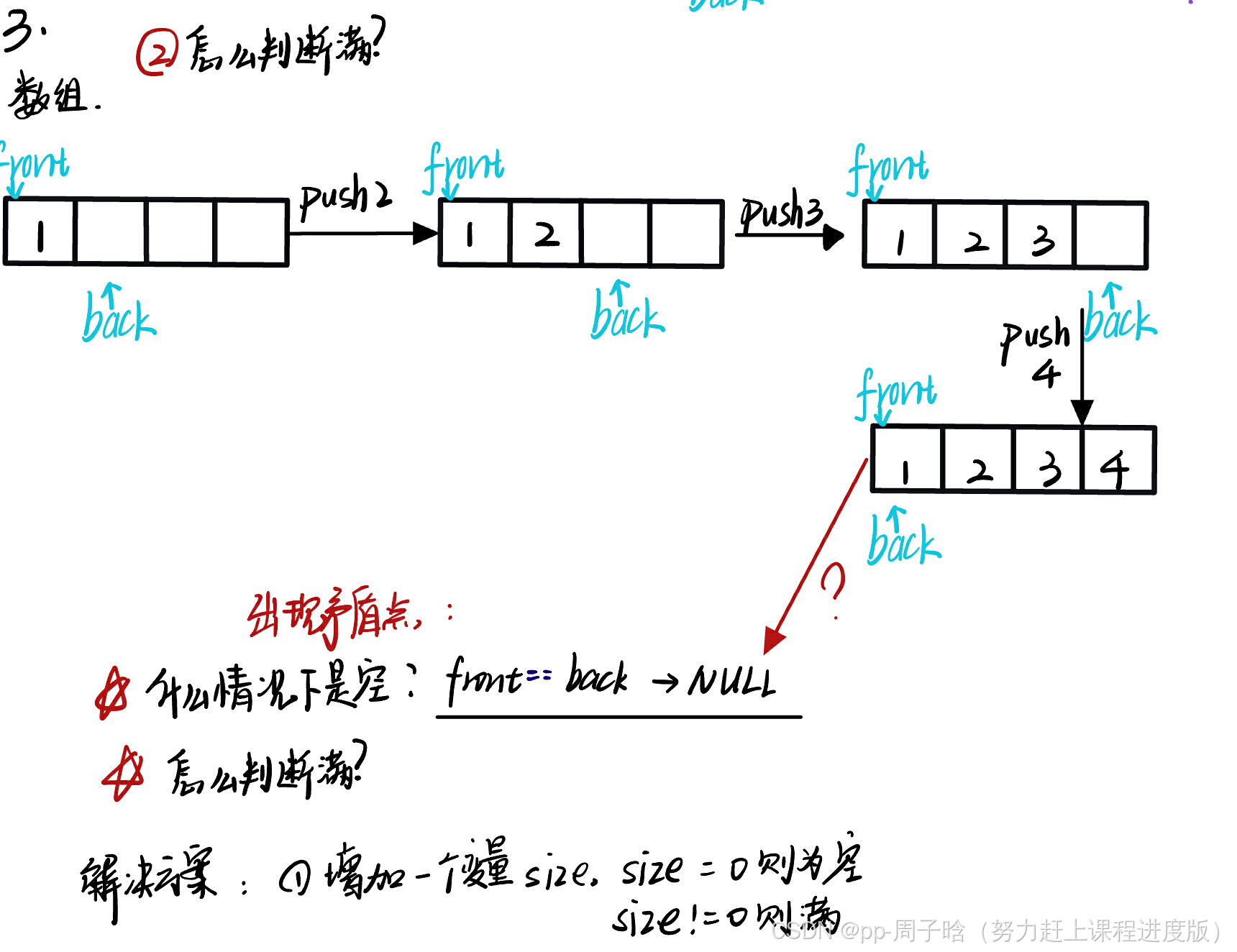
a.什么情况下循环队列为空？

当 front == back时，循环队列是NULL。

使back指向队尾的下一个位置，即进入一个数据之后，给front赋值，back++。

back是不是就类似于实现栈时的 top = 0（表示指向栈顶元素的下一个）。

b.什么时候循环队列满？

如图，我们发现，当循环队列满时，front == back,这时就与循环队列为空的判断形成了矛盾，那我们要如何解决呢。在此我有两个解决方案。

解决方案1

通过增加一个计数变量size，初始size=0,size == 0时，循环队列为空，每增加一个数据，size++ ;当size == k（k是循环队列中我们最多能存的数据个数）时，循环队列满。

解决方案2

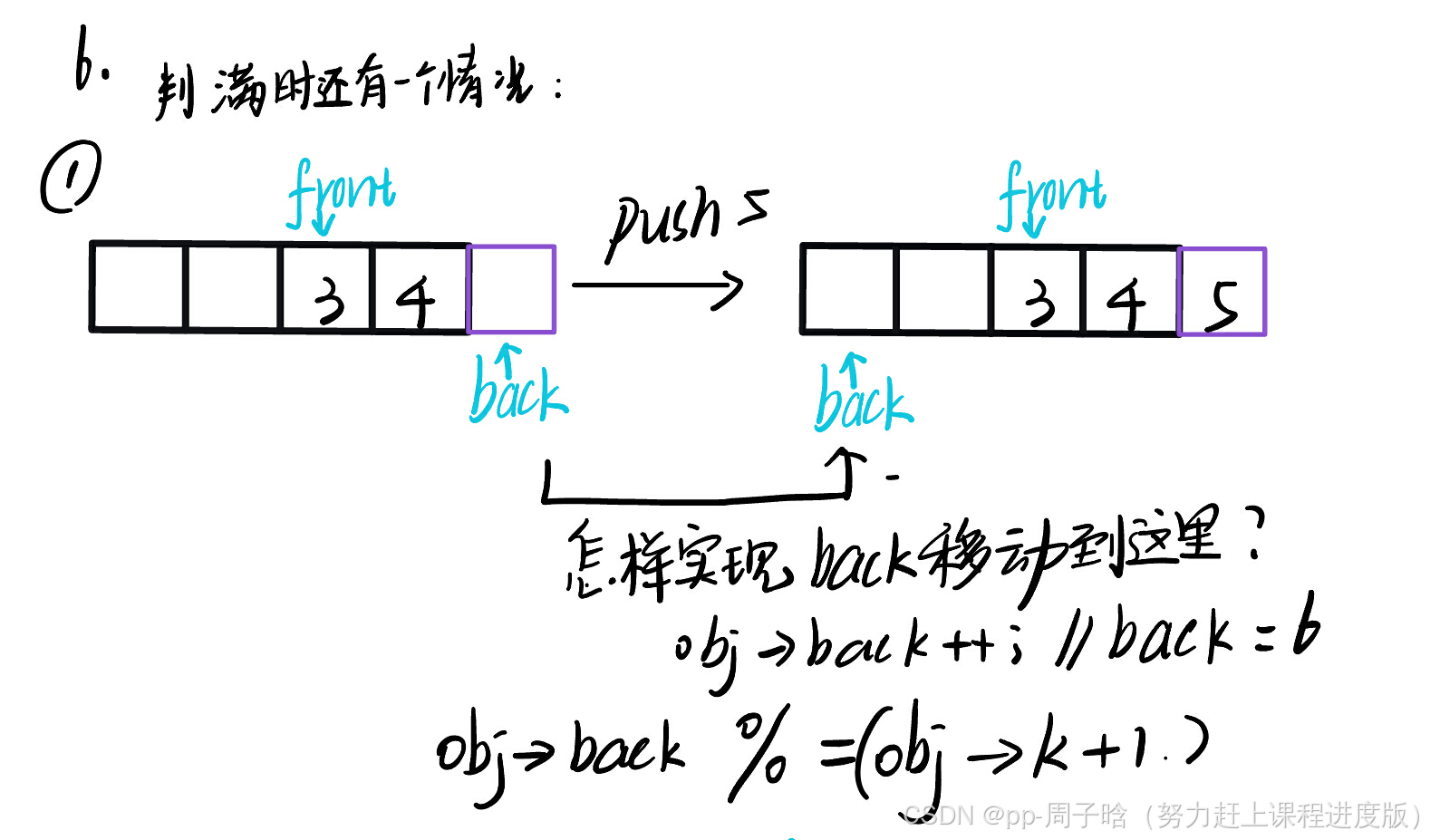
通过多开一个位置， 即k = 4,一共能存4个数据，但是我们开辟5个空间。

如图，如果你认真阅读此图的内容，并且自己画图带入数据的话就能很好理解，为什么我们需要增加一个数据空间了。重点在于：back的位置永远是空的。

总结：

1.什么情况下循环队列为空？front == back

2.什么情况下循环队列满？ (back+1)%（k+1）== front

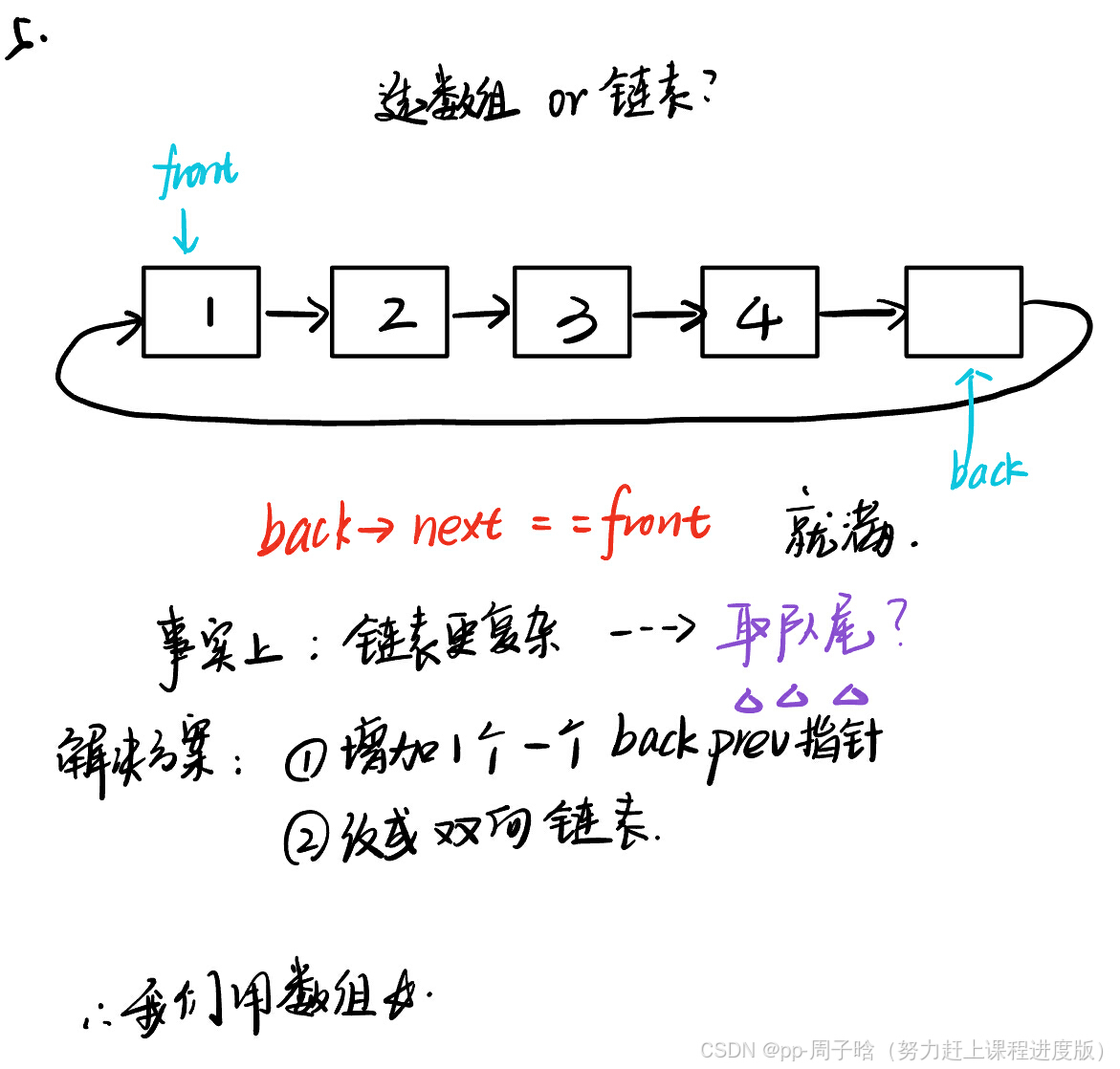
c.再回到使用数组还是链表

看似back->next == front,就可以直接来判断队满，但是还有一个更加现实的问题，

如果要用链表做的话，就必须知道队尾，但是用一个循环链表想要找到他的队尾更复杂

解决方案

1.增加1个backprev的指针。

2.将这个循环链表改成双向链表。

我们还是用数组来解决这道题

二、每个函数实现的具体讲解

1. 定义队列结构体

用于存放一个循环队列相关数据

typedef struct {
    int* a;//数组的指针
    int front;
    int back;
    int k;
} MyCircularQueue;

2. 初始化循环队列

MyCircularQueue* myCircularQueueCreate(int k) {

    //开辟循环队列的空间
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    obj->front = 0;
    obj->back = 0;
    obj->k = k;

    return obj;
}

3.判空

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->back;
}

4.判满

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->back + 1) % (obj->k + 1) == obj->front;
}

5.入队

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (!myCircularQueueIsFull(obj))
    {
        obj->a[obj->back] = value;
        obj->back++;
        obj->back %= (obj->k + 1);//这里为什么要这么写请看图
        return true;
    }
    else
    {
        return false;
    }
}

6.出队

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return false;
    }
    else
    {

        obj->front++;
        obj->front %= (obj->k + 1);//这里为什么要这么写请看图
        return true;
    }

}

在你做了出队入队，是否还有对取余，模的顾虑，疑问？

现在我为你解答：

对于数据小于这个循环队列长度的数据时，取余之后数据是不会有变化的。

在使用数组处理问题时，取余可以解决回绕问题

7.取队头

int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    return obj->a[obj->front];
}
 

8.取队尾

为处理这个越界问题，我们有两种方法，第一种当back为0，即先判断队列是否为空，再判断back是否等于0，若back为0 ，可分析出，队头就是数组中的最后一个数据。因为back不为空的时候，back又为0，数组的最后一个位置一定是有元素的。可以再自己想想看。

int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj))
    {
        return -1;
    }
    //if (obj->back == 0)
    //{
    //    return obj->a[obj->k];
    //}
    //else
    //{
    //    return obj->a[obj->k - 1];
    //}
    return obj->a[(obj->back - 1 + obj->k + 1) % (obj->k + 1)];
}

这样你是否能对取余有一个很好的理解了呢？

整个数组长度5块，将现在的back再加一遍长度，可回到back的上一个元素，一定要清楚back指的是队尾数据的下一个数据。

相当于再走了一遍队列，又减掉这边队列的长度，原来的值不变，因此对于数据小于数组长度的数据，用了这个公式也不会发生改变。

希望你能在阅读完这几个图片之后顿悟

9.此题延伸：小试牛刀

如何设计循环队列的数据个数？

请先思考在解答（如果你已经能理解以上的所有内容，想必这个问题就迎刃而解啦！）

back 在 front 后：obj->back - obj->front;

back 在 front 前：(obj->back + obj->k ) - obj->front

三、完整代码

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
#include<stdbool.h>
#include<stdlib.h>

typedef struct {
	int* a;//数组的指针
	int front;
	int back;
	int k;
} MyCircularQueue;

//初始化循环队列
MyCircularQueue* myCircularQueueCreate(int k) {
	MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
	obj->a = (int*)malloc(sizeof(int) * (k + 1));
	obj->front = 0;
	obj->back = 0;
	obj->k = k;

	return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
	return obj->front == obj->back;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
	return (obj->back + 1) % (obj->k + 1) == obj->front;
}
//插入
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
	if (!myCircularQueueIsFull(obj))
	{
		obj->a[obj->back] = value;
		obj->back++;
		obj->back %= (obj->k + 1);
		return true;
	}
	else
	{
		return false;
	}
}
//删除
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
	if (myCircularQueueIsEmpty(obj))
	{
		return false;
	}
	else
	{

		obj->front++;
		obj->front %= (obj->k + 1);
		return true;
	}

}

int myCircularQueueFront(MyCircularQueue* obj) {
	if (myCircularQueueIsEmpty(obj))
	{
		return -1;
	}
	return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
	if (myCircularQueueIsEmpty(obj))
	{
		return -1;
	}
	//if (obj->back == 0)
	//{
	//	return obj->a[obj->k];
	//}
	//else
	//{
	//	return obj->a[obj->k - 1];
	//}
	return obj->a[(obj->back - 1 + obj->k + 1) % (obj->k + 1)];
}


void myCircularQueueFree(MyCircularQueue* obj) {
	free(obj->a);
	obj->a = NULL;
	free(obj);

}

结语：

       在探索这道题的解答过程中，我深刻体会到知识的海洋浩瀚无垠，每一次解题都是一次自我挑战与成长的宝贵机会。虽然我已经尽力将解题思路和步骤清晰地呈现出来，但深知学无止境，仍有诸多改进和优化的空间。如果您在阅读过程中发现了更好的解法或是有任何疑问和建议，都非常欢迎您在评论区留言，让我们共同探讨，共同进步。

       最后，如果您觉得这篇博客对您有所帮助，或是受到了些许启发，不妨动动手指，给予一个小小的鼓励——点个赞、收藏起来以便日后回顾，甚至分享给更多需要帮助的朋友。您的每一次互动，都是对我最大的支持与鼓励，也是我继续创作更多优质内容的动力源泉。

       再次感谢您的阅读，期待在未来的解题之旅中，与您再次相遇，共同解锁更多知识的奥秘！

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
OrangePi Zero2 全志H616 开发初探
高性能网络通讯框架Netty预热—NIO模型
js理解异步编程和回调
Ubuntu VirtualBox 安装win10报错：FATAL: No bootable medium found! System halted.
MySQL 语法教程
Kotlin版封装网络请求（MVVM+Flow+Retrofit2+Coroutine协程）
RabbitMQ学习笔记：死信交换机DLX
JavaScript 删除数组中指定元素(5种方法)
ABAP:创建/修改客户的银行信息
【题目】2023年全国职业院校技能大赛 GZ073 网络系统管理赛项赛题第8套B模块
;