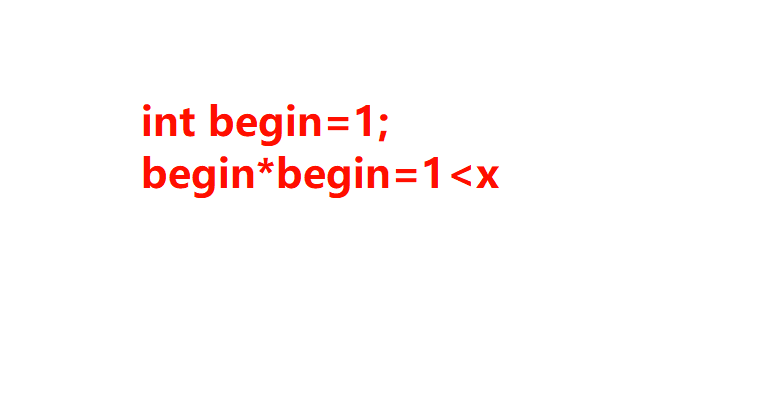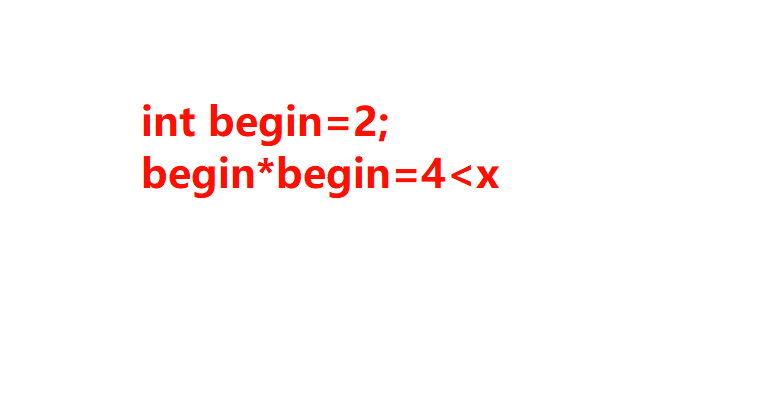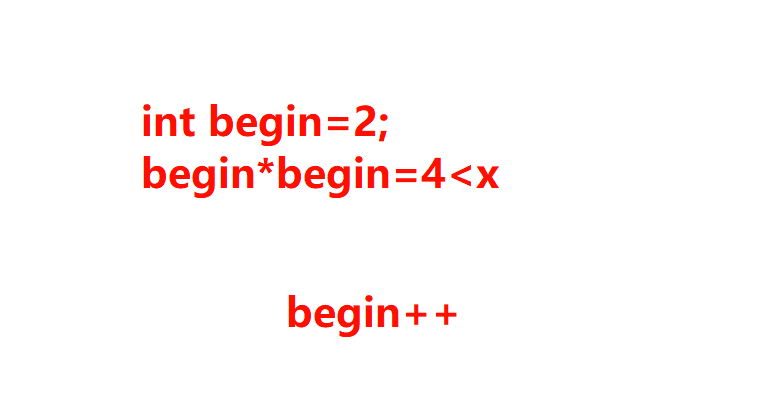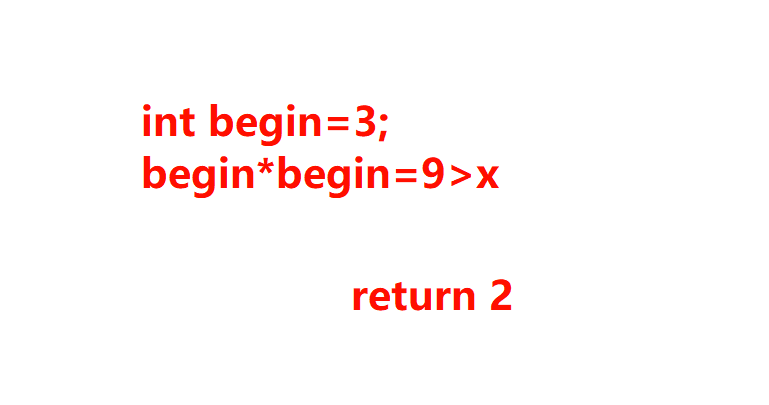在之前的学习当中我们已经初步了解过了二分查找的整体逻辑以及二分查找,接下来我们在本篇当中将系统的来学习二分查找的使用方式以及在什么情况下可以使用二分查找。在之前的学习当中我们了解到的二分查找是要求在有序的数组当中当数组元素有序时才能使用,但是其实这只是二分查找最朴素的使用场景,接下来我们将学习更多的二分查找的使用场景。相信通过被本章的学习之后你会有所收获,一起加油吧!!!
1.二分查找算法
在之前我们就已经初步了解过了二分查找算法,在此二分查找的本质就是将原来的数组来进行不断的折半直到找到要查找的元素为止,因此二分查找也叫作折半查找。那么接下来我们就先来通过以下的算法题来巩固之前学习过的最为朴素的二分查找
1.2 朴素二分查找
通过以上的题目描述就可以看出该算法题要我们实现的是在给定的升序数组当中找出指定值target的数组下标,如果找不到就返回-1.
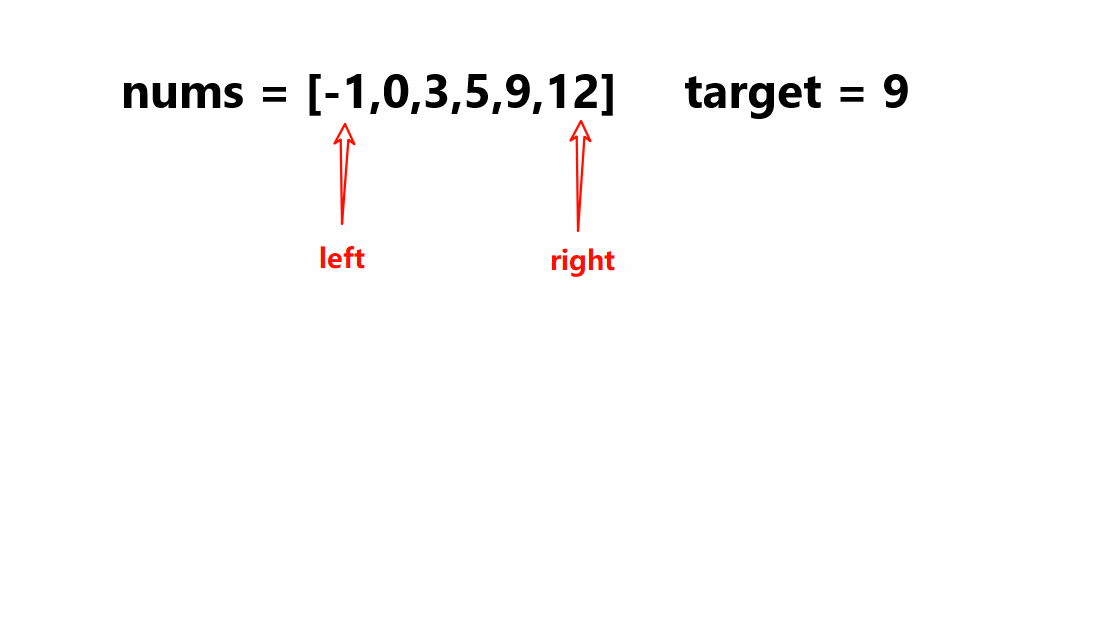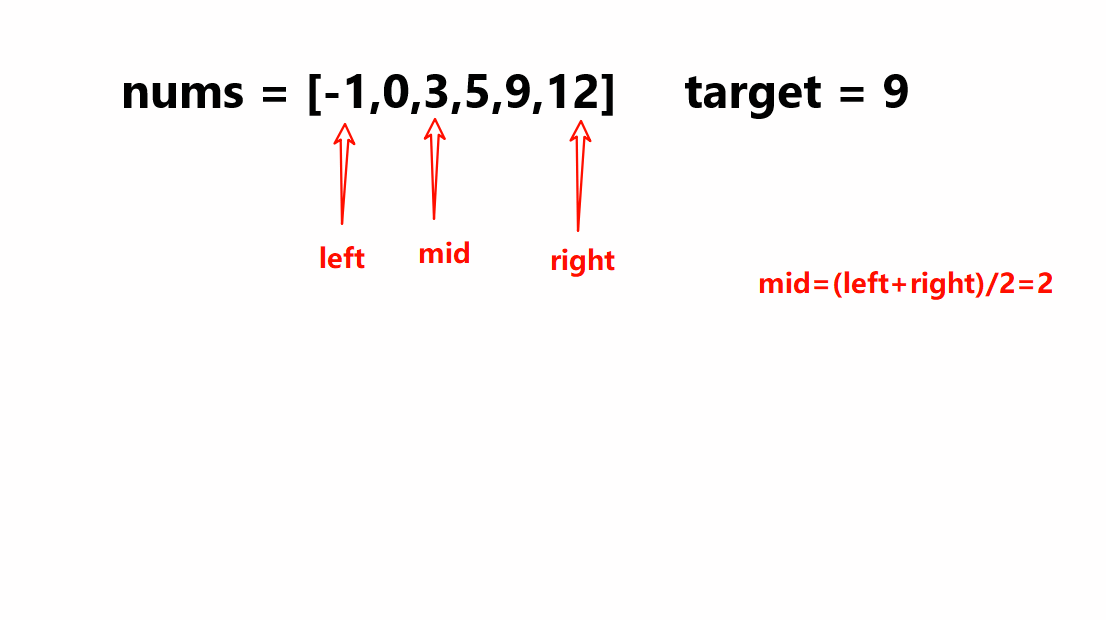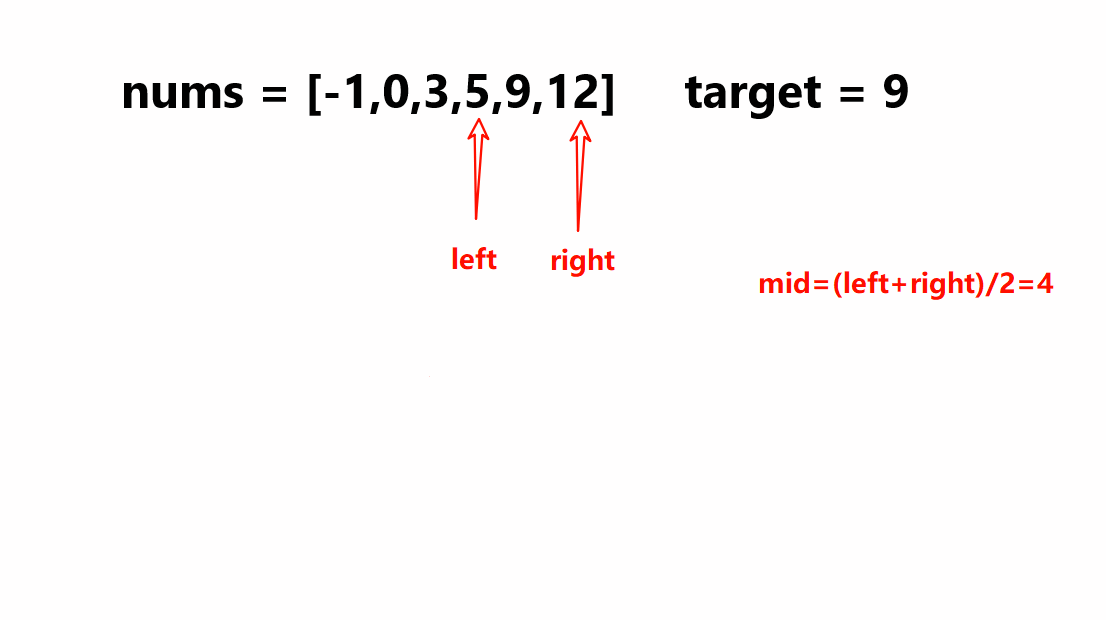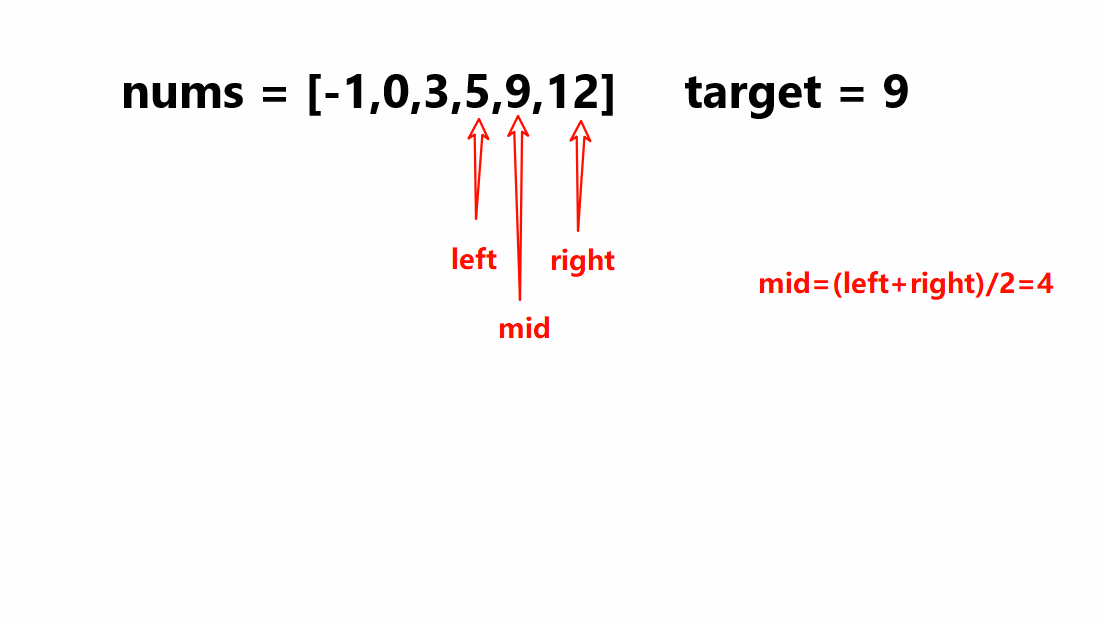
那么此时在升序数组当中要进行查找就可以使用到二分查找,这时一开始创建两个变量left和right分别指向数组当中首元素和最后一个元素的下标,之后创建变量mid指向left下标和right下标之间的中间值,再比较nums[mid]和指定值target的大小;若nums[mid]比target大就说明此时target是落到left到mid-1的区间内,这时就需要将right移动到mid-1的位置;若nums[mid]比target小就说明此时target是落到mid+1到right的区间内,这时就需要将left移动到mid+1的位置;若nums[mid]的值等于target就说明此数组当中值为targert的元素下标为mid。在此是一直循环以上操作直到left大于right就停止。
例如以上示例1当中过程就如下所示:
接下来我们就可以来实现以上算法题,代码如下所示:
class Solution {
public:
int search(vector<int>& nums, int target)
{
int left=0,right=nums.size()-1;
while(left<=right)
{
//找到left和right中间元素的数组下标
int mid=(right+left)/2;
//如果target比下标mid对应的数组元素小就将left到right区间缩小为left到mid-1
if(nums[mid]>target)right=mid-1;
//如果target比下标mid对应的数组元素大就将left到right区间缩小为mid+1到right
else if(nums[mid]<target)left=mid+1;
//当target和下标mid对应的数组元素一样大时就说明在数组当中找到值为target的元素这时就返回mid
else return mid;
}
//最终为找到就返回-1
return -1;
}
};注:在以上算法题当中题目的数组长度较短,在计算mid时不会出现超出int的数据范围的情况,但有时数组的长度较长时使用mid=(right-left)/2就会出现超出数据范围的问题,那么这时就可以使用mid=left+(right-left)/2或者是mid=left+(right-left+1)/2,在此只是在个数是偶数时有所差别,使用这两种就不会出现超出数据范围的问题了
以上就是该算法题的整个解决流程了,相信通过这道算法题你应该回忆起来了之前我们学习过的二分查找算法,那么接下来我们就来二分查找当中除了朴素二分查找之外的另外两个二分查找的模板,分别是查找左边界的二分查找模板和查找右边界的二分查找模板。
1.2 查找左右边界的二分查找
注:在此切记在了解以上以上所述的两种模板过程中不要死记硬背,要理解之后再记忆,否则二分查找就会是最容易写出死循环的算法
接下来就通过一道算法题来了查找区间的左端点和查找区间右端端点的二分查找模板
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
通过以上的题目描述就可以看出该算法题要我们实现的是在给定的非递减数组当中找出元素值为target的子数组区间,如果原数组当中不存在值为target的值就返回区间[-1,-1]
并且在这道算法题当中题目要求我们要设计出时间复杂度为O(log n)的算法,那么这就使得我们无法使用从头暴力遍历数组的方式来实现查找。这时你可能就想到使用二分查找来解决,但是在之前使用二分查找当中数组都是单调递增的,并且在之前使用二分查找都是查找指定的元素,而现在需要查找的是一个区间;这就使得就算使用朴素的二分查找找到指定值区间内的值最后找区间的时间复杂度也无法达到O(long n)。因此要解决这道题就不能再使用朴素版本的二分查找,而是使用查找左区间和右区间的二分查找。
其实以上两个改进的二分查找也是基于朴素的二分查找实现的,只不过在查找时改变了查找的策略。在此使用二分查找就只需要给定的数据具有二段即可
接下来就通过以上题目当中的示例1来了解具体过程该如何实现
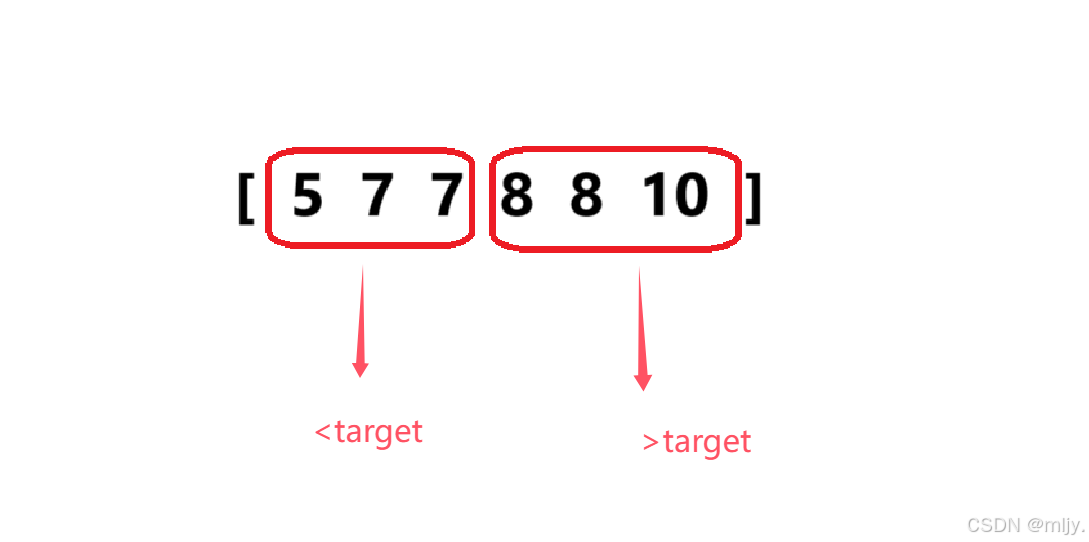
在此可以将原数组划分为两部分分别是元素值小于target的部分和元素值大于targe的部分
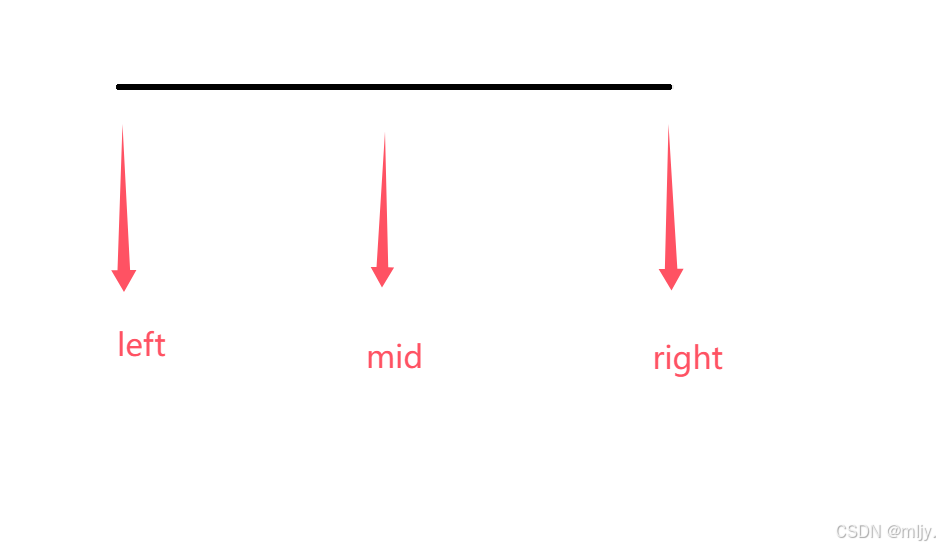
在此在查找区间的左端点时还是先通过求出left和right之间的中间值下标mid
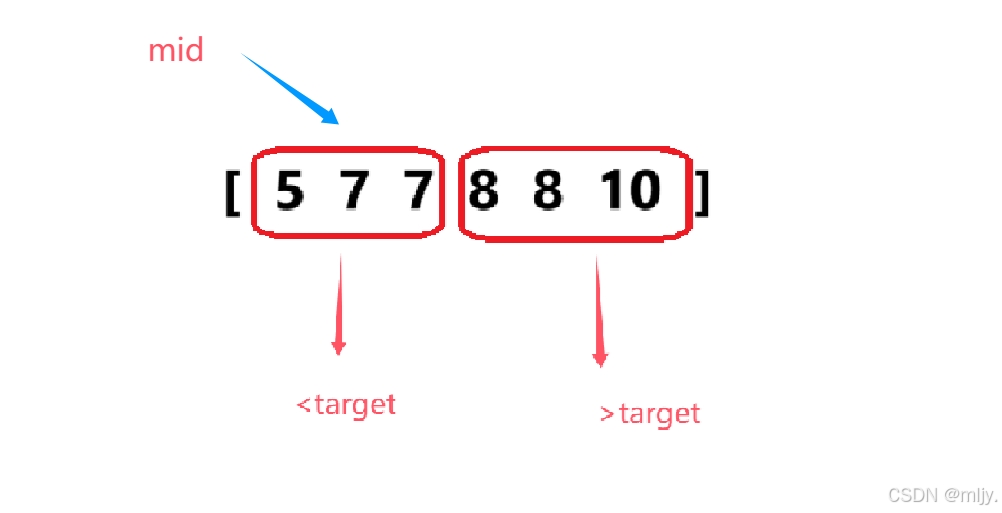
首先来看查找左端点时:
此时如果nums[mid]的值是小于target的,这就说明此时的mid落在元素值<target的区间内
由于最后我们是要找出值为target的区间,因此最后区间内的所有元素值都是等于target的,那么nums[mid]落在元素值小于target的区间就说明从left到mid的值都是小于target的;都不满足要求这时就可以将left移动到mid之后一位,也就是将left=mid+1
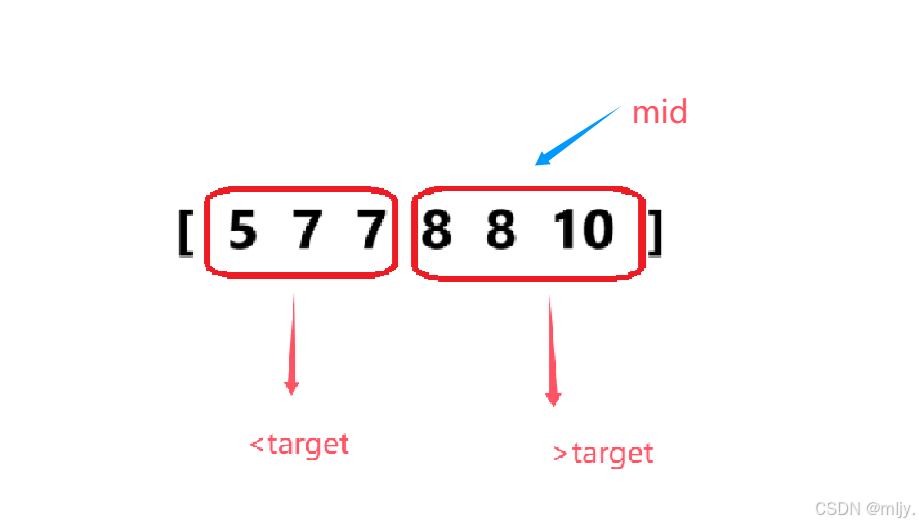
接下来来看查找右端点:
此时如果nums[mid]的值是大于target的,这就说明此时的mid落在元素值>target的区间内
由于最后我们是要找出值为target的区间,因此最后区间内的所有元素值都是等于target的,那么nums[mid]落在元素值大于target的区间就说明此时mid位置的值有可能满足要求的,所以这时就可以将right移动到mid的位置;也就是right=mid
在以上我们已经将使用二分查找区间的左端点和右端点的大致过程给描述亲清楚了,但是其实在此我们还有两个很重要的细节问题要来处理;分别是在寻找左右端点的过程当中循环的结束条件以及求中间节点的操作
首先在循环条件在之前朴素二分查找当中是left<right,那么是不是在查找左、右区间时也是这样的呢?接下来就来具体分析看看
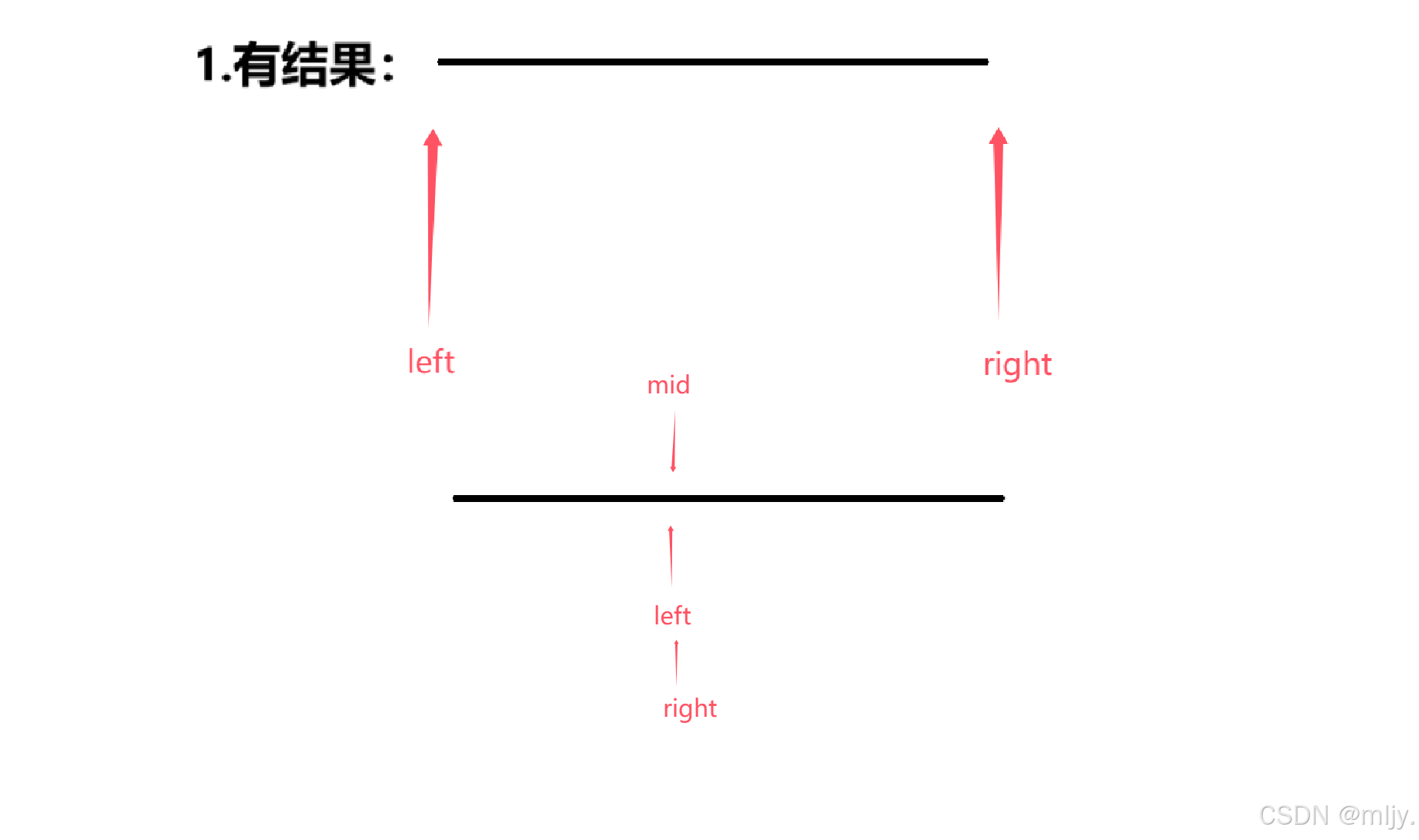
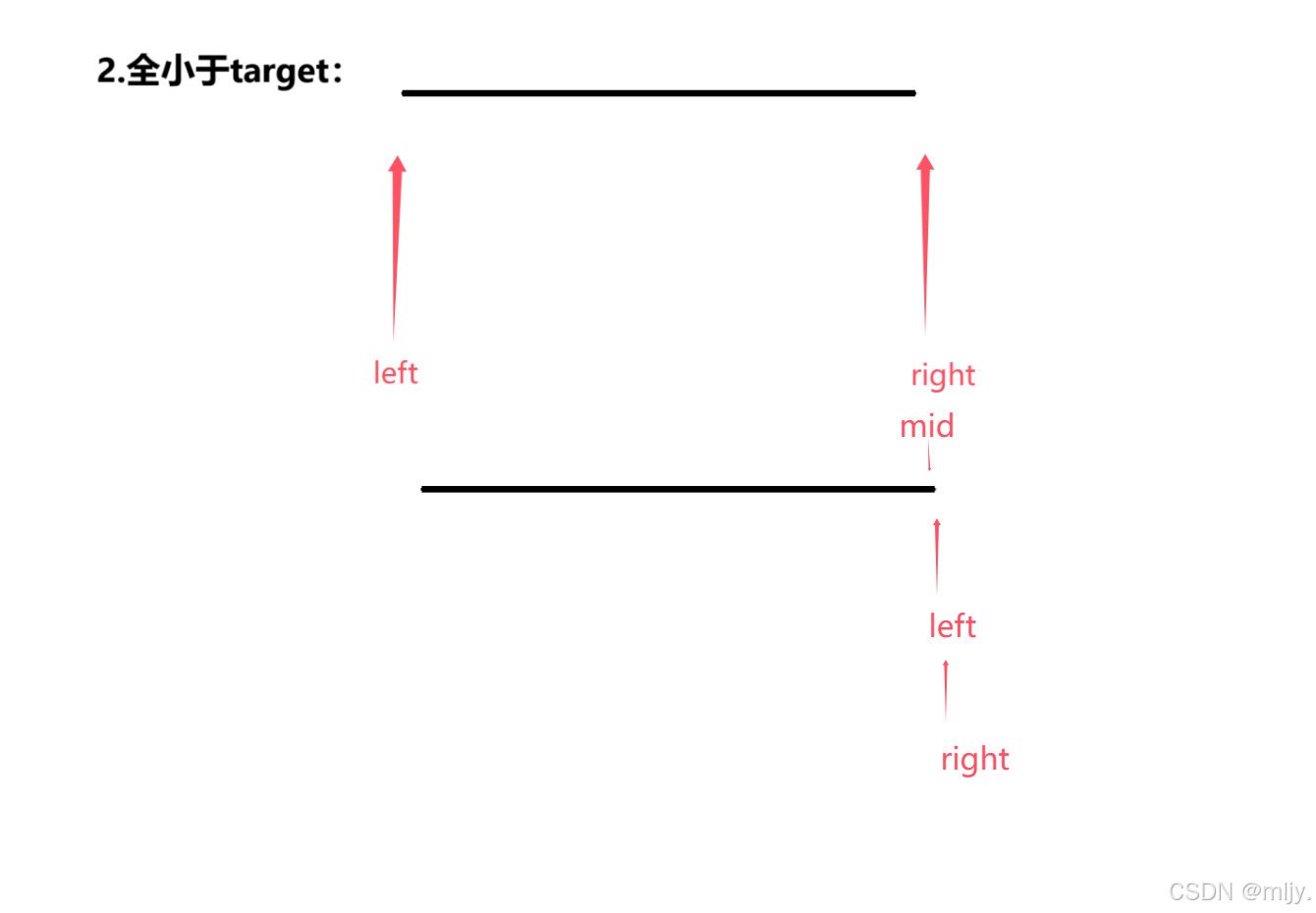
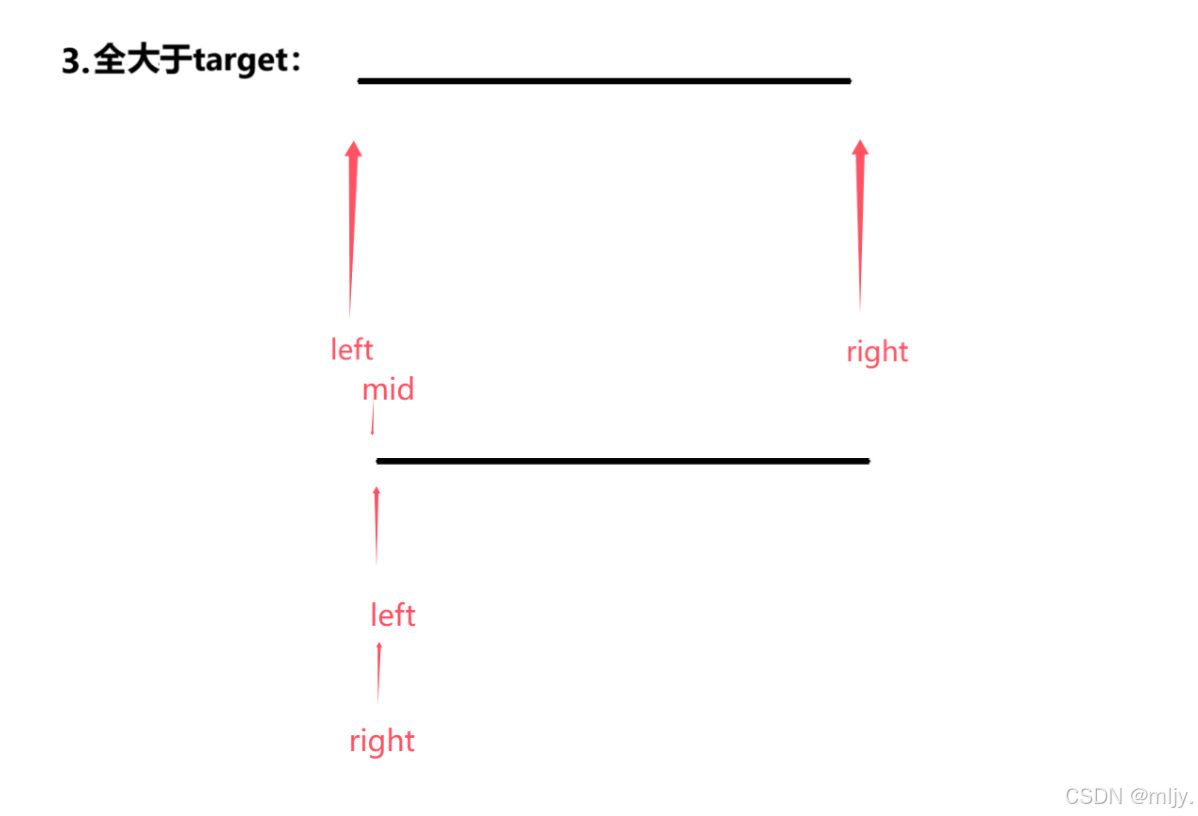
我们知道在查找左区间的端点时会有能找到端点在left和right之间,还有给定的数据值都是小于target的,最后一种是给定的数据全部都是大于target的
在这以上三种情况当中都是当left都等于right就不需要再进行判断了,并且在情况一和情况三当中如果将循环条件定为left<=right,由于进行的操作是right=mid,这时就会出现死循环
因此综上所述寻找区间左端点时的循环结束条件要定为left<right
原因有两点:1.left=right时,此时left或者right指向的下标就是结果,无需判断
2.若进行left=right的判断就会在一些场景下出现死循环
寻找右区间的端点的循环条件的分析于以上左端点类似在此就不再进行细致的分析,右端点时的循环结束条件也要定为left<right
分析了循环的条件之后接下来我们接着来分析寻找左、右端点时中间节点的选取有什么限制吗?
在选择中间节点计算有两种分别是mid=left+(right-left)/2和mid=right+(right-left+1)/2,在此这两种只是在数据个数是偶数时有区别
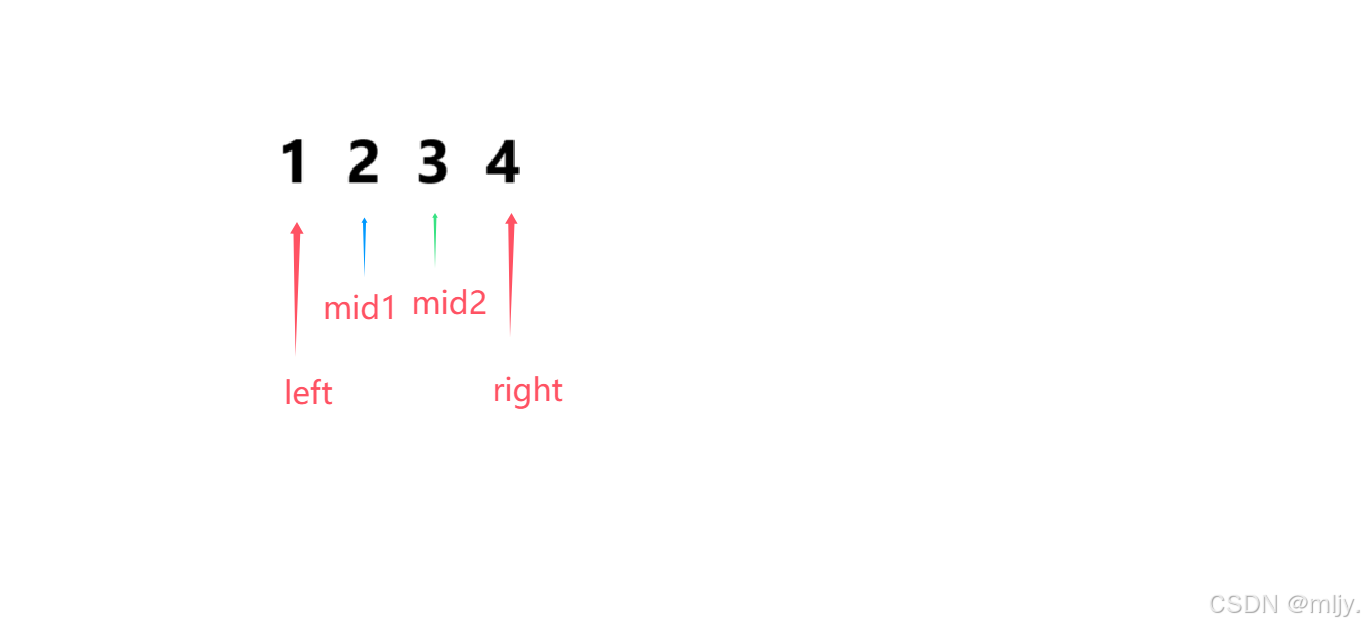
例如以下示例
mid1就是使用 left+(right-left)/2求出的,mid2就是使用right+(right-left+1)/2求出的
先来分析左端点:
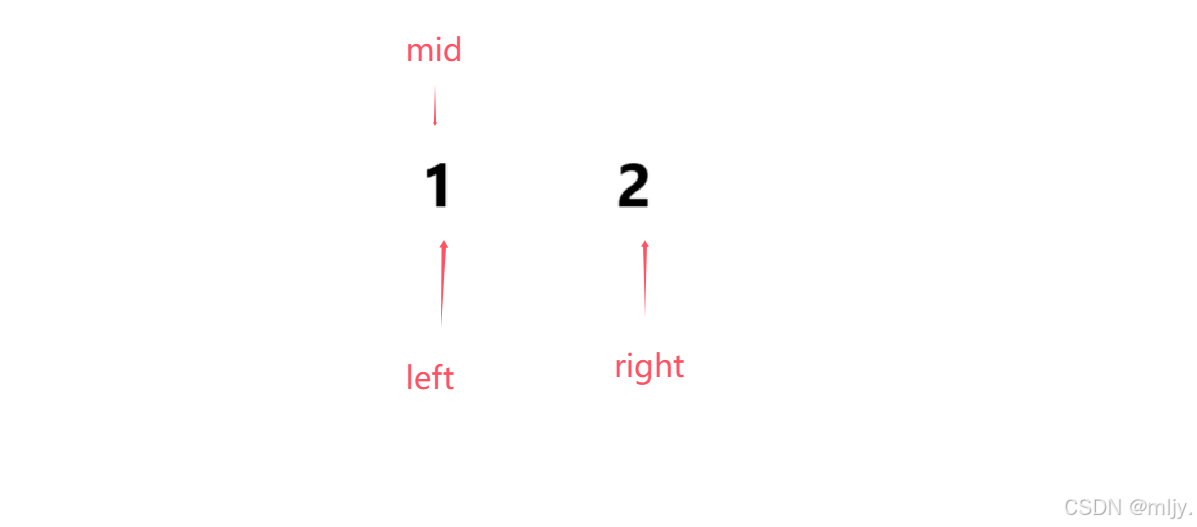
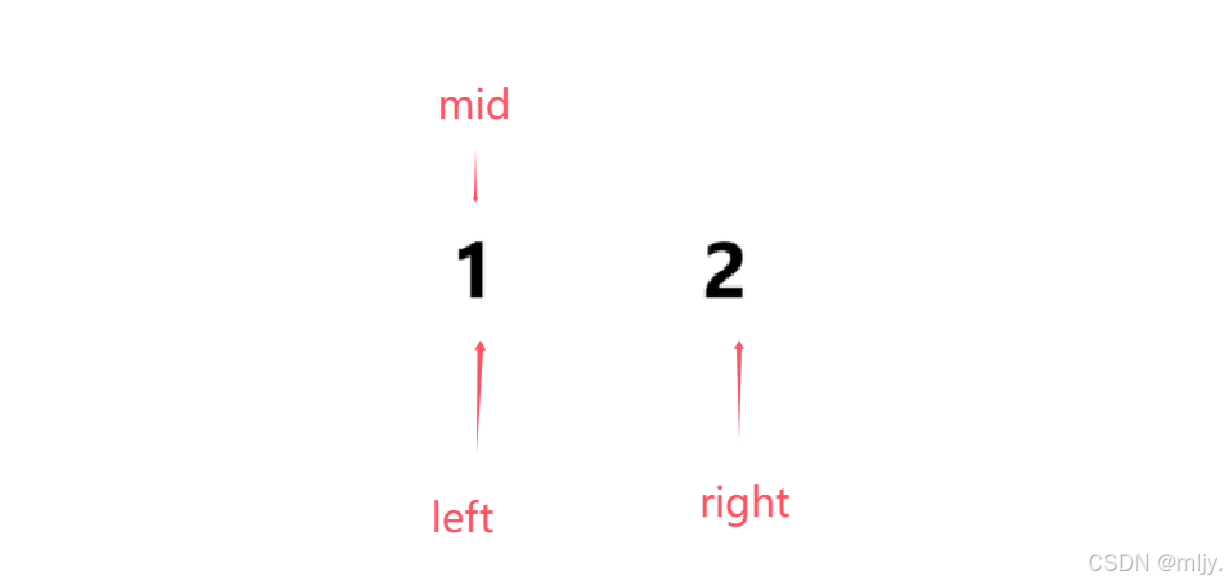
在寻找区间的左端点时如果只有两个数据时如果第二个数据值是等于target的,那么来依次分析使用mid=left+(right-left)/2和mid=right+(right-left+1)/2是否都符合要求
这时如果是使用 mid=left+(right-left)/2就可以得出mid指向1,那么再进入循环就会将left移动到mid+1也就是right的位置,此时之后left=right,最终是符合要求的
这时如果是使用 mid=left+(right-left+1)/2就可以得出mid指向2,那么再进入循环就会一直让right=mid,此时就会造成死循环,最终是不符合要求的
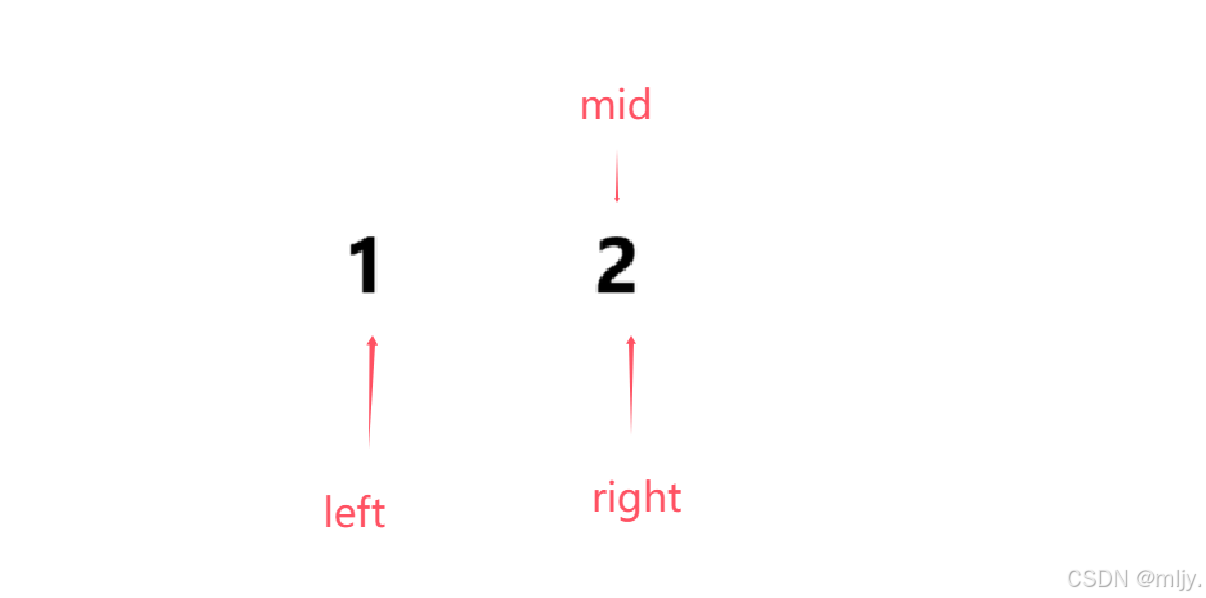
因此综上就可以得出在求区间的左端点时中间下标要使用 mid=left+(right-left)/2
接下来分析右端点:
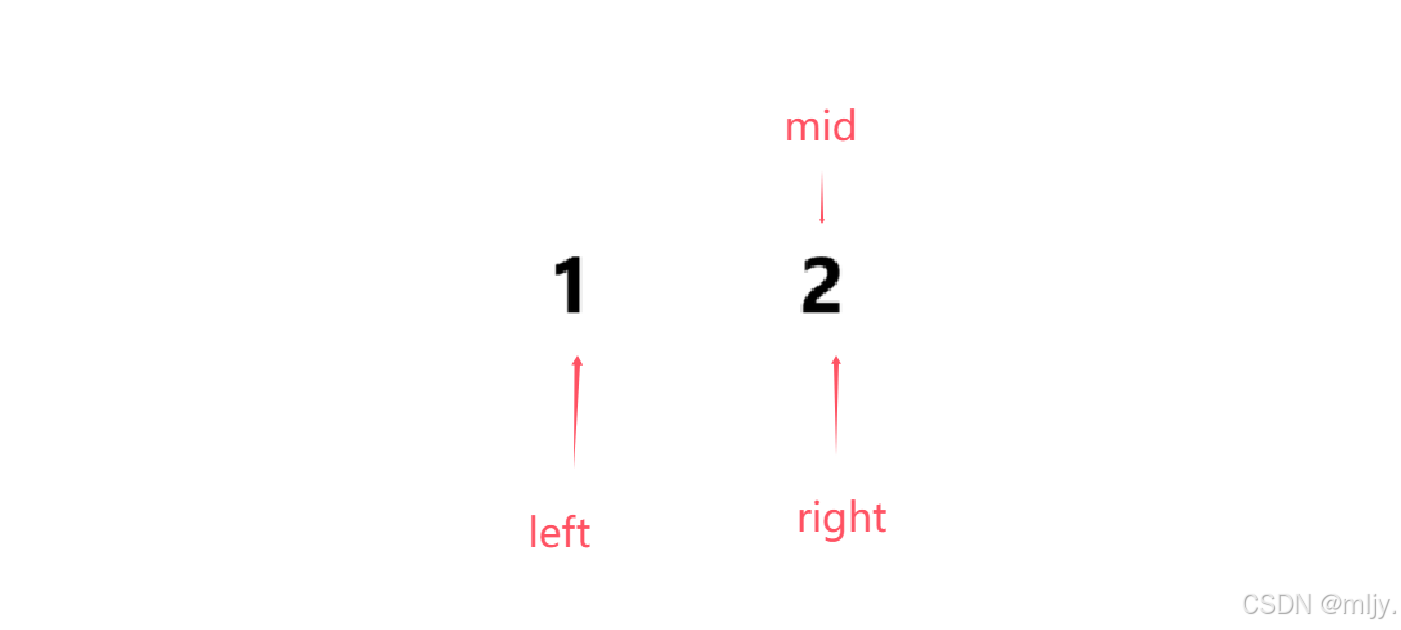
在寻找区间的右端点时如果只有两个数据时如果第一个数据值是等于target的,那么来依次分析使用mid=left+(right-left)/2和mid=right+(right-left+1)/2是否都符合要求
这时如果是使用 mid=left+(right-left)/2就可以得出mid指向1,那么再进入循环就会一直让left=mid,此时就会造成死循环,最终是不符合要求的
这时如果是使用 mid=left+(right-left+1)/2就可以得出mid指向2,那么再进入循环就会将right移动到mid-1也就是left的位置,此时之后left=right,最终是符合要求的
因此综上就可以得出在求区间的右端点时中间下标要使用 mid=left+(right-left+1)/2
完成以上两个细节的分析接下来我们就来试着实现该算法题的代码:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target)
{
//若nums的长度为0就说明数组内不可能找到目标值,直接返回[-1, -1]
if(nums.size()==0)return {-1,-1};
//查找区间左端点
int left=0,right=nums.size()-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<target)left=mid+1;
else right=mid;
}
//将左端点值用begin标记
int begin=left;
//查找区间右端点
left=0,right=nums.size()-1;
while(left<right)
{
int mid=left+(right-left+1)/2;
if(nums[mid]>target)right=mid-1;
else left=mid;
}
//将右端点值用end标记
int end=left;
//判断begin指向的元素是否和目标值相等
//是的话就说明存在目标值,否则就不存在
if(nums[begin]!=target)return {-1,-1};
else return {begin,end};
}
};那么通过以上的算法题就可以得出查找区间左端点和查找区间右端点的模板
总结模板
将以上的 · 查找区间左和右端点的步骤总结就可以得出以下的模板
在此切记不要死记模板,大家一定不要觉得背下模板就能解决所有⼆分问题。二分问题最重要的就是要分析题意,然后确定要搜索的区间,根据分析问题来写出⼆分查找算法的代码。
在此你只要记住的是当if……else语句当中出现mid-1时就要将确定中间下标mid写成mid=left+(right-left+1)/2。
2.二分查找算法题练习
接下来在我们就会通过几道算法题来巩固之前学习的二分查找算法,并且每道题都会以题目解析、算法原理讲解、代码实现三步带你完全理解每道算法题
2.1 搜索插入位置
题目解析
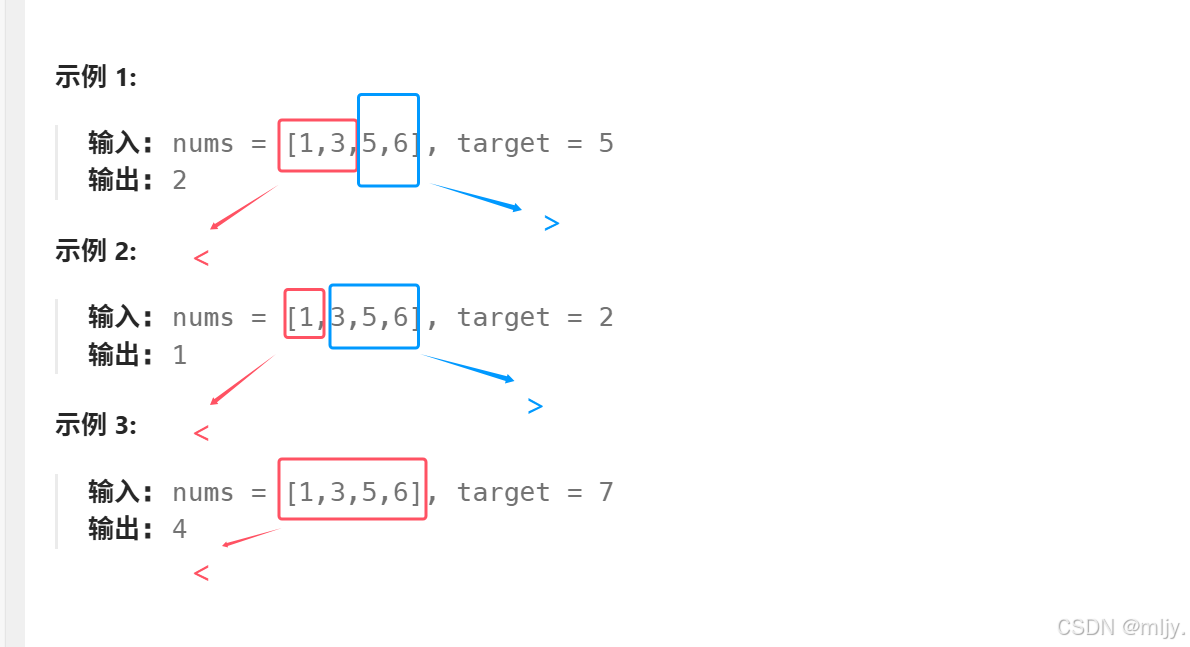
通过以上的题目描述就可以看出该算法题要我们实现的是在找到目标值为target的元素下标,并且当在数组当中找不到对应元素时就要找出该值插入到数组当中使数组依然保持升序的数组下标
算法原理讲解
在该算法题当中要求我们使用O(long n)的算法效率来实现,那么这就使得我们不能使用暴力遍历数组来实现,那么我们就要试着使用其他的方式来实现了
在这道题当中其实我们是可以将数组分为两个部分的,一部分是小于给定值target的,另一部分是大于指定值target的部分,就例如以上的示例
那么这时就说明给定的数组是拥有二断性的,这时就可以使用二分查找算法来实现实现,这时当数组当中存在指定值target时就最终查找完毕就返回的是值为target元素的下标,如果数组当中不存在值为target的值最终就返回的是比target值大的元素的值,这时恰巧就是之后要将值为target的元素插入的位置。
那么以上的情况我们使用一个查找左区间的二分查找就可以实现了,但有一种特殊情况需要我们单独处理一下,那就是当数组当中不存在值为target的值 ,并且若要插入target的值最终是插到数组的末尾,这时二分查找的结果是数组的最后一个元素的下标就不符合要求。这时这种情况的特点其实就是target>nums[left],那么就只需要在二分查找之后进行判断如果满足条件就返回left+1的值
代码实现
class Solution {
public:
int searchInsert(vector<int>& nums, int target)
{
int left=0,right=nums.size()-1;
//查找区间左端点
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]<target)left=mid+1;
else right=mid;
}
//如果target的值大于nums[left]位置的值就说明target要插入的位置是数组的尾部
if(target>nums[left])return left+1;
return left;
}
};2.2 x 的平方根
题目解析
在这道算法题当中题目给定了我们一个非负整数x,在此我们需要找出这个整数的算数平方根,如果得到的平方根是不是整数就只需要将整数部分返回,小数部分去掉
算法原理讲解
在这道题当中题目要求我们不能使用内置指数函数pow,sqrt等,那么这时我们就要想着如何使用其他的方式来实现了。
在此最容易想到的方法就是从1开始到x判断对应的数平方是不是等于x,是的话就返回此时的值,如果出现此时的平方值大于x就返回此时的值减一的值。并且在这些步骤的最开始就判断x的值是否是等于0,是的话就直接返回0
例如以上的示例2
要从1到8依次查找,过程图如下所示:
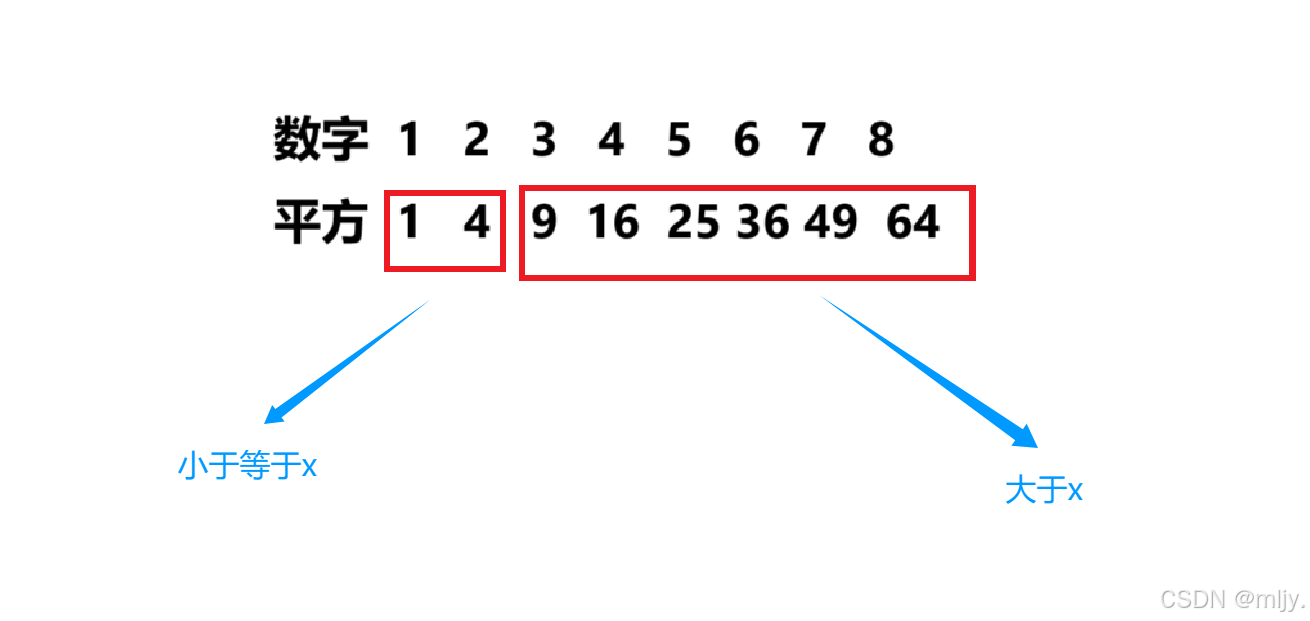
那么除了以上的解法还有什么更好的算法呢,在此从1到x的数字的平方其实可以分为两个部分,就是平方值小于等于x的值和平方值大于x的值
例如以上的示例2:
那么这时我们不就是要查找右区间吗?
因此这时就可以使用查找右区间的二分查找算法来实现,创建两个变量left和right分别初始化为1和x,创建mid变量存储中间值下标,之后当mid平方大于x时就将right移到mid的位置,当mid平方的值小于等于x的值就将left移动到mid-1的位置,最后重复以上的操作最后left或者right的值就是要返回的值
代码实现
暴力查找代码:
class Solution {
public:
int mySqrt(int x)
{
if(x==0)return 0;
//反正数据溢出要将begin类型定为long long
long long begin=1,end=x;
while(begin<=end)
{
if(begin*begin==x)
{
return begin;
}
else if(begin*begin>x)
{
return begin-1;
}
begin++;
}
//保证每个函数路径都有返回值
return -1;
}
};二分查找版本代码:
class Solution {
public:
int mySqrt(int x)
{
if(x==0)return 0;
int left=1,right=x;
while(left<right)
{
//因为x最大值为int的最大值,mid类型创建为long long防止溢出
long long mid=left+(right-left+1)/2;
//当当前的mid平方大于x的值时
if( (mid*mid)>x)right=mid-1;
//当当前的mid平方小于x的值时
else left=mid;
}
return left;
}
};
2.3 山峰数组的峰顶

题目解析
通过以上的题目描述就可以看出该算法题要我们实现的是从数组当中找出峰值元素,也就该元素比其左边的元素大,比其右边的元素小,并且题目给定的数组长度最小为3,保证会有峰值元素
算法原理讲解
在此题目要求我们实现出时间复杂度为O(log n)的算法,那么这就使得我们不能使用遍历数组来实现,那么要求O(log n)的算法,那就试着看能不能使用二分查找来实现,这时就要看数组当中是否具有二段性
在此是可以看出给定的数组是具有二段性的,数组的左半部分的元素前面的元素值都小于后面元素的值;数组的右半部分的元素前面的元素的值都大于后面的元素值。
例如以上示例:
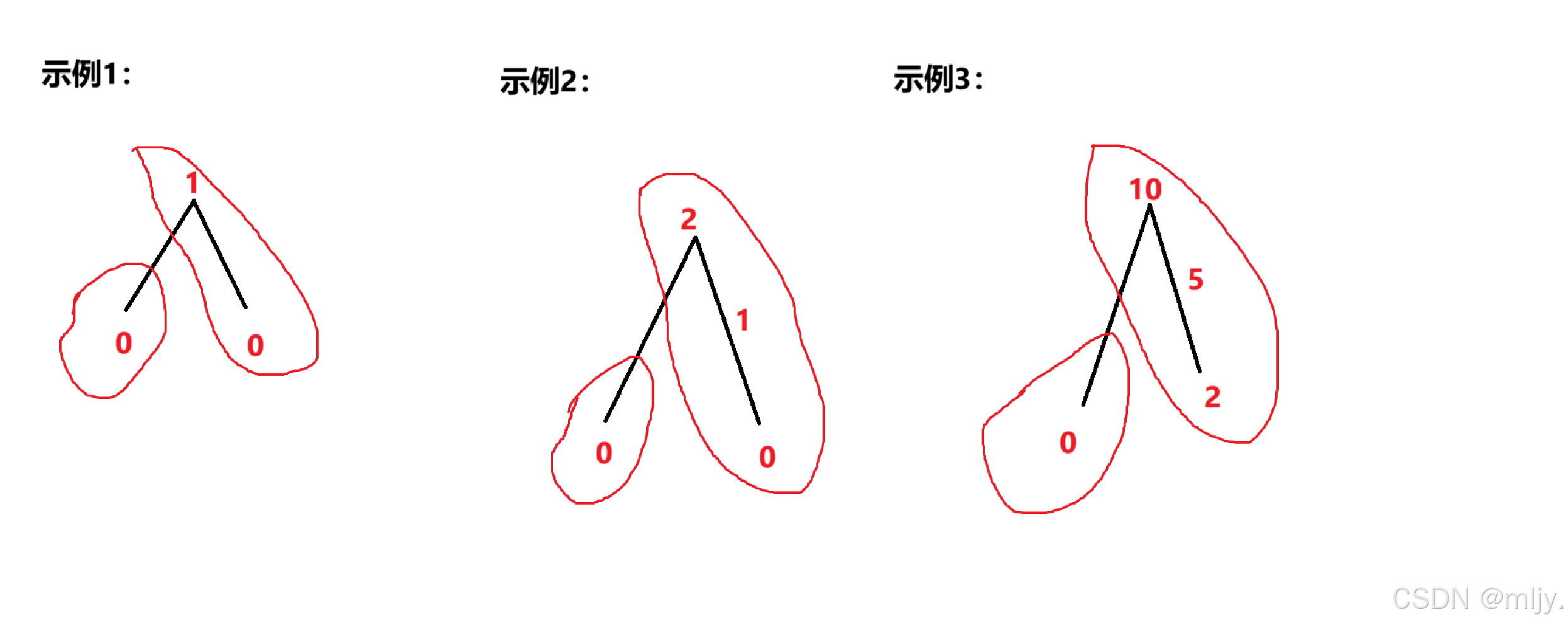
因此要实现这道算法题其实只需在在数组当中查找左边元素大于右边元素的左区间,这时最终循环结束的适合left指向的下标就是我们想要的值
代码实现
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr)
{
int left=0,right=arr.size()-1;
while(left<right)
{
//得到中点值的下标
int mid=left+(right-left)/2;
//当左边元素的值小于右边元素的值时
if(arr[mid]<arr[mid+1])left=mid+1;
//当左边元素的值大于右边元素时
else right=mid;
}
return left;
}
};2.4 寻找峰值

题目解析
通过以上的题目描述就可以看出该算法题要我们从给点的数组当中找出峰值元素的下标,在数组当中有可能有多个元素都是峰值元素;那么这时我们只需要找出一个符合要求的峰值元素下标即可。并且题目中还规定nums[-1]=0,nums[n]=-∞,这就可以使得数组即使是只有一个元素时也是有峰值的。
算法原理讲解
在以上算法题当中要求使用O(long n)效率的时间复杂度解决,那么这时我们就要看看给定的数组是否有二段性,有的话就可以试着使用二分查找算法来解决
由于给定的数组时有多个峰值元素的,因此在该数组当中我们就可以将其划分为两个区间;分别是左元素值大于右元素值得区间,和左元素值小于右元素值得区间,这时就说明数组是有二段性的。
例如以上示例:

代码实现
class Solution {
public:
int findPeakElement(vector<int>& nums)
{
//当数组长度为0时,下标为0位置的元素就是峰值元素
if(nums.size()==1)return 0;
int left=0,right=nums.size()-1;
while(left<right)
{
//得到中间值的下标
int mid=left+(right-left)/2;
//当左边的元素值小于右边的元素值就将left移动到mid+1的位置
if(nums[mid]<nums[mid+1])left=mid+1;
//当左边的元素值大于右边的元素值就将right移动到mid的位置
else right=mid;
}
return left;
}
};2.5 搜索旋转排序数组中的最小值
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)

题目解析
通过以上的题目描述就可以看出该算法题要我们实现的是在更定的经过多次旋转之后是升序的数组当中找出值最小的元素。
算法原理讲解
在此你看到这道算法题的第一想法就是将给定的数组旋转之后变回升序这样数组的第一个元素就是最小的元素,但是题目要求用O(long n)的时间复杂度来解决,以上这种算法当数组一开始是逆序的适时候时间复杂度为O(n),这就不符合我们的要求了,因此我们要再想想其他的算法。
在此我们来观察数组是否有二段性,因此来判断是否能使用二分查找
在此如果数组不是一开始就是升序情况时,是可以将数组划分为以下两个区间的,两个区间内的数组元素都是升序的
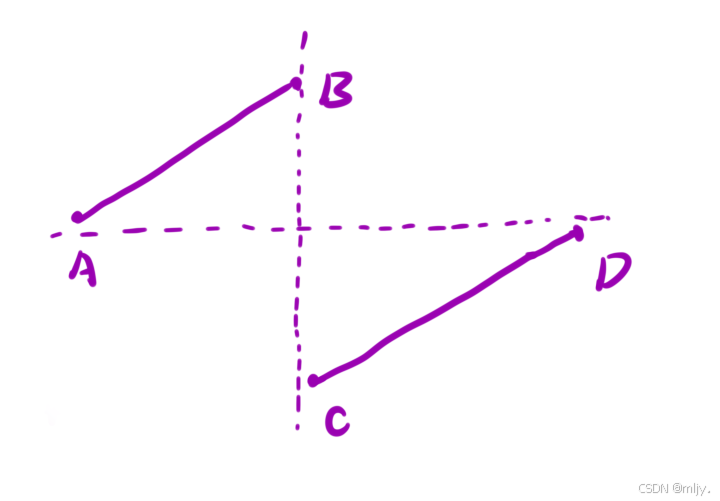
通过图像我们可以发现, [A,B] 区间内的点都是严格大于 D 点的值的, C 点的值是严格小于 D 点的值的。但是当 [C,D] 区间只有⼀个元素的时候, C 点的值是可能等于 D 点的值的。
因此一以上就根据元素的值是否大于数组最后一个元素的值将其划分为两个区间,这样数组就具有二段性,就可以使用二分查找算法
例如以上题目的示例:
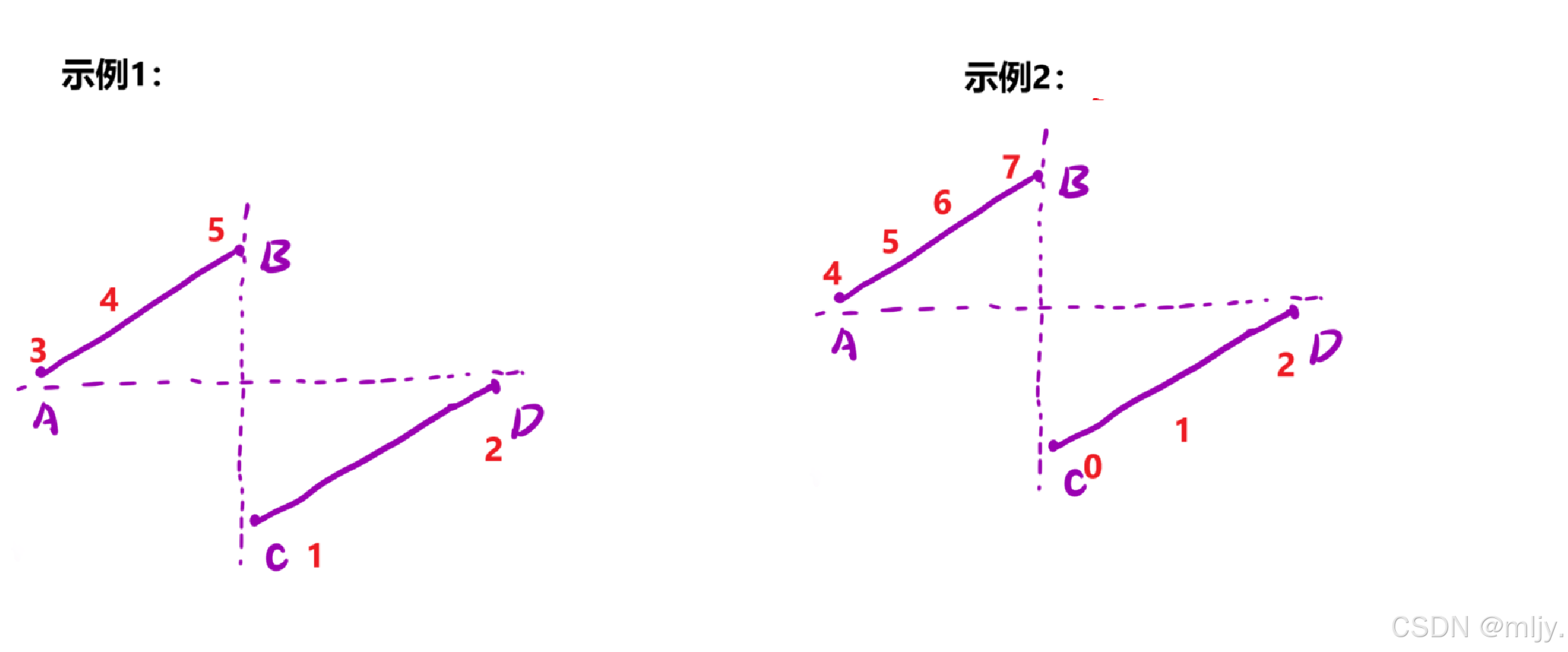
那么就可以使用查找左端点的二分查找算法来实现,一开始就判断数组当中的最后一个元素是否大于数组的首元素,是的话就说明数组已经有序就直接返回数组的首元素即可。初始化两个变量left和right;两个变量分别初始化为0和nums.size()-1,之后创建表示中间值下标的变量mid,之后进行判断当nums[mid]>数组最后一个元素时就将left移动到mid+1的位置否则就将right移动到mid的位置。一直重复以上操作直到left等于right此时left下标指向的数组元素就是数组当中的最小值。
代码实现
class Solution {
public:
int findMin(vector<int>& nums)
{
int n=nums.size();
//当数组为升序时直接返回
if(nums[0]<nums[n-1])return nums[0];
int left=0,right=n-1;
//查找左端点
while(left<right)
{
int mid=left+(right-left)/2;
if(nums[mid]>nums[n-1])left=mid+1;
else right=mid;
}
return nums[left];
}
};2.6 0〜n-1 中缺失的数字
题目解析
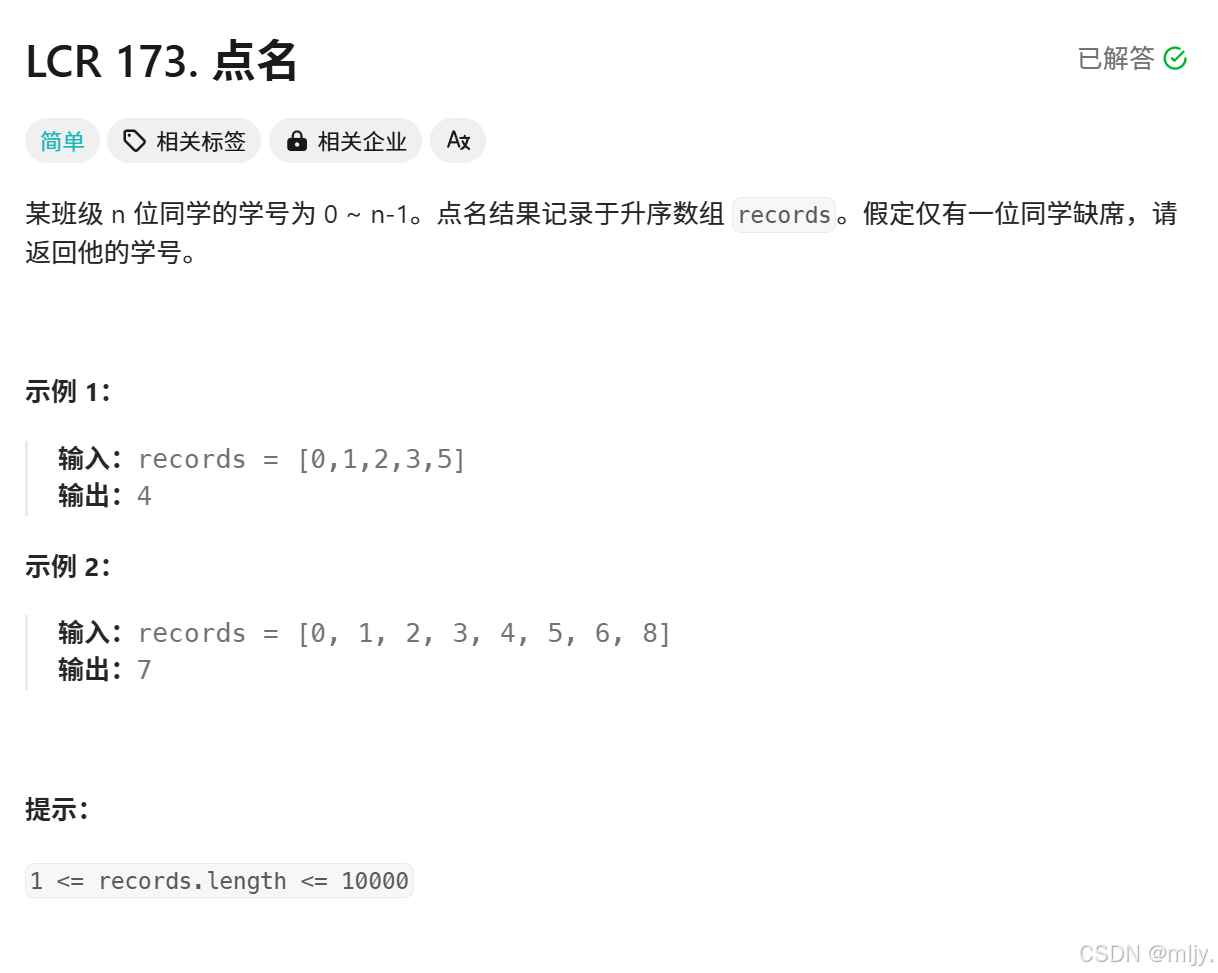
以上的题目的要求很简单;就是要从n个元素的数组当中找出0~n-1缺失的元素
算法原理讲解
在此算法题很简单就好想到的算法就是直接遍历数组,当数组下标和对应下标的元素不相等时就返回此时的下标,但这种算法的时间复杂度为O(n),还有什么更好的算法呢?
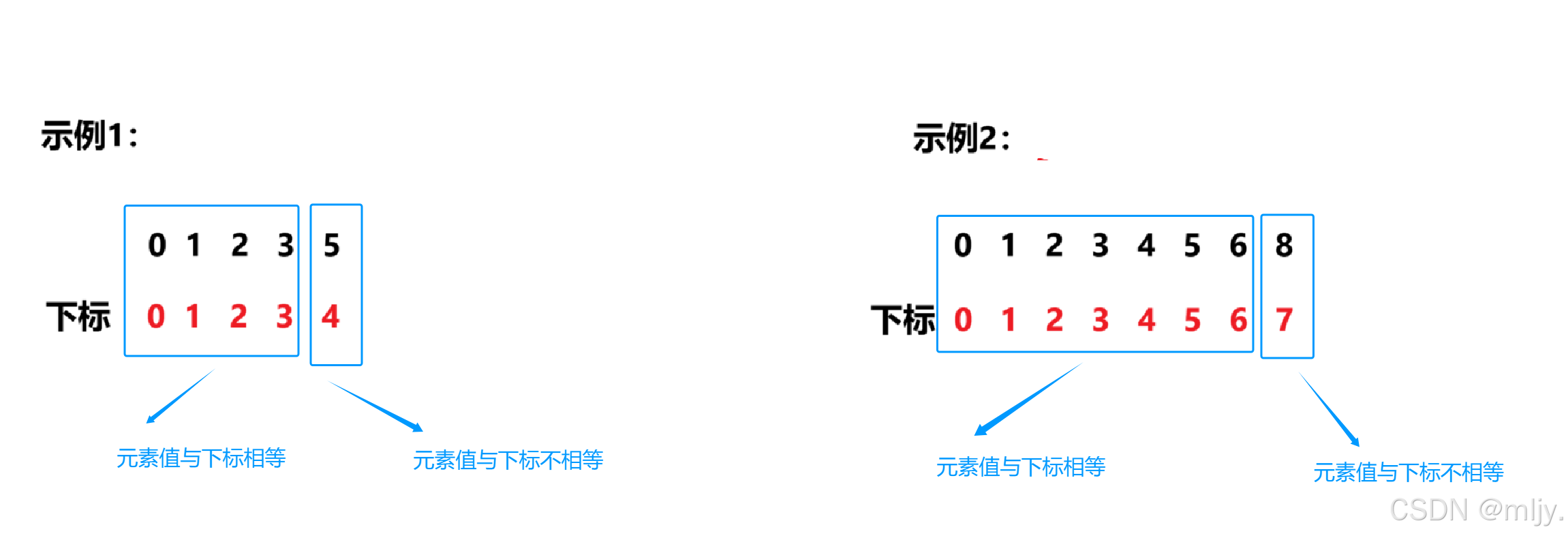
在此其实我们是可以根据数组元素的值是否与其下标相等将数组划分为两个区间
例如以上示例:
那么在此就可以使用查找左区间的二分查找算法来解决该算法题
代码实现
暴力查找法
class Solution {
public:
int takeAttendance(vector<int>& records)
{
for(int i=0;i<records.size();i++)
{
if(records[i]!=i)
return i;
}
return records.size();
}
};二分查找版本:
class Solution {
public:
int takeAttendance(vector<int>& records)
{
int left=0,right=records.size()-1;
while(left<right)
{
int mid=left+(right-left)/2;
if(records[mid]==mid)left=mid+1;
else right=mid;
}
//当数组的最后一个元素下标和元素值相等就说明缺少的元素下标为left+1
if(records[left]==left)left++;
return left;
}
};以上就是本篇的全部内容了,希望本篇的学习能让你对二分查找算法有更深的理解,接下来还会带来其他的优选算法,未完待续……