♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥
♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥
♥♥♥我们一起努力成为更好的自己~♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥
✨✨✨✨✨✨个人主页✨✨✨✨✨✨
在前面的博客C语言——有关排序的算法中,我们对一些排序算法有了一定的了解,接下来这一篇博客我们更加深入地了解不同的排序算法~
目录
排序的概念及应用
什么是排序呢?排序排序不就是排顺序嘛~确实是这样~
概念:排序就是使⼀串记录(数据)按照其中的某个或某些关键字的大小(某一种规律)递增或递减的排列起来的操作。 (也就是说我们按照规律可能排升序,也有可能排降序)
在我们的生活中,处处都有排序的影子~比如世界五百强,中国内地大学排名,学生成绩排名……这些都是排序的运用,程序员们就需要使用排序来解决问题~
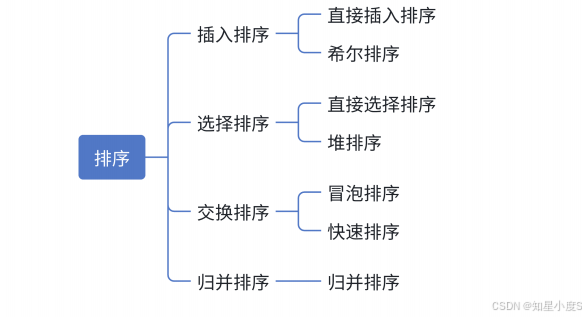
这里给出常见的排序算法~
有的排序算法(比如冒泡排序)在前面的博客中提到过~这一篇博客我们结合我们新学的知识进一步了解排序的算法~接下来,我们来一 一讲解这些不同的排序算法
插入排序
插入排序又可以分为直接插入排序和希尔排序,事实上希尔排序是直接插入排序的优化,接下来我们一个个来看~
直接插入排序
基本思想
基本思想:把待排序的记录 按其关键码值的大小逐个插入到⼀个已经排好序的有序序列 中,直到所有的记录插入完为止,得到⼀个新的有序序列 。
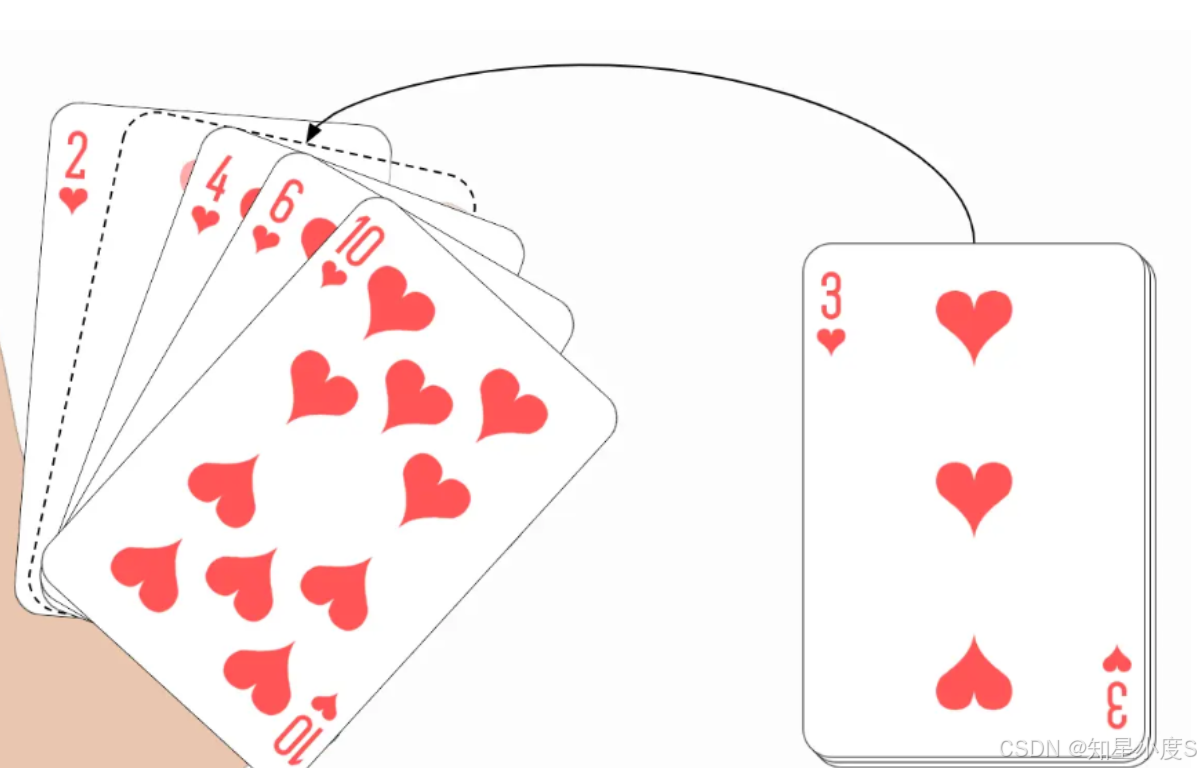
根据扑克牌的思想,首先我们循环拿到需要排序数组的每一个元素,使用end记录已经排序完成的数据最后一个下标,使用tmp保存需要排序的数据,end--往前面走,将tmp插入到前面排好的序列合适的位置。这里以升序为例,看看下面的代码~
代码
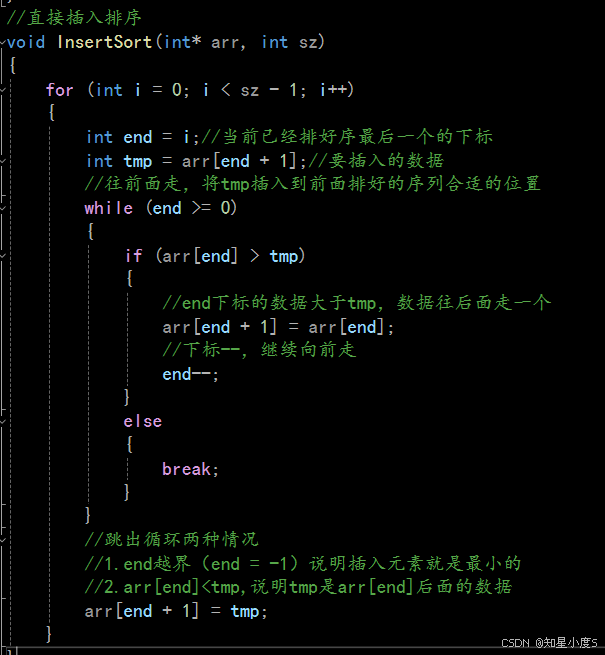
//直接插入排序
void InsertSort(int* arr, int sz)
{
for (int i = 0; i < sz - 1; i++)
{
int end = i;//当前已经排好序最后一个的下标
int tmp = arr[end + 1];//要插入的数据
//往前面走,将tmp插入到前面排好的序列合适的位置
while (end >= 0)
{
if (arr[end] > tmp)
{
//end下标的数据大于tmp,数据往后面走一个
arr[end + 1] = arr[end];
//下标--,继续向前走
end--;
}
else
{
break;
}
}
//跳出循环两种情况
//1.end越界(end = -1)说明插入元素就是最小的
//2.arr[end]<tmp,说明tmp是arr[end]后面的数据
arr[end + 1] = tmp;
}
}排序成功~
时间复杂度
接下来我们来看看,直接插入排序的时间复杂度应该怎么表示呢?
我们可以看到有两层循环,外层循环次数为n,内层循环次数当我们排序的数组是降序要排序成升序时,那么内层循环次数依次为1、 2、3……n,根据时间复杂度表示法的规则,取最坏的情况,那么时间复杂度就为O(N^2),不清楚的时间复杂度表示方法的记得看看这一篇博客哦~数据结构——复杂度
希尔排序
既然直接插入排序时间复杂度为O(N^2),那么有没有什么方法可以优化一下它呢?
接下来,就有我们的希尔排序来提高效率了~我们一起来看看~
基本思想
希尔排序法又称 缩小增量法 。希尔排序法的基本思想是:先 选定⼀个整数(我们一般选择是gap = n/3+1) ,把 待排序文件 所有记录分成各组 (所有的 距离相等的记录分在同⼀组内 ),并对 每⼀组内的记录进行排序 ,然后 gap=gap/3+1得到下⼀个整数,再将数组分成各组 ,进行插入排序,当gap=1时,就相当于 直接插入排序。前面gap>1时就是在进行预排序,把小的数据放在前面,大的数据放在后面~使数组接近有序~gap=1时,就是直接插入排序~
是不是看起来蒙蒙的,别急,我们画图来理解~
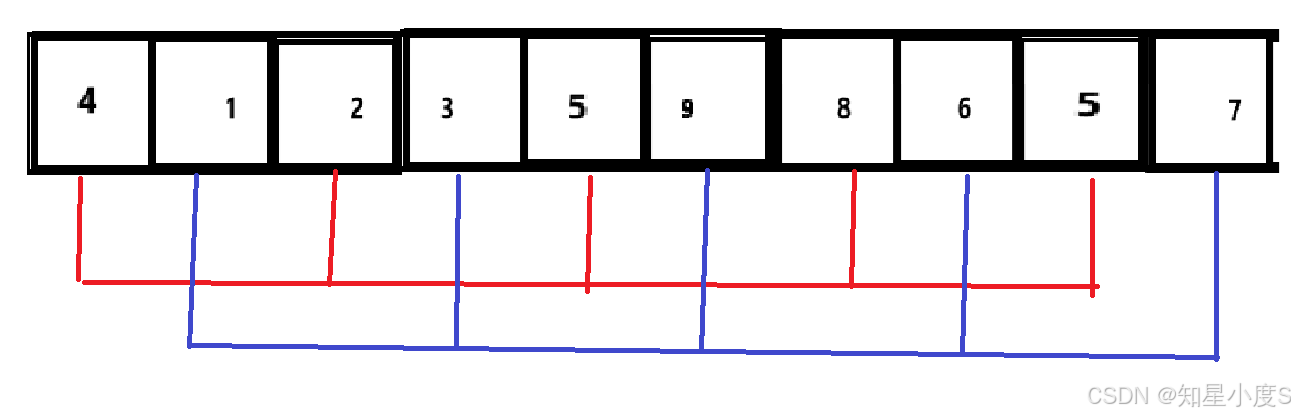
选择如果我们想要排序【9,1,2,5,7,4,8,6,3,5】这个数组,一共10(n=10)个元素
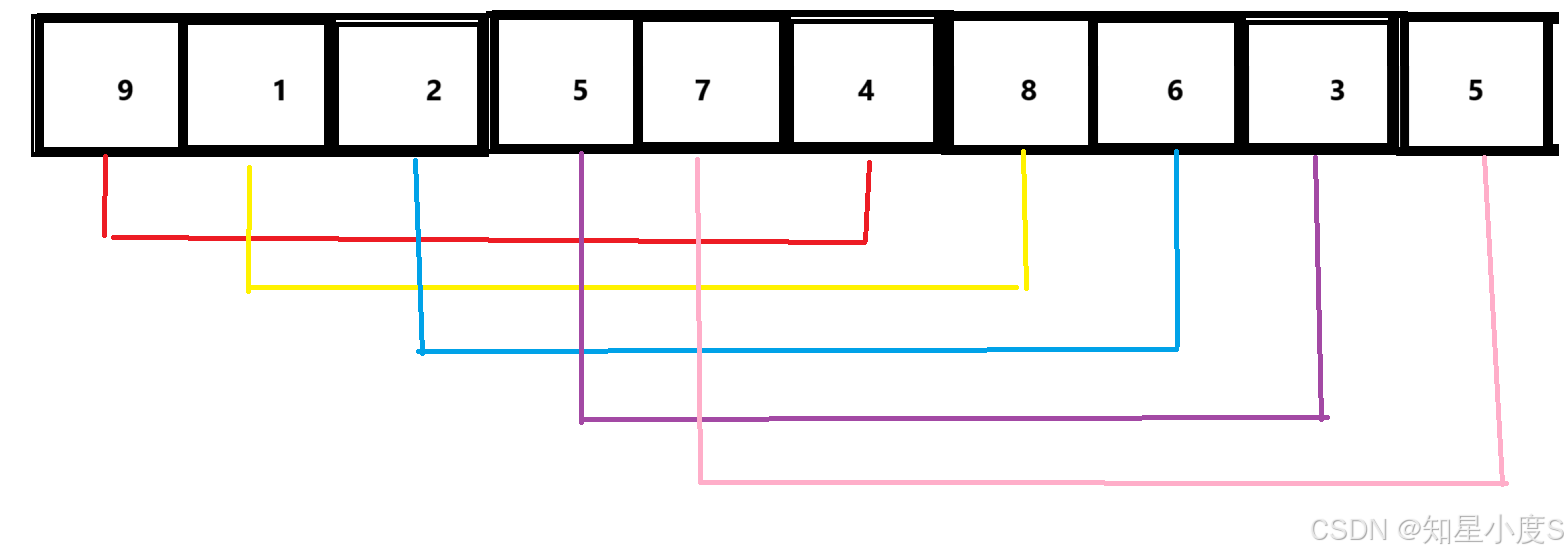
这里为了方便画图,首先我们取gap = 5,将需要排序的数组分为5组(这里的分组依据是距离相等的记录分在同⼀组内)
那么,我们这里就进行了【9,4】,【1,8】,【2,6】,【5,3】,【7,5】这样的分组,分组完成之后我们就排序每一组内部的数据~排升序就变成【4,9】,【1,8】,【2,6】,【3,5】,【5,7】,那么我们得到新的数组就是【4,1,2,3,5,9,8,6,5,7】,我们会发现经过第一轮排序我们把小的数据放在了前面,大的数据放在了后面~
继续让gap = gap/3+1=2,将数据分为两组,每一组有5个数据
一组数据是【4,2,5,8,5】,一组数据是【1,3,9,6,7】,再对每一组数据进行排序,第一组就是【2,4,5,5,8】,第二组就是【1,3,6,7,9】,恢复到原来的数据就变成了【2,1,4,3,5,6,5,7,8,9】,接下来数据已经更加有序了,那么接下来我们就可以继续取gap=gap/3+1,这个时候gap已经等于1了,就相当于将数据分为一组,那么这个时候就相当于我们的直接插入排序进行排序了~
这里简单走一下过程~也更好地理解一下直接插入排序~
1.tmp = 1
| 1 | 2 | 4 | 3 | 5 | 6 | 5 | 7 | 8 | 9 |
2.tmp = 4
| 1 | 2 | 4 | 3 | 5 | 6 | 5 | 7 | 8 | 9 |
3.tmp = 3
| 1 | 2 | 3 | 4 | 5 | 6 | 5 | 7 | 8 | 9 |
4.tmp = 5
| 1 | 2 | 3 | 4 | 5 | 6 | 5 | 7 | 8 | 9 |
5.tmp = 6
| 1 | 2 | 3 | 4 | 5 | 6 | 5 | 7 | 8 | 9 |
6.tmp = 5
| 1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 |
…………
最终得到升序数组
| 1 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 |
代码
希尔排序思想理解了,那么怎么写代码呢?公主王子~请看下面的代码~
//希尔排序
void ShellSort(int* arr, int sz)
{
//给一个变量gap
int gap = sz;
while (gap > 1)
{
gap = gap / 3 + 1;//通常情况下,我们这样确定gap的值
//数据分为gap组,排序每一组
//这里的gap也代表着每一组数据相差的下标
for (int i = 0; i < sz - gap; i++)
{
//每一组进行组内排序
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
//跳出循环两种情况
//1.end越界(end = -1)说明tmp是当前组最小的
//2.arr[end] < tmp
arr[end + gap] = tmp;
}
}
}排序成功~
常见问题:
1,为什么外层循环条件不是gap>=1?
注意,以上面的例子为例,最开始我们让gap=n=10,第一次进入循环gap=gap/3+1=4>1,第二次进入循环gap=gap/3+1=2>1,第三次进入循环gap=gap/3+1= 1,这里已经gap=1了,就不需要再进入一次循环~
2.为什么i < sz-gap ?
这里我们需要确保数组下标有效,后面的end+gap=i+gap<sz,所以i < sz-gap 。
时间复杂度
有人一看这希尔排序三层循环,肯定时间复杂度大于直接插入排序,事实上并不是这样。
1. 希尔排序是对直接插入排序的优化。2. 当 gap > 1 时都是预排序,目的是让数组更接近于有序。当 gap == 1 时,数组已经接近有序, 这样就会很快。整体来看,可以达到优化的效果。
希尔排序的时间复杂度估算:外层循环:外层循环的时间复杂度(取决于gap怎么样取值): O (log 2 n ) 或者 O (log 3 n ) ,即 O (log n )内层循环:希尔排序在最初和最后的排序的次数都为n,即前⼀阶段排序次数是逐渐上升的状态,当到达某⼀顶点时,排序次数逐渐下降到n~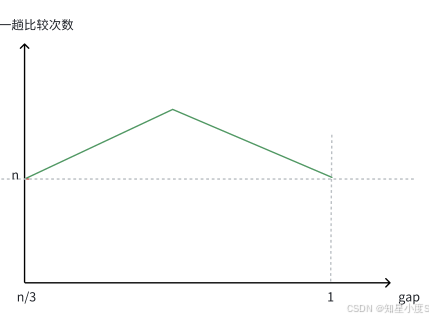 所以希尔排序时间复杂度是很难计算的~根据一些资料,我们一般认为 希尔排序时间复杂度为O(N^1.3),这明显小于直接插入排序的O(N^2)
所以希尔排序时间复杂度是很难计算的~根据一些资料,我们一般认为 希尔排序时间复杂度为O(N^1.3),这明显小于直接插入排序的O(N^2)
比较时间
有的可能还是不相信希尔排序效率高于直接插入排序,我们来进行简单的验证~
这里首先来了解几个函数~
rand:
功能:产生随机值,从srand (seed)中指定的seed开始,返回一个[seed, RAND_MAX(0x7fff))间的随机整数。
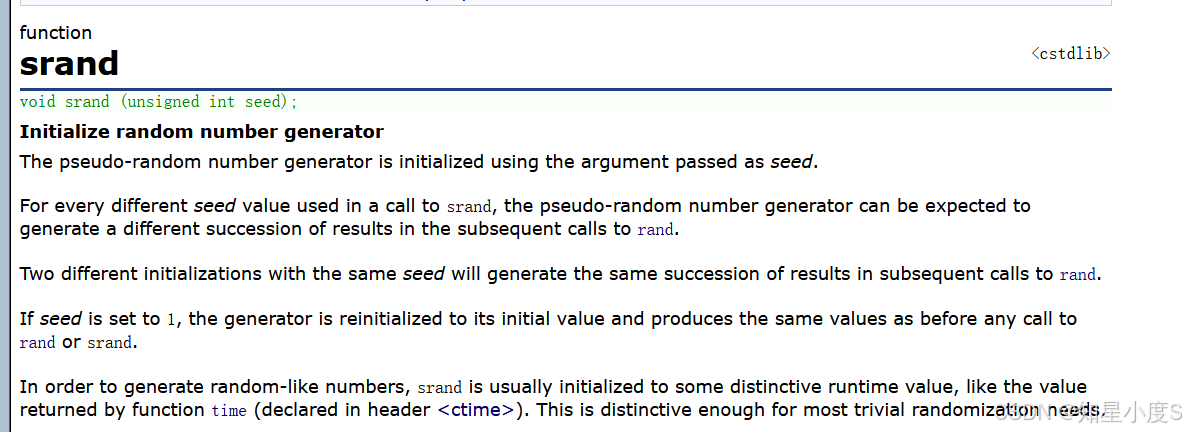
srand:
参数seed是rand()的种子,用来初始化rand()的起始值。
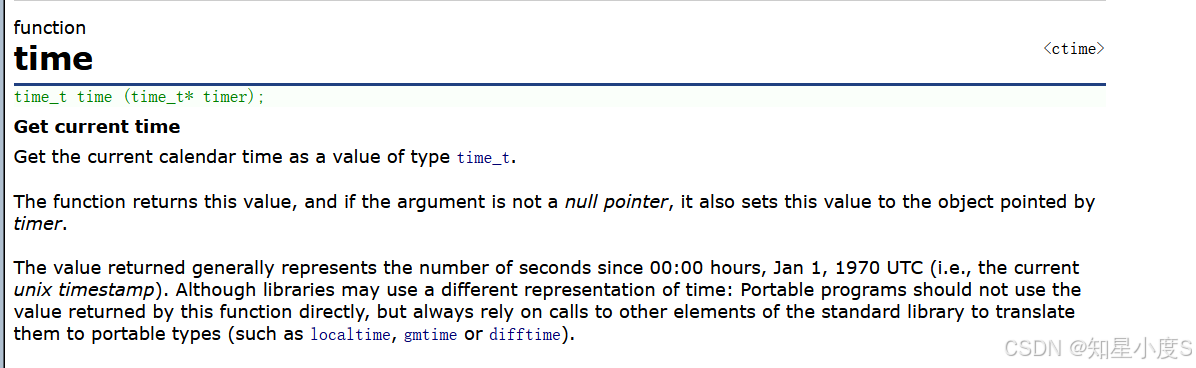
time:
如果希望rand()在每次程序运行时产生的值都不一样,必须给srand(seed)中的seed一个变值,这个变值必须在每次程序运行时都不一样(比如到目前为止流逝的时间),我们知道时间是无时无刻都在变化的~我们就可以使用srand(time(0))
clock:
C语言中的
clock()函数是一个标准库函数,它用于测量程序自某个特定时间点(通常默认为程序启动时)以来所消耗的CPU时钟周期数(可以简单理解为运行到当前代码的时间)。这个函数返回的是CLOCKS_PER_SEC常量表示的秒级时间戳,通常在大多数系统上,CLOCKS_PER_SEC等于CLOCKS_PER_SEC大约等于1000(毫秒)或者1000000(纳秒),VS编译器是ms(毫秒)。
接下来就可以写出测试代码:
//测试排序效率
void testOP()
{
srand(time(0));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
for (int i = 0; i < N; i++)
{
a1[i] = rand();//生成随机数放入数组中
a2[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
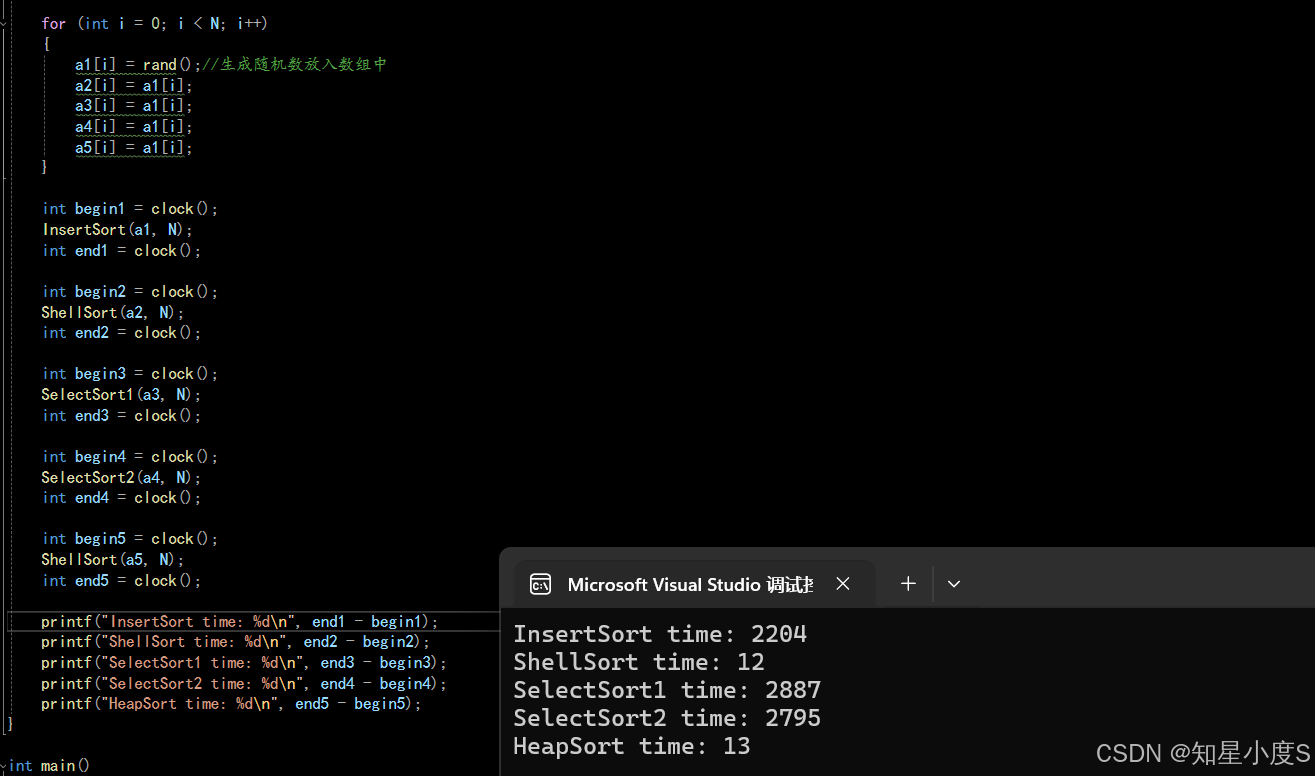
printf("InsertSort time: %d\n", end1 - begin1);
printf("ShellSort time: %d\n", end2 - begin2);
}
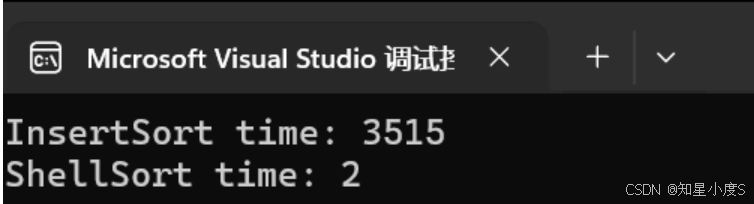
直接插入排序时间3515ms,希尔排序2ms,显然希尔排序是优于直接插入排序的~
选择排序
直接选择排序
在前面的博客中,我们提到过这种排序方法,我们也把它叫做选择法排序~
基本思想
1. 在 元素集合 array[i]--array[n-1] 中选择关键码最⼤(⼩)的数据元素2. 若 它不是这组元素中的最后⼀个(第⼀个)元素,则将它与这组元素中的最后⼀个(第一个)元素交换3. 在剩余的 array[i]--array[n-2] ( array[i+1]--array[n-1] ) 集合中,重复上述步骤,直到集合剩余 1 个元素
以排序【9,1,2,5,7,4,8,6,3,5】这个数组为例,我们首先想把最小的数据放在第一个位置,记录下当前位置(i=0)的下标,往后面走找到最小的数据的下标(i=1),然后进行交换,依此类推,直到数据只剩下一个元素就停止~
代码
for循环版本:
//交换数据
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//直接选择排序
void SelectSort(int* arr, int sz)
{
for (int j = 0; j < sz - 1; j++)
{
int mini = j;//记录最小元素下标
for (int i = j + 1; i < sz; i++)
{
//往后面遍历找当前最小元素
if (arr[i] < arr[mini])
{
mini = i; //记录记录最小元素下标
}
}
//如果mini!=j,就进行交换
if (mini != j)
{
Swap(&arr[mini], &arr[j]);
}
}
}排序成功~
这里我们也可以给他优化一下,同时遍历找当前最大和最小的元素~
//交换数据
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//直接选择排序
void SelectSort(int* arr, int sz)
{
for (int j = 0; j < sz / 2; j++)
{
int mini = j;//记录最小元素下标
int maxi = sz - 1 - j;//记录最大元素下标
//因为同时找最大和最小元素,所以查找范围是j~(sz-1-j)
for (int i = j; i < sz - 1 - j; i++)
{
//往后面遍历找当前最小元素
if (arr[i] < arr[mini])
{
mini = i; //记录当前最小元素下标
}
//往后面遍历找当前最大元素
if (arr[i] > arr[maxi])
{
maxi = i; //记录当前最大元素下标
}
}
//如果mini!=j,就进行交换
if (mini != j)
{
Swap(&arr[mini], &arr[j]);
}
//如果maxi!=(sz-1-j),就进行交换
if (maxi != (sz - 1 - j))
{
Swap(&arr[maxi], &arr[sz - 1 - j]);
}
}
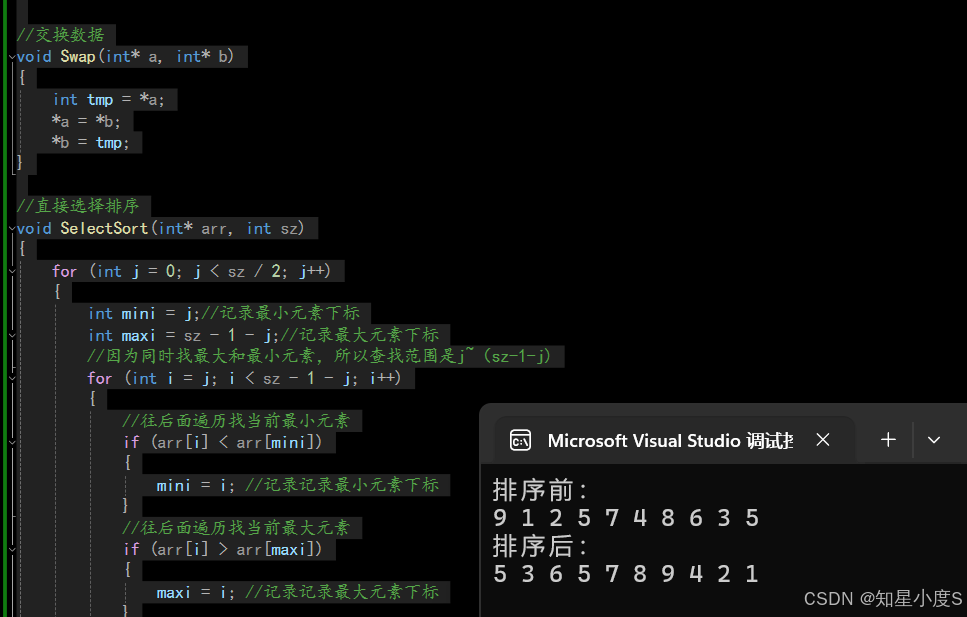
}自信满满的写好代码,但是排序结果却是错误的~别急我们分析看看~
第一次进入循环:
初始:mini = 0,maxi=9,第二层循环结束后mini=1,maxi=0
交换arr[mini]和arr[j]——>arr[0]=1,arr[1]=9
再一次交换arr[maxi]和arr[sz-1-j]——>arr[0]=5,arr[9]=1
问题是不是就出现了,当我们的最大元素下标就是开始的位置时就出现了问题,因为我们前面已经交换了元素位置,所以这里就需要进行特殊处理一下~如果maxi=j,就让maxi提前走到mini的位置
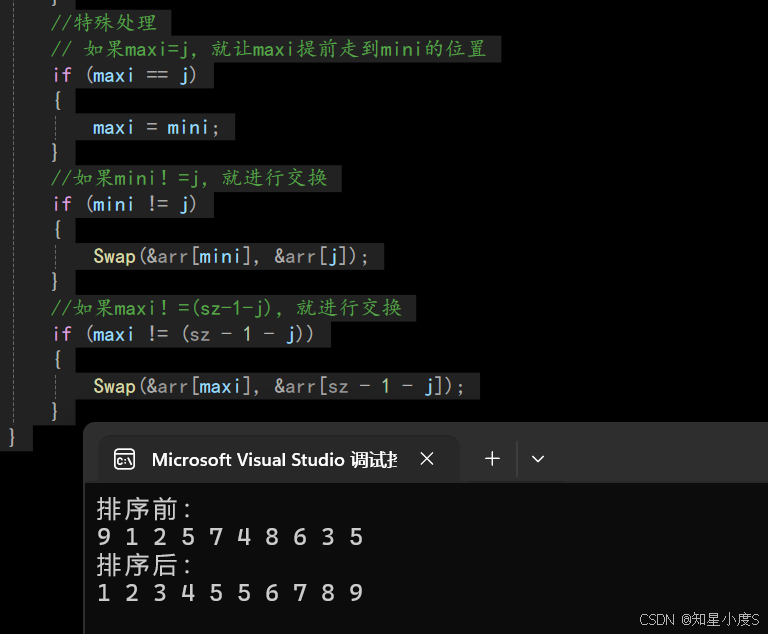
正确代码:
//交换数据
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//直接选择排序
void SelectSort(int* arr, int sz)
{
for (int j = 0; j < sz / 2; j++)
{
int mini = j;//记录最小元素下标
int maxi = sz - 1 - j;//记录最大元素下标
//因为同时找最大和最小元素,所以查找范围是j~(sz-1-j)
for (int i = j; i < sz - 1 - j; i++)
{
//往后面遍历找当前最小元素
if (arr[i] < arr[mini])
{
mini = i; //记录当前最小元素下标
}
//往后面遍历找当前最大元素
if (arr[i] > arr[maxi])
{
maxi = i; //记录当前最大元素下标
}
}
//特殊处理
// 如果maxi=j,就让maxi提前走到mini的位置
if (maxi == j)
{
maxi = mini;
}
//如果mini!=j,就进行交换
if (mini != j)
{
Swap(&arr[mini], &arr[j]);
}
//如果maxi!=(sz-1-j),就进行交换
if (maxi != (sz - 1 - j))
{
Swap(&arr[maxi], &arr[sz - 1 - j]);
}
}
}这一次才真正的排序成功~
前面是两层for循环版本,接下来还有一个版本是外层while循环,内层for循环版本~
代码:
//直接选择排序
void SelectSort2(int* arr, int sz)
{
int begin = 0;
int end = sz - 1;
//begin、end分别表示开头位置和结尾位置
while(begin < end)
{
int mini = begin;//记录最小元素下标
int maxi = end;//记录最大元素下标
//因为同时找最大和最小元素,所以查找范围是begin~end
for (int i = begin; i <= end; i++)
{
//往后面遍历找当前最小元素
if (arr[i] < arr[mini])
{
mini = i; //记录当前最小元素下标
}
//往后面遍历找当前最大元素
if (arr[i] > arr[maxi])
{
maxi = i; //记录当前最大元素下标
}
}
//特殊处理
// 如果maxi==begin,就让maxi提前走到mini的位置
if (maxi == begin)
{
maxi = mini;
}
//1.
if (mini != begin)
{
Swap(&arr[mini], &arr[begin]);
}
if (maxi != end)
{
Swap(&arr[maxi], &arr[end]);
}
//2.也可以不判断直接交换,就是自己和自己交换
/*Swap(&arr[mini], &arr[begin]);
Swap(&arr[maxi], &arr[end]);*/
begin++;
end--;
}
}排序成功~
时间复杂度
显然
1. 直接选择排序思考非常好理解,但是效率不是很好,实际中很少使用2. 时间复杂度: O ( N ^2 )3. 空间复杂度: O (1)

堆排序
思路及代码
另外一种选择排序就是堆排序了~堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的⼀种排序算法,排升序要建大堆,排降序建小堆~这里我们给出代码~有疑问的可以再看看这一篇博客~数据结构——二叉树
//向下调整数据
AdjustDown(HPDataType* arr, int parent, int size)
{
assert(arr);
//当前父结点的左孩子结点
int child = 2 * parent + 1;
while (child < size)
//左孩子结点编号必须小于结点个数
{
//如果右孩子结点存在!!!
// 并且右孩子结点>左孩子结点,那么child就是右孩子结点编号
if (child + 1 < size && (arr[child + 1] > arr[child]))
{
child++;
}
//如果父结点小于孩子结点就进行交换
if (arr[parent] < arr[child])
{
Swap(&arr[parent], &arr[child]);
//继续往下面调整
parent = child;
child = 2 * parent + 1;
}
//如果父结点大于孩子结点就提前结束循环
else
{
break;
}
}
}
void HeapSort(int* arr, int sz)
{
//根据给定的arr建堆
//调整数组arr的数据
//1.向下的算法建堆
//child = sz - 1(最大的孩子结点下标)
//parent = ( sz - 1 - 1)/2 (最大的父结点下标)
int i = 0;
for (i = (sz - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(arr, i, sz);
//AdjustDown参数//AdjustDown(HPDataType* arr, int parent, int size)
}
//2.向上的算法建堆
//for(i = 0;i < sz; i++)
//{
// AdjustUP(arr, i);
// //AdjustUP参数//AdjustUP(HPDataType* arr, int child)
//}
//进行堆排序
//升序——大堆
// 堆顶元素就是当前最大的,交换之后最后面的元素最大
//降序——小堆
//堆顶元素就是当前最小的,交换之后最后面的元素最小
int end = sz - 1;
while (end > 0)
{
//一个个调整
Swap(&arr[0], &arr[end]);
//堆顶元素就是当前最大的,交换之后最后面的元素最大
AdjustDown(arr, 0, end);
//这里end就代表调整个数
// 数组下标为end的元素已经是最大的不需要调整
//最后面元素变化
end--;
}
}
时间复杂度
通过前面的博客,我们知道堆排序时间复杂度为O(N*lgN),这里我们来测试一下它排序十万个数据要花的时间~
这一篇博客有关于排序的内容就结束啦~想了解更多的排序内容~请看下集~
♥♥♥本篇博客内容结束,期待与各位优秀程序员交流,有什么问题请私信♥♥♥
♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥
✨✨✨✨✨✨个人主页✨✨✨✨✨✨