一、向量叉乘的知识点
-
定义与公式:
- 向量叉乘的定义为:对于两个三维向量a和b,它们的叉乘结果是一个向量c,记为c=a×b。
- 叉乘的计算公式为:c=(y1z2-y2z1)i+(x2z1-x1z2)j+(x1y2-x2y1)k,其中a=(x1, y1, z1),b=(x2, y2, z2),i、j、k分别为x、y、z轴的单位向量。
-
几何意义:
- 叉乘得到的向量c与向量a和b都垂直,即c⊥a且c⊥b。
- 叉乘结果向量c的方向遵循右手定则(在Unity中为左手定则):将右手四指从向量a转向向量b,拇指的指向即为向量c的方向。
- 叉乘结果向量c的模长等于向量a和b的模长与它们之间夹角的正弦值的乘积,即|c|=|a|×|b|×sinθ。
-
性质:
- 叉乘不满足交换律,即a×b≠b×a,而是a×b=-(b×a)。
- 叉乘满足加法的分配律,即a×(b+c)=a×b+a×c。
- 叉乘结果是一个向量,而不是标量。
点乘(Dot Product):
点乘的顺序是可以互换的。即,对于任意两个向量A和B,有A · B = B · A。点乘的结果是一个标量(scalar),表示两个向量之间的夹角余弦值乘以它们的模的乘积。由于余弦函数是对称的,所以点乘也是对称的。
叉乘(Cross Product):
叉乘的顺序则不能互换。对于向量A和B,A × B和B × A的结果是不同的。实际上,A × B和B × A是互为相反向量,即A × B = -(B × A)。叉乘的结果是一个向量(vector),这个向量垂直于原两个向量所构成的平面,并且其方向由右手定则决定。
因此,在使用叉乘时,必须注意向量的顺序,因为顺序的不同会导致结果向量的方向相反。而在使用点乘时,则不需要担心向量的顺序问题。
一、相关API
在Unity3D中,叉乘运算可以通过Vector3.Cross方法来实现。该方法的签名如下:
public static Vector3 Cross(Vector3 lhs, Vector3 rhs); |
其中,lhs和rhs是需要进行叉乘的两个向量,返回结果是它们的叉乘向量。
三、使用场景
- 计算法向量:在3D图形学中,叉乘常用于计算表面的法向量。例如,给定两个不共线的表面向量,可以通过叉乘得到它们的法向量,这在光照计算中非常重要。
- 确定旋转轴:在旋转操作中,叉乘可以用于确定旋转轴。例如,计算物体从当前方向向量旋转到目标方向向量所需的旋转轴。
- 碰撞检测:在碰撞检测中,叉乘可以用于计算碰撞法线和碰撞响应的方向。
- 判断左右方位:通过叉乘的结果,可以判断一个物体相对于另一个物体的左右方位。例如,在游戏中判断敌人位于玩家的左侧还是右侧。
四、注意事项
- 向量顺序:叉乘的结果依赖于向量的顺序。即
A × B和B × A的结果方向相反。因此,在使用叉乘时,必须注意向量的顺序。 - 零向量:任何向量与零向量进行叉乘的结果都是零向量。因此,在进行叉乘运算前,应确保参与运算的向量不是零向量。
- 共线向量:如果两个向量共线(即它们平行或反向平行),则它们的叉乘结果为零向量。这是因为共线向量无法构成一个具有面积的平行四边形。
- 左手坐标系:Unity3D使用的是左手坐标系,这与数学上常用的右手坐标系有所不同。因此,在使用叉乘确定方向时,需要注意坐标系的差异。在Unity中,应使用左手法则来判断叉乘结果的方向。
综上所述,叉乘在Unity3D中有着广泛的应用和独特的几何意义。通过合理利用叉乘运算和相关API,可以实现许多复杂的3D图形和物理效果。同时,在使用叉乘时也需要注意向量顺序、零向量、共线向量以及坐标系差异等问题。
五、代码示例
public class chacheng : MonoBehaviour
{
public Transform A;
public Transform B;
void Start()
{
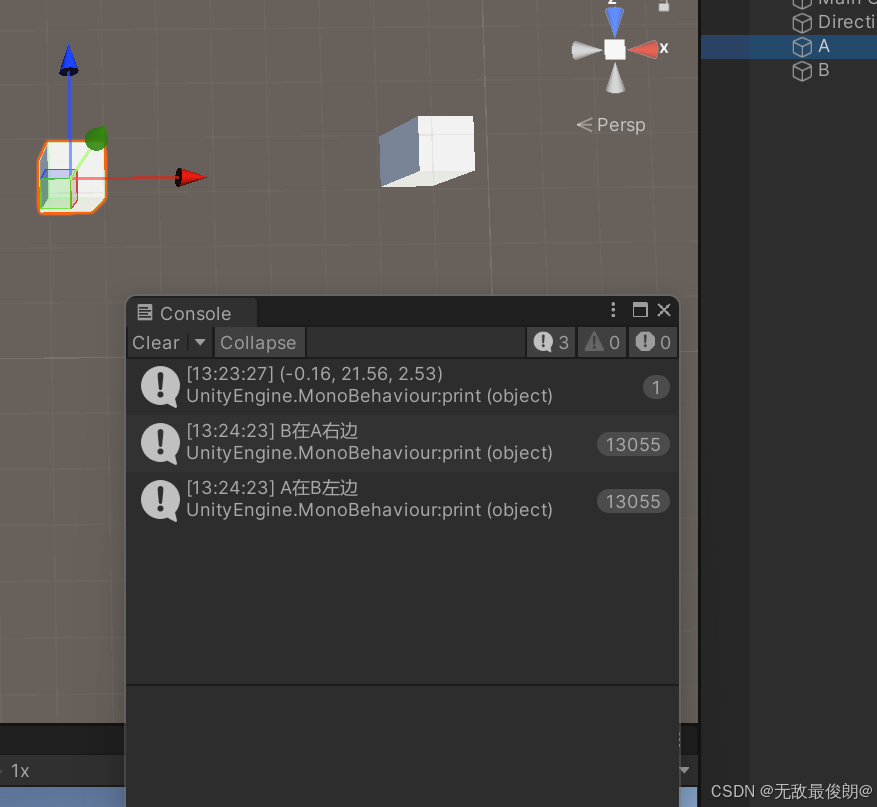
print(Vector3.Cross(A.position, B.position));
}
void Update()
{
//假设向量 A和B 都在 XZ平面上
//向量A 叉乘 向量 B
//y大于0 证明 B在A右侧
//y小于0 证明 B在A左侧
Vector3 rev = Vector3.Cross(A.position, B.position);
if(rev.y > 0)
{
print("B在A右边");
}
else
{
print("B在A左边");
}
Vector3 rev1 = Vector3.Cross(B.position, A.position);
if (rev1.y > 0)
{
print("A在B右边");
}
else
{
print("A在B左边");
}
}
}结果: