目录
1、最长递增子序列
1.1 算法原理
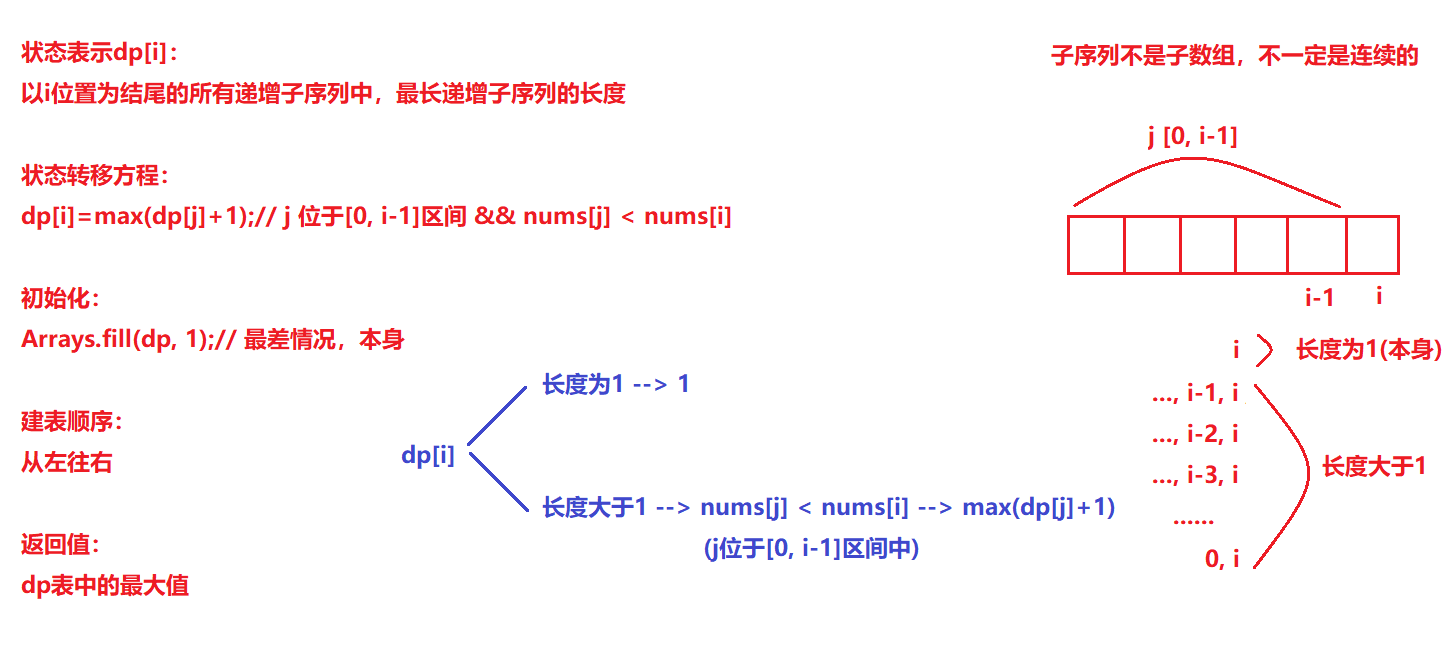
- 状态表示dp[i]:
以i位置为结尾的所有递增子序列中,最长递增子序列的长度
- 状态转移方程:
dp[i]=max(dp[j]+1);// j 位于[0, i-1]区间 && nums[j] < nums[i]
- 初始化:
Arrays.fill(dp, 1);// 最差情况,本身
- 建表顺序:
从左往右
- 返回值:
dp表中的最大值
1.2 算法代码
class Solution {
public int lengthOfLIS(int[] nums) {
int n = nums.length;
int[] dp = new int[n];
// 初始化(最差情况: 本身)
Arrays.fill(dp, 1);
int ret = 1;
// 建表
for(int i = 1; i < n; i++) {
// j -> [0, i-1]
for(int j = i - 1; j >= 0; j--) {
if(nums[j] < nums[i]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
ret = Math.max(ret, dp[i]);
}
return ret;
}
}2、摆动序列
2.1 算法原理
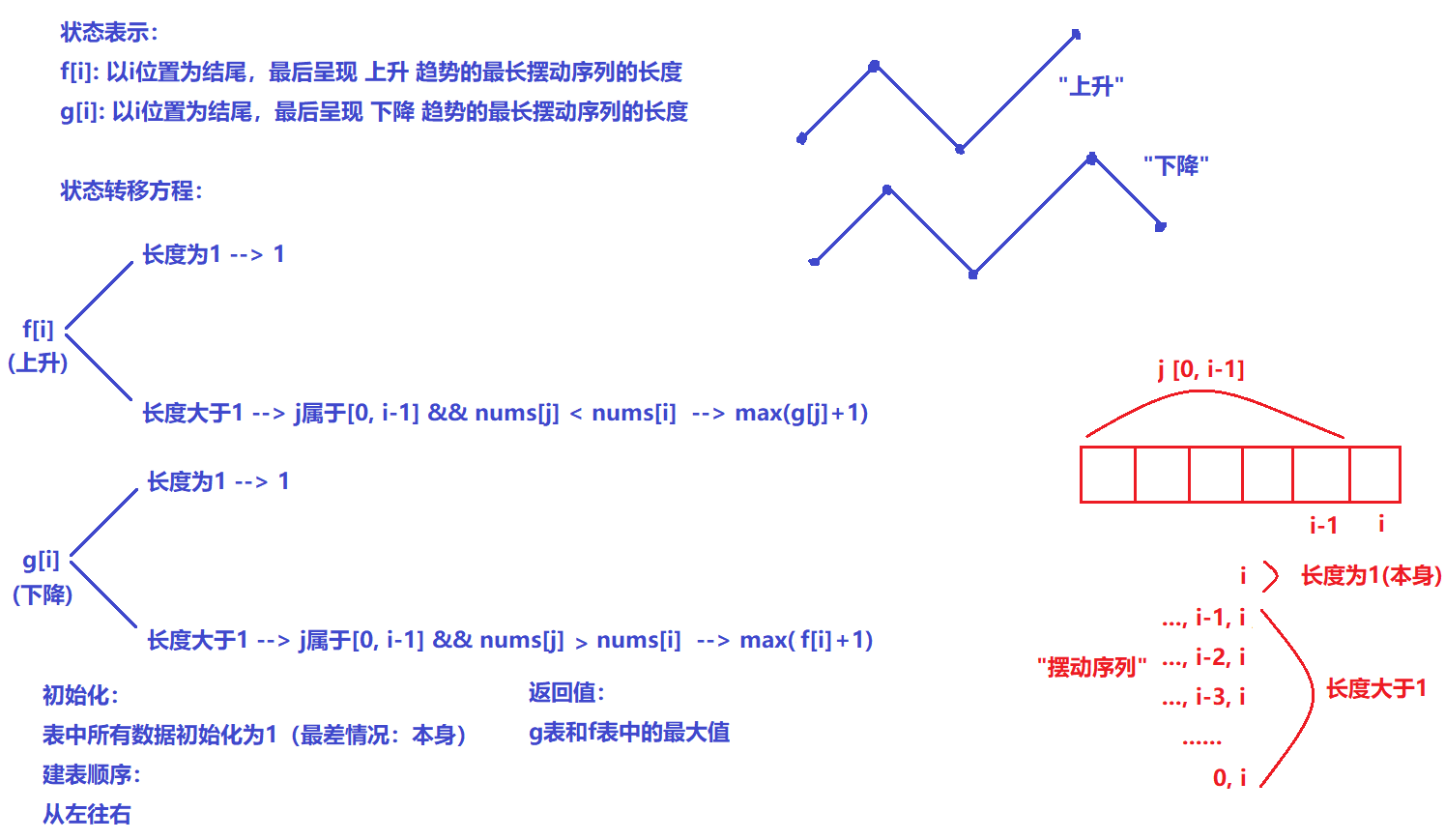
- 状态表示:
f[i]: 以i位置为结尾,最后呈现 上升 趋势的最长摆动序列的长度
g[i]: 以i位置为结尾,最后呈现 下降 趋势的最长摆动序列的长度
- 状态转移方程:
f[i] = max(g[j] + 1);
g[i] = max(f[j] + 1);
- 初始化:
f表、g表中所有元素初始化为1
- 建表顺序:
从左往右
- 返回值:
g表和f表中的最大值
2.2 算法代码
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
// f[i]: 以i位置为结尾,最后呈现 上升 趋势的最长摆动序列的长度
// g[i]: 以i位置为结尾,最后呈现 下降 趋势的最长摆动序列的长度
int[] f = new int[n];
int[] g = new int[n];
// 初始化
Arrays.fill(f, 1);
Arrays.fill(g, 1);
int ret = 1;
// 填表
for (int i = 1; i < n; i++) {
// j -> [0, i-1]
for(int j = i - 1; j >= 0; j--) {
if(nums[j] > nums[i]) {
g[i] = Math.max(f[j] + 1, g[i]);
}
if(nums[j] < nums[i]) {
f[i] = Math.max(g[j] + 1, f[i]);
}
}
ret = Math.max(ret, Math.max(g[i], f[i]));
}
return ret;
}
}3、最长递增子序列的个数
3.1 算法原理
- 状态表示:
count[i]:以i位置为结尾的所有子序列中,最长的递增子序列的 "个数"
len[i]:以i位置为结尾的所有子序列中,最长的递增子序列的 "长度"
- 状态转移方程:
len[j]+1==len[i] --> count[i] += count[j]
len[j]+1 < len[i] --> 无视
len[j]+1 > len[i] --> count[i]=count[j] && len[i]=len[j]+1
- 初始化:
两个表中的所有元素初始化为1(最差情况下)
- 建表顺序:
从左往右
- 返回值:
返回最长长度的递增子序列的"总个数"(求和)
3.2 算法代码
class Solution {
public int findNumberOfLIS(int[] nums) {
int n = nums.length;
int[] len = new int[n];// 最长递增子序列的长度
int[] count = new int[n];// 最长递增子序列的个数
// 初始化
Arrays.fill(len, 1);
Arrays.fill(count, 1);
// 最长长度 / 最大个数
int retLen = 1, retCount = 1;
// 填表
for(int i = 1; i < n; i++) {
for(int j = i - 1; j >= 0; j--) {
// 同时处理两个表
if(nums[j] < nums[i]) {
if(len[j] + 1 == len[i]) count[i] += count[j];
else if(len[j] + 1 > len[i]) {
len[i] = len[j] + 1;
count[i] = count[j];
}
}
}
// 同时处理返回值
if(retLen == len[i]) retCount += count[i];
else if(retLen < len[i]) {
retLen = len[i];
retCount = count[i];
}
}
return retCount;
}
}4、最长数对链
4.1 算法原理
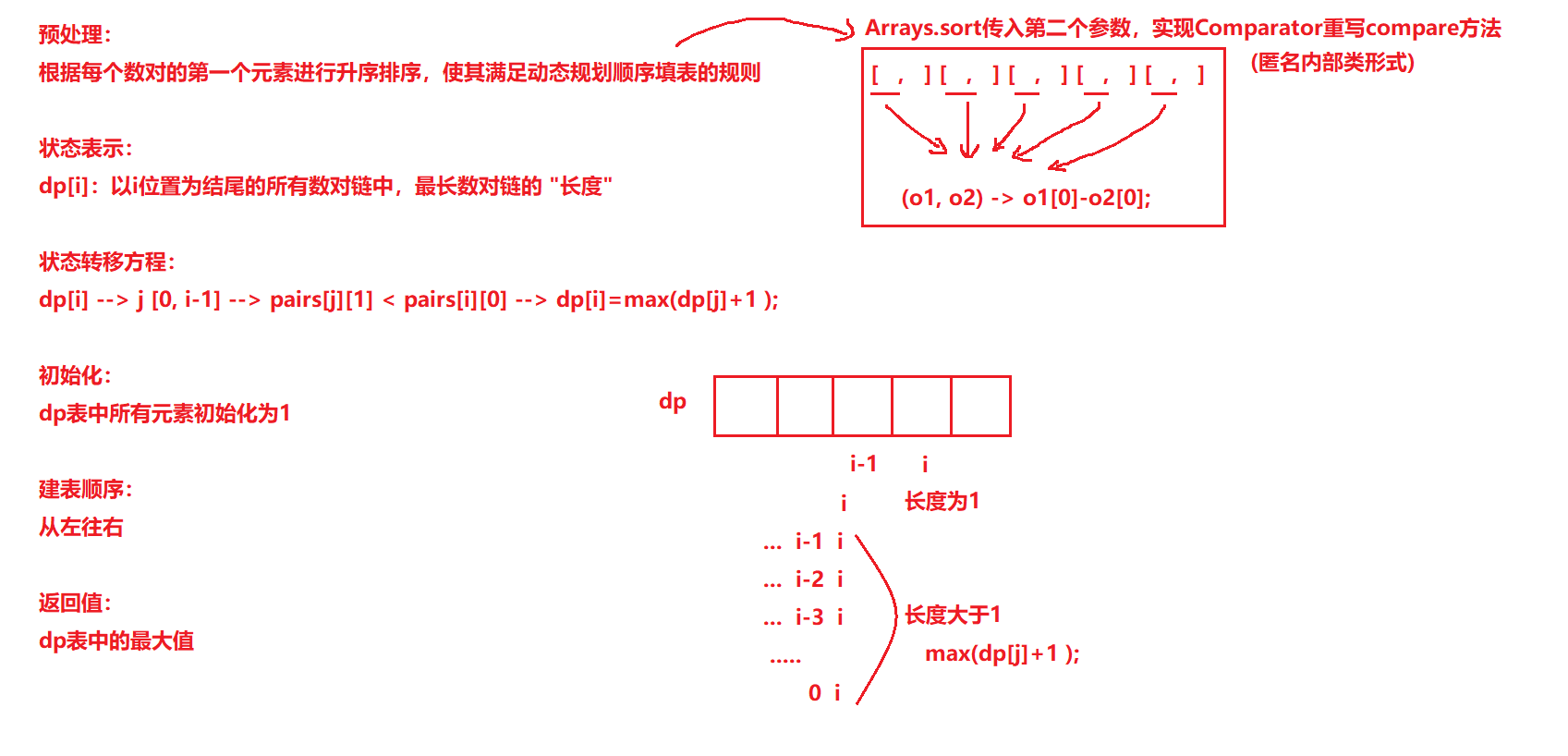
预处理:根据每个数对的第一个元素进行升序排序,使其满足动态规划顺序填表的规则
- 状态表示:
dp[i]:以i位置为结尾的所有数对链中,最长数对链的 "长度"
- 状态转移方程:
dp[i] --> j [0, i-1] --> pairs[j][1] < pairs[i][0] --> dp[i]=max(dp[j]+1 );
- 初始化:
dp表中所有元素初始化为1
- 建表顺序:
从左往右
- 返回值:
dp表中的最大值
4.2 算法代码
class Solution {
public int findLongestChain(int[][] pairs) {
// 预处理: 根据数对链的第一个元素进行升序排序 --> 满足动态规划顺序填表的要求
Arrays.sort(pairs, (o1, o2) -> o1[0] - o2[0]);
int n = pairs.length;
int[] dp = new int[n];
// 初始化
Arrays.fill(dp, 1);
int ret = 1;
// 填表
for(int i = 1; i < n; i++) {
for(int j = i - 1; j >= 0; j--) {
if(pairs[i][0] > pairs[j][1]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
ret = Math.max(ret, dp[i]);
}
return ret;
}
}5、最长定差子序列
5.1 算法原理
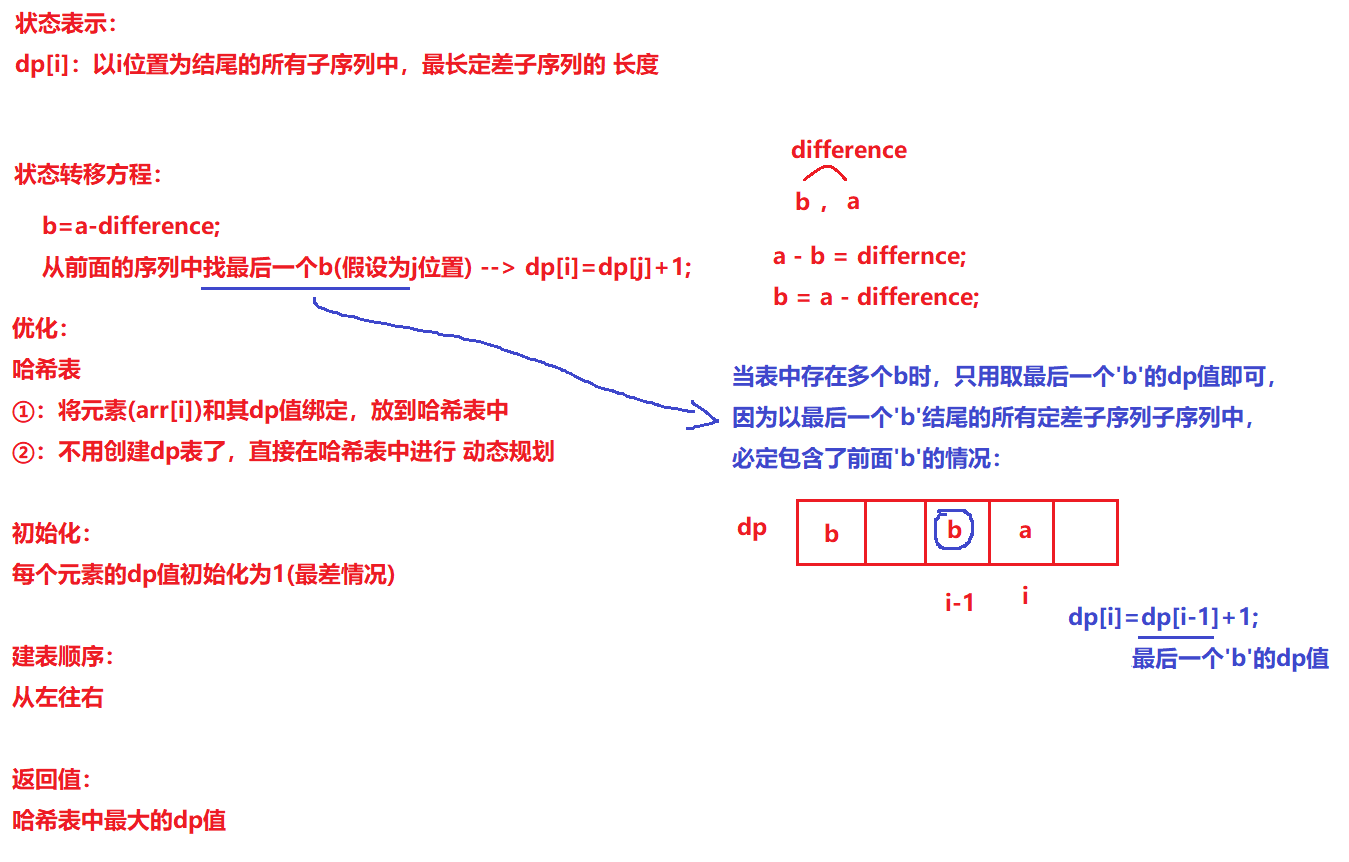
- 状态表示:
dp[i]:以i位置为结尾的所有子序列中,最长定差子序列的 长度
- 状态转移方程:
b=a-difference;
从前面的序列中找最后一个b(假设为j位置) --> dp[i]=dp[j]+1;
优化:哈希表
①:将元素(arr[i])和其dp值绑定,放到哈希表中
②:不用创建dp表了,直接在哈希表中进行 动态规划③:Map天然的去重特性
- 初始化:
每个元素的dp值初始化为1(最差情况)
- 建表顺序:
从左往右
- 返回值:
哈希表中最大的dp值
5.2 算法代码
class Solution {
public int longestSubsequence(int[] arr, int difference) {
int n = arr.length;
// <元素, 最长长度>
Map<Integer, Integer> hash = new HashMap<>();
int ret = 1;
for(int i = 0; i < n; i++) {
// 找上一个等差值
int b = arr[i] - difference;
int len = hash.getOrDefault(b, 0) + 1;
hash.put(arr[i], len);
ret = Math.max(ret, len);
}
return ret;
}
}6、最长的斐波那契子序列的长度
6.1 算法原理
- 状态表示:
dp[i][j]:以i位置(前)以及j位置(后)元素结尾的所有子序列中,最长的斐波那契子序列的长度
- 状态转移方程:
j位置元素为c,i位置元素为b,k位置元素为a,则a=c-b
1. a不存在 --> 2
2. a存在,但 i<k<j --> 2
3. a存在,且合法(k<i<j) --> dp[k][i]+1;
- 建表顺序
从上往下
- 返回值:
dp表中的最大值
处理特殊情况:return ret == 2 ? 0 : ret ;
6.2 算法代码
class Solution5 {
public int lenLongestFibSubseq(int[] arr) {
int n = arr.length;
// <元素值, 下标>
Map<Integer, Integer> hash = new HashMap<>();
for(int i = 0; i < n; i++) hash.put(arr[i], i);
int[][] dp = new int[n][n];
// 初始化
for(int i = 0; i < n; i++) Arrays.fill(dp[i], 2);
int ret = 0;
// 从上往下填表
for(int j = 2; j < n; j++) {
for(int i = 1; i < j; i++) {
int x = arr[j] - arr[i];
int index = hash.getOrDefault(x, -1);
if(index != -1 && index < i) {
dp[i][j] = dp[index][i] + 1;
ret = Math.max(ret, dp[i][j]);
}
}
}
return ret;
}
}7、最长等差数列
7.1 算法原理
- 状态表示:
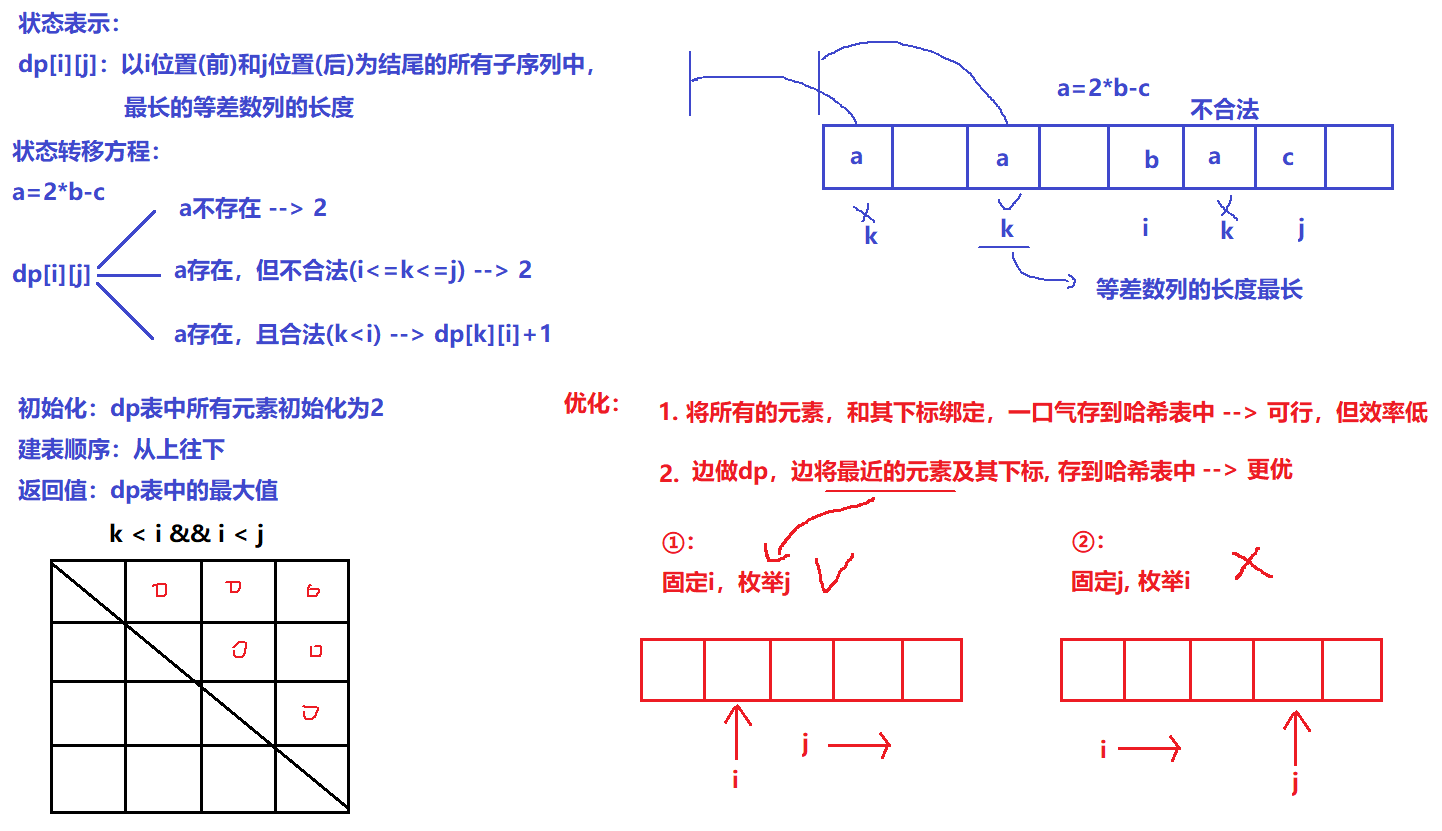
dp[i][j]:以i位置(前)和j位置(后)为结尾的所有子序列中,最长的等差数列的长度
- 状态转移方程:
dp[i][j] = dp[k][j] + 1;(k存在且合法)
- 初始化:
dp表中所有元素初始化为2
- 建表顺序:
从上往下
- 返回值:
dp表中的最大值
优化:
边做dp,边将最近的元素及其下标, 存到哈希表中:固定i,枚举j
7.2 算法代码
class Solution {
public int longestArithSeqLength(int[] nums) {
int n = nums.length;
// dp[i][j]: 以(i, j)位置为结尾的所有子序列中,最长等差数列的长度
int[][] dp = new int[n][n];
// 优化 -> 将最近的元素放进哈希表中
// <元素, 元素下标>
Map<Integer, Integer> hash = new HashMap<>();
hash.put(nums[0], 0);
// 初始化
for (int i = 0; i < n; i++) Arrays.fill(dp[i], 2);
int ret = 2;
// 建表(固定倒数第二个数, 枚举倒数第一个数)
for (int i = 1; i < n; i++) {
for(int j = i + 1; j < n; j++) {
int val = nums[i] * 2 - nums[j];
int index = hash.getOrDefault(val, -1);
if(index != -1) {
dp[i][j] = dp[index][i] + 1;
ret = Math.max(ret, dp[i][j]);
}
}
hash.put(nums[i], i);
}
return ret;
}
}8、等差数列划分 II - 子序列(hard)
8.1 算法原理
- 状态表示:
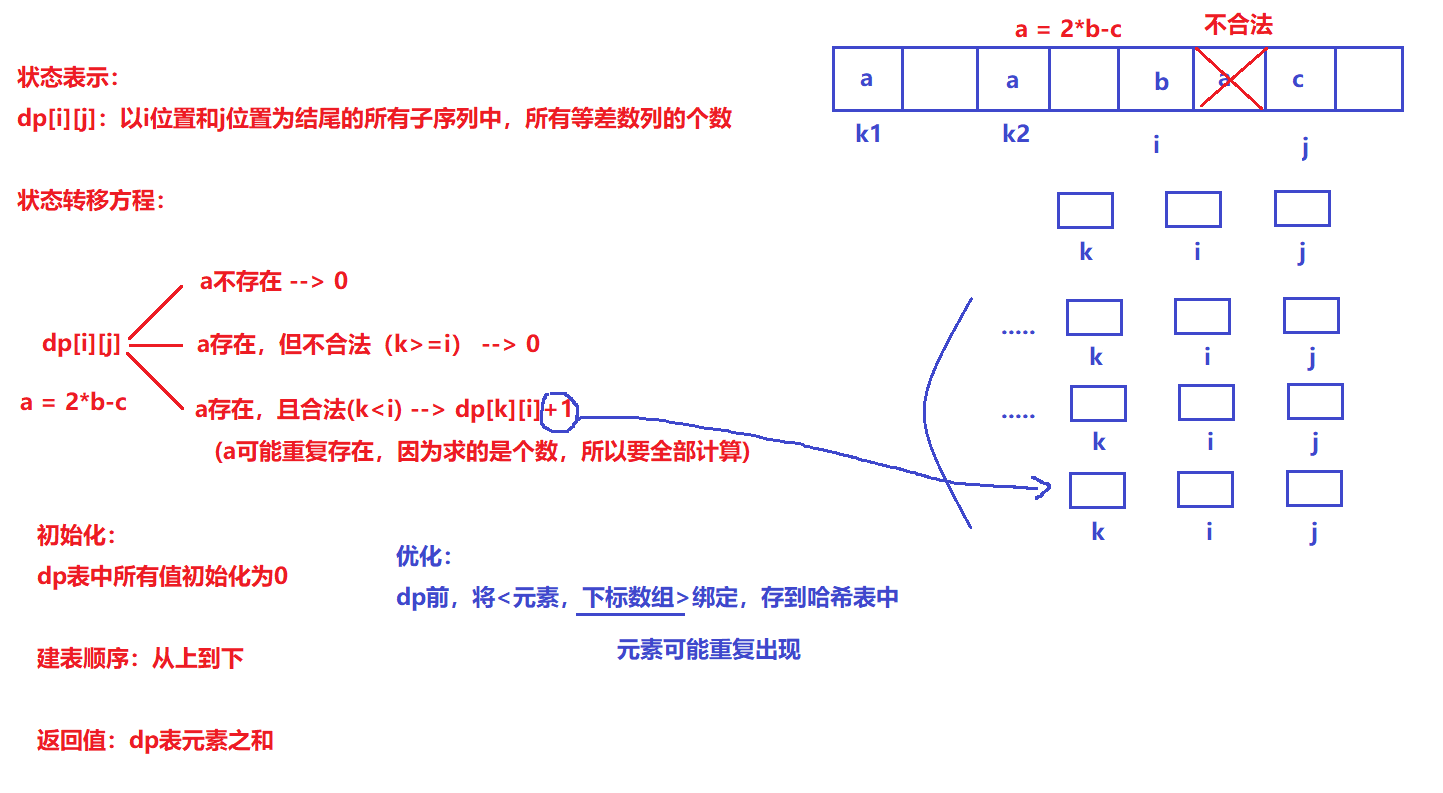
dp[i][j]:以i位置和j位置为结尾的所有子序列中,所有等差数列的个数
- 状态转移方程:
a = 2*b-c
1. a不存在 --> dp[i][j] = 0
2. a存在,但不合法(k>=i) --> dp[i][j] = 0
3. a存在,且合法(k<i) --> dp[i][j] += dp[k][i]+1;(a可能重复存在,因为求的是个数,所以要全部计算)
- 初始化:
dp表中所有值初始化为0
- 建表顺序:
从上到下
- 返回值:
dp表元素之和
优化:
dp前,将<元素,下标数组>绑定,存到哈希表中
8.2 算法代码
class Solution {
public int numberOfArithmeticSlices(int[] nums) {
int n = nums.length;
int[][] dp = new int[n][n];
// <元素, 下标数组>
// Long --> 防溢出
Map<Long, List<Integer>> hash = new HashMap<>();
for(int i = 0; i < n; i++) {
List<Integer> list = hash.getOrDefault((long)nums[i], null);
if(list != null) {
list.add(i);
}else {
hash.put((long)nums[i], new ArrayList<>());
hash.get((long)nums[i]).add(i);
}
}
int ret = 0;
for(int i = 1; i < n; i++) { // 固定倒数第二个数
for(int j = i + 1; j < n; j++) { // 枚举倒数第一个数
long val = 2L * nums[i] - nums[j]; // 找第一个数
List<Integer> list = hash.getOrDefault(val, null);
if(list != null) {
int sum = 0;
for(int x : list) {
if(x < i) sum += dp[x][i] + 1;
}
dp[i][j] = sum;
ret += sum;
}
}
}
return ret;
}
}END