反思
新手小白学算法时的题记。本文都是个人的见解,如有疑惑的地方欢迎评论,小白会改进的。
问题:做一道有线段重叠的问题时,一直报TLE。
反映的情况:
(1)对时间复杂度不够理解,也不怎么关注时间复杂度,导致常常报TLE的错误。
(2)对于前缀和、差分算法掌握不牢,没能深刻明白差分的应用。
(3)缺少合并区间这种更新左右端点的思想。
一、线段重叠问题
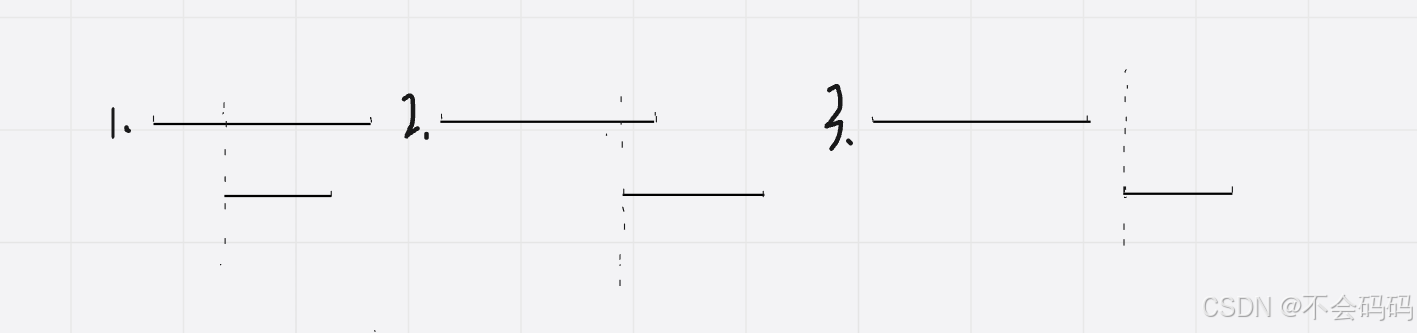
两段线段有2种分布情况:
(1)两条线段有重叠部分(完全重叠、部分重叠)
(2)两条线段相离
二、例题
1.又下雨了
题目描述
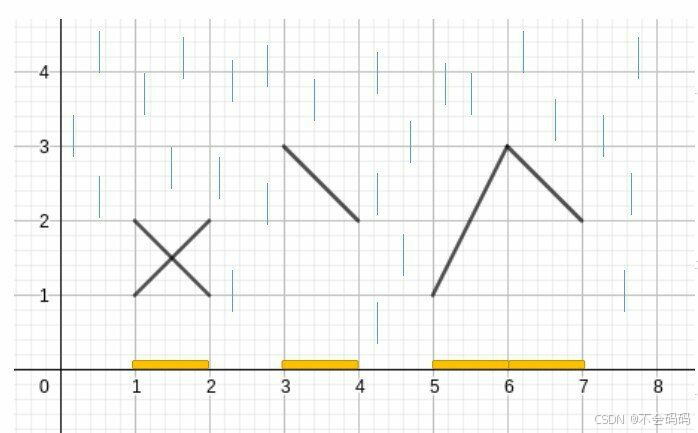
假设在无限平面上的直角坐标系中,X 轴代表地面,天空中有 n 块雨布(我们不考虑它们的厚度)。 每块雨幕都可以描述为一个线段,它从(x1,y1)开始,到 (x2,y2) 结束。现在,如果从无限高的天空开始下雨,我想让你告诉我 x 轴上有多少个单位不会被雨淋到。
为了简化问题,雨水落下时只能垂直移动。 请注意,两块雨幕可以相互重叠和交叉,而且没有垂直放置的雨幕。输入
第一行包含一个正整数 n(1≤n≤100000)。 接下来的 n 行中,每一行都包含四个正整数
x1,y1,x2,y2(1≤x1<x2≤100000,1≤y1,y2≤100000),代表一个从 (x1,y1)开始到
(x2,y2)结束的雨幕。输出
唯一的整数 - 不会被雨淋到的 x 轴单位数。Example
input
5
1 2 2 1
1 1 2 2
3 3 4 3
5 1 6 3
6 3 7 2
output
4
题意:
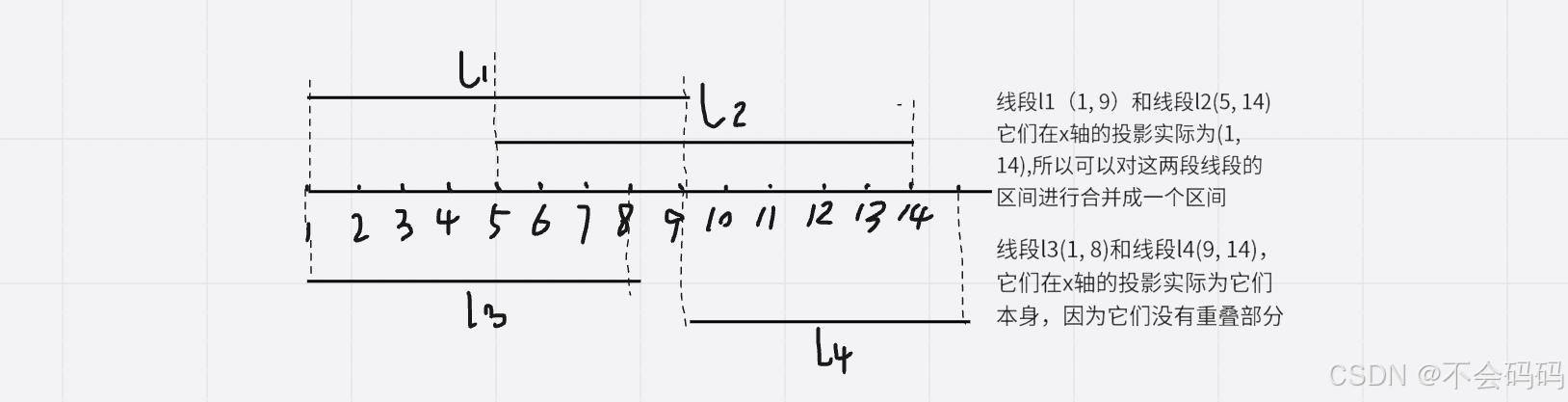
输入线段的表示:(x1, y1),(x2, y2),其对应x轴方向上的投影线段:(x1, x2)。
题目要求输入的各线段在x轴投影的线段长度总和,注意这些线段在x轴上的重叠部分。因为只涉及到x轴方向上投影的线段长度,不用考虑y轴的情况。
1.排序
思路
合并各个投影线段的重复区间(合并区间),累加处理后的区间长度就是要求的答案。
实现步骤
第一步:存储输入的各线段的投影线段,也就是(x1, x2)。
存储方式用二维数组,每个一维数组两个元素,分别存储x1, x2。如此例子:
vector<vector<int>> a(n, vector<int>(2, 0));
for(int i = 0; i < n; i++) {// 第一步:存储数据
cin >> x1 >> y1 >> x2 >> y2;
a[i][0] = x1;
a[i][1] = x2;
}
第二步:对数组a进行排序(左端点升序排序)
方便我们按从左到右的顺序进行合并区间操作
sort(a.begin(), a.end());// 第二步:左端点进行排序
第三步:合并区间,这样可以消去重叠区间的影响(在排序的基础上)
就着线段重叠情况来分析:
第一种情况:两线段有重叠部分
判断条件:第二条线段的左端点小于等于第一条线段的右端点,则两线段有重叠部分。
更新操作:将第二条线段的左端点更新为第一条线段的左端点,第二条线段的右端点更新为这两条线段右端点更大的一个。
第二种情况:两线段没有重叠部分,不用进行更新操作。
for(int i = 1; i < n; i++) {
if(a[i][0] <= a[i - 1][1]) {// 第三步:线段重叠处理
a[i][0] = a[i - 1][0];
a[i][1] = max(a[i][1], a[i -1][1]);
a[i - 1][0] = 0;// 注意:把原本的线段归0,因为当前的a[i]已经包含了当前线段和原本的线段
a[i - 1][1] = 0;
}
}
第四步:累加区间长度
for(int i = 0; i < n; i++) {// 第四步:累加区间长度
ans += a[i][1] - a[i][0];
}
完整代码实现:
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
using ll = long long;
const int mod = 998244353;
int x, y, x2, y2, ans = 0;
void solve() {
int n;
cin >> n;
vector<vector<int>> a(n, vector<int>(2, 0));
for(int i = 0; i < n; i++) {// 第一步:存储数据
cin >> x >> y >> x2 >> y2;
a[i][0] = x;
a[i][1] = x2;
}
sort(a.begin(), a.end());// 第二步:左端点进行排序
for(int i = 1; i < n; i++) {
if(a[i][0] <= a[i - 1][1]) {// 第三步:线段重叠处理
a[i][0] = a[i - 1][0];
a[i][1] = max(a[i][1], a[i -1][1]);
a[i - 1][0] = 0;// 注意:把原本的线段归0,因为当前的a[i]已经包含了当前线段和原本的线段
a[i - 1][1] = 0;
}
}
for(int i = 0; i < n; i++) {// 第四步:累加区间长度
ans += a[i][1] - a[i][0];
}
cout << ans << endl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(nullptr);
int t = 1;
//cin >> t;
while(t--) {
solve();
}
return 0;
}
2.前缀和、差分
1.知识点回顾
1.前缀和
示例:
前缀和,字面意思就是前面元素的累加。
sums[i]:表示索引i以及索引i以前的元素之和。
问题:
给你n个整数,再给你t个询问,每次询问给出区间[l, r],快速求出由这n个数组成的数组区间为[l,r]的元素之和。
(1)前缀和解
时间复杂度为O(t + n)
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(0); cin.tie(nullptr);
int n, t;
cin >> t >> n;
vector<int> nums(n, 0);
vector<int> sums(n, 0);
for(int i = 0; i < n; i++) {
cin >> nums[i];
if(i) {// 当i不为0时,0 - 1为负
sums[i] = sums[i - 1] + nums[i];
} else {// 相当于 sums[0] = nums[0];
sums[i] = nums[i];
}
}
while(t--) {// t次询问
int l, r;
cin >> l >> r;
if(l) {// 注意:l为0时,直接输出sums[r]
cout << sums[r] - sums[l - 1] << endl;
} else {
cout << sums[r] << endl;
}
}
return 0;
}
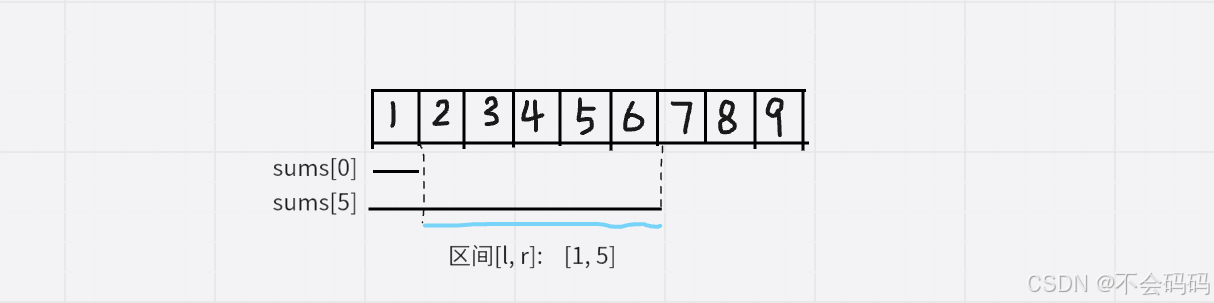
1.区间[l, r]之间和元素和怎么用前缀和来表示?
2.为什么求区间[l, r]元素的和,是sums[r] - sums[l - 1]而不是sums[r] - sums[l]?
首先我们要清楚sums[i]表示的含义:索引i以及i之前的元素之和。区间[l, r]之间的元素之和,包含两个端点元素,如果是sums[r] - sums[l],那么nums[l]就会被减去,从而错误。
(2) 暴力解法
时间复杂度为O(t * n)
#include <bits/stdc++.h>
using namespace std;
vector<int> nums = {1, 2, 3, 4, 5};
void solve(int l, int r) {
int ans = 0;
for(int i = l; i <= r; i++) {
ans += nums[i];
}
cout << ans << endl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(nullptr);
int t;
cin >> t;
while(t--) {// t次询问
int l, r;
cin >> l >> r;
solve(l, r);
}
return 0;
}
比较这两种方法,暴力算法时间复杂度比较高,容易TLE,而前缀和求区间长度相比之下就是更优解了。
2.差分
定义:
序列a的差分序列b定义为:
b[1] = a[1];// 初始化
b[i] = a[i] - a[i - 1];
b[i]表示:元素a[i]与它前一个元素a[i - 1]的差值。
b序列是a序列的差分,a序列是b序列的前缀和。
tip:
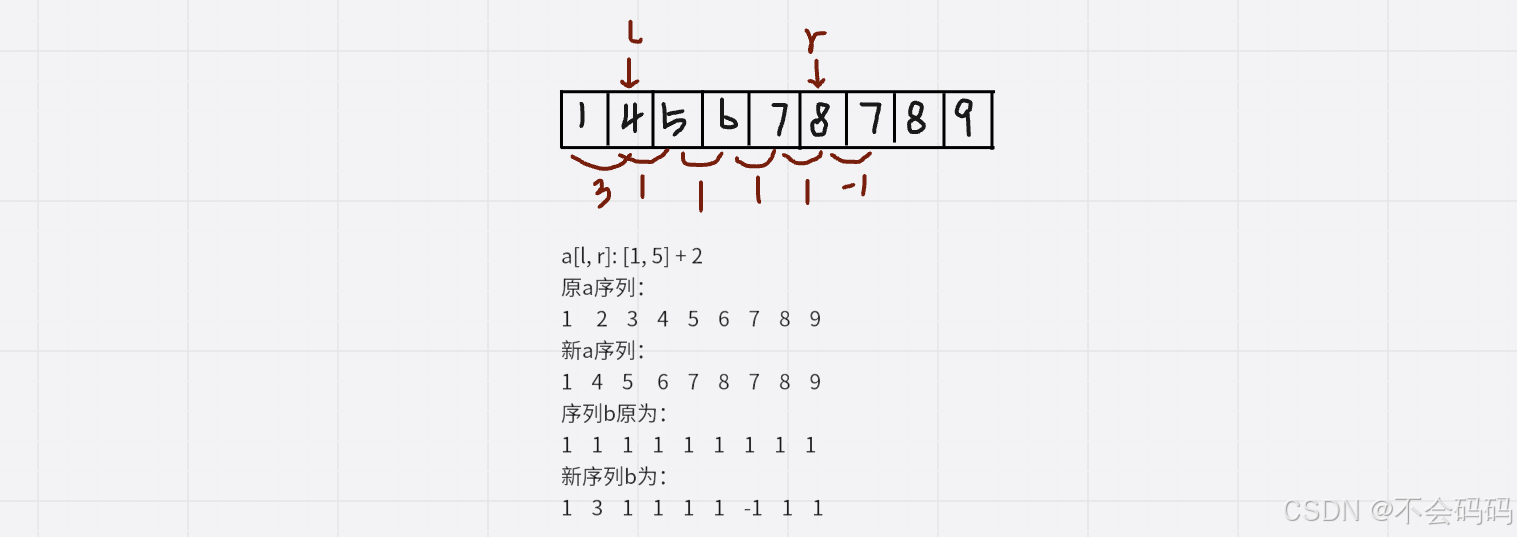
给序列a区间为[l, r]的元素都加上d,等价于b[l] + d, b[r + 1] + d,那么区间操作可以转换为两点操作(优化)。
分析:
由于是区间[l,r]的元素都加上相同的d,那么这些元素之间的差分是不变的,所以我们要特别关注区间端点处的差分就可以了。
b[i]的含义:
nums[i]与前面一个元素nums[i - 1]的差值
在进行nums[1, r] + d的操作后:
b[l] = nums[l] + d - nums[l - 1] = nums[l] - nums[l - 1] + d;// 原本的b[l] + d
b[r] = nums[r] + d -( nums[r - 1] +d) = nums[r] - nums[r - 1];// 也就是原本的b[r]
b[r + 1] = nums[r + 1] - (nums[r] + d) = b[r + 1] - d;// 原本的b[r + 1] - d;
很明显,差分与原来的相比,在b[l],b[r + 1]处有改变
总结:
序列a的区间[l, r]加d后,相当于b[l] + d, b[r + 1] - d。
2.前缀和、差分解题
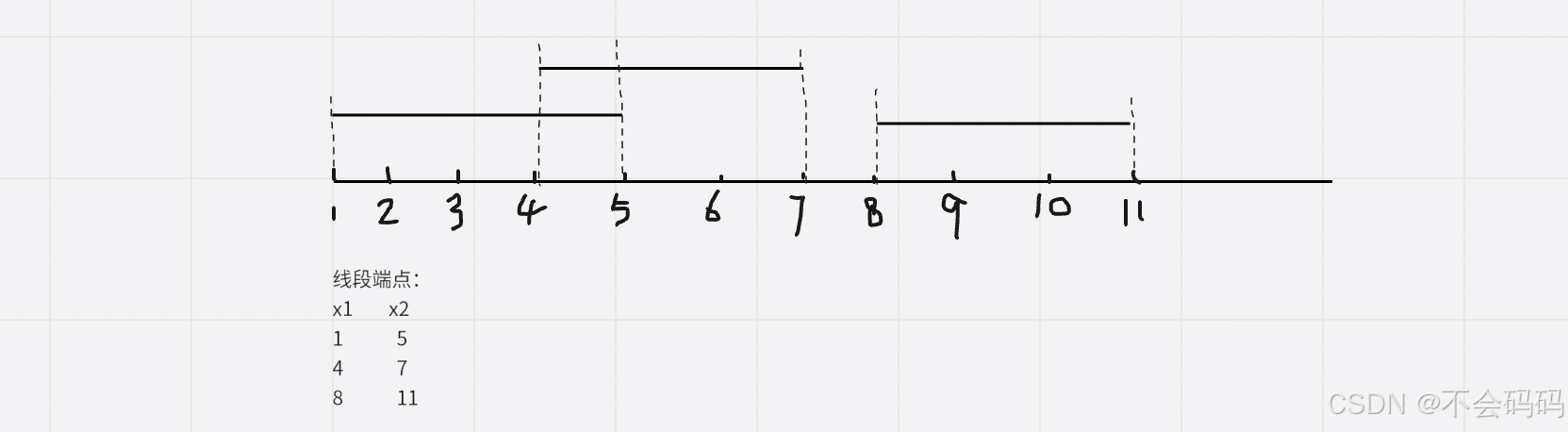
用差分表示线段的长度:
想到用差分是因为:可以用差分并还原来标记一段线段表示点的覆盖情况,例如:
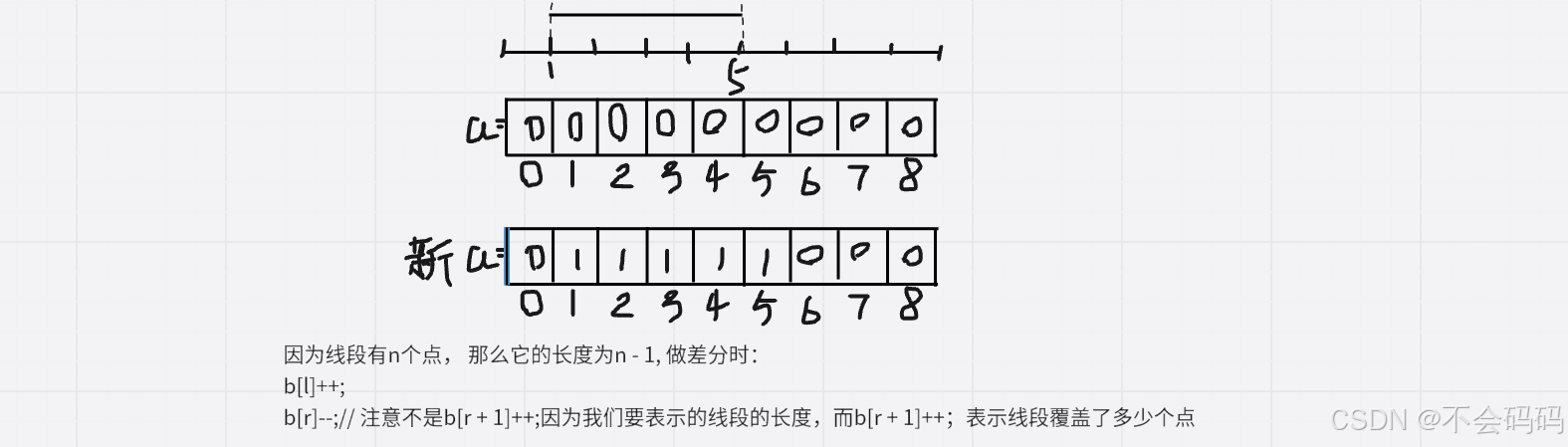
如果想要标记线段(1,5),可以通过差分来表示:
b[1]++;
b[5 + 1]–;
这样还原序列a后,变为:
for(int i = 0; i < n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
a[x1]++;
a[x2]--;
mx = max(mx, x2);
}
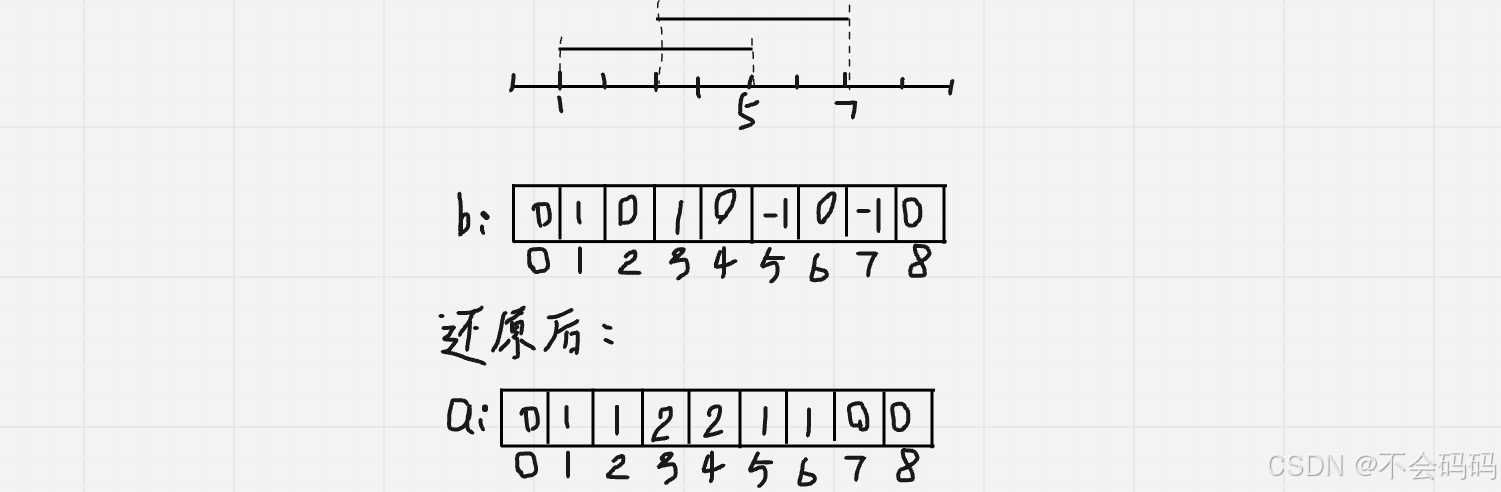
累加区段长:
可以发现,覆盖的点在相应的a[i]是相加了,但是我们只需要计算其中非0元素的个数就能得到答案了。因为覆盖的点比如图中的2,表示有两条线段覆盖了该点,但是我们只需要判断该点是否被覆盖,也就是判断a[i]是否为1,为1,就长度加1,否则就不加。
代码实现:
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
using ll = long long;
const int mod = 998244353;
const int N = 100005;
int a[N];
void solve() {
int n;
cin >> n;
int mx = 0;
for(int i = 0; i < n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
a[x1]++;
a[x2]--;
mx = max(mx, x2);
}
int ans = 0;
for(int i = 0; i <= mx; i++) {
if(i) {
a[i] += a[i - 1];
}
if(a[i]) {
ans++;
}
}
cout << ans << endl;
}
int main() {
ios::sync_with_stdio(0); cin.tie(nullptr);
int t = 1;
//cin >> t;
while(t--) {
solve();
}
return 0;
}
2.用最少数量的箭引爆气球
题目连接:452. 用最少数量的箭引爆气球
题目描述
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart,xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend,且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。给你一个数组 points ,返回引爆所有气球所必须射出的 最小弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:气球可以用2支箭来爆破:
在x = 6处射出箭,击破气球[2,8]和[1,6]。
在x = 11处发射箭,击破气球[10,16]和[7,12]。 示例 2:输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
解释:每个气球需要射出一支箭,总共需要4支箭。
示例 3:输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2 解释:气球可以用2支箭来爆破:
- 在x = 2处发射箭,击破气球[1,2]和[2,3]。
- 在x = 4处射出箭,击破气球[3,4]和[4,5]。
提示:
1 <= points.length <= 10^5
points[i].length == 2
-2^31 <= xstart < xend <= 2^31 - 1
题意:用最少的弓箭射击气球,贪心,每次用一根弓箭击穿最多能击穿的气球,这就涉及到线段重复问题,因为气球会有重叠的。为了方便我们对重复区间进行操作,要先排序。
贪心 + 排序
射击的情况:
(1)当前气球下侧没有气球时,进行射击。
(2)当前气球下侧有气球时,继续往下面找寻是否还有气球在它的下侧,直到气球下侧没有气球,进行射击。
代码实现:
int findMinArrowShots(vector<vector<int>>& points) {
int len = points.size();
if(len == 0) {
return 0;
}
int ans = 1;
sort(points.begin(), points.end());
for(int i = 1; i < len; i++) {
if(points[i][0] > points[i - 1][1]) {
ans++;
} else {// 关键点
points[i][1] = min(points[i][1], points[i - 1][1]);
}
}
return ans;
}
3.合并区间
题目连接:Leetcode 56. 合并区间
题目描述
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi]
。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。提示:
1 <= intervals.length <= 104 intervals[i].length == 2 0 <= starti <=
endi <= 104
分析:对重叠的区间进行一个更新操作,使之不在有重叠的区间。
vector<vector<int>> merge(vector<vector<int>>& intervals) {
int len = intervals.size();
if(len == 1) {
return intervals;
}
vector<vector<int>> merged;
sort(intervals.begin(), intervals.end());
for(int i = 0; i < len; i++) {
if(!merged.size() || merged.back()[1] < intervals[i][0]) {
merged.push_back(intervals[i]);
} else {// 关键点
merged.back()[1] = max(merged.back()[1], intervals[i][1]);
}
}
return merged;
}
总结
本文主要介绍了关于线段或者区间重叠的问题,涉及到求重叠线段的总长度,合并区间等操作。