2024年最全数据结构堆的向上调整和向下调整算法【奇妙的堆排序】(3)，血与泪的总结

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

首先可以来看下代码，可以看到很显目的一句，就是交换【a[0]】和【a[hp->size - 1]】，这其实值的就是堆顶的结点和堆顶的末梢结点，为什么先要交换它们呢，我们来分析一下

/\*堆的删除\*/
void HeapPop(Hp\* hp)
{
	assert(hp);
	assert(hp->size > 0);
	//首先交换堆顶和树的最后一个结点 —— 易于删除数据，保护堆的结构不被破坏
	swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;		//去除最后一个数据

	Adjust\_Down(hp->a, hp->size, 0);
}

改写族谱，关系紊乱😵

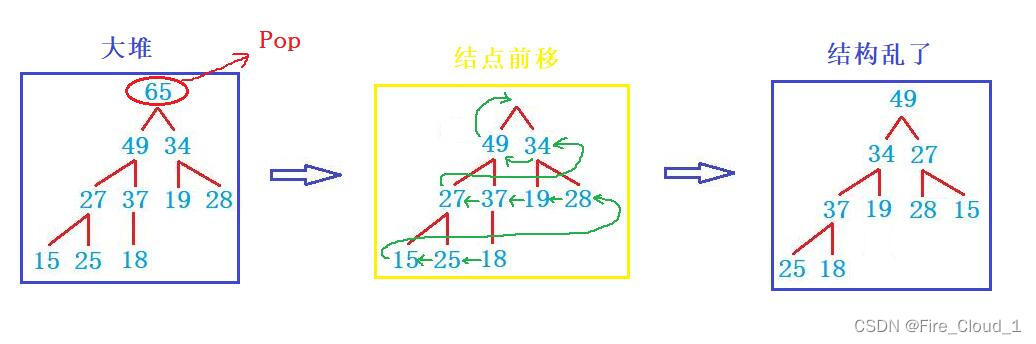
若是我们什么都不做，直接去删除一下这个堆顶的数据，后面的结点就需要前移，此时的原本的孩子结点就会变成父亲，父亲呢可能又会变成孩子。这其实也就乱了，是吧，原本呢【49】和【34】说我们要做一辈子的好兄弟，但是呢当它们的爸爸没了之后，【49】就想要当上爸爸。原本的【27】是【34】的远方亲戚，但是呢现在却成了兄弟，所以心疼【34】3秒钟🦌🦌🦌
所以说直接去删除这个堆顶的数据一定不行，会对整个堆造成一定的影响，那我们该怎么办呢❓
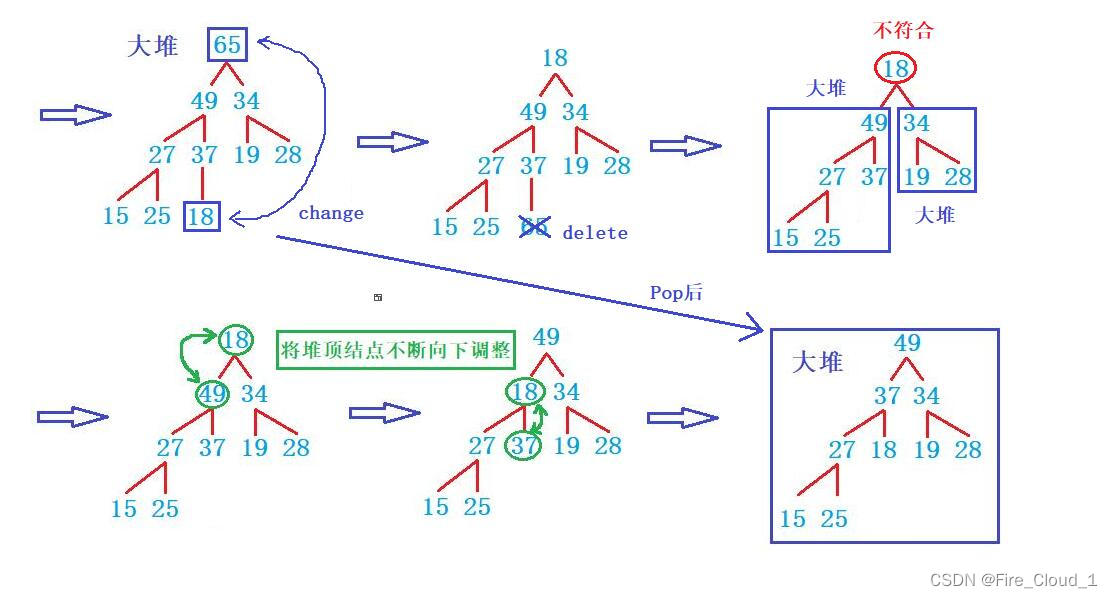
此时就像代码中写的一样，我们可以先去交换一下堆顶和堆底末梢的数据，然后将交换下来的数删除，这样既可以删除这个堆顶的数据，也不会影响整棵树的结构，整体算法图如下

在这里插入图片描述

通过这组算法图我们可以看出，堆顶数据不符合，但是其左右子树均符合大堆或者是小堆的时候，此时我们就可以去进行一个【向下调整算法】，这个过程就是我上面分析过的，一直调整到其孩子结点为n的时候就表明其孩子不存在了，就无需再向下进行调整
可以看到，在Pop完数据进行向下调整后，依旧是保持一个大堆

5、取堆顶的数据

这块很简单，因为堆顶的数据就是数组的首元素，因此直接return【hp->a[0]】即可

/\*取堆顶数据\*/
HpDataType HeapTop(Hp\* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->a[0];
}

上面说到过，结构体中的【size】是指向当前堆底末梢数据的后一个位置，也就相当于【n】，因此求数据个数直接return【hp->size】即可

6、堆的数据个数

/\*返回堆的大小\*/
size_t HeapSize(Hp\* hp)
{
	assert(hp);
	return hp->size;
}

7、堆的判空

堆的判空就是当数据个数为0的时候

/\*判断堆是否为空\*/
bool HeapEmpty(Hp\* hp)
{
	assert(hp);
	return hp->size == 0;
}

8、堆的构建

对于堆的创建这一块，有两种方法，一种是直接利用我们上面所写的【Init】和【Push】联合向上调整建堆；另一种则是利用数据拷贝进行向下调整建堆

Way1

首先我们来看第一种。很简单，就是利用【Init】和【Push】联合向上调整进行建堆

/\*建堆\*/
void HeapCreate1(Hp\* hp, HpDataType\* a, int n)
{
	assert(hp);
	HeapInit(hp);
	for (int i = 0; i < n; ++i)
	{
		HeapPush(hp, a[i]);
	}
}

Way2√

接着是第二种，比较复杂一些，不会像【向上调整算法】一样插入一个调整一个，而是为这个堆的存放数据的地方单独开辟出一块空间，然后将数组中的内容拷贝过来，这里使用到了memcpy，不懂的小伙伴可以先去了解一下它的用法
当把这些数据都拿过来之后，我们去整体性地做一个调整，那就不可以做向上调整了，需要去进行一个【向下调整】，我们通过图解来看看

HeapInit(hp);
HpDataType\* tmp = (HpDataType\*)malloc(sizeof(HpDataType) \* n);	//首先申请n个空间用来存放原来的堆
if (tmp == NULL)
{
	perror("fail malloc");
	exit(-1);
}
hp->a = tmp;

//void \* memcpy ( void \* destination, const void \* source, size\_t num );
memcpy(hp->a, a, sizeof(HpDataType) \* n);	//将数组a中n个数据拷贝到堆中的数组
hp->size = n;
hp->capacity = n;

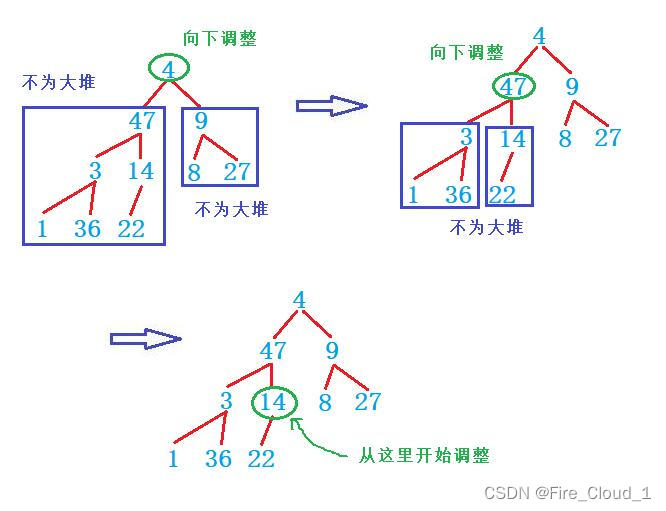
在这里插入图片描述

可以看到，对于即将要调整的根结点，首先我们要回忆一下向下调整算法的先决条件，就是当要调整的结点的左右子树均为大堆或者小堆，只有待调整的结点不满足时，才可以使用这个算法，但是可以看到，【4】下面的两个子树均不是大堆（我这里默认建大堆），那有同学说这该怎么办呢？此时我们应该先去调整其左右子树，使他们先符合条件才行
然后可以看到左子树这一边，当【47】作为要调整的结点时，它的左右子树依旧不是一个大堆，此时我们需要做的就是再去调整其左右子树，直到其符合条件为止，那此时我们应该去调整【3】【14】，那还需要再去调整其左右子树吗？可以看到【1】和【36】确实也是不符合，但是呢对于叶子结点来说是没有孩子的，所以调不调整都一个样，因此我们只需要从倒数第二层开始调整就行，也就是最后一个非叶子结点，即【14】
那要如何去找到和这个【14】呢，这个好办，我们可以知道它的孩子，就是堆底的末梢元素，那对于数组来说最后一个数据的下标为【n - 1】，在上面有说到过已知孩子结点去求结点其父亲结点【(child - 1)/2】，那这里的【child】我们使用【n - 1】带入即可，然后通过循环来一直进行调整，但是在调整完【14】这棵子树后要怎么越位到【3】这棵子树呢，上面说到了，堆存放在一个数组中，因此我们直接将这个【parent - 1】就可以继续往前调整了。最后直到根节点为止就是我们上面讲解【向下调整算法】时的样子

//向下调整 
/\*
\* （n - 1）代表取到数组最后一个数据，不可以访问n
\* (x - 1)/2 代表通过孩子找父亲
\*/
for (int i = ((n - 1) - 1) / 2; i >= 0; --i)
{
	Adjust\_Down(hp->a, n, i);
}

下面是【向下调整算法建堆】执行的全过程

测试💻

说了这么多，还不知道写得代码到底对不对，我们来测试一下

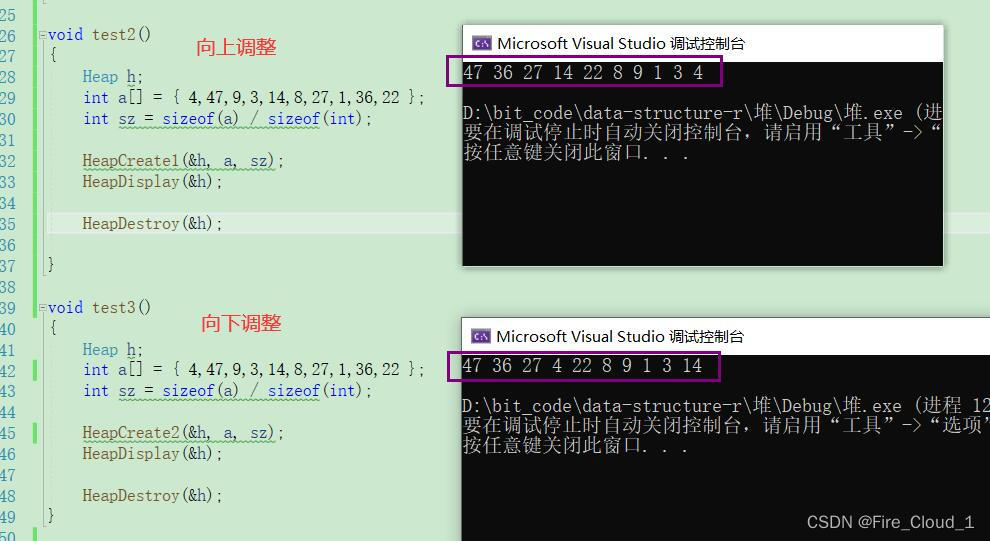
首先的话是基本的接口功能测试

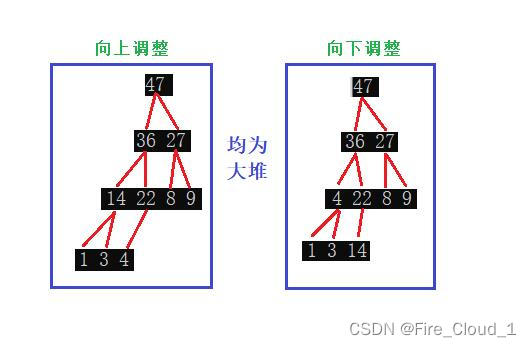
然后把向上建堆和向下建堆一起看，好作辨析。

可以看到，均可以完成建堆的操作

在这里插入图片描述

五、两种调整算法的复杂度精准剖析⏳

开头讲了两种堆的调整算法，分别是【向上调整】和【向下调整】，在接口算法实现Push和Pop的时候又用到了它们，以及在建堆这一块我也对它们分别做了一个分析，所以我们本文的核心就是围绕这两个调整算法来的，但是它们两个到底谁更加优一些呢❓
这里就不做过多解释，直接看图即可

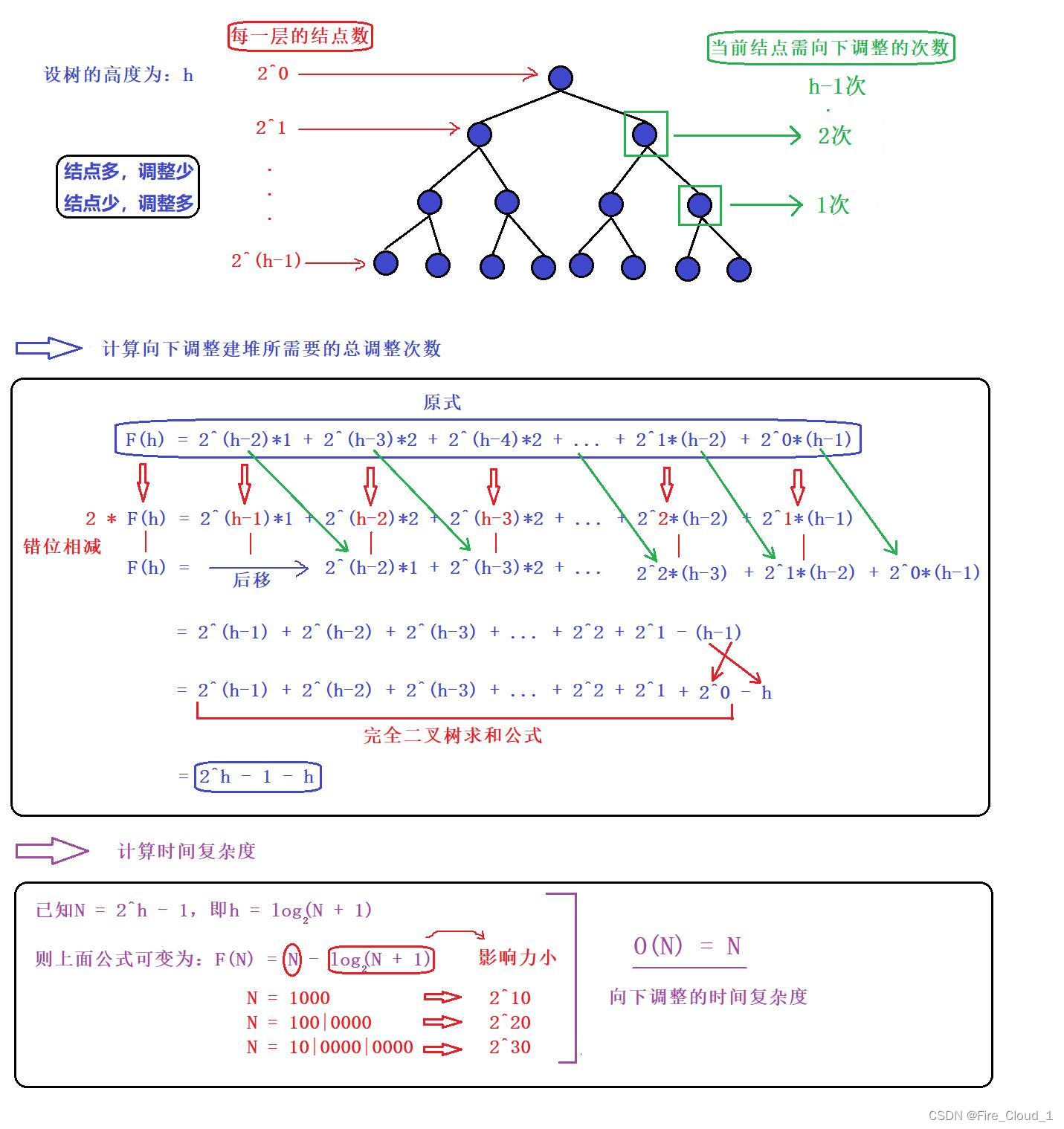
1、向下调整算法【重点掌握】

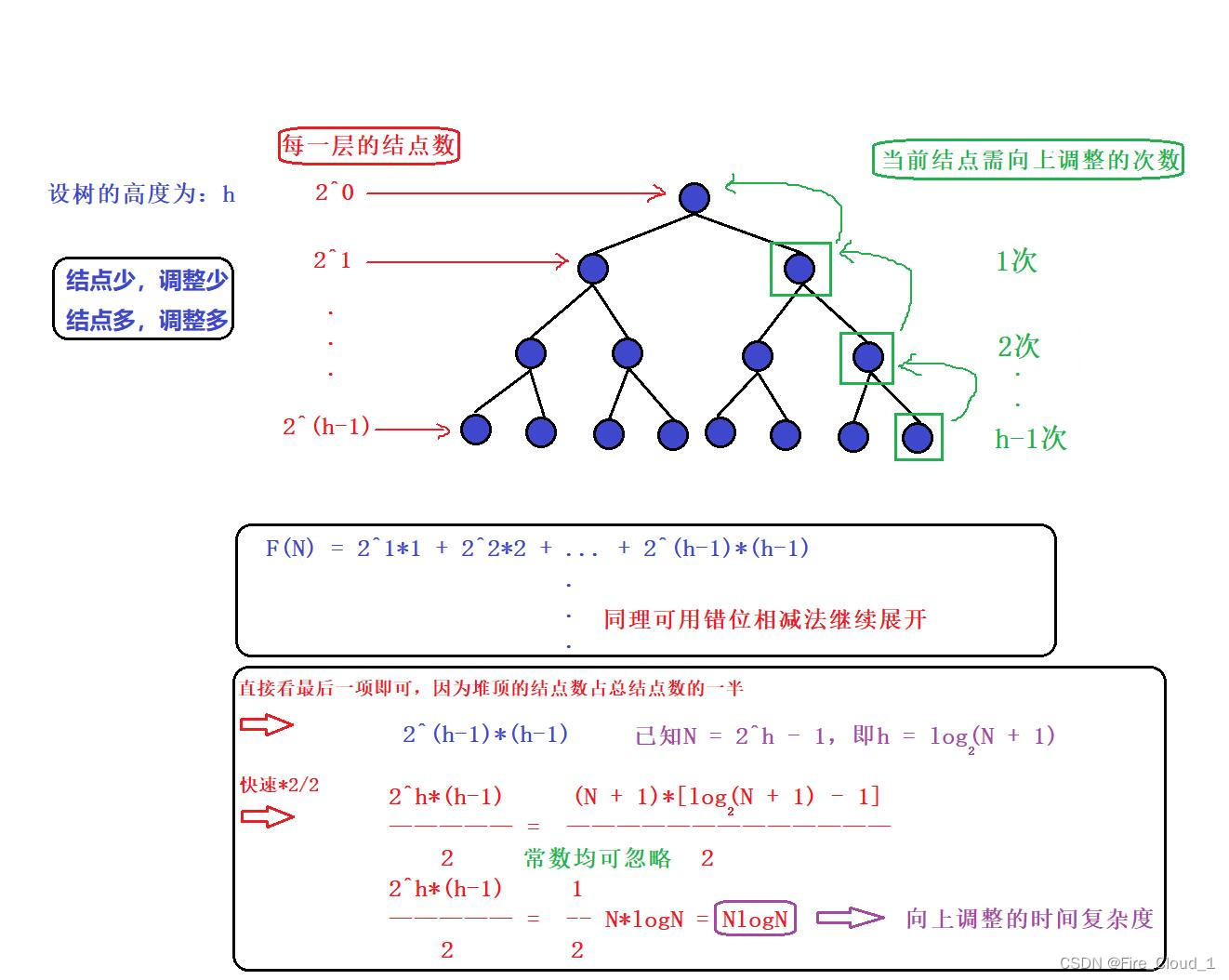
2、向上调整算法

好，我们来总结一下，对于【向上调整算法】，它的时间复杂度为O(NlogN)；对于【向下调整算法】，它的时间复杂度为O(N)
很明显，【向下调整算法】来得更优一些，因为向下调整随着堆的层数增加结点数也会变多，可是结点越多调整得就越少，因为在一些大型数据处理场合我们会使用向下调整
当然在下面要讲的堆排序中我们建堆也是利用的向下调整算法，所以大家重点掌握一个就行

六、堆的实际应用

1、堆排序【⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐】

讲了那么久的堆，学习了两种调整算法以及它们的时间复杂度分析，接下去我们来说说一种基于堆的排序算法——【堆排序】

升序建大堆 or 小堆❓

在上面解说的时候，我建立的默认都是大堆，但是在这里我们要考虑排序问题了，现在面临的是【升序】，对于升序就是数组前面的元素小，后面的元素大，这个堆也是基于数组建立的，那就是要堆顶小，堆顶大,很明显就是建【小堆】
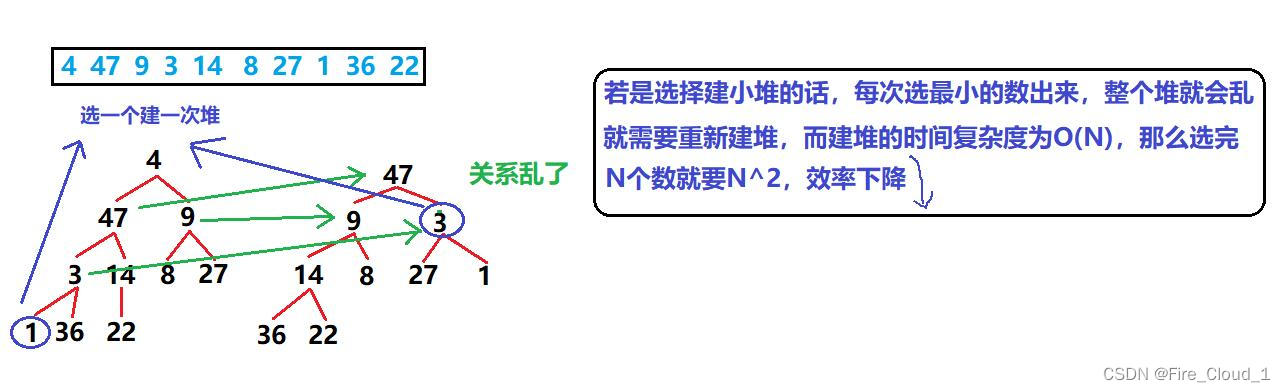
一波分析猛如虎🐅，我们通过画图来分析是否可以建【小堆】

在这里插入图片描述

可以看到，对于建小堆来说，原本的左孩子结点就会变成新的根结点，而右孩子结点就会变成新的左孩子结点，整个堆会乱，而且效率并不是很高，因此我们应该反一下，去建大堆

//建立大根堆（倒数第一个非叶子结点）
for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
{
	Adjust\_Down(a, n, i);
}

如何进一步实现排序❓

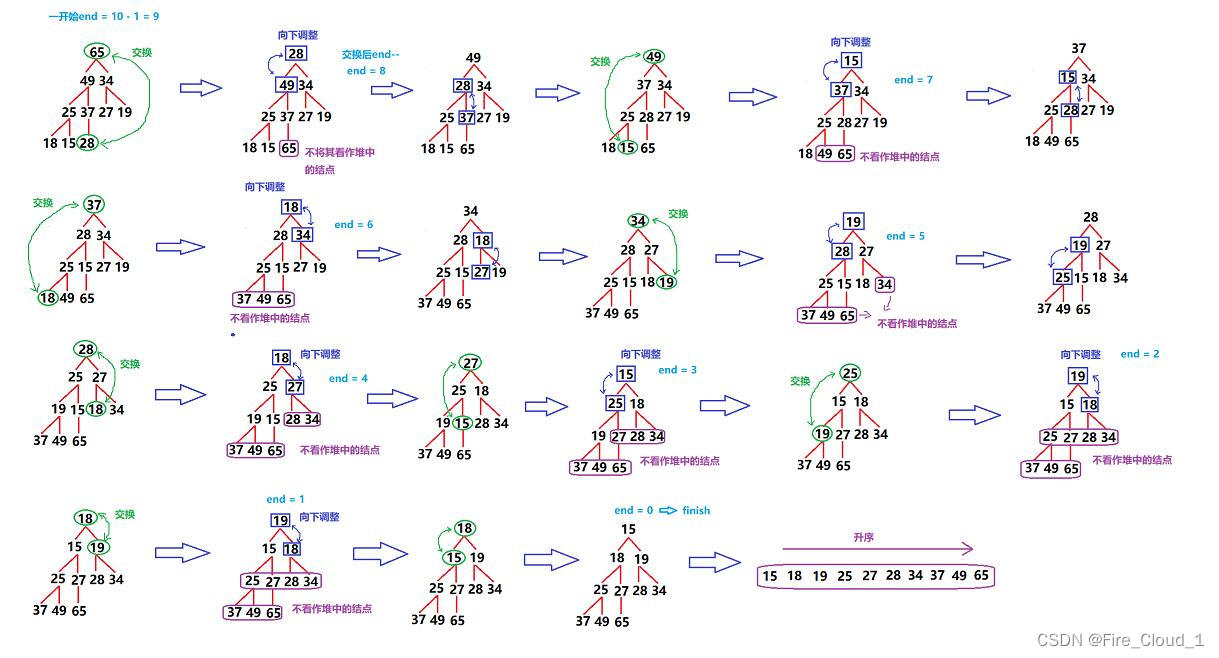
有了一个大堆之后，如何去进一步实现升序呢，这里就要使用到我上面在Pop堆顶数据的思路了，也就是现将堆顶数据与堆底末梢数据做一个交换，然后对这个堆顶数据进行一个向下调整，将大的数往上调。具体过程如下

在这里插入图片描述

对照代码，好好分析一下堆排的全过程吧

/\*堆排序\*/
void HeapSort(int\* a, int n)
{
	//建立大根堆（倒数第一个非叶子结点）
	for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
	{
		Adjust\_Down(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);		//首先交换堆顶结点和堆底末梢结点
		Adjust\_Down(a, end, 0);		//一一向前调整
		end--;
	}
}

看一下时间复杂度，建堆这一块是O(N)，调整这一块的话就是每次够把当前堆中最的数放到堆底来，然后每一个次大的数都需要向下调整O(log2N)，数组中有N个数需要调整做排序，因而就是O(Nlog2N)。
当然你可以这么去看：第一次放最大的数，第二次是次大的数，这其实和我们上面讲过的向上调整差不多了，【结点越少，调整越少；结点越多，调整越多】，因此它也可以使用之前我们分析过的使用的【错位相减法】去进行求解，算出来也是一个O(Nlog2N)。
最后将两段代码整合一下，就是O(N + Nlog2N)，取影响结果大的那一个就是O(Nlog2N)，这也就是堆排序最终的时间复杂度

2、Top-K问题

对堆这一块还有一个经典的问题就是Top - K：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。

复杂度分析

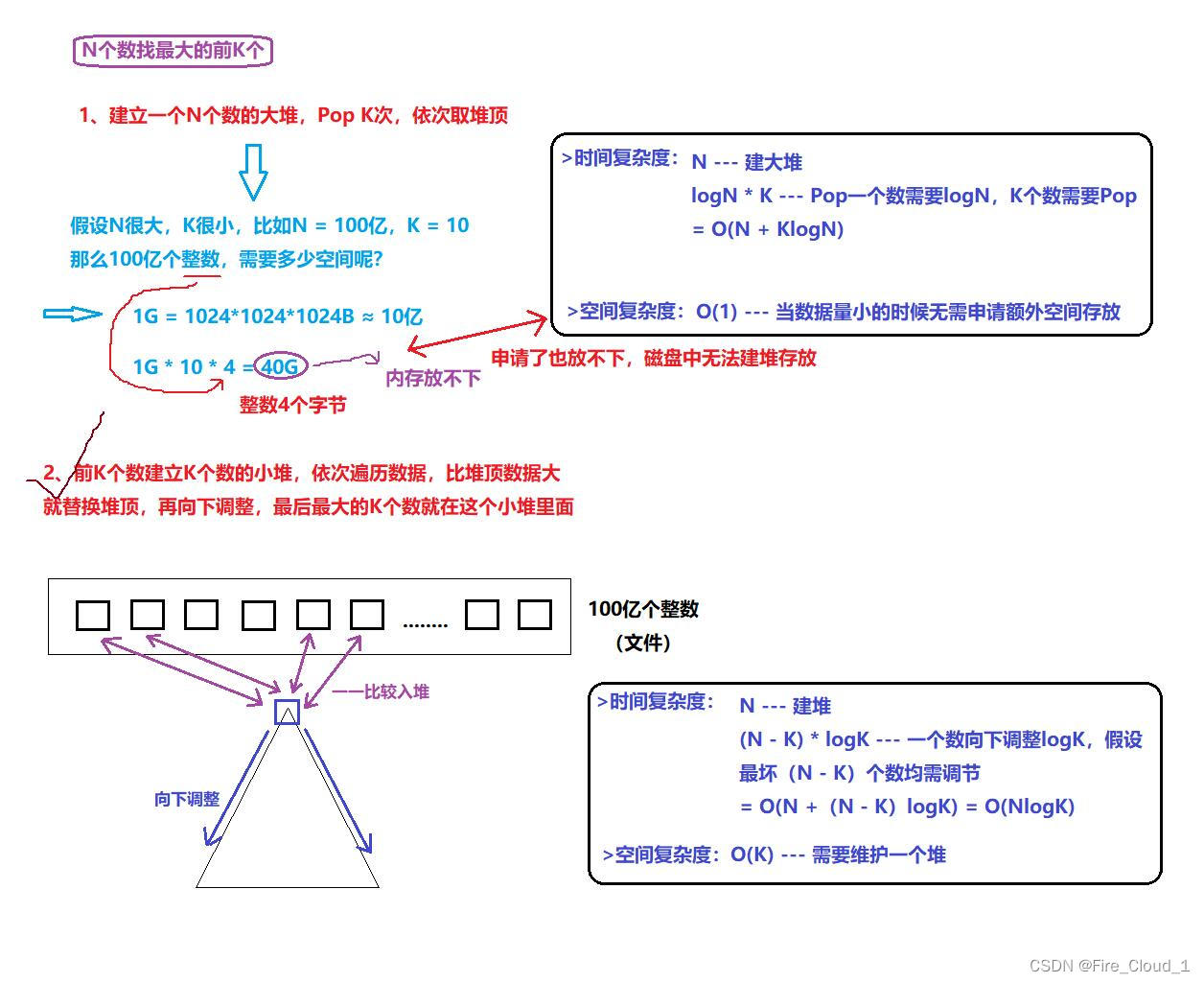
现在假设我要在N个数中找前K个最大的数字，那你会采用什么样的方法去求解呢？要结合我们所学习的【堆】

代码详情

经过分析之后呢我们就选择了第二种方式建堆去进行求解前K个最大的数。下面是代码
在这里我使用到了从文件中读出数据的方法，要结合C语言中的【文件操作】，若是忘记的小伙伴可以去回顾一下。以下代码的具体思路就是：通过一个文件指针首先去访问到这个文件，首先读出k个数放入数组中，有了这个k个数以后，我们就要先去建立一个堆，这里记住要建【小堆】，接着继续去读取剩下的数字，将每次读取的数组与堆顶的数进行一个比较，若是比堆顶的数要来的大，那么就进行一个替换，然后对这个新进来的数进行一个向下调整，保持这个堆依旧还是一个【小堆】。一直这么循环往复，直到文件中的数读取完毕，然后输出数组中的所有数就是我们维护的堆中的前K个最大的数

/\*TopK\*/
void HeapTopK()
{
	//1.使用一个文件指针指向这个文件
	FILE\* fout = fopen("data.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

	//2.读出前k个数放入数组中
	int k = 5;
	int max[5];
	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &max[i]);
	}

	//3.建立k个堆
	for (int i = ((k - 1) - 1) / 2; i >= 0; --i)
	{
		Adjust\_Down(max, k, i);
	}

	//4.继续读取剩下的数据
	/\*
 \* 不断和堆顶数据做比较，比堆顶大就入堆，然后继续向下调整
 \*/
	int val = 0;
	while ((fscanf(fout, "%d", &val)) != EOF)		//不停读取剩下的数据
	{
		if (val > max[0])
		{
			max[0] = val;		//替换为堆顶
			Adjust\_Down(max, k, 0);		//将其做向下调整
		}
	}

	//5.打印数组中的数据，观看TopK个最大的数
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", max[i]);
	}
	printf("\n");
	fclose(fout);
}

我们来看一下运行结果

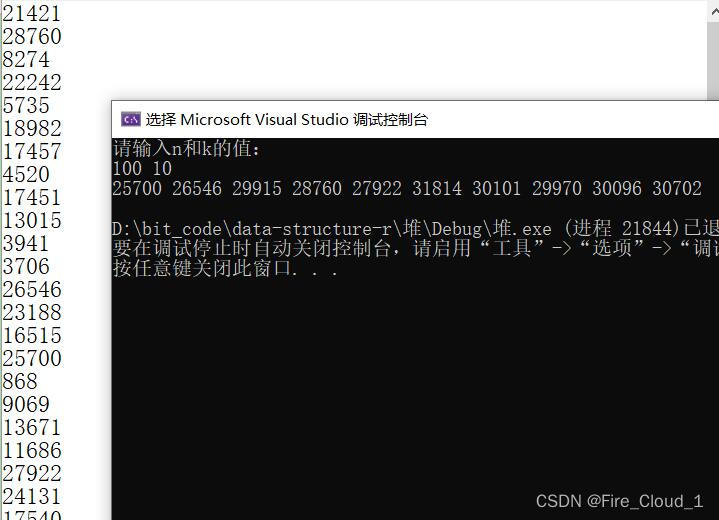
在这里插入图片描述

除了从固定的文件中读取数据进行运算，我们还可以自己写入一些数据进行查找
可以看到，我这里使用的是一个随机值的写入，这一块也是我们在C语言中讲到过的，要使用到rand()和srand()，过程很简单，当然这里的【n】和【k】是由我自己来输入，因此下面的数组我们要设置成动态开辟。代码如下

	int n, k;
	puts("请输入n和k的值：");
	scanf("%d%d", &n, &k);
	srand((unsigned int)time(NULL));		//随机种子

	FILE\* fin = fopen("data2.txt", "w");		//若有，则打开写入；若无，则创建写入
	
	int randVal = 0;
	for (int i = 0; i < n; ++i)
	{
		randVal = rand() % 1000000;		//随机生成数字
		fprintf(fin, "%d\n", randVal);		//将每次随机生成的数字写入文件中
	}
	fclose(fin);

	///
	// 获取文件中前TopK个值
	//1.使用一个文件指针指向这个文件
	FILE\* fout = fopen("data2.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

	//2.读出前k个数放入数组中
	int\* max = (int\*)malloc(sizeof(int) \* k);

	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &max[i]);		//此处无需加\n，因为读取时空格和回车自动作为分隔
	}

	//3.建立k个堆
	for (int i = ((k - 1) - 1) / 2; i >= 0; --i)
	{
		Adjust\_Down(max, k, i);
	}

	//4.继续读取剩下的数据
	/\*
 \* 不断和堆顶数据做比较，比堆顶大就入堆，然后继续向下调整
 \*/
	int val = 0;
	while ((fscanf(fout, "%d", &val)) != EOF)		//不停读取剩下的数据
	{
		if (val > max[0])
		{
			max[0] = val;		//替换为堆顶
			Adjust\_Down(max, k, 0);		//将其做向下调整
		}
	}

	//5.打印数组中的数据，观看TopK个最大的数
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", max[i]);
	}
	printf("\n");
	fclose(fout);

来看看运行结果

在这里插入图片描述

七、整体代码展示【需要自取】

Heap.h

#pragma once

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>
#include <time.h>

typedef int HpDataType;
typedef struct Heap {
	HpDataType\* a;
	int size;
	int capacity;
}Hp;

/\*初始化堆\*/
void HeapInit(Hp\* hp);
/\*建堆\*/
void HeapCreate1(Hp\* hp, HpDataType\* a, int n);		//向上调整
void HeapCreate2(Hp\* hp, HpDataType\* a, int n);		//向下调整
/\*堆的插入\*/
void HeapPush(Hp\* hp, HpDataType x);
/\*堆的删除\*/
void HeapPop(Hp\* hp);
/\*取堆顶数据\*/
HpDataType HeapTop(Hp\* hp);
/\*判断堆是否为空\*/
bool HeapEmpty(Hp\* hp);
/\*返回堆的大小\*/
size_t HeapSize(Hp\* hp);
/\*输出堆\*/
void HeapDisplay(Hp\* hp);
/\*销毁堆\*/
void HeapDestroy(Hp\* hp);

/\*交换函数\*/
void swap(HpDataType\* x1, HpDataType\* x2);
/\*向上调整算法\*/
void Adjust\_UP(Hp\* hp, int child);
/\*向下调整算法\*/
void Adjust\_Down(int\* a, int n, int parent);
/\*堆排序\*/
void HeapSort(int\* a, int n);
/\*TopK\*/
void HeapTopK();
void HeapTopK2();

Heap.cpp

#define \_CRT\_SECURE\_NO\_WARNINGS 1

#include "Heap.h"

/\*初始化堆\*/
void HeapInit(Hp\* hp)
{
	assert(hp);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}

/\*建堆\*/
void HeapCreate1(Hp\* hp, HpDataType\* a, int n)
{
	assert(hp);
	HeapInit(hp);
	for (int i = 0; i < n; ++i)
	{
		HeapPush(hp, a[i]);
	}
}

/\*建堆\*/
void HeapCreate2(Hp\* hp, HpDataType\* a, int n)
{
	assert(hp);
	HeapInit(hp);
	HpDataType\* tmp = (HpDataType\*)malloc(sizeof(HpDataType) \* n);	//首先申请n个空间用来存放原来的堆
	if (tmp == NULL)
	{
		perror("fail malloc");
		exit(-1);
	}
	hp->a = tmp;

	//void \* memcpy ( void \* destination, const void \* source, size\_t num );
	memcpy(hp->a, a, sizeof(HpDataType) \* n);	//将数组a中n个数据拷贝到堆中的数组
	hp->size = n;
	hp->capacity = n;

	//向下调整 
	/\*
 \* （n - 1）代表取到数组最后一个数据，不可以访问n
 \* (x - 1)/2 代表通过孩子找父亲
 \*/
	for (int i = ((n - 1) - 1) / 2; i >= 0; --i)
	{
		Adjust\_Down(hp->a, n, i);
	}
}

/\*交换函数\*/
void swap(HpDataType\* x1, HpDataType\* x2)
{
	HpDataType t = \*x1;
	\*x1 = \*x2;
	\*x2 = t;
}

/\*向上调整算法\*/
/\*
\* 孙子很可能当上爷爷
\*/
void Adjust\_UP(Hp\* hp, int child)
{
	int parent = (child - 1) / 2;

	//while (parent >= 0) 这样写不好，程序会非正常结束
	while (child  > 0)
	{
		if (hp->a[child] > hp->a[parent])
		{
			swap(&hp->a[child], &hp->a[parent]);		//交换孩子和父亲，逐渐变为大根堆
			//迭代 —— 交替更新孩子和父亲
			child = parent;		
			parent = (child - 1) / 2;
		}
		else {
			break;		//若是比较无需交换，则退出循环
		}
	}
}

/\*堆的插入\*/
void HeapPush(Hp\* hp, HpDataType x)
{
	assert(hp);
	//扩容逻辑
	if (hp->size == hp->capacity)
	{
		int newCapacity = hp->capacity == 0 ? 4 : hp->capacity \* 2;
		HpDataType\* tmp = (HpDataType\*)realloc(hp->a, newCapacity \* sizeof(HpDataType));
		if (tmp == NULL)
		{
			perror("fail realloc");
			exit(-1);
		}
		hp->a = tmp;
		hp->capacity = newCapacity;
	}
	hp->a[hp->size] = x;
	hp->size++;

	Adjust\_UP(hp, hp->size - 1);
}

/\*向下调整算法\*/
/\*
\* 高处不胜寒 —— 即使是堆顶，也是不会稳定的，做不住的，会被人打下来，因此需要向下调整
\*/
void Adjust\_Down(int\* a, int n, int parent)
{
	int child = parent \* 2 + 1;		//默认左孩子来得大
	while (child < n)
	{		//判断是否存在右孩子，防止越界访问
		if (child + 1 < n && a[child + 1] < a[child])
		{
			++child;		//若右孩子来的大，则转化为右孩子
		}
		if (a[child] < a[parent])
		{
			swap(&a[child], &a[parent]);
			parent = child;
			child = parent \* 2 + 1;
		}
		else {
			break;
		}
	}
}

/\*堆的删除\*/
void HeapPop(Hp\* hp)
{
	assert(hp);
	assert(hp->size > 0);
	//首先交换堆顶和树的最后一个结点 —— 易于删除数据，保护堆的结构不被破坏
	swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;		//去除最后一个数据

	Adjust\_Down(hp->a, hp->size, 0);
}

/\*取堆顶数据\*/
HpDataType HeapTop(Hp\* hp)
{
	assert(hp);
	assert(hp->size > 0);
	return hp->a[0];
}

/\*判断堆是否为空\*/
bool HeapEmpty(Hp\* hp)
{
	assert(hp);
	return hp->size == 0;
}

/\*返回堆的大小\*/
size_t HeapSize(Hp\* hp)
{
	assert(hp);
	return hp->size;
}

/\*输出堆\*/
void HeapDisplay(Hp\* hp)
{
	for (int i = 0; i < hp->size; ++i)
	{
		printf("%d ", hp->a[i]);
	}
	printf("\n");
}

/\*销毁堆\*/
void HeapDestroy(Hp\* hp)
{
	assert(hp);
	free(hp->a);
	hp->a = NULL;
	hp->size = hp->capacity = 0;
}


/\*堆排序\*/
void HeapSort(int\* a, int n)
{
	//建立大根堆（倒数第一个非叶子结点）
	for (int i = ((n - 1) - 1) / 2 ; i >= 0; --i)
	{
		Adjust\_Down(a, n, i);
	}

	int end = n - 1;
	while (end > 0)
	{
		swap(&a[0], &a[end]);		//首先交换堆顶结点和堆底末梢结点
		Adjust\_Down(a, end, 0);		//一一向前调整
		end--;
	}
}


/\*TopK\*/
void HeapTopK()
{
	//1.使用一个文件指针指向这个文件
	FILE\* fout = fopen("data.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

	//2.读出前k个数放入数组中
	int k = 5;
	int max[5];
	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &max[i]);
	}

	//3.建立k个堆
	for (int i = ((k - 1) - 1) / 2; i >= 0; --i)
	{
		Adjust\_Down(max, k, i);
	}

	//4.继续读取剩下的数据
	/\*
 \* 不断和堆顶数据做比较，比堆顶大就入堆，然后继续向下调整
 \*/
	int val = 0;
	while ((fscanf(fout, "%d", &val)) != EOF)		//不停读取剩下的数据
	{
		if (val > max[0])
		{
			max[0] = val;		//替换为堆顶
			Adjust\_Down(max, k, 0);		//将其做向下调整
		}
	}

	//5.打印数组中的数据，观看TopK个最大的数
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", max[i]);
	}
	printf("\n");
	fclose(fout);
}


void HeapTopK2()
{
	int n, k;
	puts("请输入n和k的值：");
	scanf("%d%d", &n, &k);
	srand((unsigned int)time(NULL));		//随机种子

	FILE\* fin = fopen("data2.txt", "w");		//若有，则打开写入；若无，则创建写入
	
	int randVal = 0;
	for (int i = 0; i < n; ++i)
	{
		randVal = rand() % 1000000;		//随机生成数字
		fprintf(fin, "%d\n", randVal);		//将每次随机生成的数字写入文件中
	}
	fclose(fin);

	///
	// 获取文件中前TopK个值
	//1.使用一个文件指针指向这个文件
	FILE\* fout = fopen("data2.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		return;
	}

	//2.读出前k个数放入数组中
	int\* max = (int\*)malloc(sizeof(int) \* k);

	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &max[i]);		//此处无需加\n，因为读取时空格和回车自动作为分隔
	}

	//3.建立k个堆
	for (int i = ((k - 1) - 1) / 2; i >= 0; --i)
	{
		Adjust\_Down(max, k, i);
	}

	//4.继续读取剩下的数据
	/\*
 \* 不断和堆顶数据做比较，比堆顶大就入堆，然后继续向下调整
 \*/
	int val = 0;
	while ((fscanf(fout, "%d", &val)) != EOF)		//不停读取剩下的数据
	{
		if (val > max[0])
		{
			max[0] = val;		//替换为堆顶
			Adjust\_Down(max, k, 0);		//将其做向下调整
		}
	}

	//5.打印数组中的数据，观看TopK个最大的数
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", max[i]);
	}
	printf("\n");
	fclose(fout);
}

test.cpp

#define \_CRT\_SECURE\_NO\_WARNINGS 1

#include "Heap.h"


![img](/image/aHR0cHM6Ly9pbWctYmxvZy5jc2RuaW1nLmNuL2ltZ19jb252ZXJ0L2E2YzUxZGI1MmNlMzUwMjBkZTY4MjFiZmM3MjY5M2Y5LnBuZw%3D%3D)
![img](https://img-blog.csdnimg.cn/img_convert/d908bfe75513c6ac6879563e1754f9da.png)
![img](https://img-blog.csdnimg.cn/img_convert/6140fd63b4e7c3dc97158f450325e367.png)

**既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上Go语言开发知识点，真正体系化！**

**由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新**

**[如果你需要这些资料，可以戳这里获取](https://bbs.csdn.net/topics/618658159)**

, &max[i]);		//此处无需加\n，因为读取时空格和回车自动作为分隔
	}

	//3.建立k个堆
	for (int i = ((k - 1) - 1) / 2; i >= 0; --i)
	{
		Adjust\_Down(max, k, i);
	}

	//4.继续读取剩下的数据
	/\*
 \* 不断和堆顶数据做比较，比堆顶大就入堆，然后继续向下调整
 \*/
	int val = 0;
	while ((fscanf(fout, "%d", &val)) != EOF)		//不停读取剩下的数据
	{
		if (val > max[0])
		{
			max[0] = val;		//替换为堆顶
			Adjust\_Down(max, k, 0);		//将其做向下调整
		}
	}

	//5.打印数组中的数据，观看TopK个最大的数
	for (int i = 0; i < k; ++i)
	{
		printf("%d ", max[i]);
	}
	printf("\n");
	fclose(fout);
}

test.cpp

#define \_CRT\_SECURE\_NO\_WARNINGS 1

#include "Heap.h"


[外链图片转存中...(img-S3SLRq8Z-1715729145650)]
[外链图片转存中...(img-8WDbyn6q-1715729145650)]
[外链图片转存中...(img-FZkEFIuq-1715729145651)]

**既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上Go语言开发知识点，真正体系化！**

**由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新**

**[如果你需要这些资料，可以戳这里获取](https://bbs.csdn.net/topics/618658159)**

2024年最全数据结构 堆的向上调整和向下调整算法【奇妙的堆排序】(3)，血与泪的总结

改写族谱，关系紊乱😵

5、取堆顶的数据

6、堆的数据个数

7、堆的判空

8、堆的构建

Way1

Way2√

测试💻

五、两种调整算法的复杂度精准剖析⏳

1、向下调整算法【重点掌握】

2、向上调整算法

六、堆的实际应用

1、堆排序【⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐⭐】

升序建大堆 or 小堆❓

如何进一步实现排序❓

2、Top-K问题

复杂度分析

代码详情

七、整体代码展示【需要自取】

悦读

2024年最全数据结构堆的向上调整和向下调整算法【奇妙的堆排序】(3)，血与泪的总结