迭代加深:
迭代加深搜索(Iterative Deepening Search,IDS)是一种结合了深度优先搜索(DFS)和广度优先搜索(BFS)优点的搜索算法,常用于在状态空间较大且目标节点深度未知的情况下寻找最优解。
基本思想
迭代加深搜索本质上是一种有深度限制的深度优先搜索。它通过逐步增加搜索的深度限制,重复进行深度优先搜索,直到找到目标节点为止。每次搜索时,只探索深度不超过当前深度限制的节点。这样既避免了深度优先搜索可能陷入无限深度分支的问题,又不像广度优先搜索那样需要大量的内存来存储所有待扩展的节点。
算法步骤
1初始化深度限制:将初始深度限制 depth_limit 设置为 0。
2进行深度优先搜索:在当前深度限制下,从起始节点开始进行深度优先搜索。搜索过程中,若节点的深度超过当前深度限制,则不再继续扩展该节点。
3检查是否找到目标节点:如果在当前深度限制下找到了目标节点,则搜索结束,返回解;否则,增加深度限制(通常是将 depth_limit 加 1),并重复步骤 2。
适用场景
状态空间较大且目标节点深度未知/比较浅的位置:当搜索空间非常大,无法使用广度优先搜索存储所有待扩展的节点,且不知道目标节点的深度时,迭代加深搜索是一个很好的选择。
需要找到最优解:由于迭代加深搜索是按照深度从小到大的顺序进行搜索的,因此它可以保证找到的解是最优解(即最短路径)。
迭代加深搜索是一种实用的搜索算法,在很多情况下可以平衡时间和空间复杂度,有效地解决搜索问题。
习题1(加成序列):
分析:
这是一道关于序列构造的算法问题,关键在于根据给定的 “加成序列” 条件,构造出以1开始,以指定整数n结束,且长度m最小的序列,同时满足序列递增以及每个元素可由前面元素相加得到的要求。
迭代加深搜索(IDS):由于直接使用 DFS 可能会陷入过深的分支,导致效率低下。迭代加深搜索可以逐步增加搜索深度(即序列长度的上限),每次在限定深度内进行 DFS。当找到满足条件的序列时,即可停止搜索,这样能在一定程度上优化搜索效率,避免不必要的深度搜索
优化策略
剪枝:
单调性剪枝:若通过前面元素相加得到的新数小于或等于序列中最后一个数,不满足递增条件,直接跳过,无需加入序列继续搜索。
最优性剪枝:记录当前找到的最短序列长度,当正在构造的序列长度超过该最短长度时,直接回溯,不再继续构造后续元素。
记忆化:使用一个数据结构(如哈希表)记录已经尝试过的序列状态及其对应的结果。若再次遇到相同状态,直接获取结果,避免重复计算。例如,记录已经构造到特定长度且序列内容相同的情况,后续遇到时不再重复搜索。
伪代码:

双向dfs:
双向深度优先搜索(Bidirectional Depth First Search,简称双向 DFS)是对传统深度优先搜索算法的一种优化改进,通过从起始点和目标点同时进行深度优先搜索,在两者相遇时找到路径,以此来提高搜索效率。
基本原理
传统的深度优先搜索从起始节点出发,沿着一条路径尽可能深地探索,直到找到目标节点或者无法继续探索为止。而双向 DFS 分别从起始节点和目标节点出发,同时进行深度优先搜索。当两个搜索方向的路径在某个节点相遇时,就找到了从起始点到目标点的路径。由于搜索空间是从两端向中间扩展,相比于单向搜索,理论上可以减少搜索的节点数量,从而加快搜索速度。
算法步骤
初始化:分别创建两个搜索队列(或栈,在 DFS 中常用栈实现),一个用于从起始节点开始搜索,另一个用于从目标节点开始搜索;同时创建两个记录节点访问状态的集合,分别记录两个搜索方向已经访问过的节点。
正向搜索:从起始节点开始,按照深度优先搜索的规则,将相邻未访问的节点加入队列,并标记为已访问。
反向搜索:从目标节点开始,同样按照深度优先搜索的规则,将相邻未访问的节点加入队列,并标记为已访问。
检查相遇:每次扩展完一个方向的节点后,检查另一个方向是否已经访问过当前扩展的节点。如果相遇,则说明找到了一条从起始点到目标点的路径,计算路径长度并返回结果。
继续搜索:如果没有相遇,则继续进行正向和反向搜索,直到队列为空(表示没有找到路径)。
适用场景
状态空间较大:当搜索的状态空间非常大时,双向 DFS 可以显著减少搜索的节点数量,提高搜索效率。比如大型地图中的路径搜索、复杂的状态转移问题等。
目标明确:问题中明确知道起始点和目标点,并且从起始点和目标点进行搜索都是可行的情况,适合使用双向 DFS。 但如果目标点不明确或者难以从目标点进行反向搜索,则不适用。
习题2(送礼物):
分析:
在达达送礼物问题中,需要在不超过最大搬运重量 (W) 的限制下,从 (N) 个礼物中选取若干个,使得选取礼物的重量总和最大。
双向 DFS 思路分析
基本思想
双向 DFS 的核心思想是将 (N) 个礼物分成两部分,分别对这两部分进行 DFS 搜索,然后将两部分的结果进行合并,从而减少搜索空间,提高效率。
具体步骤
1,将所有的物品按照从大到小的顺序排序
2,将前k个物品进行搜索,并存储在表中
3,将剩下的nk个物品进行搜索,每一个搜索的结果在表中进行二分查找,找到最大的满足s<=W当前搜索结果 的结果
伪代码:
IDA*算法
IDA(Iterative Deepening A)算法是一种结合了迭代加深搜索(Iterative Deepening Search,IDS)和 A 搜索算法思想的启发式搜索算法。它在状态空间搜索问题中表现出色,常用于解决路径规划、拼图游戏等问题。
基本思想
迭代加深搜索:迭代加深搜索是一种逐步增加搜索深度限制的搜索策略。它从一个较小的深度限制开始,进行深度优先搜索,若未找到目标节点,则增加深度限制,再次进行深度优先搜索,重复这个过程直到找到目标节点。这种策略避免了深度优先搜索可能陷入无限深度分支的问题,同时空间复杂度与深度优先搜索相同,相对较低。
A 算法:A 算法是一种启发式搜索算法,它使用一个启发式函数 (h(n)) 来估计从节点 (n) 到目标节点的代价,结合从起始节点到节点 (n) 的实际代价 (g(n)),得到一个评估函数 (f(n)=g(n)+h(n))。A 算法优先扩展 (f(n)) 值最小的节点,从而引导搜索朝着最有希望的方向进行。 IDA 算法将迭代加深搜索和 A 算法的思想结合起来,在每次迭代加深的深度优先搜索中,使用评估函数 (f(n)) 来判断是否继续扩展节点,若 (f(n)) 超过当前的深度限制,则剪枝。
算法步骤
1. 初始化深度限制:将初始深度限制 (depth_limit) 设置为起始节点的评估函数值 (f(start)=g(start)+h(start)),通常 (g(start) = 0)。
2. 进行深度优先搜索:从起始节点开始进行深度优先搜索,对于每个节点 (n),计算其评估函数值 (f(n)=g(n)+h(n))。 若 (f(n)) 超过当前深度限制 (depth_limit),则剪枝,不再继续扩展该节点。 若 (f(n)) 未超过深度限制,且节点 (n) 为目标节点,则搜索结束,返回路径。 若 (f(n)) 未超过深度限制,且节点 (n) 不是目标节点,则扩展该节点的所有子节点,继续递归搜索。
3. 更新深度限制:若在当前深度限制下未找到目标节点,记录所有被剪枝节点的最小 (f(n)) 值作为新的深度限制 (depth_limit),然后重复步骤 2。
适用场景
状态空间较大:当搜索的状态空间非常大,无法使用广度优先搜索存储所有待扩展的节点时,IDA 算法是一个很好的选择。
需要找到最优解:IDA 算法可以保证找到的解是最优解(即最短路径),适用于对解的质量有较高要求的问题。
启发式信息可用:当问题存在有效的启发式函数时,IDA 算法可以利用启发式信息引导搜索,提高搜索效率。例如在路径规划问题中,可以使用曼哈顿距离、欧几里得距离等作为启发式函数。
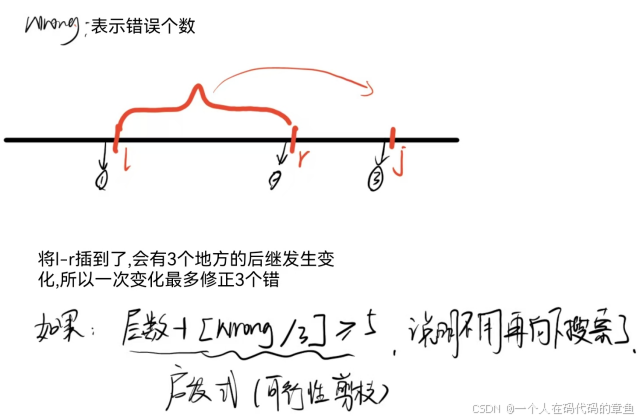
习题3(排书)
分析:
迭代加深搜索(IDA*)思路
状态表示:同 BFS,用列表表示书的排列顺序,同时记录当前操作次数。
初始状态:初始乱序排列的书的列表,操作次数为 0。
状态转移:与 BFS 类似,枚举抽取和插入的情况得到新状态,但在每次转移时增加操作次数。
深度限制与剪枝:设定一个深度限制(即操作次数上限),每次搜索从较小的深度限制开始。若在当前深度限制内搜索到目标状态,则返回结果;若超过深度限制还未找到,则增加深度限制重新搜索。此外,可设计启发式函数,如计算当前排列与目标排列中位置不匹配的书的数量,若当前状态的操作次数加上启发式函数值大于深度限制,则进行剪枝,不再继续搜索该分支。
终止条件:找到目标状态或尝试了足够大的深度限制后仍未找到(可设定一个最大深度限制)。
伪代码:
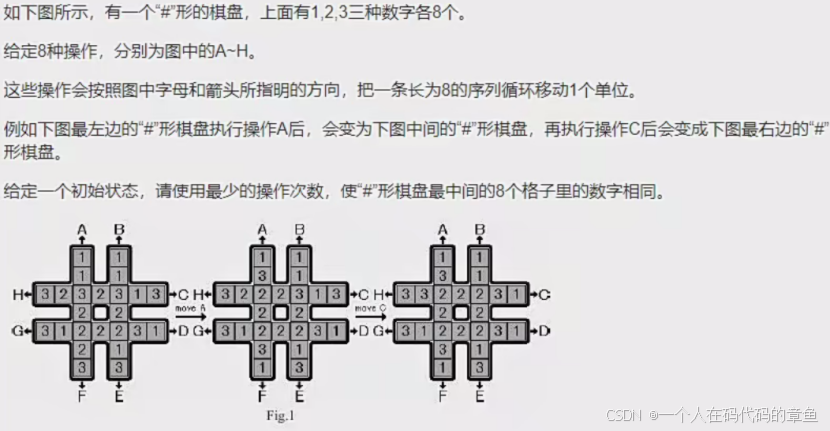
习题4(回转游戏):
分析:
这是一个基于特定操作规则的状态搜索优化问题,目标是通过最少次数的给定操作,使 “#” 形棋盘最中间的 8 个格子数字相同。
迭代加深搜索(IDA*)思路
状态表示:将 “#” 形棋盘的当前数字分布看作一个状态,用一个合适的数据结构(如二维数组或一维数组展开形式)来存储。同时记录达到该状态所使用的操作序列和操作次数。
另外增加一个启发式函数值。
初始状态:初始棋盘状态,操作序列为空,操作次数为 0,启发式函数初始化为根据当前状态计算的值(如中间 8 个格子中不同数字的种类数等,种类数越少说明越接近目标状态)。
状态转移:在当前深度限制下,对当前状态依次应用 8 种操作,生成新状态,并更新操作序列和操作次数,同时重新计算新状态的启发式函数值。
深度限制与剪枝:设定初始深度限制(如 1),每次搜索从这个深度限制开始。若在当前深度限制内找到满足条件的状态,则返回结果;若当前状态的操作次数加上启发式函数值大于深度限制,或者达到了深度限制仍未找到目标状态,则进行剪枝,不再继续搜索该分支。若未找到目标状态,则增加深度限制(如加 1),重新进行搜索。
终止条件:找到目标状态,或者达到一个预先设定的最大深度限制后仍未找到。