一、实验目的
1. 熟练掌插入类排序、交换类排序的实现
2. 掌握选择类排序、非配类的实现
二、实验环境
windows 10、Visual C++6.0
三、实验内容
1. 编写程序,实现直接插入排序算法
#include <stdio.h>
#include <stdlib.h>
typedef int KeyType;
typedef int OtherType;
typedef struct
{
KeyType key;
OtherType other_data;
}RecordType;
void InsSort(RecordType r[], int length)
{
int i,j;
for (i=2; i<=length; i++)
{
r[0]=r[i];
j=i-1;
while (r[0].key< r[j].key )
{
r[j+1]= r[j];
j=j-1;
}
r[j+1]=r[0];
}
} /* InsSort */
void main()
{
int i,j;
RecordType r[20];
int len;
printf("请输入待排序记录的长度:");
scanf("%d",&len);
for(i=1;i<=len;i++)
{
printf("请输入第%d个记录元素:",i);
fflush(stdin);
scanf("%d",&j);
r[i].key = j;
}
for(i=1;i<=len;i++)
printf("%d ",r[i].key);
printf("\n");
InsSort(r,len);
for(i=1;i<=len;i++)
printf("%d ",r[i].key);
printf("\n");
}
//----------------------------------直接插入排序2. 编写程序,实现快速排序算法
#include <stdio.h>
#include <stdlib.h>
typedef int KeyType;
typedef int OtherType;
typedef struct
{
KeyType key;
OtherType other_data;
}RecordType;
int QKPass(RecordType r[],int left,int right)
{
RecordType x;
int low,high;
x= r[left]; /* 选择基准记录*/
low=left;
high=right;
while ( low<high )
{
while (low< high && r[high].key>=x.key )
/* high从右到左找小于x.key的记录 */
high--;
if ( low <high )
{
r[low]= r[high];
low++;
}
/* 找到小于x.key的记录,则进行交换*/
while (low<high && r[low].key<x.key )
low++;
if ( low<high )
{
r[high]= r[low];
high--;
} /* 找到大于x.key的记录,则交换*/
}
r[low]=x; /*将基准记录保存到low=high的位置*/
return low; /*返回基准记录的位置*/
} /* QKPass */
void QKSort(RecordType r[],int low, int high )
/*对记录数组r[low..high]用快速排序算法进行排序*/
{
int pos;
if(low<high)
{
pos=QKPass(r, low, high); /*调用一趟快速排序,将枢轴元素为界划分两个子表*/
QKSort(r, low, pos-1); /*对左部子表快速排序*/
QKSort(r, pos+1, high); /*对右部子表快速排序*/
}
}
void main()
{
int i,j;
RecordType r[20];
int len;
printf("请输入待排序记录的长度:");
scanf("%d",&len);
for(i=1;i<=len;i++)
{
printf("请输入第%d个记录元素:",i);
fflush(stdin);
scanf("%d",&j);
r[i].key = j;
}
for(i=1;i<=len;i++)
printf("%d ",r[i].key);
printf("\n");
QKSort(r,1,len);
for(i=1;i<=len;i++)
printf("%d ",r[i].key);
printf("\n");
}
//----------------------------------快速排序3. 编写程序,实现归并排序算法
#include <stdio.h>
#include <stdlib.h>
typedef int KeyType;
typedef int OtherType;
typedef struct
{
KeyType key;
OtherType other_data;
}RecordType;
void Merge(RecordType r1[], int low, int mid, int high, RecordType r2[])
/* 已知r1[low..mid]和r1[mid+1..high]分别按关键字有序排列,将它们合并成一个有序序列,存放在r2[low..high] */
{
int i,j,k;
i=low;
j=mid+1;
k=low;
while ( (i<=mid)&&(j<=high) )
{
if ( r1[i].key<=r1[j].key )
{
r2[k]=r1[i];
++i;
}
else
{
r2[k]=r1[j];
++j;
}
++k;
}
while( i<=mid )
{
r2[k]=r1[i];
k++;
i++;
}
while( j<=high)
{
r2[k]=r1[j];
k++;
j++;
}
} /* Merge */
void MSort(RecordType r1[], int low, int high, RecordType r3[])
/* r1[low..high]经过排序后放在r3[low..high]中,r2[low..high]为辅助空间 */
{
int mid;
RecordType r2[20];
if ( low==high )
r3[low]=r1[low];
else
{
mid=(low+high)/2;
MSort(r1,low, mid, r2);
MSort(r1,mid+1,high, r2);
Merge (r2,low,mid,high, r3);
}
} /* MSort */
void MergeSort ( RecordType r[], int n )
/* 对记录数组r[1..n]做归并排序 */
{
MSort ( r, 1, n, r );
}
void main()
{
int i,j;
RecordType r[20];
int len;
printf("请输入待排序记录的长度:");
scanf("%d",&len);
for(i=1;i<=len;i++)
{
printf("请输入第%d个记录元素:",i);
fflush(stdin);
scanf("%d",&j);
r[i].key = j;
}
for(i=1;i<=len;i++)
printf("%d ",r[i].key);
printf("\n");
MergeSort(r,len);
for(i=1;i<=len;i++)
printf("%d ",r[i].key);
printf("\n");
}
//----------------------------------归并排序四、实验结果与分析
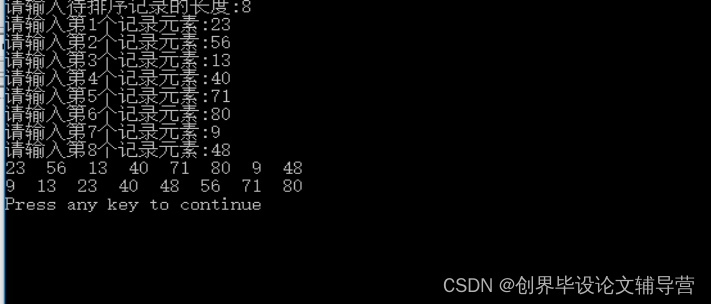
图1 第1题运行结果图
分析:直接插入排序(Straight Insertion Sort)的基本操作是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增1的有序表,同样的O(n^2)时间复杂度,直接插入排序比选择排序和冒泡排序性能要要一些。直接插入排序对数组基本有序和数组元素比较少的时候,速度比较快。
2.
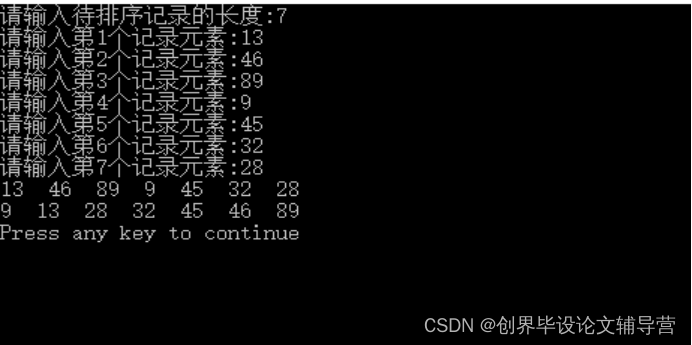
图2 第2题运行结果图
分析:快速排序算法的时间复杂度和各次标准数据元素的值关系很大。如果每次选取的标准元素都能均分两个子数组的长度,这样的快速排序过程是一个完全二叉树结构。(即每个结点都把当前数组分成两个大小相等的数组结点,n个元素数组的根结点的分解次数就构成一棵完全二叉树)。这时分解次数等于完全二叉树的深度log2n;每次快速排序过程无论把数组怎样划分、全部的比较次数都接近于n-1次,所以最好情况下快速排序算法的时间复杂度为O(nlog2n)。
3.
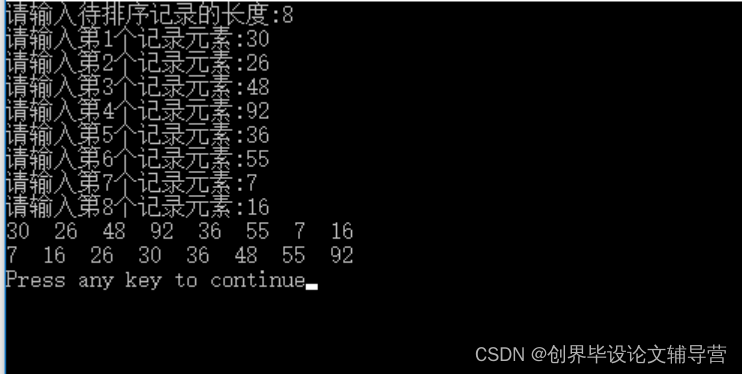
图3 第3题运行结果图
分析:归并排序的过程中,需要对当前区间进行对半划分,直到区间的长度为1。也就是说,每一层的子区间,长度都是上一层的1/2。这也就意味着,当划分到第logn层的时候,子区间的长度就是1了。而归并排序的merge操作,则是从最底层开始(子区间为1的层),对相邻的两个子区间进行合并,过程如下:在logn层(最底层),每个子区间的长度为1,共n个子区间,每相邻两个子区间进行合并,总共合并n/2次。n个数字都会被遍历一次,所有这一层的总时间复杂度为o(n).