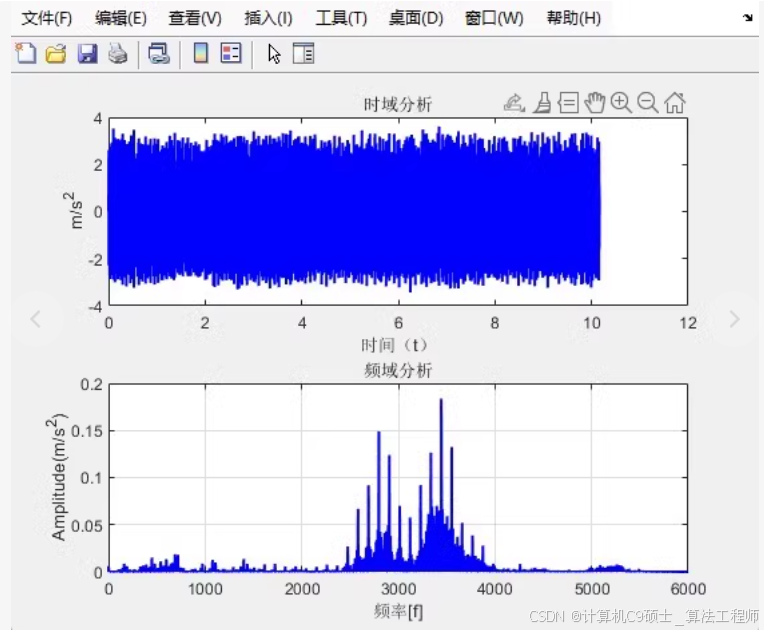
如何利用凯斯西储大学轴承数据图 更换数据集,
包括原始信号图,➕时域频域对比图,➕模态分解图+包络谱图,怎么做?
使用凯斯西储大学轴承数据集来构建一个完整的分析流程,包括原始信号图、时域频域对比图、模态分解图和包络谱图。以下是详细的步骤和代码示例。
文章代码仅供参考
数据集说明
凯斯西储大学轴承数据集包含了各种故障状态下的振动信号数据。这些数据通常是以 .mat 文件的形式提供的。所有需要读取这些文件并进行相应的处理和可视化。
环境部署说明
首先,确保你已经安装了必要的库。以下是详细的环境部署步骤:
安装依赖
# 创建虚拟环境(可选)
conda create -n bearing_analysis_env python=3.9
conda activate bearing_analysis_env
# 安装PyTorch和其他依赖
pip install torch==1.9 torchvision torchaudio --extra-index-url https://download.pytorch.org/whl/cu111
pip install numpy scipy matplotlib pywt scikit-learn pandas seaborn
数据加载和预处理
我们将编写代码来加载 .mat 文件中的数据,并进行一些基本的预处理。
数据加载脚本 load_data.py
[<title="Loading and Preprocessing CWRU Bearing Data">]
import os
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
# Define paths
data_path = 'path/to/CWRU/bearing/data'
# Load .mat file
file_name = '97.mat' # Example file name
file_path = os.path.join(data_path, file_name)
data = sio.loadmat(file_path)
# Extract data
signal = data['X097_DE_time'].flatten() # Assuming 'X097_DE_time' is the key for the signal
# Plot original signal
plt.figure(figsize=(15, 5))
plt.plot(signal)
plt.title('Original Signal')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')
plt.show()
请将 path/to/CWRU/bearing/data 替换为实际的数据集路径,并根据实际情况调整文件名和键值。
时域频域对比图
我们将编写代码来生成时域和频域的对比图。
时域频域对比图脚本 time_frequency_plot.py
[<title="Time-Frequency Domain Comparison for CWRU Bearing Data">]
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
# Assume signal is already loaded from load_data.py
# signal = ...
# Compute FFT
N = len(signal)
yf = fft(signal)
xf = fftfreq(N, 1 / 12000) # Sampling frequency of 12 kHz
# Take only positive frequencies
xf = xf[:N // 2]
yf = yf[:N // 2]
# Plot time-domain and frequency-domain signals
plt.figure(figsize=(15, 10))
plt.subplot(2, 1, 1)
plt.plot(signal)
plt.title('Time-Domain Signal')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')
plt.subplot(2, 1, 2)
plt.plot(xf, np.abs(yf))
plt.title('Frequency-Domain Signal')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.xlim([0, 1000]) # Limit x-axis to 1000 Hz for better visualization
plt.tight_layout()
plt.show()
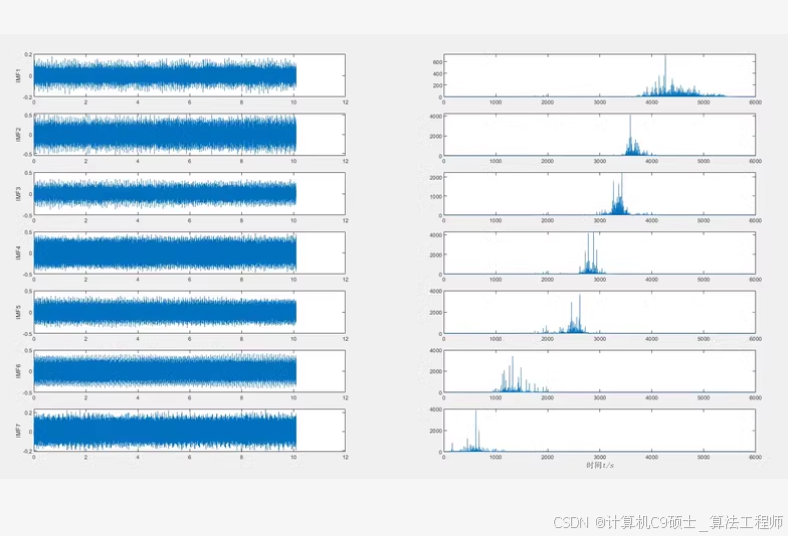
模态分解图
我们将使用经验模态分解(EMD)来进行模态分解,并绘制结果。
模态分解图脚本 emd_plot.py
[<title="Empirical Mode Decomposition for CWRU Bearing Data">]
import numpy as np
import matplotlib.pyplot as plt
from PyEMD import EMD
# Assume signal is already loaded from load_data.py
# signal = ...
# Perform EMD
emd = EMD()
IMFs = emd.emd(signal)
# Plot IMFs
plt.figure(figsize=(15, 10))
for i, imf in enumerate(IMFs):
plt.subplot(len(IMFs), 1, i + 1)
plt.plot(imf)
plt.title(f'IMF {i + 1}')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')
plt.tight_layout()
plt.show()
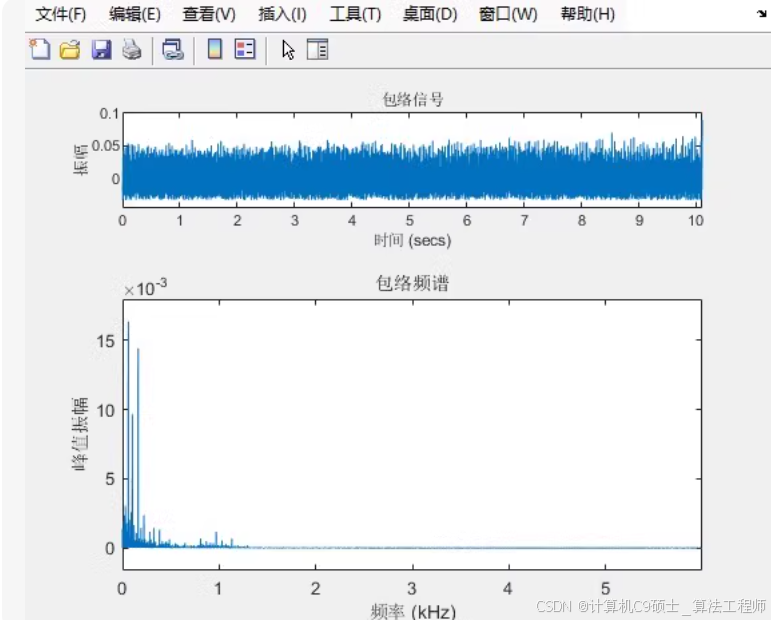
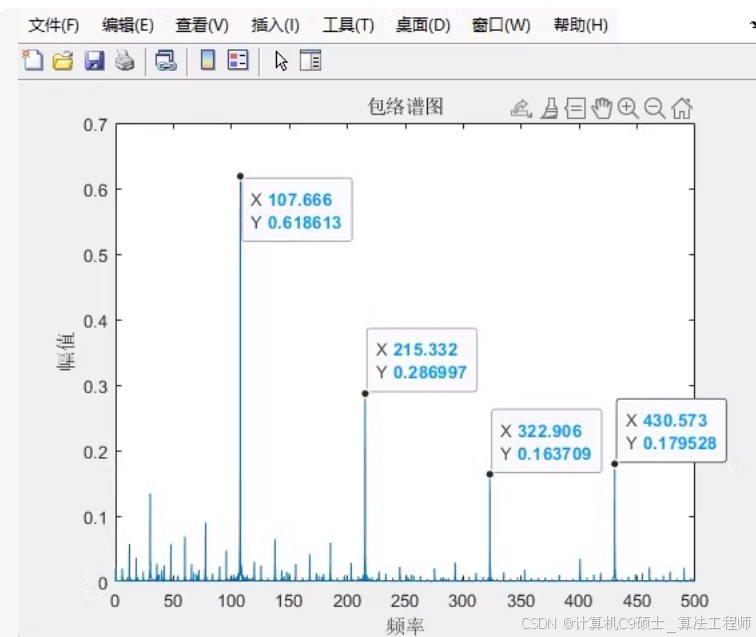
包络谱图
我们将计算包络谱图来提取特征。
包络谱图脚本 envelope_spectrum_plot.py
[<title="Envelope Spectrum for CWRU Bearing Data">]
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import hilbert
from scipy.fft import fft, fftfreq
# Assume signal is already loaded from load_data.py
# signal = ...
# Hilbert Transform
analytic_signal = hilbert(signal)
amplitude_envelope = np.abs(analytic_signal)
# Compute FFT of envelope
N = len(amplitude_envelope)
yf = fft(amplitude_envelope)
xf = fftfreq(N, 1 / 12000) # Sampling frequency of 12 kHz
# Take only positive frequencies
xf = xf[:N // 2]
yf = yf[:N // 2]
# Plot Envelope Spectrum
plt.figure(figsize=(15, 5))
plt.plot(xf, np.abs(yf))
plt.title('Envelope Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.xlim([0, 1000]) # Limit x-axis to 1000 Hz for better visualization
plt.tight_layout()
plt.show()
整合所有图表
我们可以将上述所有图表整合到一个脚本中,以便一次性生成所有的可视化结果。
综合可视化脚本 full_visualization.py
[<title="Full Visualization for CWRU Bearing Data">]
import os
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from scipy.fft import fft, fftfreq
from PyEMD import EMD
from scipy.signal import hilbert
# Define paths
data_path = 'path/to/CWRU/bearing/data'
# Load .mat file
file_name = '97.mat' # Example file name
file_path = os.path.join(data_path, file_name)
data = sio.loadmat(file_path)
# Extract data
signal = data['X097_DE_time'].flatten() # Assuming 'X097_DE_time' is the key for the signal
# Compute FFT
N = len(signal)
yf = fft(signal)
xf = fftfreq(N, 1 / 12000) # Sampling frequency of 12 kHz
# Take only positive frequencies
xf = xf[:N // 2]
yf = yf[:N // 2]
# Perform EMD
emd = EMD()
IMFs = emd.emd(signal)
# Hilbert Transform
analytic_signal = hilbert(signal)
amplitude_envelope = np.abs(analytic_signal)
# Compute FFT of envelope
yf_env = fft(amplitude_envelope)
xf_env = fftfreq(N, 1 / 12000) # Sampling frequency of 12 kHz
# Take only positive frequencies
xf_env = xf_env[:N // 2]
yf_env = yf_env[:N // 2]
# Plot all figures
plt.figure(figsize=(15, 20))
# Original Signal
plt.subplot(4, 1, 1)
plt.plot(signal)
plt.title('Original Signal')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')
# Time-Domain and Frequency-Domain Signals
plt.subplot(4, 1, 2)
plt.plot(xf, np.abs(yf))
plt.title('Frequency-Domain Signal')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.xlim([0, 1000])
# Empirical Mode Decomposition
plt.subplot(4, 1, 3)
for i, imf in enumerate(IMFs):
plt.plot(imf, label=f'IMF {i + 1}', alpha=0.7)
plt.title('Empirical Mode Decomposition')
plt.xlabel('Sample Index')
plt.ylabel('Amplitude')
plt.legend()
# Envelope Spectrum
plt.subplot(4, 1, 4)
plt.plot(xf_env, np.abs(yf_env))
plt.title('Envelope Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.xlim([0, 1000])
plt.tight_layout()
plt.show()
总结
通过以上步骤,完成从数据加载、预处理到生成各种可视化图表的过程。以下是所有相关的代码文件:
- 数据加载脚本 (
load_data.py) - 时域频域对比图脚本 (
time_frequency_plot.py) - 模态分解图脚本 (
emd_plot.py) - 包络谱图脚本 (
envelope_spectrum_plot.py) - 综合可视化脚本 (
full_visualization.py)
。