牛客练习赛134 B

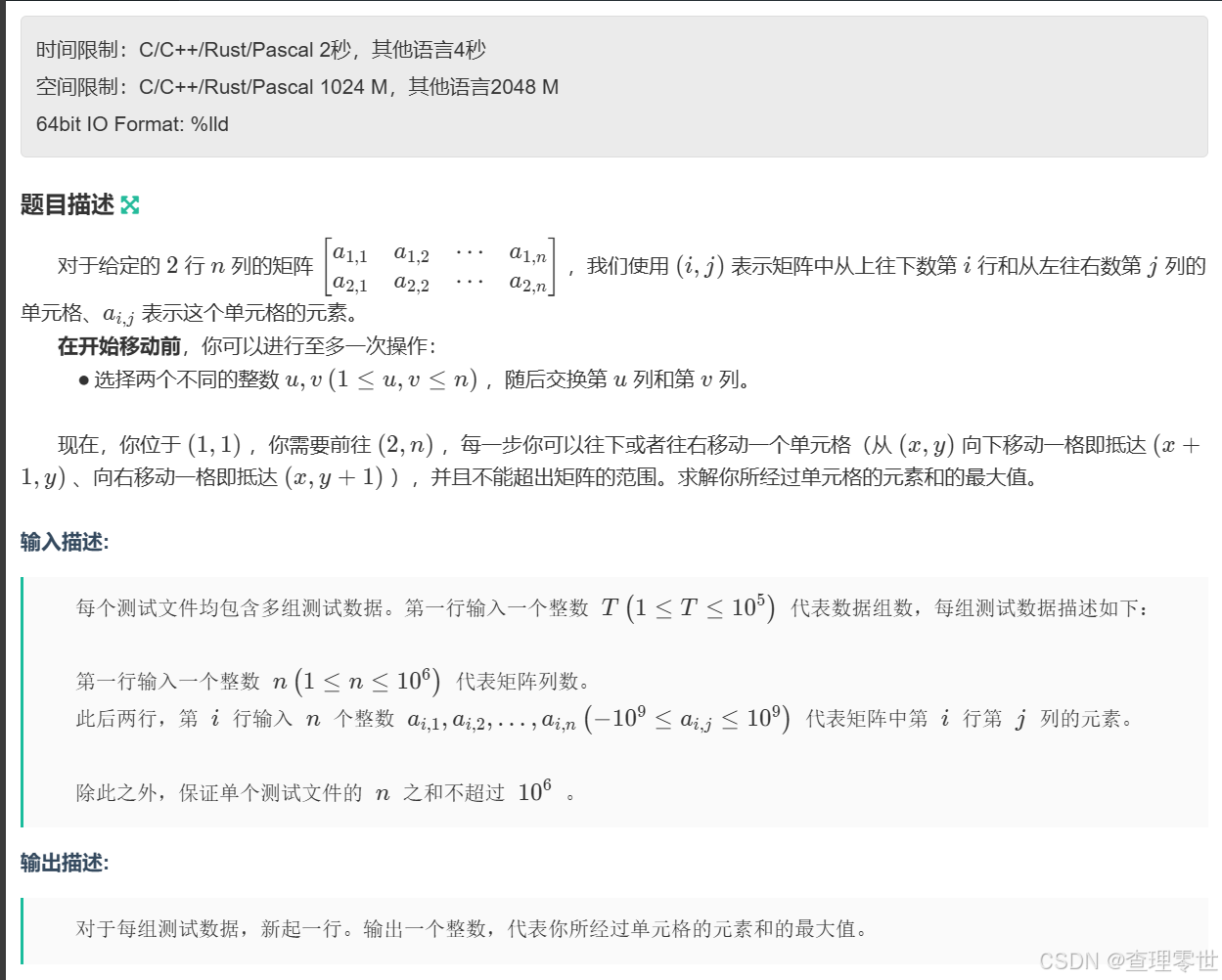
题目描述

示例输入：

1
5
1 2 4 5 6
2 5 4 6 9

示例输出：

32

解题思路：

题目大意

给定一个2行n列的矩阵，允许交换两列一次，从左上角(1,1)走到右下角(2,n)，每一步只能向右或向下移动，求经过元素的最大和。

核心思路: 往下走只有一次，所以选择枚举往下走的分界点

1. 路径结构分析
   路径必然在第一行右走若干列后下到第二行继续右走。设转折点为i（在第i列下移），路径和为第一行前i列的和 + 第二行i到n列的和。

2. 不交换列的情况
   预处理第一行的前缀和sum1和第二行的后缀和sum2，遍历所有i，计算sum1[i]+sum2[i]的最大值。

3. 交换列的增益计算
   通过预处理四个数组，分三种情况计算交换后的最大增益：

   • Case1：交换左半区某列与右半区某列，最大化差值之和。
   • Case2：交换左半区某列与当前列，提升当前列的第二行值。
   • Case3：交换右半区某列与当前列，提升当前列的第一行值。

4. 边界处理
   单独处理i=1和i=n的情况，分别考虑与右侧或左侧列交换的增益。

实现步骤

1. 预处理前缀和与后缀和

   • sum1[i]：第一行前i列的和。
   • sum2[i]：第二行i到n列的和。

2. 预处理最大值与差值数组

   • max1[i]：i到n列第一行的最大值。
   • max2[i]：前i列第二行的最大值。
   • diff1[i]：i到n列（第一行-第二行）的最大差值。
   • diff2[i]：前i列（第二行-第一行）的最大差值。

3. 分情况计算最大路径和

   • 遍历中间转折点，计算三种交换情况的增益。
   • 单独处理首尾列的交换增益。

实现code：

t = int(input())
for _ in range(t):
    n = int(input())
    a1 = list(map(int, input().split()))
    a2 = list(map(int, input().split()))
    ans = -float('inf')

    if n == 1:  # 特判
        print(a1[0] + a2[0])
        continue

    # 第一行的前缀和：sum1[i]表示前i列第一行的元素和
    sum1 = [0] * (n + 1)
    for i in range(1, n + 1):
        sum1[i] = sum1[i - 1] + a1[i - 1]

    # 第二行的后缀和：sum2[i]表示从第i列到第n列第二行的元素和
    sum2 = [0] * (n + 2)
    for i in range(n, 0, -1):
        sum2[i] = sum2[i + 1] + a2[i - 1]

    # 枚举所有可能的分界点i，路径为:前i列走第一行，第i列到第n列走第二行
    for i in range(1, n + 1):
        ans = max(ans, sum1[i] + sum2[i])  # 不交换列的情况

    '''
    预处理max1,max2和diff1,diff2数组：
    max1[i]:第i列到第n列第一行的最大值
    max2[i]:前i列中第二行的最大值
    diff1[i]:第i列到第n列中（第一行元素 - 第二行元素）的最大差值
    diff2[i]:前i列中（第二行元素 - 第一行元素）的最大差值
    '''
    max1 = [-float('inf')] * (n + 2)
    diff1 = [-float('inf')] * (n + 2)
    for i in range(n, 0, -1):
        max1[i] = max(max1[i + 1], a1[i - 1])
        diff1[i] = max(diff1[i + 1], a1[i - 1] - a2[i - 1])

    max2 = [-float('inf')] * (n + 1)
    diff2 = [-float('inf')] * (n + 1)
    for i in range(1, n + 1):
        max2[i] = max(max2[i - 1], a2[i - 1])
        diff2[i] = max(diff2[i - 1], a2[i - 1] - a1[i - 1])

    # 交换列
    for i in range(2, n):
        # Case1：交换i左边某列和右边某列:找到最大的左边差值与右边差值之和
        case1 = sum1[i] + sum2[i] + diff2[i - 1] + diff1[i + 1]
        # Case2：交换i左边某列与当前列:当前列的第二行被替换为左边更大的值
        case2 = sum1[i] + sum2[i] - a2[i - 1] + max2[i - 1]
        # Case3：交换i右边某列与当前列:当前列的第一行被替换为右边更大的值
        case3 = sum1[i] + sum2[i] - a1[i - 1] + max1[i + 1]
        ans = max(ans, case1, case2, case3)

    # 特判：转折点为第一列,最后一列
    if n >= 2:
        # Case4：交换第一列与右边某列：第一列的第一行被替换为右边更大的值
        case4 = sum1[1] + sum2[1] - a1[0] + max1[2]
        # Case5：交换最后一列与左边某列：最后一列的第二行被替换为左边更大的值
        case5 = sum1[n] + sum2[n] - a2[n - 1] + max2[n - 1]
        ans = max(ans, case4, case5)

    print(ans)

END
如果有更多问题或需要进一步的帮助，可以在评论区留言讨论哦！
如果喜欢的话，请给博主点个关注 谢谢