Hello,大家好!很高兴我们又见面了!
给生活添点passion,开始今天的编程之路!
今天我们来从0开始,设计一个较完美的质数计算程序。
目录
1、质数计算程序第一版
要求,计算1到1000的所有质数并输出到屏幕上。
首先我们来明确,什么是质数呢?
定义:一个自然数,只有1和它本身两个因数,这样的数叫做质数(或素数)。
那么我们很容易就想到用穷举法,把这个数除以小于这个数的所有数,如果能整除,他就不是质数,所有都不能整除,他就是质数呗?
我们先把这串代码写出来
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
for (i = 2;i <= 1000;i++)//1不是质数,所以从2开始算
{
for (j = 2;j < i;j++)
{
if (i % j == 0)//如果能整除,跳出循环
{
break;
}
}
if (j == i)
{
printf("%4d", i);
}
}
return 0;
}题目是解决了,可是这样我们要判断1000次!未免也太多了吧?我们定义变量count,检测这个程序计算了多少次运算
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
int count=0;
for (i = 2;i <= 1000;i++)
{
for (j = 2;j < i;j++)
{
count++;
if (i % j == 0)
{
break;
}
}
if (j == i)
{
printf("%4d", i);
}
}
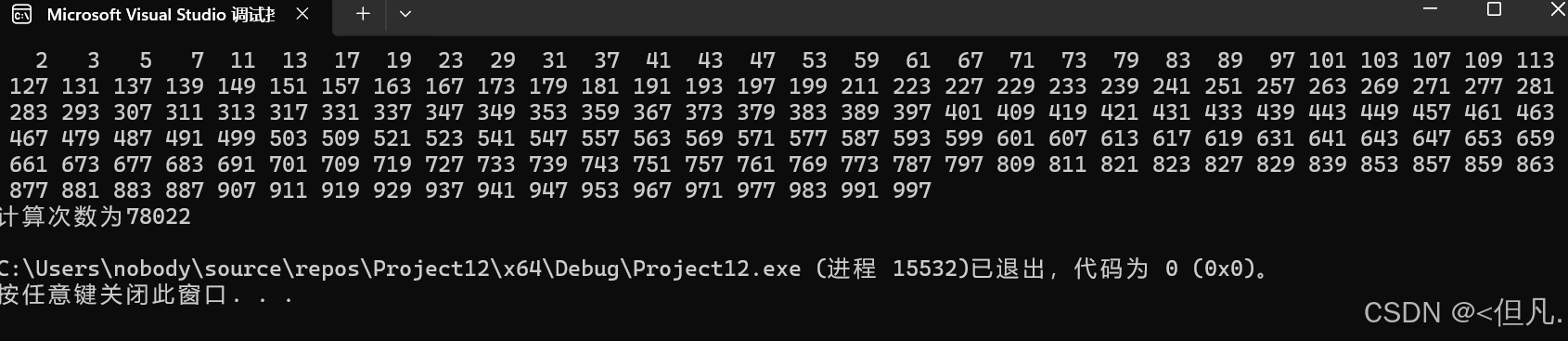
printf("\n计算次数为%d\n", count);
return 0;
}可以发现,计算量是非常大的,这无疑会浪费很多时间。所以接下来我们要进一步优化这个程序。
2、质数计算程序第二版
我们发现:所有质数都是单数。
为什么呢?如果一个数是双数,那他肯定你呢个整除2啊!所以我们这里取消对所有双数的判断,以减少判断次数。
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
int count=0;
printf("%d", 2);//2是一个特例,所以我们先把他打印出来。
for (i = 3;i <= 1000;i+=2)
{
for (j = 3;j < i;j++)
{
count++;
if (i % j == 0)
{
break;
}
}
if (j == i)
{
printf("%4d", i);
}
}
printf("\n计算次数为%d\n", count);
return 0;
}
3、质数计算程序第三版
我们发现,质数都无法被双数(2、4、6…)整除。
倘若一个数是质数,那他必然不能被双数整除。倘若一个数不是质数,由于第二版的设计,我们只判断单数,单数是不能被双数整除的(双数乘任意数必然是双数,不可能是单数),既然这些数都不能被双数整除,所以我们可以把被除数的双数都去掉。
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
int count=0;
printf("%d", 2);//2是一个特例,所以我们先把他打印出来。
for (i = 3;i <= 1000;i+=2)
{
for (j = 3;j < i;j+=2)
{
count++;
if (i % j == 0)
{
break;
}
}
if (j == i)
{
printf("%4d", i);
}
}
printf("\n计算次数为%d\n", count);
return 0;
}
4、质数计算程序第四版
我们发现,如果一个数不能整除3,那他也不能整除3的倍数。
如果一个数不能整除5,那他也不能整除5的倍数。
实际上,三的倍数也是由几个三构成的,倘若你不能整除3,又怎么能整除5呢?
比方说现在我们判断11是不是质数,我们只用整除3 5 7 ,不用整除9,因为9是3的倍数。既然9是三的倍数,那么他可以整除3,也就是说9不是质数。我们可以再举例,判断17是不是质数,我们只需要整除3 5 7 11 13 ,不用判断15和9,因为15和9分别是5和3的倍数。而15也不是质数。所以说现在我们可以得到一个结论:
质数无法被小于自己的质数整除。
现在我们对程序进行优化:
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
int count=0;
int arr[500] = { 0 };
int ptr = 0;
arr[ptr++] = 2;
arr[ptr++] = 3;//将第一位被除质数放入数组中
for (i = 5;i <= 1000;i+=2)
{
for (j = 1;j < ptr;j++)//从1开始,去除了2这个双数特例
{
count++;
if (i % arr[j] == 0)
{
break;
}
}
if (j == ptr)
{
arr[ptr++] = i;//将质数存到数组中
}
}
for (i = 0;i < ptr;i++)//循环打印数组
{
printf("%4d", arr[i]);
}
printf("\n计算次数为%d\n", count);
return 0;
}
5、质数计算程序第五版
现在我们来进行最关键的一步。
我们发现,如果检测15是不是质数,由于3乘5等于15,那么我们检测完三就不需要检测十五了。
所以,我们只需要整除 被检测数的开方 之前的质数就可以了。
现在我们实现该代码
#include<stdio.h>
int main()
{
int i = 0;
int j = 0;
int count=0;
int arr[500] = { 0 };
int ptr = 0;
arr[ptr++] = 2;
arr[ptr++] = 3;//将第一位被除质数放入数组中
for (i = 5;i <= 1000;i+=2)
{
int flag = 1;//标记
for (j = 1;arr[j]*arr[j]<=i;j++)//从1开始,去除了2这个双数特例
{
count++;
if (i % arr[j] == 0)
{
flag = 0;
break;
}
}
if (flag)
{
arr[ptr++] = i;//将质数存到数组中
}
}
for (i = 0;i < ptr;i++)//循环打印数组
{
printf("%4d", arr[i]);
}
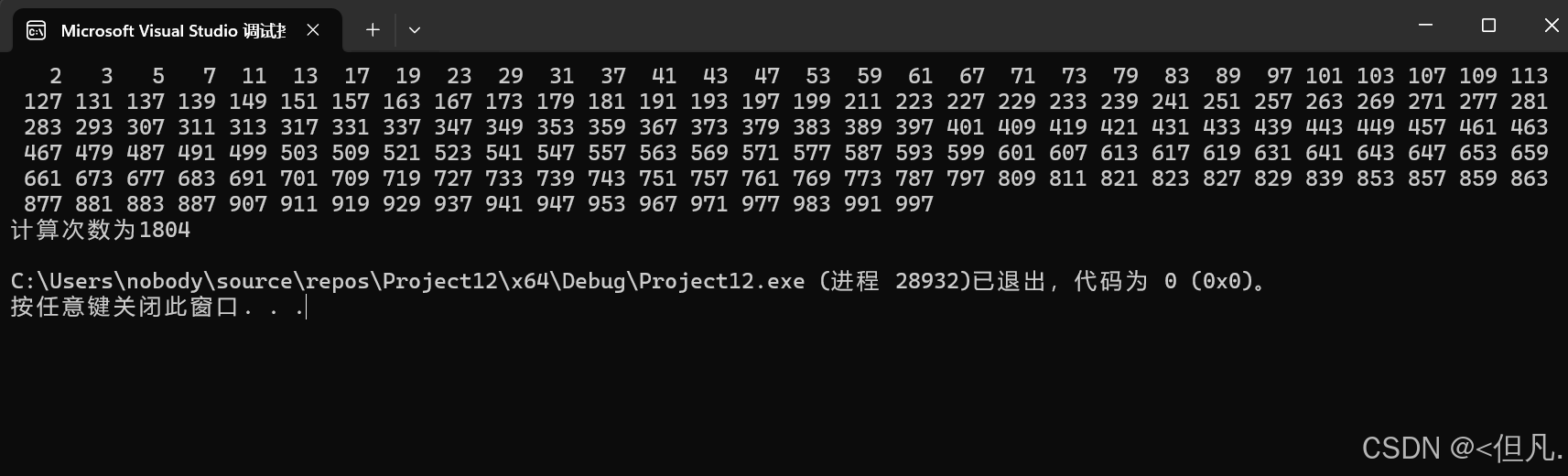
printf("\n计算次数为%d\n", count);
return 0;
}因为我们的被检测数小于1000,所以不会产生溢出的情况。如果被检测数非常的的话,需要写成这种方式来预防溢出
#include<stdio.h>
#include<math.h>
int main()
{
int i = 0;
int j = 0;
int count=0;
int arr[500] = { 0 };
int ptr = 0;
arr[ptr++] = 2;
arr[ptr++] = 3;//将第一位被除质数放入数组中
for (i = 5;i <= 1000;i+=2)
{
int flag = 1;//标记
for (j = 1;arr[j]<=floor(sqrt(i)+0.5);j++)//从1开始,去除了2这个双数特例
{
count++;
if (i % arr[j] == 0)
{
flag = 0;
break;
}
}
if (flag)
{
arr[ptr++] = i;//将质数存到数组中
}
}
for (i = 0;i < ptr;i++)//循环打印数组
{
printf("%4d", arr[i]);
}
printf("\n计算次数为%d\n", count);
return 0;
}由于sqrt开方之后会向下舍入,造成误差,所以我们先给他加上0.5,再floor向下舍入,相当于四舍五入了。这样做可以防止数据溢出(但我们这个程序其实没有这个顾虑),并且尽可能增加准确度,但是会极少量增加计算量,建议根据情况使用。
好了,到目前为止我们的质数计算程序就设计完了,现在我们应用一下。
6、孪生素数
如果n和n+2都是素数(质数),则称他们为孪生素数。输入m,输出两个数均不超过m的最大孪生素数。
我们先将质数判断程序封装成函数
#include<stdio.h>
#include<math.h>
int test(int arr[500],int i)
{
int j = 0;
if (i == 0)
{
return 0;
}
for (j = 1;arr[j] <= floor(sqrt(i) + 0.5);j++)//从1开始,去除了2这个双数特例
{
if (i % arr[j] == 0)
{
return 0;
}
}
return 1;
}
int main()
{
int i = 0;
int a = 0;
int count=0;
int arr[500] = { 0 };
int ptr = 0;
arr[ptr++] = 2;
arr[ptr++] = 3;//将第一位被除质数放入数组中
for (i = 5;i <= 1000;i+=2)
{
a=test(arr,i);
if (a == 1)
{
arr[ptr++] = i;
}
}
for (i = 0;i < ptr;i++)//循环打印数组
{
printf("%4d", arr[i]);
}
return 0;
}现在我们稍作改造,实现代码:
#include<stdio.h>
#include<math.h>
int test(int arr[500],int i)
{
int j = 0;
if (i == 0)
{
return 0;
}
for (j =1;arr[j] <= floor(sqrt(i) + 0.5);j++)//从1开始,去除了2这个双数特例
{
if (i % arr[j] == 0)
{
return 0;
}
}
if (i % 2 == 1)//如果是双数,返回0
{
return 1;
}
else
return 0;
}
int main()
{
int i = 0;
int a = 0;
int m=0;
int arr[500] = { 0 };
int ptr = 0;
printf("请输入数字:");
scanf_s("%d", &m);
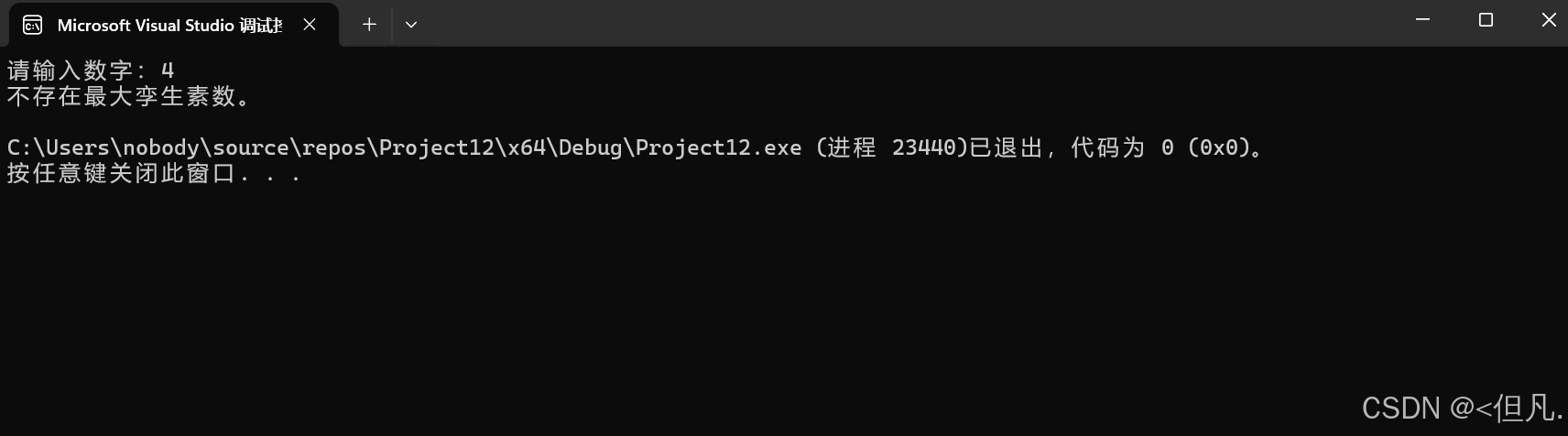
if (m < 5)
{
printf("不存在最大孪生素数。\n");
}
arr[ptr++] = 2;
arr[ptr++] = 3;//将第一位被除质数放入数组中
for (i = 5;i<=m;i+=2)
{
a=test(arr,i);
if (a == 1)
{
arr[ptr++] = i;
}
}
for (i = m - 2;i > 2;i--)
{
if (test(arr, i) == 1 && test(arr, i + 2) == 1)
{
printf("%d %d", i, i + 2);
break;
}
}
return 0;
}运行结果示例:
好了,今天的内容就分享到这,期待我们的下次见面!