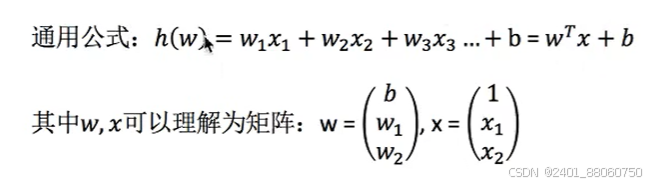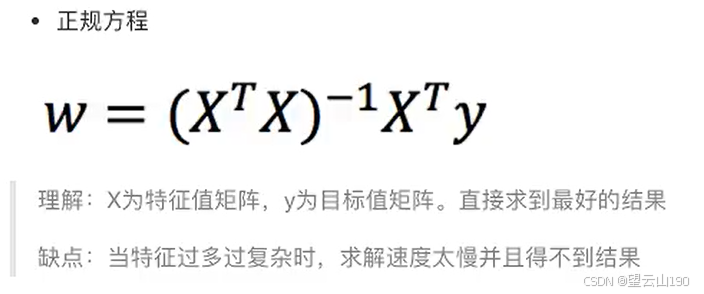4.1.1 线性回归的原理

1 线性回归应用场景：

房价预测

销售额度预测

金融：贷款额度预测，利用线性回归以及系数分析因子

2 什么是线性回归

1） 定义：利用回归方程（函数）对一个或者多个自变量（特征值）和因变量（目标值）之间关系进行建模的一种分析方式。

2）特点：只有一个自变量的情况称为单变量回归，多于一个自变量情况叫做多元回归。

线性关系不等同于线性模型。

线性模型有两种：自变量一次，参数一次

而线性关系就是自变量与参数都是一次的。

4.1.2 线性回归的损失和优化原理

目标：求模型参数

           模型参数能够使得预测准确

损失函数/cost/成本函数/目标函数/最小二乘法：含义相同，只是名字不同

1 损失函数

2 优化算法

1)正规方程

如何去求模型当中的w，使得损失最小？（目的是找到最小损失对应的w的值）

线性回归经常使用的两种优化算法有：正规方程（天才，直接求解w），梯度下降（普通人，试错，改进）

拓展：y=ax^2+bx+c

           y'=2ax+b=0

           x=-b/2a 

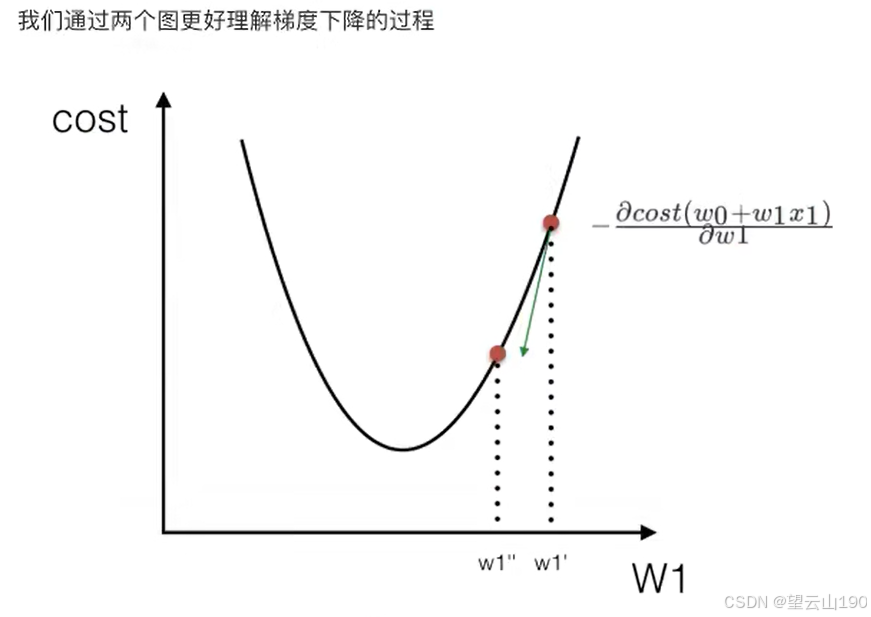
2）梯度下降

所以有了“梯度下降”这一优化算法，回归就有了“自动学习”的能力。

4.1.3 线性回归API

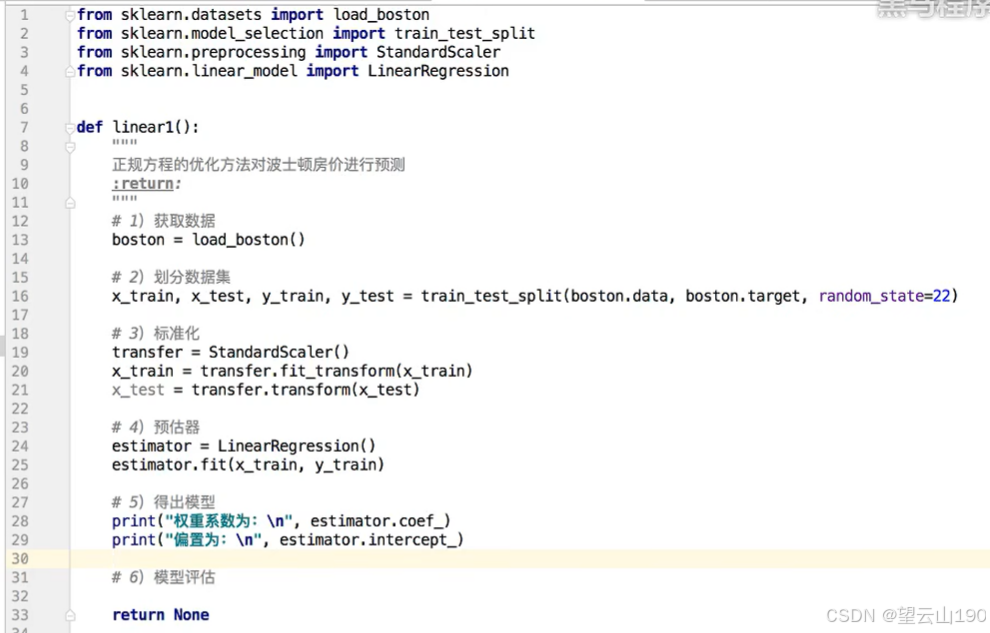
4.1.4 波士顿房价预测

流程：

1）获取数据集

2）划分数据集

3）特征工程：无量纲化-标准化

4）预估器流程：fit--> 模型

                          coef_ intercept

5) 模型评估

回归性能评估：

对比：