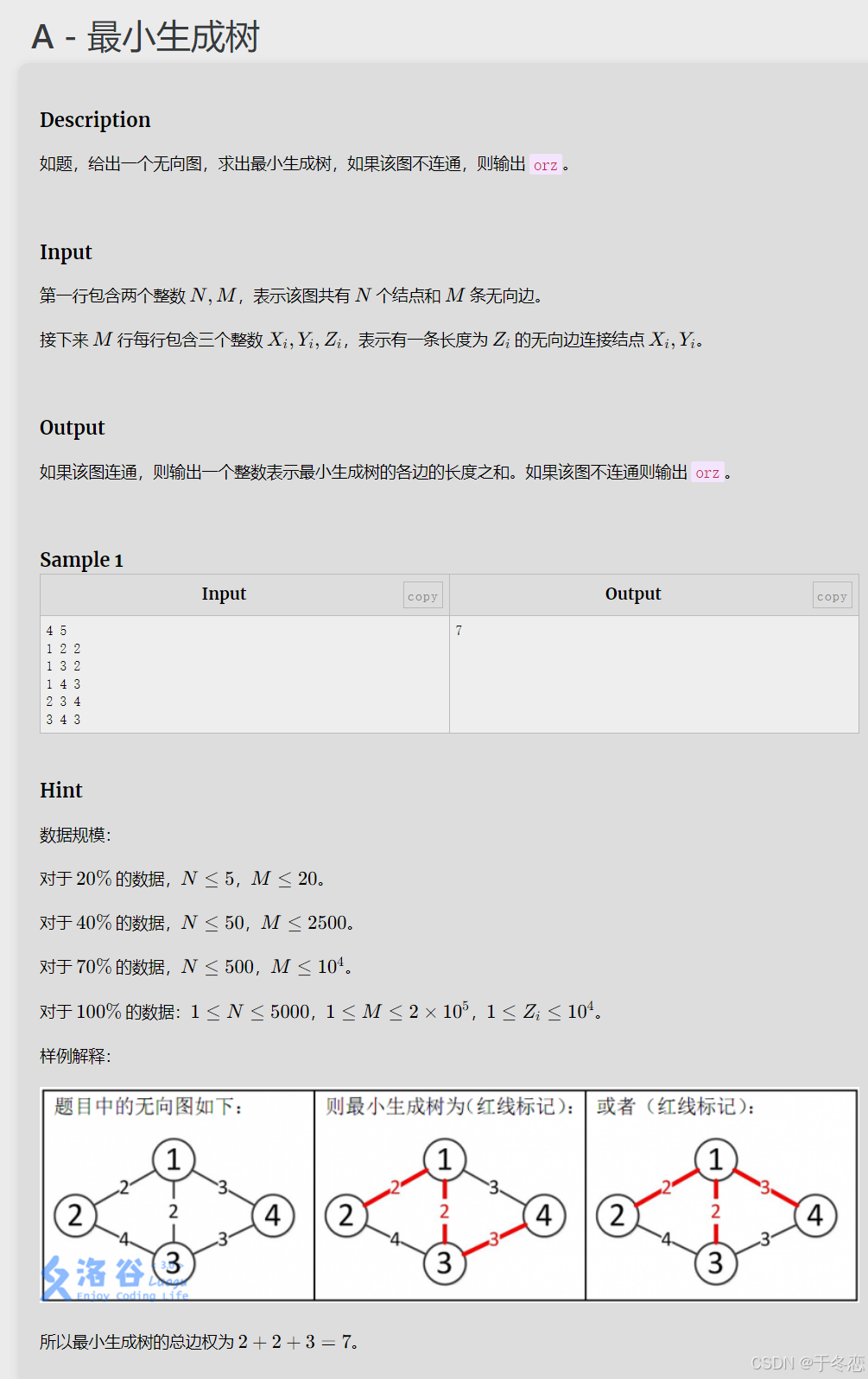
该题用Kruskal算法可以写出（因为我只会这个算法的实现）

每次选择一条权值最小的边，使这条边的两头连通（原本已经连通的就不选），直到所有结点都连通

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n, m, i, j, u, v, total;
struct node {
	int start, to;
	long long edge;
}bian[10000000];//结构体数组
int f[1000000];
long long ans;
//结构体的排序会用到
bool cmp(node a, node b) {
	return a.edge < b.edge;
}
//并查集
int find(int x) {
	if (f[x] == x)return x;
	else return f[x] = find(f[x]);
}
void tree() {
	for (int i = 1; i <= m; i++) {
		int u = find(bian[i].start);
		int v = find(bian[i].to);
		if (u == v)continue;//因为不可成环，故相等时跳过
		ans += bian[i].edge;
		f[u] = v;//若不在一个集合则合并为一个集合
		total++;//计算连通的点数
		if (total == n - 1)break;
	}
}

int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)f[i] = i;
	for (int i = 1; i <= m; i++) {
		cin >> bian[i].start >> bian[i].to >> bian[i].edge;
	}
	sort(bian + 1, bian + m + 1, cmp);//从小到大排序
	tree();
	if (total == n - 1)
		cout << ans;
	else cout << "orz";
	return 0;
}

 再看几个相似的题目

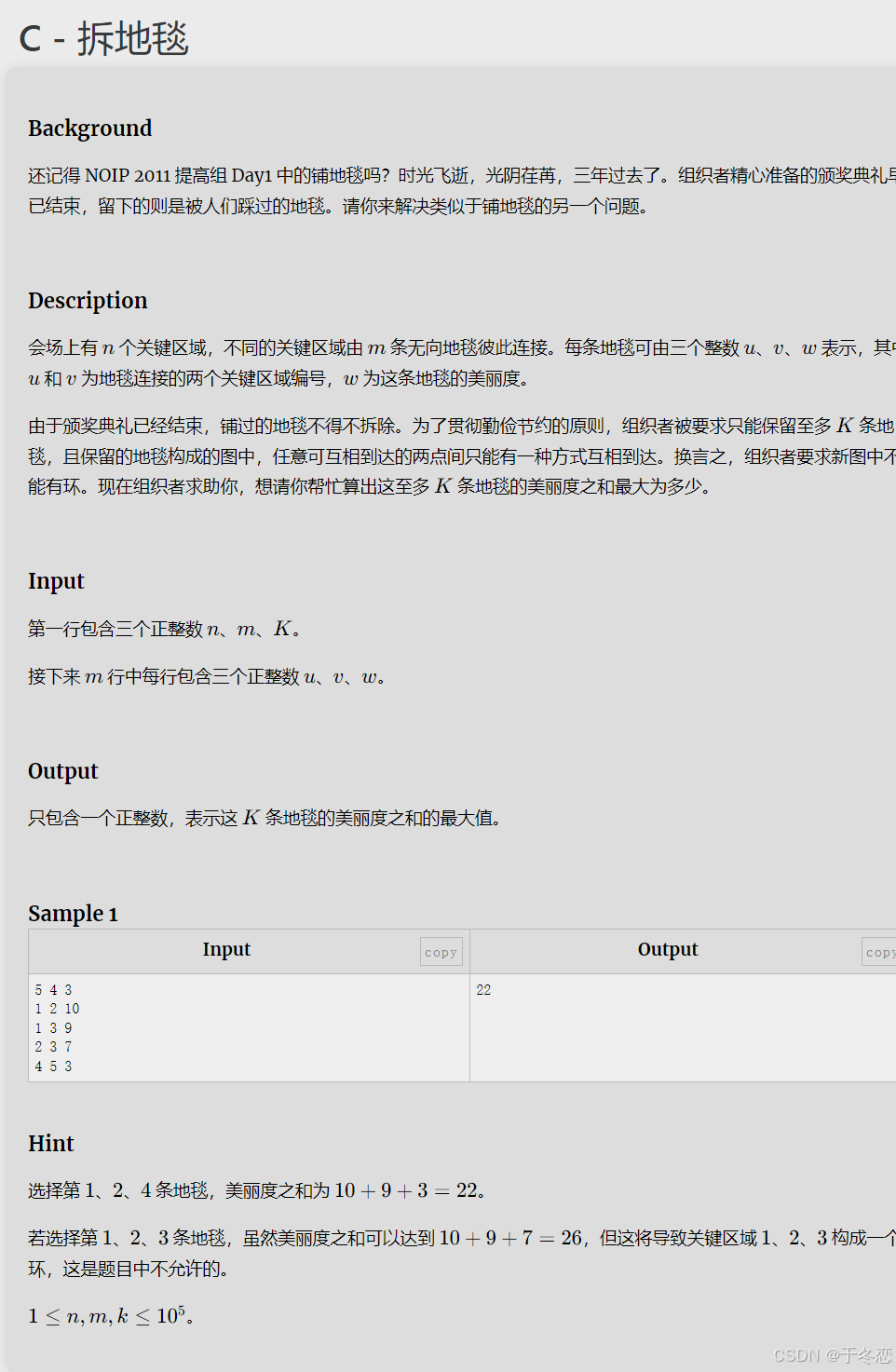
 简直如出一辙，不过一个是求小生成树，一个是最大生成树且多增一个条件至多k条

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n, m, i, j, u, v, k,total;
struct node {
	int start, to;
	long long edge;
}bian[10000000];
int f[1000000];
long long ans;
bool cmp(node a, node b) {
	return a.edge > b.edge;
}
int find(int x) {
	if (f[x] == x)return x;
	else return f[x] = find(f[x]);
}
void tree() {
	int kk = 0;
	for (int i = 1; i <= m; i++) {
		int u = find(bian[i].start);
		int v = find(bian[i].to);       
		if (u != v) {
			ans += bian[i].edge;
			f[u] = v;
			total++;
			kk++;
		}
		if (kk > n - 1 && total == n - 1)break;
		if (kk <= n - 1 && total == k)break;
	}
}

int main()
{
	cin >> n >> m>>k;
	for (int i = 1; i <= n; i++)f[i] = i;
	for (int i = 1; i <= m; i++) {
		cin >> bian[i].start >> bian[i].to >> bian[i].edge;
	}
	sort(bian + 1, bian + m + 1, cmp);
	tree();
		cout << ans;
	return 0;
}

此题为结束条件不同

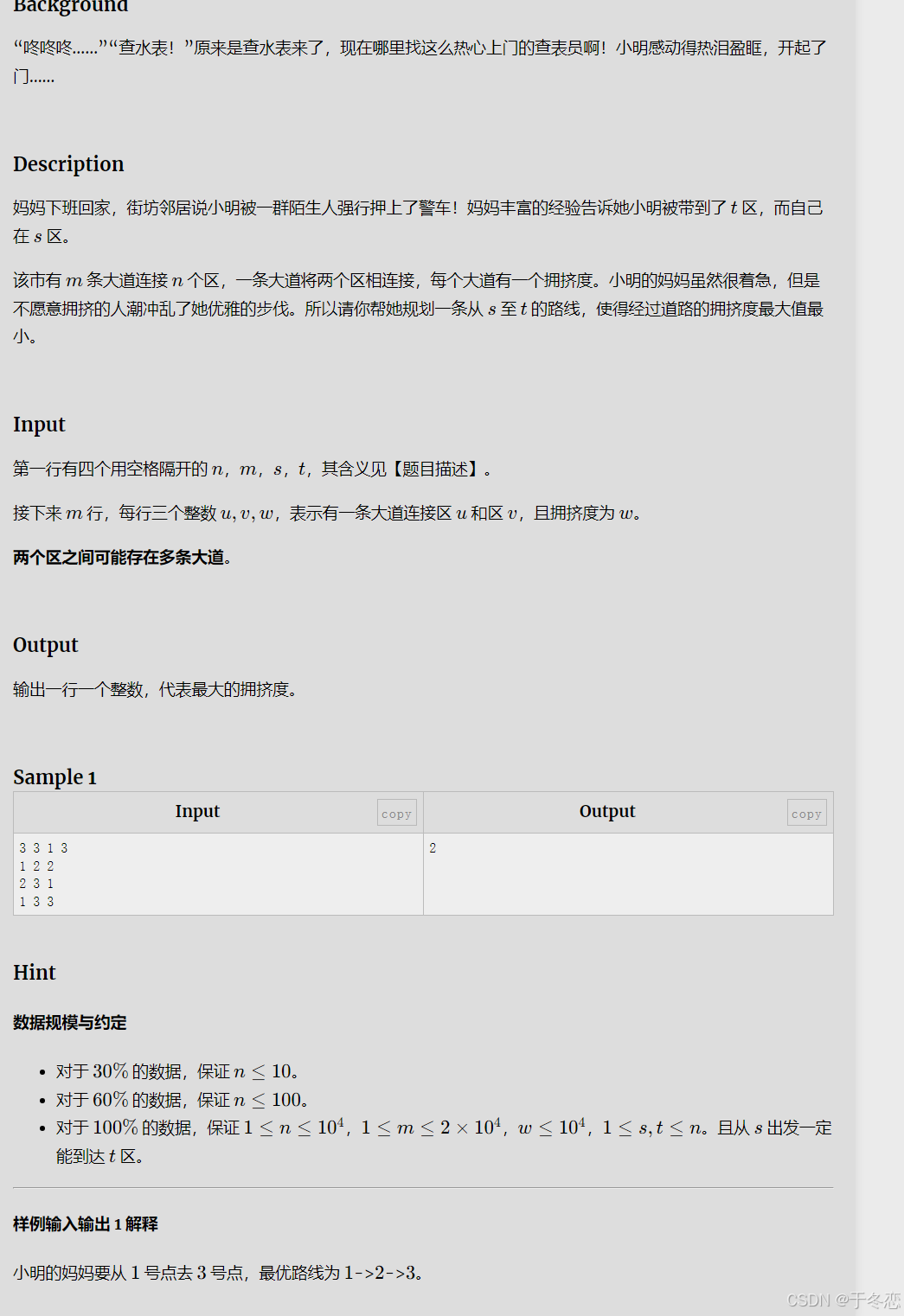
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int n, m, i, j, u, v, s, t,total;
struct node {
	int start, to;
	long long edge;
}bian[10000000];
int f[1000000];
bool cmp(node a, node b) {
	return a.edge < b.edge;
}
int find(int x) {
	if (f[x] == x)return x;
	else return f[x] = find(f[x]);
}

int main()
{
	cin >> n >> m>>s>>t;
	for (int i = 1; i <= n; i++)f[i] = i;
	for (int i = 1; i <= m; i++) {
		cin >> bian[i].start >> bian[i].to >> bian[i].edge;
	}
	sort(bian + 1, bian + m + 1, cmp);
	for (int i = 1, total = 0; i <= m && total <= n - 1; i++) {
		int u = find(bian[i].start);
		int v = find(bian[i].to);
		if (u != v) {
			f[u] = v;
			total++;
		}
		if (find(s) == find(t)) {
			cout << bian[i].edge;
			return 0;
		}
	}
	return 0;
}