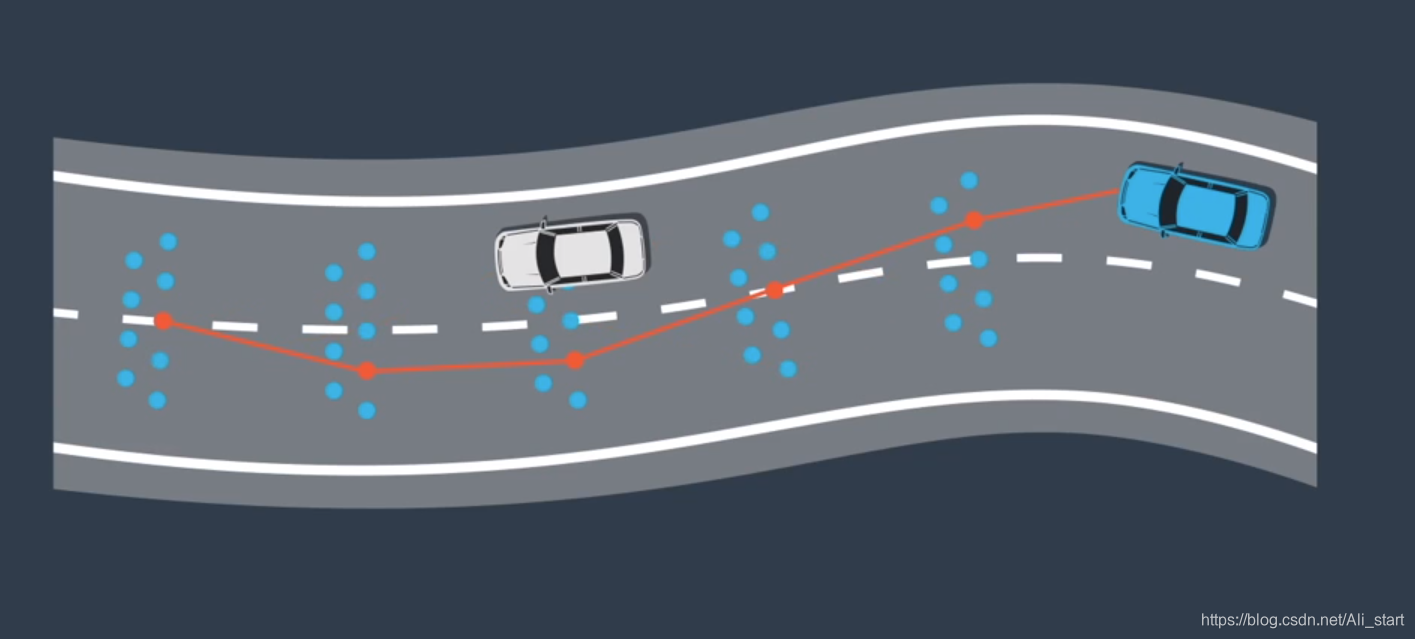
在规划中 我们通过结合高精度地图,定位和预测来构建车辆轨迹,
第一步是路线规划,地图路线导航,从 A 前往 B, Apollo 中 通过路线规划模块处理该任务,
第二步是轨迹规划,目标是生成免碰撞和舒适的可执行轨迹,该轨迹由一系列点定义,每个点都有一个关联速度,和一个指示何时应抵达那个点的时间戳
路线规划(路由)
路线规划三个输入:
第一个输入为地图,Apollo 提供的地图数据包括公路网和实时交通信息
第二个输入为我们当前在地图上的位置(A)
第三个输入为我们的目的地(B)
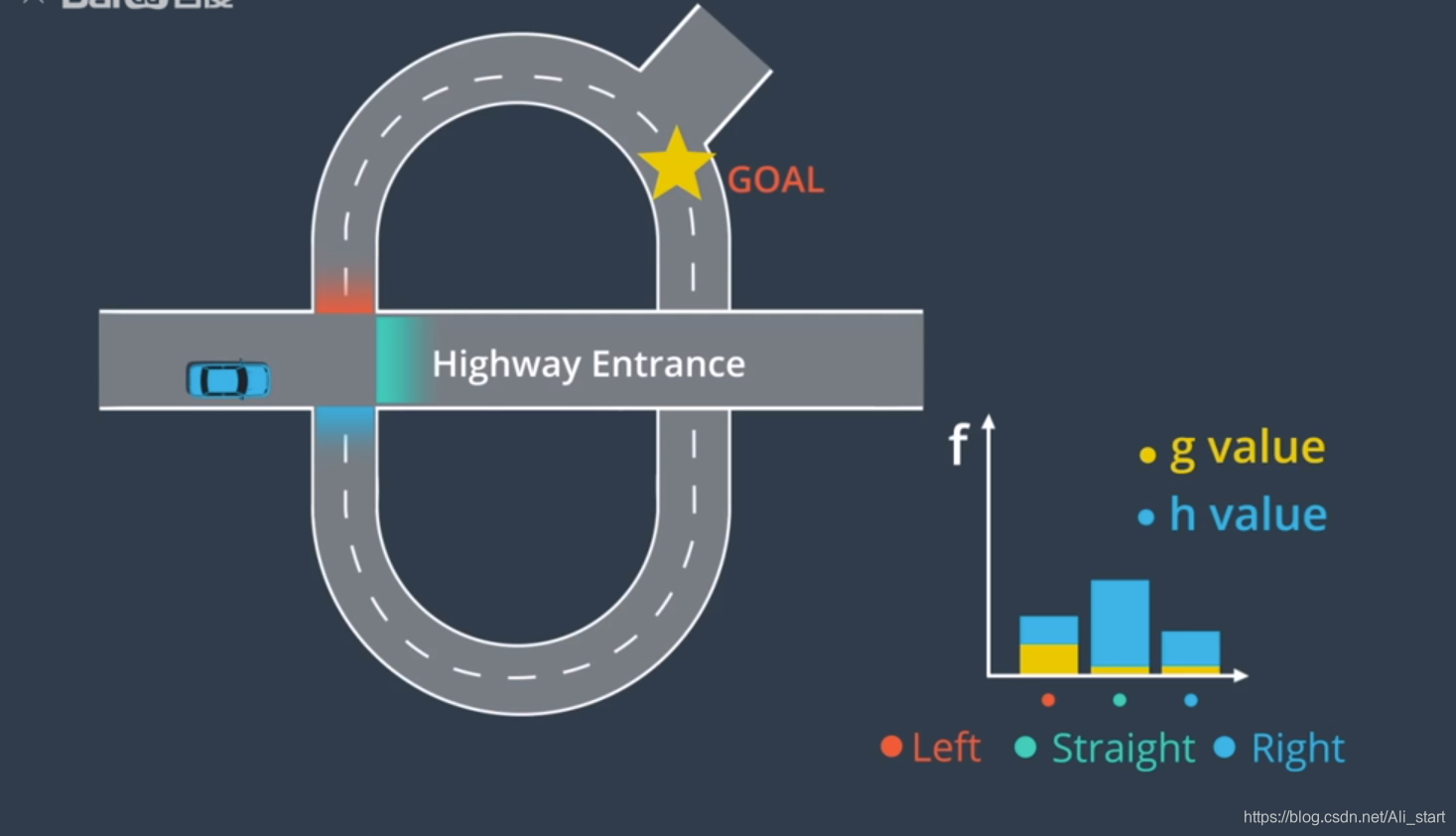
地图数据转化为“图“(graph)——包括节点和边
图映射到网格世界(橘黄色点到绿色点) A*算法

g是起点到候选节点的值
h是候选节点到终点的值
f是两者结合 然后选择最小
轨迹生成
轨迹生成的目标是生成由一系列路径点所定义的轨迹,为每个路径点分配了一个时间戳和速度,我们让一条曲线与这些路径点拟合,生成轨迹的几何表征。然后多条轨迹选最佳
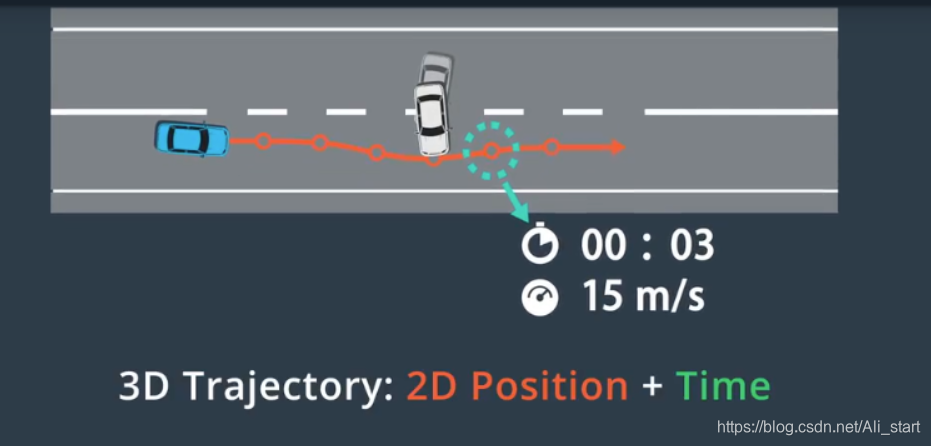
由于移动的障碍物可能会暂时阻挡部分路段,轨迹中的每个路点都有时间戳,我们可以将时间戳与预测模块的输出相结合,以确保在我们计划通过时,轨迹上的每个路径点均未被占用,这些时间戳创建了一个三维轨迹,每个路径点由空间中的两个维度,以及时间上的第三个维度来定义,我们还为每个路径点指定了一个速度,速度用于确保车辆按时到达每个路径点
1.多种约束条件
- 轨迹应能免于碰撞
- 要让乘客感到舒适 路径点之间的过渡以及速度的任何变化都必须平滑
- 可行的实际路径
- 交通规则
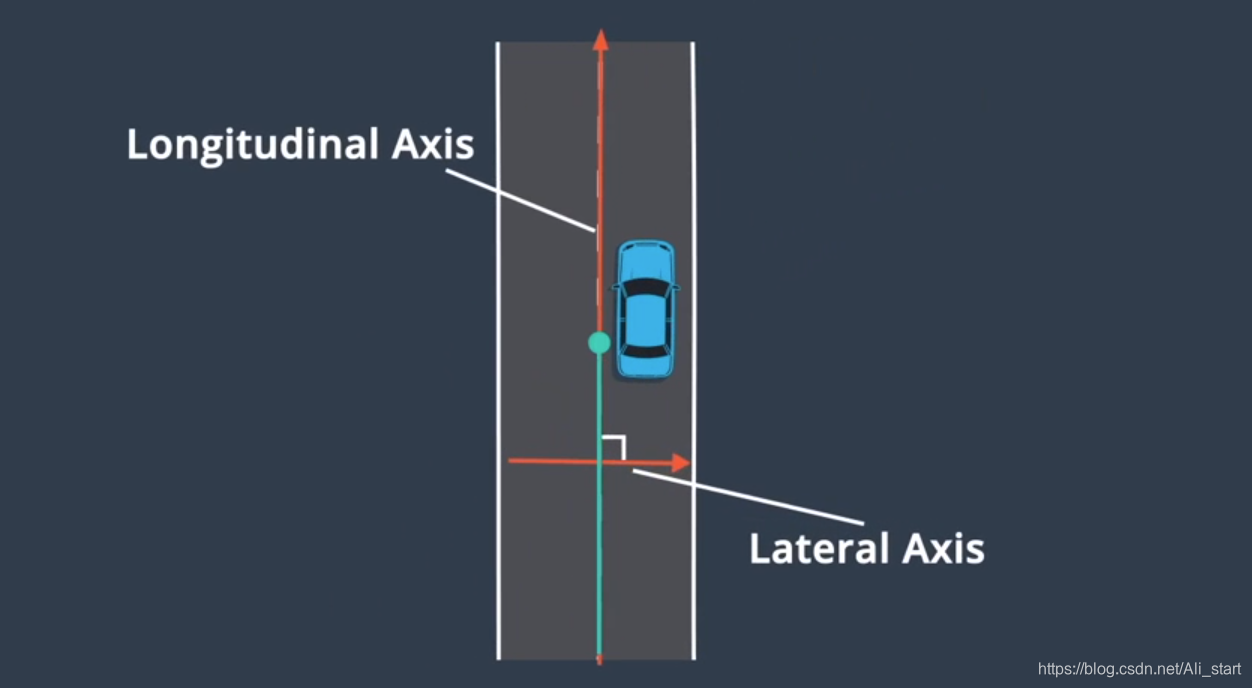
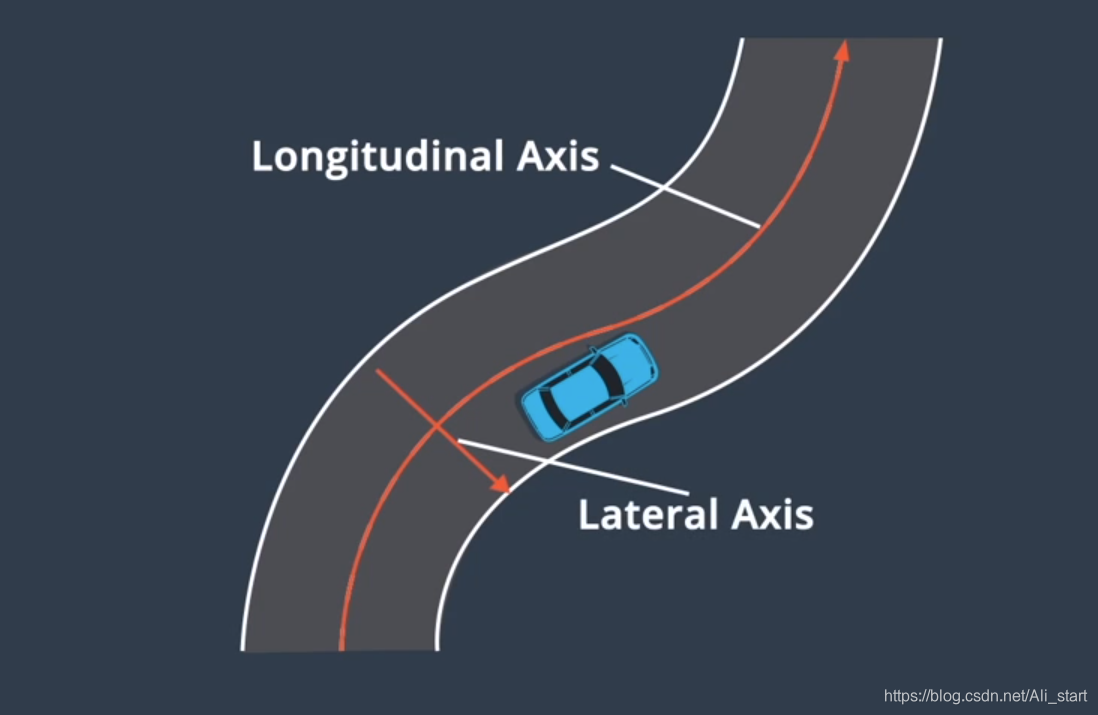
2.Frenet坐标系
路中心线为y轴,距中心线平移的距离为x轴
3.路径-速度解耦 规划
将轨迹分为两步:
- 路径规划
- 速度规划
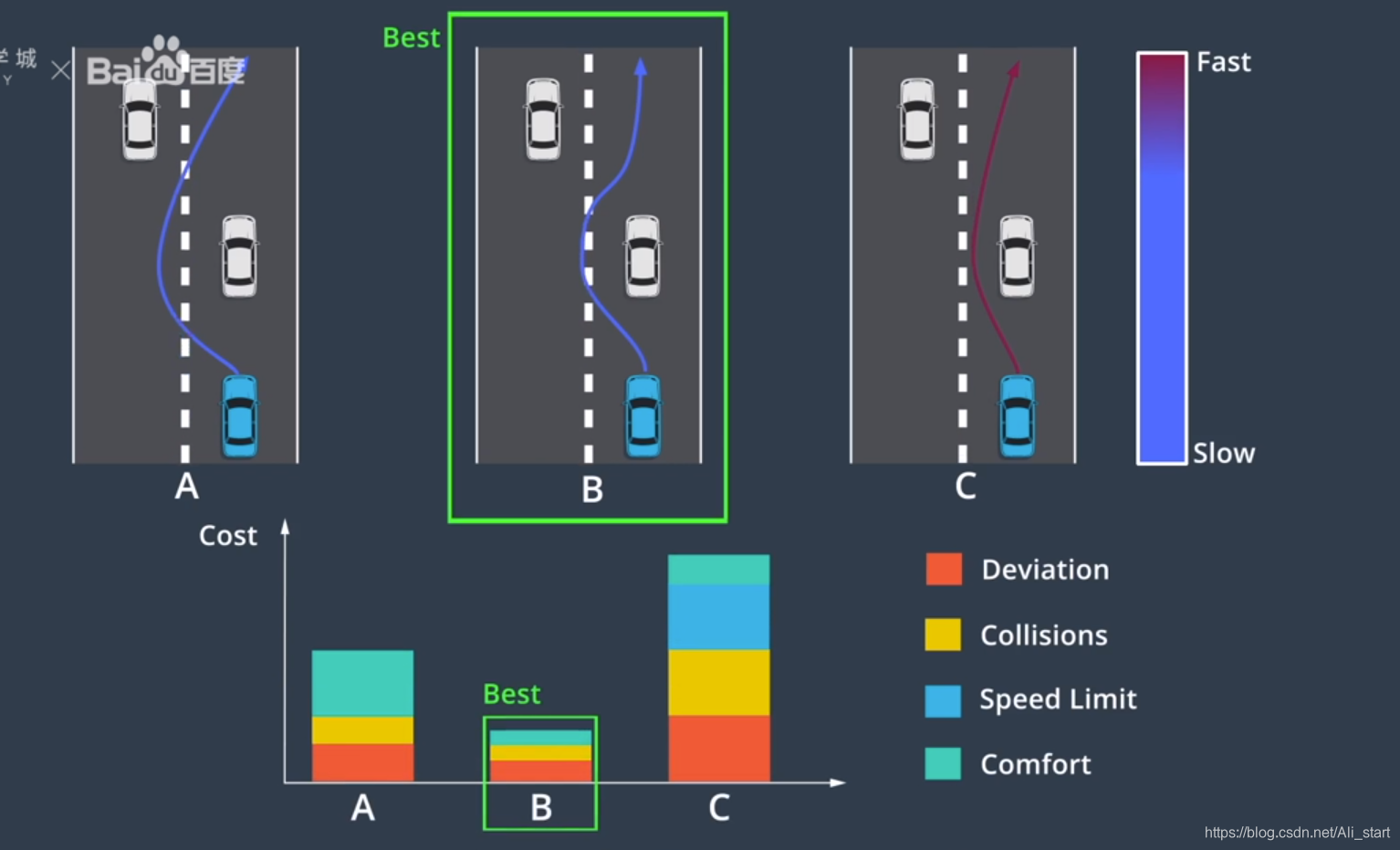
路段分割成单元格,然后对这些单元格中的点进行随机采样,通过从每个单元格中取一个点并将点连接,我们创建了候选路径,通过重复此过程 我们可以构建多个候选路径,我们使用成本函数对这些路径进行评估,并选择成本最低的路径,成本函数可能考虑以下因素,与车道中心的偏离,与障碍物的距离,速度和曲率的变化,对车辆的压力,或任何其他因素。

---------------------
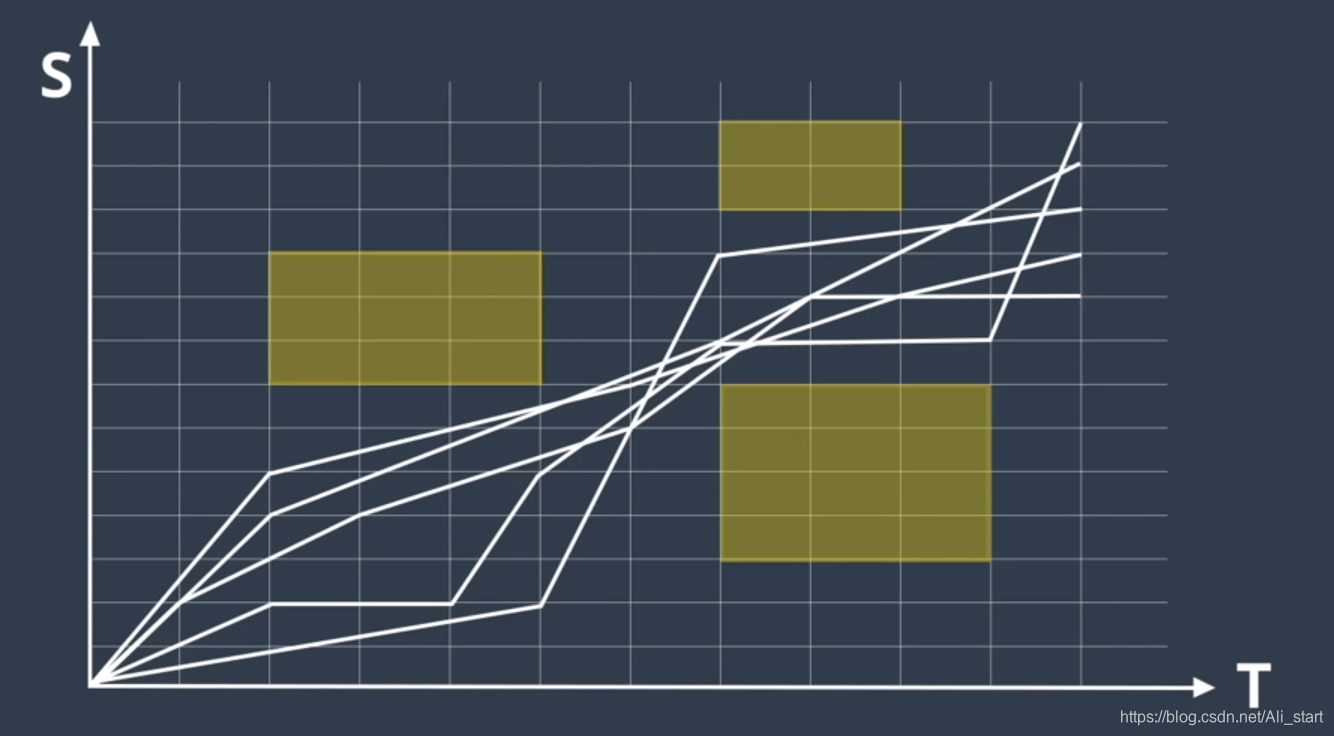
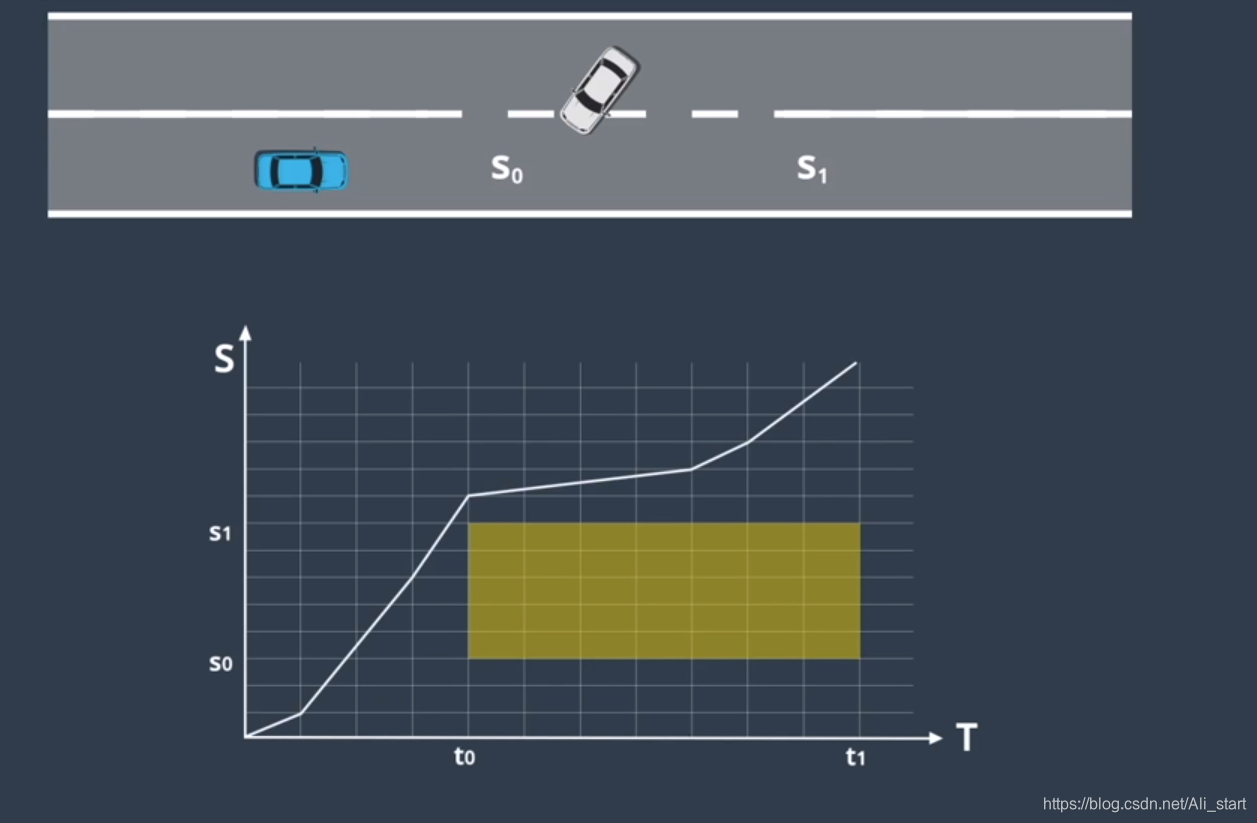
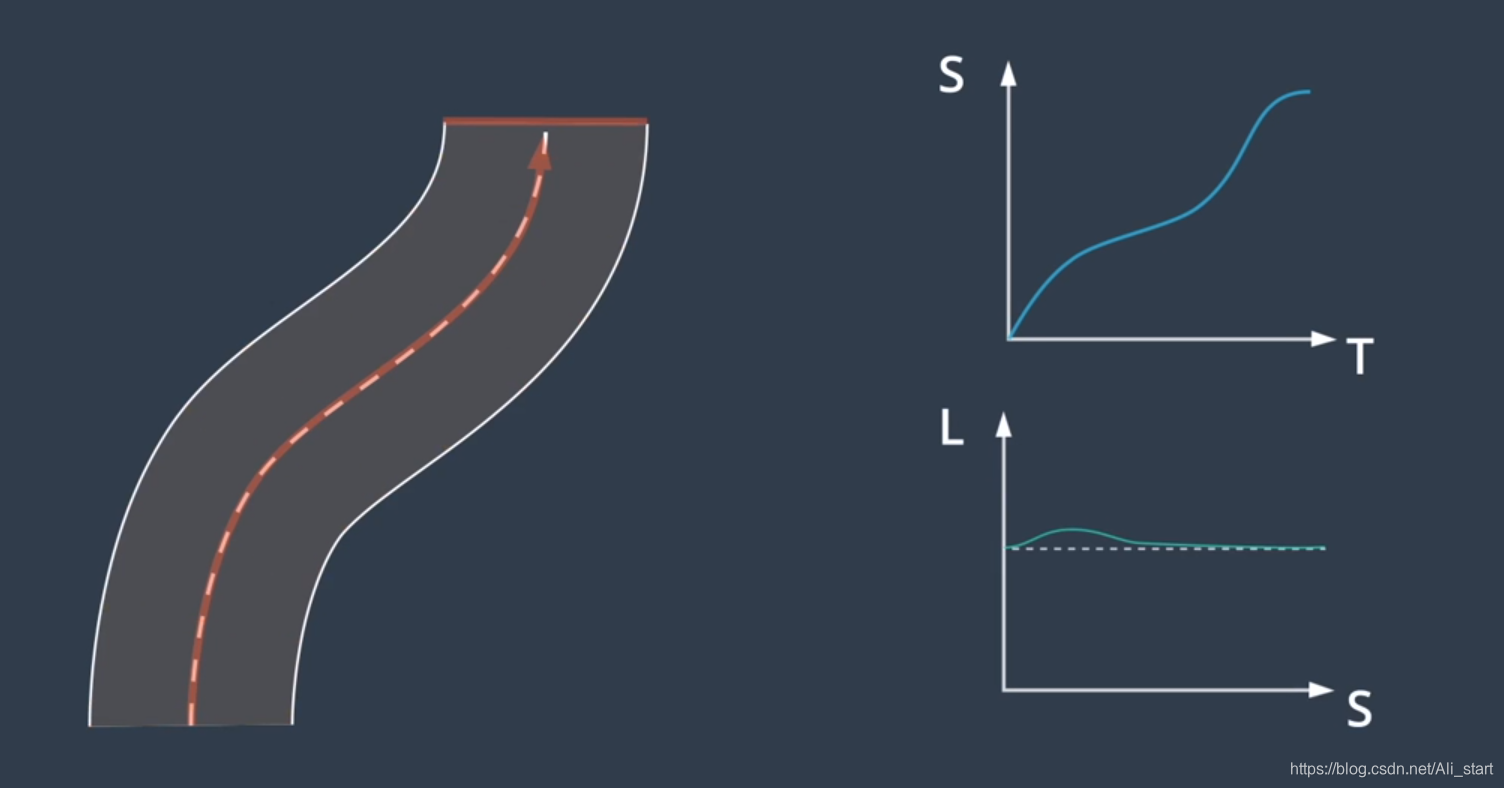
然后选择与该路径关联的速度曲线,一个被称为“ST 图”的工具可以帮助我们设计和选择速度曲线,在 ST 图中,“s”表示车辆的纵向位移 、“t”表示时间,ST 图上的曲线是对车辆运动的描述,因为它说明了车辆在不同时间的位置,由于速度是位置变化的速率,所以我们可以通过查看曲线的斜率从 ST 图上推断速度,斜坡越陡
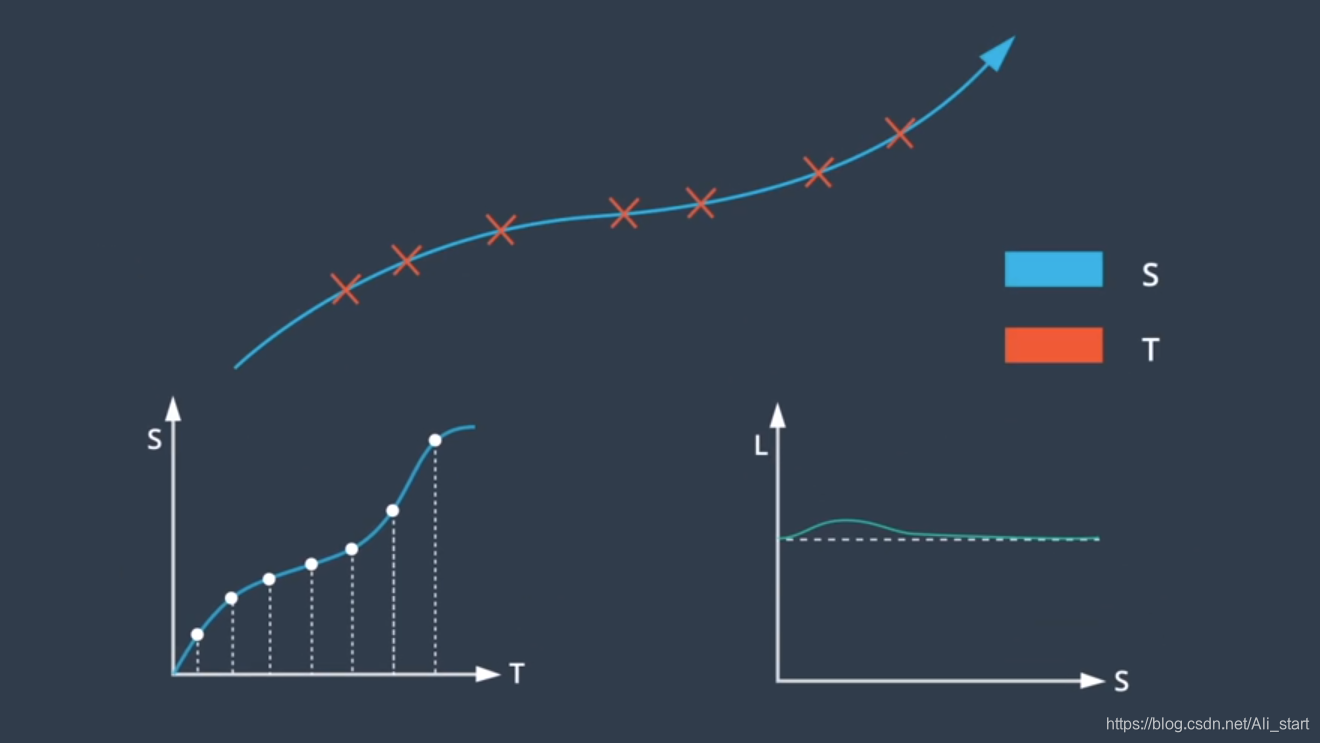
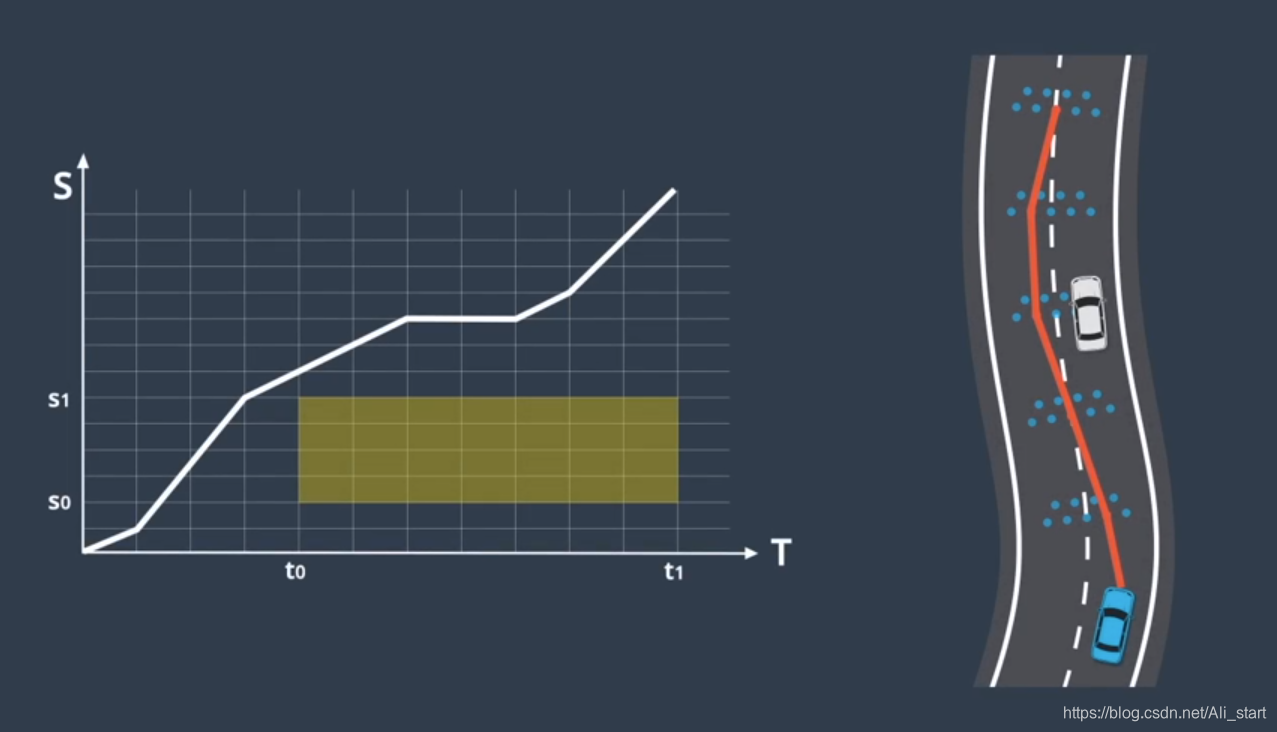
最佳速度曲线,我们需要将 ST 图离散为多个单元格,单元格之间的速度有所变化,但在每个单元格内 速度保持不变,该方法可简化速度曲线的构建,并维持曲线的近似度,在 ST 图中,可以将障碍物绘制为在特定时间段内,阻挡道路的某些部分的矩形,例如 假设预测模块预测车辆,将在 t0 到 t1 的时间段内驶入我们的车道,由于该车将在此期间占据位置 s0 到 s1,因此我们在 ST 图上绘制了一个矩形,它将在时间段 t0 到 t1 期间阻挡位置 s0 到 s1,为避免碰撞,速度曲线不得与此矩形相交,既然有了一张各种单元格被阻挡的 ST 图,我们便可以使用优化引擎为该图选择最佳的速度曲线,优化算法通过复杂的数学运算来搜索,受到各种限制的低成本解决方案,这些限制可能包括:交通规则限制 ,距离限制 如与障碍物的距离,汽车的物理限制 如加速度限制
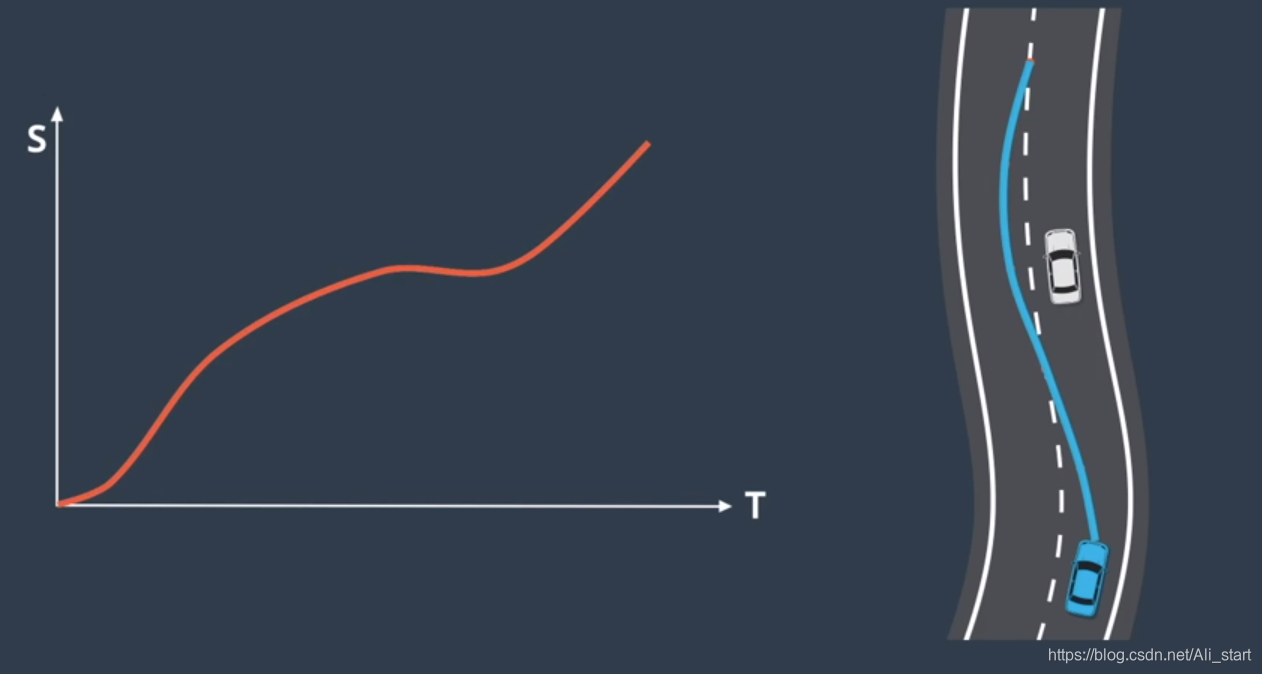
为了将离散解决方案转换为平滑轨迹,我们可使用“二次规划”技术,二次规划将平滑的非线性曲线与这些分段式线性段拟合
4.三维轨迹生成Lattice
一旦路径和速度曲线就绪,我们便可以用其构建三维轨迹。。。。就是再加一个时间的维度
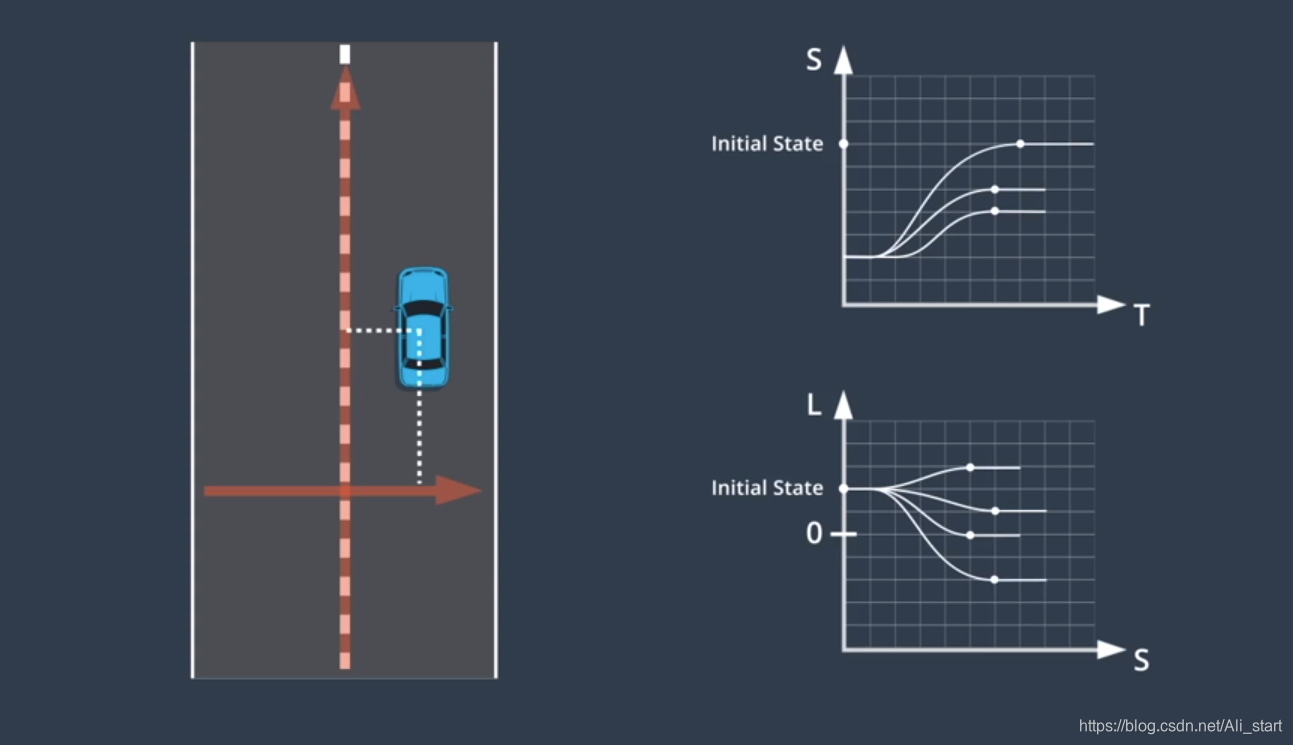
通过分离轨迹的纵向和横向分量来解决的,将三维问题分解成两个单独的二维问题
- 其中一个二维轨迹是具有时间戳的纵向轨迹,我们称之为 ST 轨迹,
- 另一个二维轨迹是,相对于纵向轨迹的横向偏移,我们称之为 SL 轨迹
- 然后将它们合并
为生成纵向和横向二维轨迹,我们先将初始车辆状态投射,到 ST 坐标系和 SL 坐标系中,通过对预选模式中的多个候选最终状态进行采样,我们来选择最终车辆状态,对于每个候选最终状态,我们构建了一组轨迹,将我们的车辆从其初始状态转换为最终状态,我们使用成本函数对这些轨迹进行评估,并选择成本最低的轨迹
5.车辆状态
- 巡航:车辆将在完成规划步骤后定速行驶
- 跟随:尝试在时间 t 出现在某辆车后面 跟随车辆
- 停止:速度和加速度会被修正为 0
一旦我们同时拥有了 ST 和 SL 轨迹,我们就需要将它们重新转换为笛卡尔坐标系,然后 可以将它们相结合,构建由二维路径点和一维时间戳组成的三维轨迹,ST 轨迹是随时间变化的纵向位移,SL 轨迹是,纵向轨迹上每个点的横向偏移,由于两个轨迹都有纵坐标 S,所以我们可以通过将其 S 值进行匹配来合并轨迹