洛谷 CF1733E Conveyor

题目分析

在（0,0）格，每一秒都生成一只史莱姆，每只史莱姆每秒都向右或向下一格，可见，每只史莱姆的位置（x，y）与当前时间t，它出生时间t'满足：

$x+y=t-t'$

其中，每只史莱姆的出生时间t'不同，所以不可能有两只史莱姆撞在一起，所以不需要考虑相撞的情况。

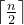
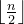
对于每格子，如果它是第奇数次被史莱姆到达，那么下一秒史莱姆将会去它右边那一格；反之，则会去它下边那格。换而言之，如果一个格子被访问了n次，则有 $\left \lceil \frac{n}{2} \right \rceil$ 次去右边， $\left \lfloor \frac{n}{2} \right \rfloor$ 次去下面。并且，在第t秒，第（0,0）格被访问了 t + 1 次。于是，可以根据时间 t，推导出第（0,0）格被访问的次数，然后用dp的思想推出（x,y）格被访问的次数，其中，dp的状态转移方程：

$dp[i][j]=\left \lceil \frac{dp[i - 1][j]}{2} \right \rceil+\left \lfloor \frac{dp[i][j-1]}{2} \right \rfloor$

但是，如果一个史莱姆恰好在第 t 秒到达（x - 1,y），下一秒才能到达（x,y），此时我们计算的dp[x][y]的值是存在误差的，即不是所有的史莱姆都能在 t 秒到达（x,y）。为了保证，计算dp[x][y]的精确性，应当对dp的定义做出修改：dp[i][j]表示在 t 秒内能到达（x,y）的史莱姆数量，那么，dp[0][0]的初值不应该为 t 秒内经过(0,0)的史莱姆数量 t + 1，而应该为 t 秒内能到达（x,y）的史莱姆数量 t - x - y + 1。

用第 t 秒（x,y）格访问的次数减去第 t - 1 秒（x,y）格访问的次数，如果为0，则证明第 t 秒内没有史莱姆访问，也就是无史莱姆，反之，就是有史莱姆。

代码实现

#include <iostream>
#include <vector>
#include <cmath>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
long long dp1[120][120], dp2[120][120];
long long t, x, y, q, _x, _y;
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> q;
    while (q--) {
        cin >> t >> x >> y;
        memset(dp1, 0, sizeof(dp1));
        memset(dp2, 0, sizeof(dp2));
        dp1[0][0] = max(t - x - y + 1,(long long)0);//t秒内能到达(x,y)的有效次数，最小为0
        dp2[0][0] = max(t - x - y, (long long)0);//t-1秒内能达到(x,y)的有效次数，最小为0
        for (int i = 0; i < 120; i++) {//dp求次数
            for (int j = 0; j < 120; j++) {
                if (i < 119) {
                    dp1[i + 1][j] += (dp1[i][j]) >> 1;//偶数次下移，应向下取整
                    dp2[i + 1][j] += (dp2[i][j]) >> 1;
                }
                if (j < 119) {
                    dp1[i][j + 1] += (dp1[i][j] + 1) >> 1;//奇数次右移，应向上取整
                    dp2[i][j + 1] += (dp2[i][j] + 1) >> 1;
                }
            }
        }
        if (dp1[x][y] == dp2[x][y])cout << "NO\n";//第t秒与第t-1秒相同，说明没有史莱姆
        else cout << "YES\n";//反之，有史莱姆
    }
}