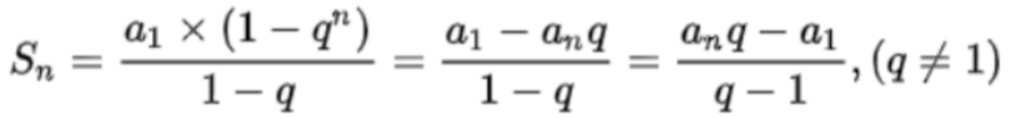一、堆的概念
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵 完全二叉树的 数组对象。 堆是非线性数据结构,相当于一维数组,有两个直接后继。
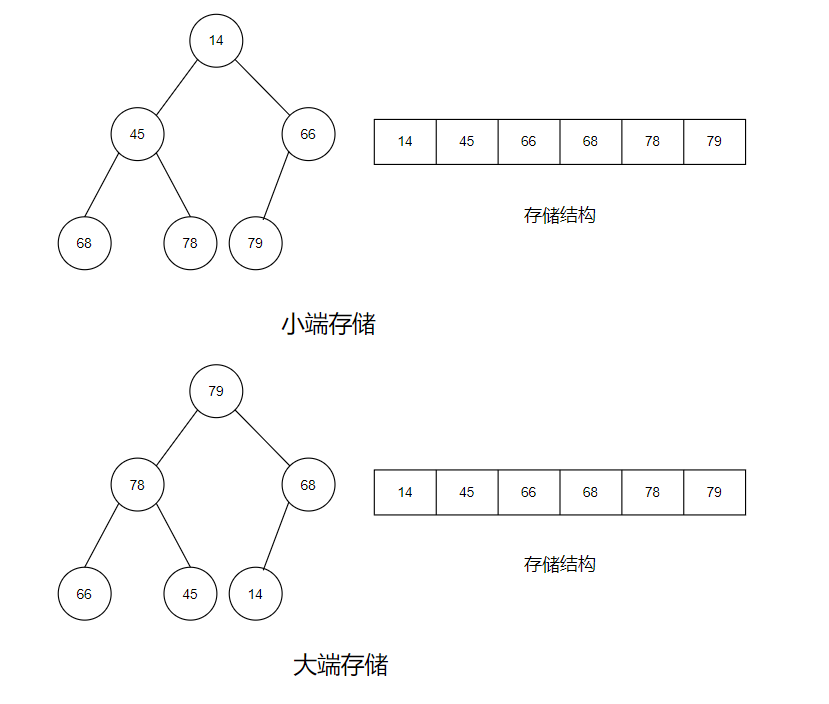
如果有一个关键码的集合K = { k₀,k₁,k₂ ,k₃ ,…,kₙ₋₁ },把它的所有元素按完全二叉树的顺序存储方式存储,在一个一维数组中,并满足:Kᵢ <= K₂ *ᵢ₊₁ 且 Kᵢ <= K₂ *ᵢ₊₂ (Kᵢ >= K₂ *ᵢ₊ ₁ 且 Kᵢ >= K₂ *ᵢ₊₂ ) i = 0,1,2…,则称为小堆 (或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
【大根堆和小根堆】:
根结点最大的堆叫做大根堆,树中所有父亲都大于或等于孩子。
根结点最小的堆叫做小根堆,树中所有父亲都小于或等于孩子。
共同特点:父亲 =(孩子-1)/2
大堆小堆有什么特点呢?
我们购物平台中,我想选择销量大的前k家,这个时候,我们不需要对所有的数据进行排序,只需要取出前k家最大的值就可以。而最值常常出现在0号位,我们就可以利用Topheap解决,大大减少了我们的时间复杂度;
特点:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
- 每层节点个数为2^(h-1)个
二、堆的创建
1、头文件的声明:
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}Heap;
void HeapInit(Heap* hp);
// 堆的销毁
void HeapDestory(Heap* hp);
void swap(HPDataType* p1, HPDataType* p2);
void AdjustUp(HPDataType* a, int child);
void AdjustDown(HPDataType* a, int n, int parent);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);2、代码实现:
2.1堆的初始化与堆的摧毁
//堆的初始化
void HeapInit(Heap* hp) {
assert(hp);
hp->a = NULL;
hp->capacity = hp->size = 0;
}
//堆的摧毁
void HeapDestory(Heap* hp) {
assert(hp);
free(hp->a);
hp->a = NULL;
hp->capacity = hp->size = 0;
}2.2堆的插入
具体步骤如下:
1.将新插入的元素放置在堆的最后一个位置(通常是数组的末尾)。
2.将该元素与其父节点进行比较。
3.若该元素大于(或小于,具体根据堆是最大堆还是最小堆而定)其父节点的值,则交换该元素和其父节点的位置。
4.继续向上对比和交换,直到满足堆的性质或达到堆的根节点。
// 堆的插入
void HeapPush(Heap* hp, HPDataType x) {
assert(hp);
//与顺序表的开辟类似
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
//使用三目操作符开辟空间大小
HPDataType* tmp = (HPDataType*)realloc(hp->a, newcapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->size++;
hp->a[hp->size] = x;
//向上调整法,因为每次的插入是在数组末尾
//每次插入需要与父亲比较大小交换
AdjustUp(hp->a, hp->size - 1);
}2.2.1向上调整法
//向上调整法,因为每次的插入是在数组末尾
//每次插入需要与父亲比较大小交换
AdjustUp(hp->a, hp->size - 1);
我们每次插入末尾的位置,相当于孩子,我们需要找到该孩子的父亲与之比较大小,这个时候就要利用堆的特点:父亲 =(孩子-1)/2
向上调整法:
void AdjustUp(HPDataType* a, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (a[child] < a[parent]) {
//根据要求设置大端小端
swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else{
break;
}
}
}交换函数:
因为在堆的实现中我们会经常使用父子交换
void swap(HPDataType* p1, HPDataType* p2) {
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
//这里也可以回想前面学习
//不使用第三个变量,利用换位与实现交换
}2.4堆的删除
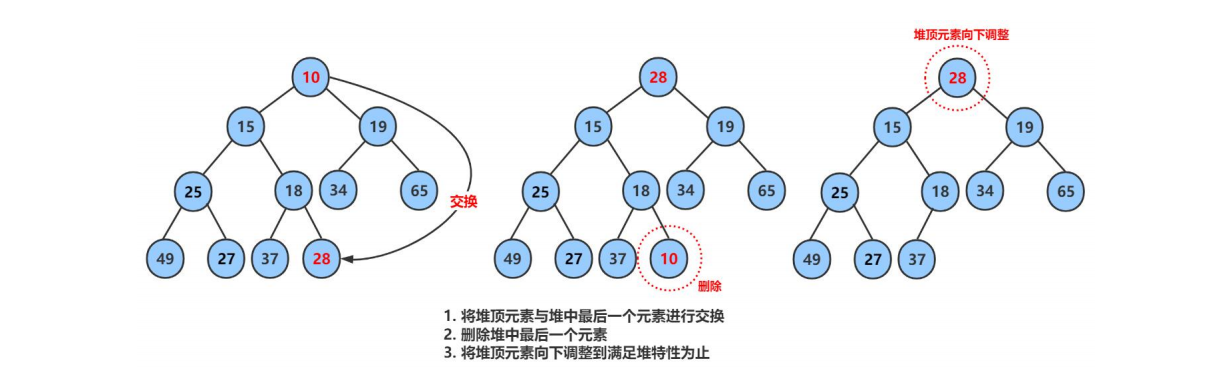
如果我们直接删除堆顶数据,将数组数据整体向前移动,这样会导致堆的乱序;
删除堆是删除堆顶的数据,将堆顶的数据根最后一个数据一换,然后删除数组最后一个数据,再进行向下调整算法。
2.4.1向下调整法
void AdjustDown(HPDataType* a, int n, int parent) {
//注:这里的parent为0,而数组a则是首尾交换的
int child = parent * 2 + 1;
//假设左孩子小
while (child < n) {
//while循环直到超出数组长度
//左孩子大
if (a[child] > a[child + 1]) {
child++;
}
if (a[child]>a[parent]) {
swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
}
}这样我们只需要完成交换,传指就可以了
void HeapPop(Heap* hp) {
assert(hp);
assert(hp->size);
swap(&hp->a[0], &hp->a[hp->size - 1]);
hp->size--;
AdjustDown(hp->a, hp->size, 0);
}
3、总结
升序:建大堆
降序:建小堆
(1)升序:建大堆
【思考】排升序,建小堆可以吗?-- 可以(但不推荐)。
首先对 n 个数建小堆,选出最小的数,接着对剩下的 n-1 个数建小堆,选出第二小的数,不断重复上述过程。
【时间复杂度】建 n 个数的堆时间复杂度是 O(N),所以上述操作时间复杂度为 O(N²),效率太低,关系变得杂乱,尤其是当数据量大的时候,效率就更低。同时堆的价值也没有被体现出来,这样不如用直接排序。
排升序,因为数字依次递增,需要找到最大的数字,得建大堆。
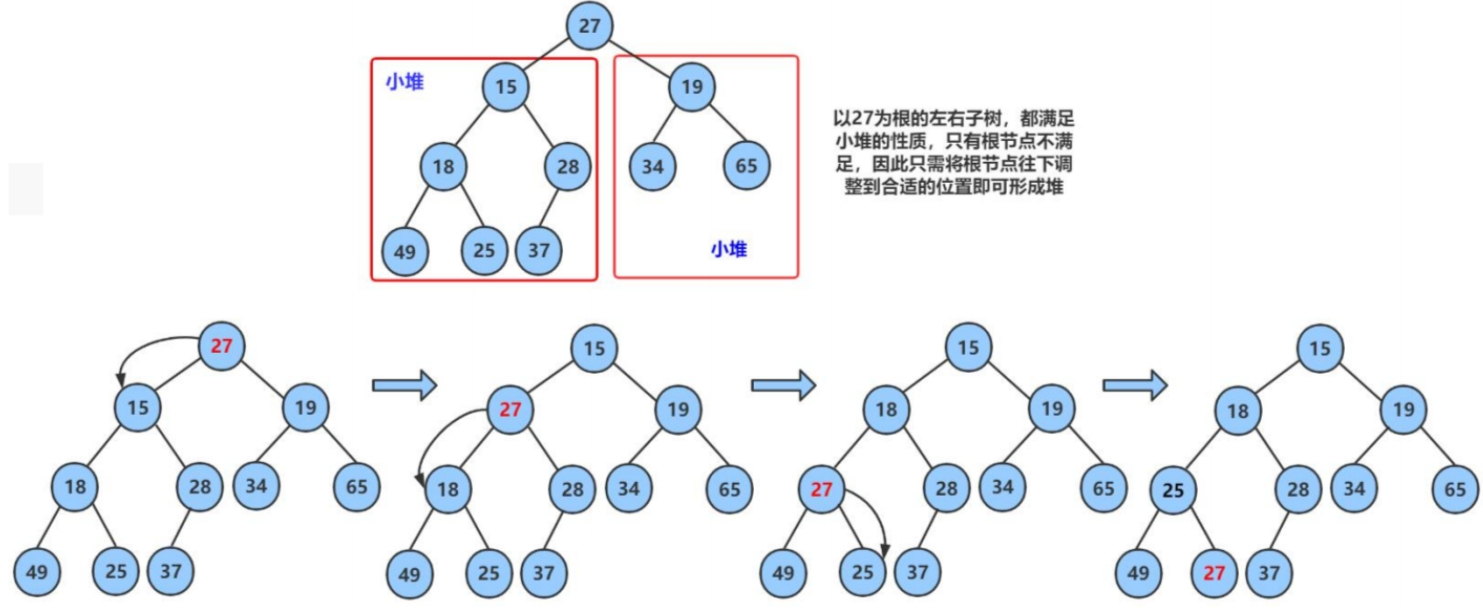
首先对 n 个数建大堆。将最大的数(堆顶)和最后一个数交换,把最大的数放到最后。前面 n-1 个数的堆结构没有被破坏(最后一个数不看作在堆里面的),根节点的左右子树依然是大堆,所以我们进行一次向下调整成大堆即可选出第 2 大的数,放到倒数第二个位置,然后重复上述步骤。
【时间复杂度】:建堆时间复杂度为 O(N),向下调整时间复杂度为 O(log₂N),这里我们最多进行N-2 次向下调整,所以堆排序时间复杂度为 O(N*log₂N),效率相较而言是很高的。
因为在堆的实现中我们会经常使用父子交换
void swap(HPDataType* p1, HPDataType* p2) {
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
//这里也可以回想前面学习
//不使用第三个变量,利用换位与实现交换
}我相信接下来对你来说简直轻而易举
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);4.1取堆顶数据
HPDataType HeapTop(Heap* hp) {
assert(hp);
assert(hp->size);
return hp->a[0];
}4.2 堆的数据个数
int HeapSize(Heap* hp) {
assert(hp);
assert(hp->size);
return hp->size;
}4.3堆的判空
int HeapEmpty(Heap* hp) {
assert(hp);
assert(hp->size>0);
//为NULL,返回1,不为NULL,返回0;
return hp->size == 0 ? 1 : 0;
}5、堆的时间复杂度
5.1建堆的时间复杂度
5.1.1向下调整法建堆
// 堆的插入
void HeapPush(Heap* hp, HPDataType x) {
assert(hp);
//与顺序表的开辟类似
if (hp->size == hp->capacity)
{
int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
//使用三目操作符开辟空间大小
HPDataType* tmp = (HPDataType*)realloc(hp->a, newcapacity * sizeof(HPDataType));
if (tmp == NULL)
{
perror("realloc fail");
return;
}
hp->a = tmp;
hp->capacity = newcapacity;
}
hp->size++;
hp->a[hp->size] = x;
//向下调整法,因为每次的插入是在数组末尾
//每次插入需要与父亲比较大小交换
AdjustUp(hp->a, hp->size - 1);
}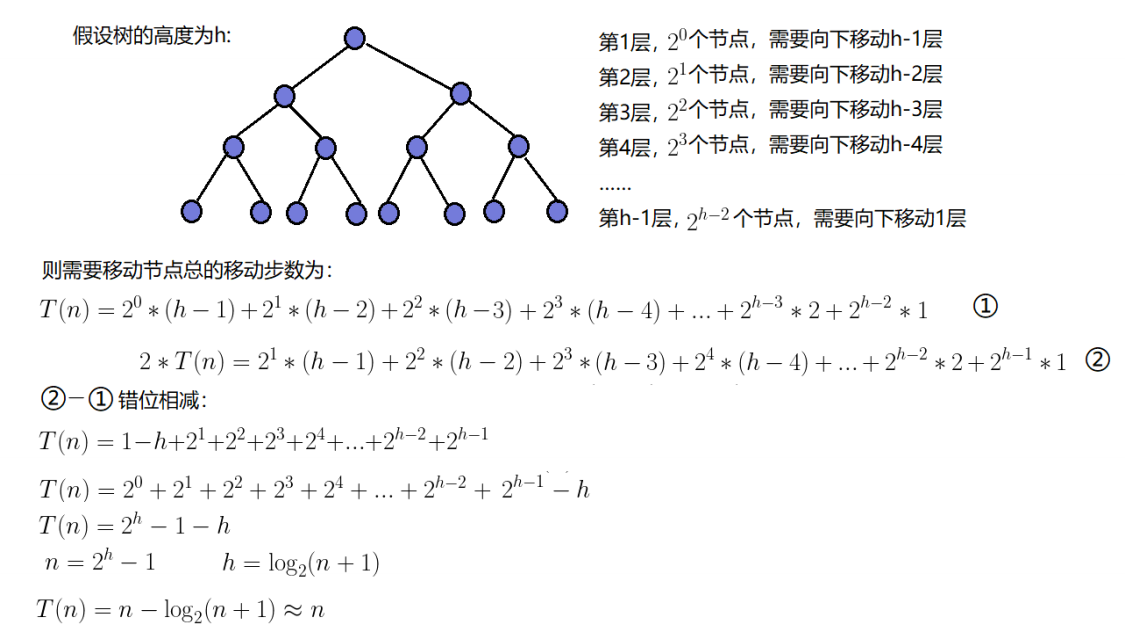
等比数列求和公式:
建堆要从倒数第一个非叶子节点开始调整,也即是从倒数第二层开始调,可得出时间复杂度公式:T ( n ) = ∑ ( 每 层 节 点 数 ∗ ( 堆 的 高 度 − 当 前 层 数 ) )
建堆的时间复杂度为O(N)。(向下调整算法)
为何使用向下调整建堆而不使用向上调整建堆
5.1.2向上调整法建堆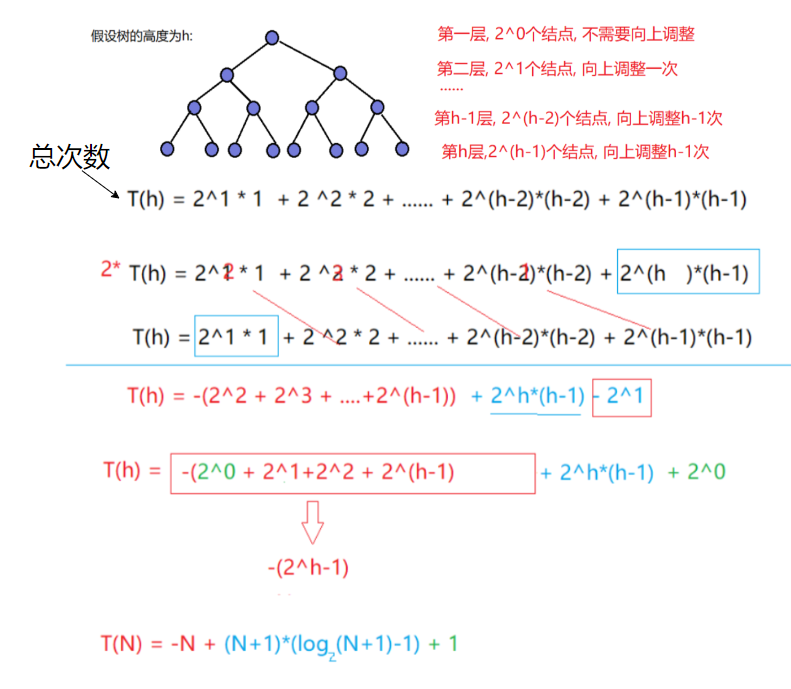
可以看出结点数多的层, 调整次数也多, 结点数少的层, 调整次数少, 时间复杂度为O(N*logN), 所以一般建堆都采用向下调整建堆法.
6、TOPK问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前十、世界500强、销量最高的前十、富豪榜等等
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能
数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1. 用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
2. 用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
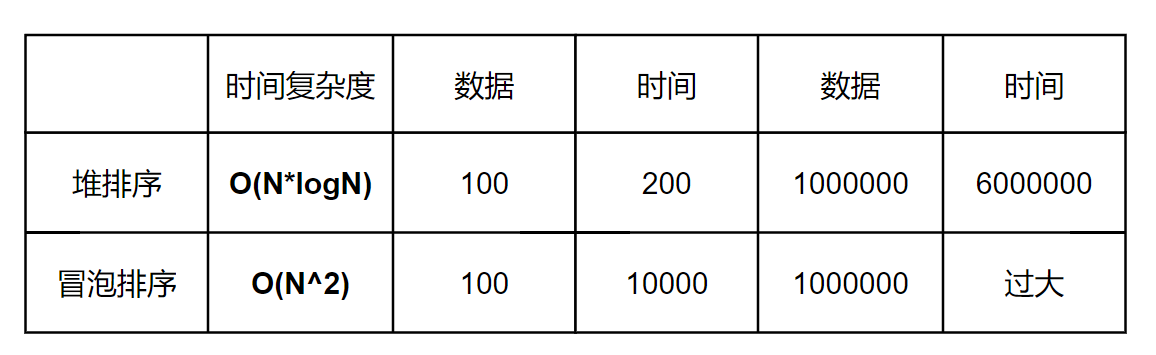
我们常常会想到冒泡排序( O(N^2) )
对于少量的数据是可以拿捏的,但面对100000的数据就显得有点吃力,而堆排序O(N*logN)则觉得轻而易举
7、堆排序
void HeapSort(int* a, int n)
{
// 降序,建小堆
// 升序,建大堆
// 向上调整建堆 O(N*logN)
/*for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}*/
// 向下调整建堆 O(N)
for (int i = (n-1-1)/2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
// O(N*logN)
int end = n - 1;
while (end > 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}哇呜!点个赞走吧!!!