基于python多模型并行的新闻分类

文章目录

研究目的及意义
解决思路
数据分析
- 数据集说明
特征选取
- TF-IDF
算法选取

研究目的及意义

随着互联网的高速发展，每天都会产生大量的数据。而新闻是人们获取信息，了解时事热点的重要途径。但是面对规模巨大且不断增长的文本信息，依靠人工海量的进行文本信息的分类是不切实际的。因此能够借助机器学习的手段正确的对新闻进行自动化分类是十分重要的，不仅可以帮助用户提高检索效率，提高用户的阅读体验，且能协助网站运营人员了解用户需求，让信息更有效的得到利用。

解决思路

本文首先用Dask进行数据集的导入，然后对数据集进行数据预处理，拆分开新闻标签，新闻标题内容。将新闻标签进行数值型的映射，以及将新闻标题文本数据向量化成特征，再选取模型进行多模型的训练。

本文选取的模型有Logistic、随机森林、决策树、XGBoost、SVM，分别根据其训练集时长以及测试集准确率综合考虑选取的、进行投票法的三个模型，最后再根据最终的准确率以及时长选出最佳模型。

数据分析

数据集说明

数据集为382688行，新闻标签与新闻内容未进行拆分。数据集展示如下：
在这里插入图片描述
标签量化映射关系如下表所示，共有15类。

特征选取

将文本数据转换为数值特征向量的过程称为文本向量化，由于文本是非结构化数据，在向量化过程中，需要将其转化为结构化数据。

TF-IDF

本文通过CountVectorizer 类，将文档向量化处理，计算方式如下:
$idf_{i}=log\frac{|D|}{|j:t_{i}\in d_j|}$
其中， $tf_{i,j}$ 为词频，指一个单词在文档中出现的次数。分子是该词在文件中的出现次数，而分母则是在文件中所有字词的出现次数之和。
$idf_{i}=log\frac{|D|}{|j:t_{i}\in d_j|}$
其中， $idf_{i}$ 为逆文档频率。分子为语料库中的文件总数，分母为包含词语的文件数目。TF-IDF计算公式如下：
$TF-IDF=tf_{i,j} \times idf_{i}$

算法选取

Logistic回归模型\是一种广义线性回归模型。Logistic 回归模型中响应变量为 $Y$ ，解释变量 $x_1$ , $x_2,\cdots,x_m$ 对 $Y$ 有影响，则 $x_1$ , $x_2,\cdots,x_m$ 给定的条件下的概率 $p=P(Y=1|x_1,x_2,\cdots,x_m)$ ，Logistic回归方程为：

$p=\frac{e^{\beta _0+\beta _1x_1+\cdots +\beta _mx_m}}{1+e^{\beta _0+\beta _1x_1+\cdots +\beta _mx_m}}$

其中为截距项，为回归系数，需要说明的是 $x_1$ ， $x_2$ …， $x_m$ 既可以是连续变量，也可以是分类变量，对上述模型坐 $l o g i t$ 变换，Logistic回归模型可以用一下形式表示：

$logit(p)=ln(\frac{p}{1-p} )=\beta_0+\beta_1x_1+\cdots +\beta_mx_m$

随机森林

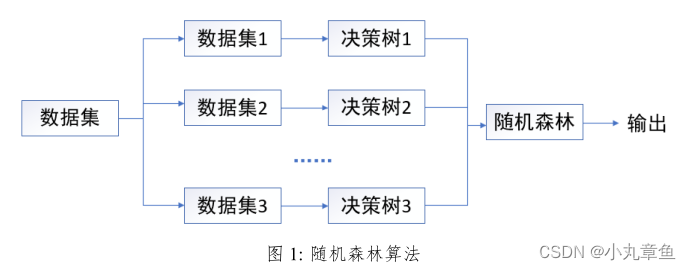
随机森林是一种集成学习算法，它将决策树作为基分类器，创建Bagging集成，并且将随机属性选择机制加入到决策树训练中。随机森林算法将自身的变量重要性度量用作对高维数据的特征选择工具既具有良好的鲁棒性又具备较高的学习效率，能使异常数据或缺失值数据得到很好地处理。

随机森林算法由Leo Breiman提出的，随机森林是个集成分类器，它由多个决策树分类器共同构成。分类器组合为 $\left \{h(X,\theta _t) ,k=1,2,\dots K \right \}$ ，其中0，是随机变量，服从于独立同分布，为随机森林中决策树的个数.在已知自变量入的情况下，最优的分类结果通过每个决策树分类器投票决定。

如下图所示，对数据集进行有放回地重复抽样得到K个子数据集，针对每个子数据集都有一个相应的决策树作为基学习器，最后这些决策树共同组成的分类器就是随机森林。随机森林算法结构图如下图所示。
在这里插入图片描述
在每个基学习器完成对样本的预测之后，需要将所有基学习器的预测结果进行输出最终的结果。

SVM

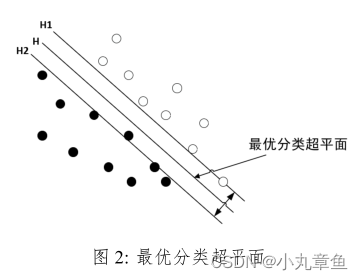
支持向量机是一种基于小样本统计理论的算法，主要用来进行分类。通过最大化超平面和数据之间的余量从而找到最优分类超平面。

设输入为 $x_i(i=1,2,\cdots,M)$ ，其中 $M$ 为样本数量。在线性数据的情况下可以确定能分离给定输入数据的超平面 $f (x) = 0$

$f(x)=w^Tx+b=0$
式中， $w$ 是 $M$ 维权重向量， $b$ 是偏置标量。 $w$ 和 $b$ 决定了超平面与原点之间的距离。通过求解下述最优化问题从而实现不同类之间的距离最大化，即:
$\max_{w,b}\frac{2b}{||w||^2}$
对于线性不可分问题,引入松驰变量 $\varepsilon_i\ge 0$ 和惩罚因子 $C$ , 从而过渡到软间隔支持向量机:
$\min_{w,b\varepsilon_i }\frac{1}{2} ||w||^2+C\sum_{i=1}^{n} \varepsilon_i$
支持向量机算法示意图：
在这里插入图片描述

决策树

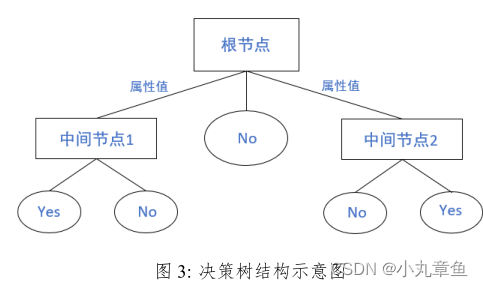
决策树是一个树结构（可以是二叉树或非二叉树）。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。使用决策树进行决策的过程就是从根节点开始，测试待分类项中相应的特征属性，并按照其值选择输出分支，直到到达叶子节点，将叶子节点存放的类别作为决策结果。下图为决策树结构示意图。
在这里插入图片描述

XGBoost

XGBoost是一种基于梯度提升算法以及决策树的改进型学习方法。其原理是运用了迭代运算的思想，将大量的弱分类器转化为强分类器，以实现准确的分类效果。XGBoost是Boosting中的经典方法。Boosting算法的宗旨是通过将许多弱分类器集成，构造一个强分类器，其中XGBoost使用的是CART回归树。

XGBoost是在Adaboost与GDBT等及集成提升算法的基础上进行优化的集成算法。其主要特点有两方面，一是将损失函数进行二次泰勒展开，同时加入正则项，使经验风险顺势函数与结构风险损失函数最小化，提升模型的泛化能力；二使加入近似分割点算法，提升运行效率。

多种算法运行结果

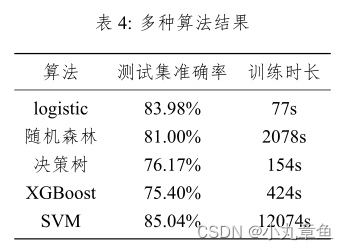
使用多种算法算得的测试集准确率如下：
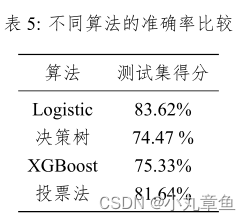
在这里插入图片描述

结合测试集得分以及训练集训练时长，本文采用对logistic，决策树，XGBoost 进行并行处理。

算法的并行处理

运用模型并行，对上述的三个算法进行并行运行，并对其进行投票。

核心代码如下：

def model1(score):
    #logostic
    log_model = LogisticRegression()
    log_model.fit(X_train_tran,y_train)
    score1=log_model.score(X_test_tran,y_test)
    print('logistic准确率：',score1)
    return score1

def model2(score):
    #决策树
    tree_model = DecisionTreeClassifier()
    tree_model.fit(X_train_tran,y_train)
    score2=tree_model.score(X_test_tran,y_test)
    print('决策树准确率：',score2)
    return score2

def model3(score):
    #XGBoost
    le = LabelEncoder()
    y_train1 = le.fit_transform(y_train)
    y_test1 = le.fit_transform(y_test)
    xgboost_model=XGBClassifier(n_estimators = 400, learning_rate = 0.1, max_depth = 3)
    xgboost_model.fit(X_train_tran,y_train1)
    score3=xgboost_model.score(X_test_tran,y_test1)
    print('XGBoost准确率：',score3)
    return score3

def voting():
    voting_clf = VotingClassifier(estimators=[('logistic',LogisticRegression() ),('dec_tree',DecisionTreeClassifier() ),('XGBoost',XGBClassifier() )],#estimators:子分类器
                              voting='hard')
    voting_clf.fit(X_train_tran,y_train)
    score4=voting_clf.score(X_test_tran,y_test)
    print('投票法准确率：',score4)


def model_Parallel():
    p1 = Thread(target = model1,args=(1,))
    p2 = Thread(target = model2,args=(2,))
    p3 = Thread(target = model3,args=(3,))
    p1.start()
    p2.start()
    p3.start()
    p1.join()
    p2.join()
    p3.join()

并行运行的时间为478s，得出各种算法的测试集准确率如下：
在这里插入图片描述