很多学it的都知道，浮点型会存在精度问题，但是，这个精度问题是怎么出现的？浮点型又是怎么存储在计算机里的，这些都会在本章进行揭秘，首先我们来看一张图

在计算机中，1字节是8位，float占4字节，因此float的数据长度用二进制表示就是32位，double占8字节，用二进制表示就是64位。

如图所示，浮点型不管是float还是doubule，在计算机中都由三部分组成

但是浮点数据，怎么转换成二进制，又如何存到内存里？这涉及到一系列的复杂运算，步骤如下

1.将这个实数的绝对值化为二进制格式
2.将这个二进制格式实数的小数点左移或右移N（指数）位，直到小数点移动到第一个有效数字的右边
3.从小数点右边第一位开始数出二十三位数字放入第22到第0位
4.如果实数是正的，则在第31位放入“0”，否则放入“1”
5.如果N是左移得到的，说明指数是正的，第30位放入“1”。如果N是右移得到的或n=0，则第30位放入“0”
6.如果N是左移得到的，则将n减去1后化为二进制，并在左边加“0”补足七位，放入第29到第23位。
  如果N是右移得到的或N=0，则将N化为二进制后在左边加“0”补足七位，再各位求反，再放入第29到第23位。

实操，将10.25转成二进制存储格式

一：将实数转为二进制

1.整数部分

需要除以2，除到结果等于0为止，每次除完的余数，逆着算，就是整数部分的二进制，如下图所示，结果为1010

因此10.25的整数部分二进制

2.小数部分

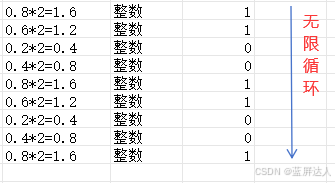
需要乘以2，直到没有小数为止，每次乘完后的整数部分，正着算，就是小数部分的二进制，如下图所示，结果为01

因此10.25的二进制表示为1010.01

但是，小数部分如果是0.8怎么办呢？

如上图所示，小数部分一直不会变成0，这种情况的出现，就是精度丢失的问题所在！所以才会有保留几位小数的出现。

二：将这个二进制格式实数的小数点左移或右移N（指数）位，直到小数点移动到第一个有效数字的右边

二进制的有效数，意思就是1，这一步操作，需要将一个二进制形式的小数，变成1.xxx的样子

比如我们拆的二进制数1010.01

需要变成1.01001，1010.01 = 1.01001 * 2³，这个指数3，就是我们要得到的N

三：从小数点右边第一位开始数出二十三位数字放入第22到第0位

小数点后面的数字是01001，填充到22~0位，也就是23个数字，少的以0补全，最后得到的数字如下图进行填充

四：如果实数是正的，则在第31位放入“0”，否则放入“1”

这个简单，我们的是正数，因此如下图

五：如果N是左移得到的，说明指数是正的，第30位放入“1”。如果N是右移得到的或n=0，则第30位放入“0”

因为我们的指数，是小数点左移得到的，因此放入1

6.如果N是左移得到的，则将N减去1后化为二进制，并在左边加“0”补足七位，放入第29到第23位。如果N是右移得到的或N=0，则将N化为二进制后在左边加“0”补足七位，再各位求反，再放入第29到第23位。

我们的3是小数点左移得到的，因此3-1=2，2的二进制是10，补足至7位，则变成了0000010

最后得到的32个数字，就是内存中存储的样子

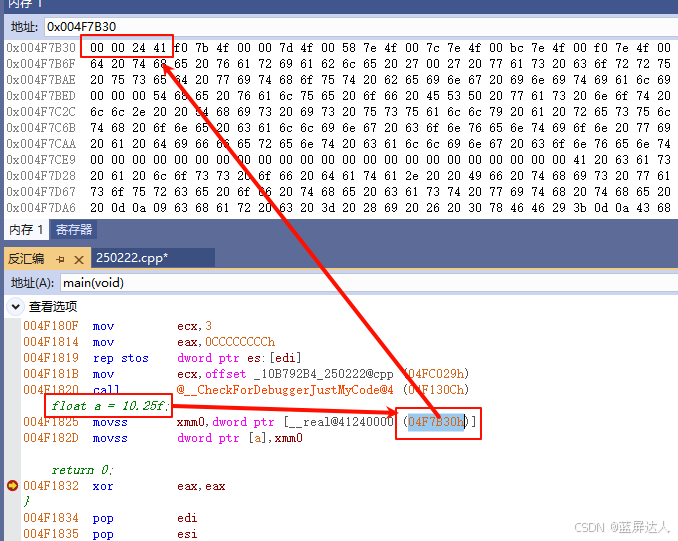
二进制：0100 0001 0010 0100 0000 0000 0000 0000

十六进制：4124 0000

我们在代码里验证一下，如下图所示，与我们计算的是一样的（内存中的数据是小端序显示）