一、前言

好久没打蓝桥杯官网上的比赛了，回来感受一下，这难度区分度还是挺大的

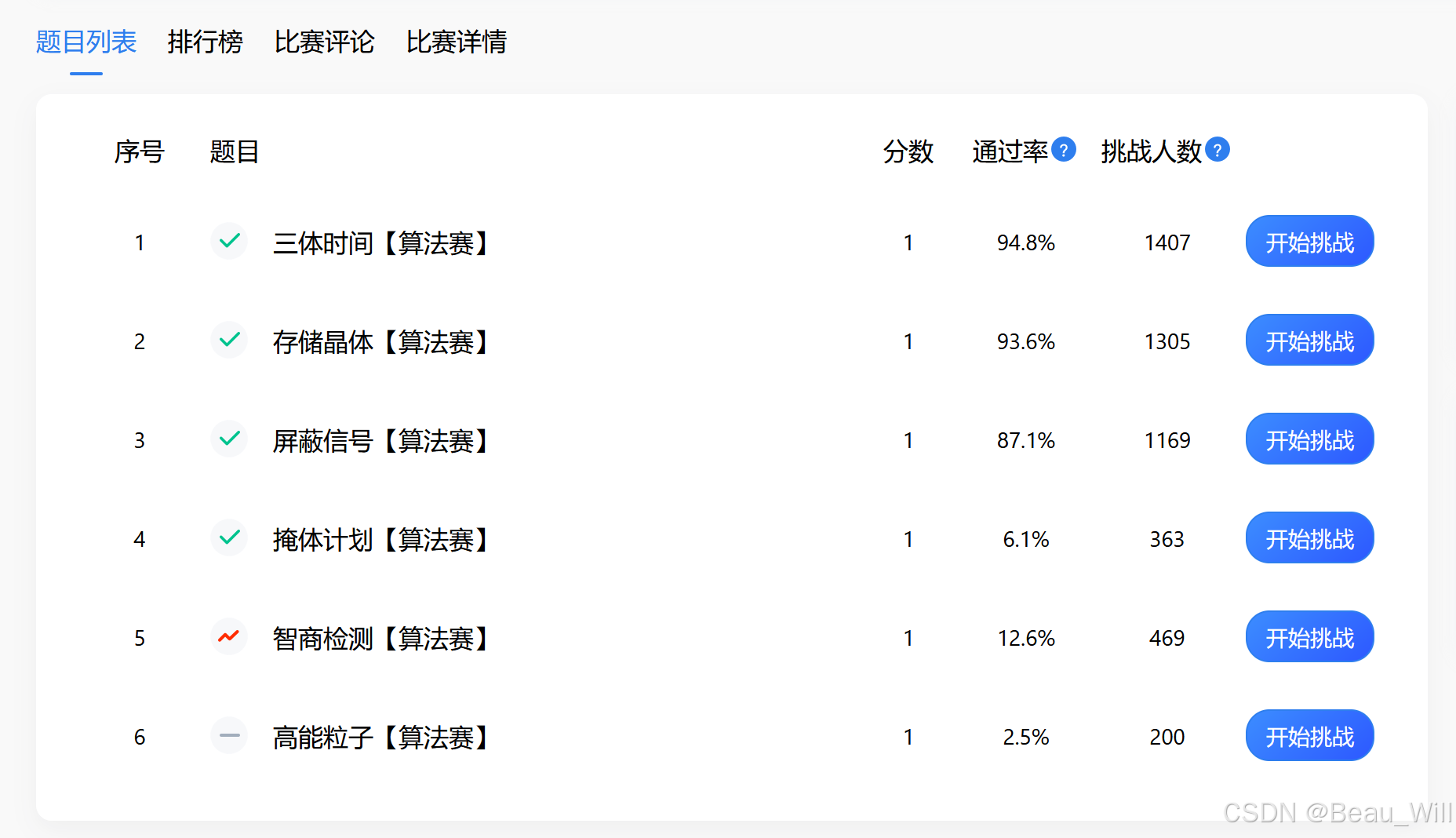
二、题目总览

三、具体题目

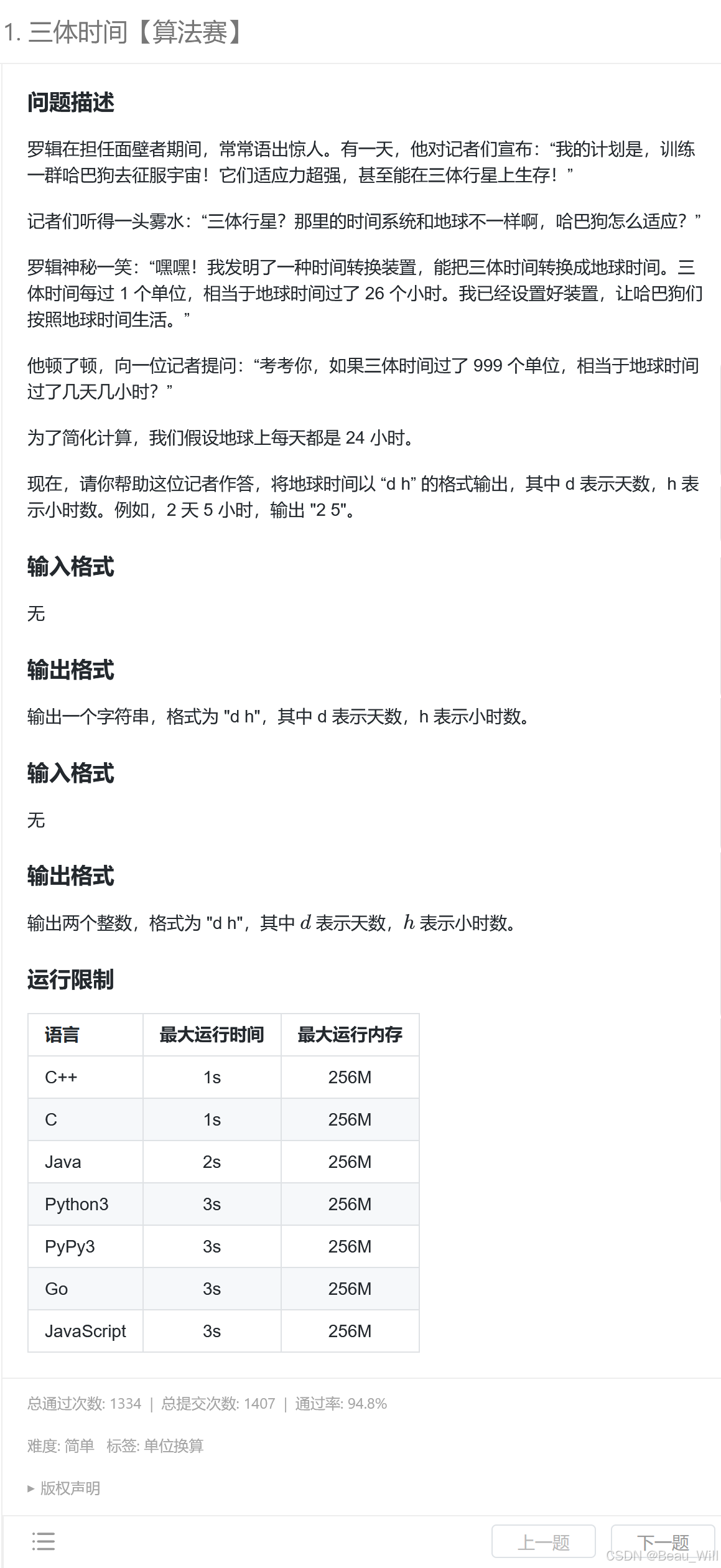
3.1 1. 三体时间【算法赛】

思路

额...签到题

我的代码

// Problem: 1. 三体时间【算法赛】
// Contest: Lanqiao - 第 23 场 小白入门赛
// URL: https://www.lanqiao.cn/problems/20058/learning/?contest_id=224
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using pii = std::pair<int,int>;
constexpr int N = 1e5+5,M = 1e6+5,INF = 0x3f3f3f3f;
#define pb emplace_back
#define all(v) v.begin(),v.end()

void solve(){
	std::cout << 999*26/24 << ' ' << 999*26%24 << '\n';
}

int main(){
	std::cin.tie(nullptr)->sync_with_stdio(false);
	
	int tt = 1;
	// std::cin >> tt;
	for(int ti = 0;ti<tt;++ti){
		solve();
	}
	
	return 0;
}

3.2 2. 存储晶体【算法赛】

思路

直接平方判断大小就行了

我的代码

// Problem: 2. 存储晶体【算法赛】
// Contest: Lanqiao - 第 23 场 小白入门赛
// URL: https://www.lanqiao.cn/problems/20056/learning/?contest_id=224
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using pii = std::pair<int,int>;
constexpr int N = 1e5+5,M = 1e6+5,INF = 0x3f3f3f3f;
#define pb emplace_back
#define all(v) v.begin(),v.end()

void solve(){
    int a,b;std::cin >> a >> b;
    int n;std::cin >> n;
    while(n--){
        int c;std::cin >> c;
        std::cout << (c*c<=a*a+b*b?"YES\n":"NO\n");
    }
}

int main(){
    std::cin.tie(nullptr)->sync_with_stdio(false);
    
    int tt = 1;
    // std::cin >> tt;
    for(int ti = 0;ti<tt;++ti){
        solve();
    }
    
    return 0;
}

3.3 3. 屏蔽信号【算法赛】

思路

简单的类gcd的模拟题

我的代码

// Problem: 3. 屏蔽信号【算法赛】
// Contest: Lanqiao - 第 23 场 小白入门赛
// URL: https://www.lanqiao.cn/problems/20057/learning/?contest_id=224
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using pii = std::pair<int,int>;
constexpr int N = 1e5+5,M = 1e6+5,INF = 0x3f3f3f3f;
#define pb emplace_back
#define all(v) v.begin(),v.end()


void solve(){
    i64 a,b;std::cin >> a >> b;
    if(a<b) std::swap(a,b);
    int cnt = 0;
    while(b){
        i64 tmp = a-b;
        a = tmp;
        if(a<b) std::swap(a,b);
        ++cnt;
    }
    std::cout << cnt << '\n';
}

int main(){
    std::cin.tie(nullptr)->sync_with_stdio(false);
    
    int tt = 1;
    std::cin >> tt;
    for(int ti = 0;ti<tt;++ti){
        solve();
    }
    
    return 0;
}

3.4 4. 掩体计划【算法赛】

思路

题目要求是找到分支次数最小的叶子结点（起爆装置）的分支次数

我的代码

// Problem: 4. 掩体计划【算法赛】
// Contest: Lanqiao
// URL: https://www.lanqiao.cn/problems/20053/learning/?contest_id=224
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include<bits/stdc++.h>
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;
using pii = std::pair<int,int>;
constexpr int N = 1e5+5,M = 1e6+5,INF = 0x3f3f3f3f;
#define pb emplace_back
#define all(v) v.begin(),v.end()

int n,m;
std::vector<std::vector<int>> edges(N);
std::vector<int> f(N);
std::vector<int> bomb;

void bfs(){
    std::queue<int> q;
    q.emplace(1);
    while(!q.empty()){
        auto t = q.front();
        q.pop();
        if(edges[t].size()>1){
            ++f[t];
        }
        for(const auto&to:edges[t]){
            if(!f[to]){
                f[to] = f[t];
                q.emplace(to);
            }
        }
    }
}

void solve(){
    std::cin >> n;
    for(int i = 0;i<n-1;++i){
        int u,v;std::cin >> u >> v;
        edges[u].pb(v);
        // edges[v].pb(u);
    }
    std::cin >> m;
    while(m--){
        int t;std::cin >> t;
        bomb.pb(t);
    }
    bfs();
    int ans = INF;
    for(const auto &b:bomb){
        ans = std::min(ans,f[b]);
    }
    std::cout << ans << '\n';
}

int main(){
    std::cin.tie(nullptr)->sync_with_stdio(false);
    
    int tt = 1;
    // std::cin >> tt;
    for(int ti = 0;ti<tt;++ti){
        solve();
    }
    
    return 0;
}

3.5 5. 智商检测【算法赛】

思路

线性dp，dp[i][j] 保存的是从前i个元素中删除j个元素得到的最大 gcd值，状态转移主要是考虑是否删除第i个元素，另外要注意的是i和j也存在限制关系

题解代码

// Problem: 5. 智商检测【算法赛】
// Contest: Lanqiao - 第 23 场 小白入门赛
// URL: https://www.lanqiao.cn/problems/20055/learning/?contest_id=224
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <bits/stdc++.h>
constexpr int N = 1e5 + 10;
int n, k;
int a[N];
#define gcd std::__gcd
int main(){
	std::cin.tie(nullptr)->sync_with_stdio(false);
    std::cin >> n >> k;
    for(int i = 1;i<=n;++i){
        std::cin >> a[i];
    }
    std::vector<std::vector<int>> dp(n+1,std::vector<int>(k+1,0));
    // dp[i][j] 从前i个元素中删除j个元素, 得到的最大 gcd
    for(int i = 1;i<=n;++i){
        dp[i][0] = gcd(dp[i-1][0],a[i]); // 初始化
    }
    for(int i = 1;i<=n;++i){
        for(int j = 1; j<=std::min(i,k);++j){
            if(i-1>=j) dp[i][j] = gcd(dp[i-1][j],a[i]);//可以不删, 即选择 a[i]
            dp[i][j] = std::max(dp[i-1][j-1],dp[i][j]);//删去 a[i], 并从前i-1个中选择删除j-1个元素
        }
    }
    std::cout << dp[n][k] << '\n';
    return 0;
}

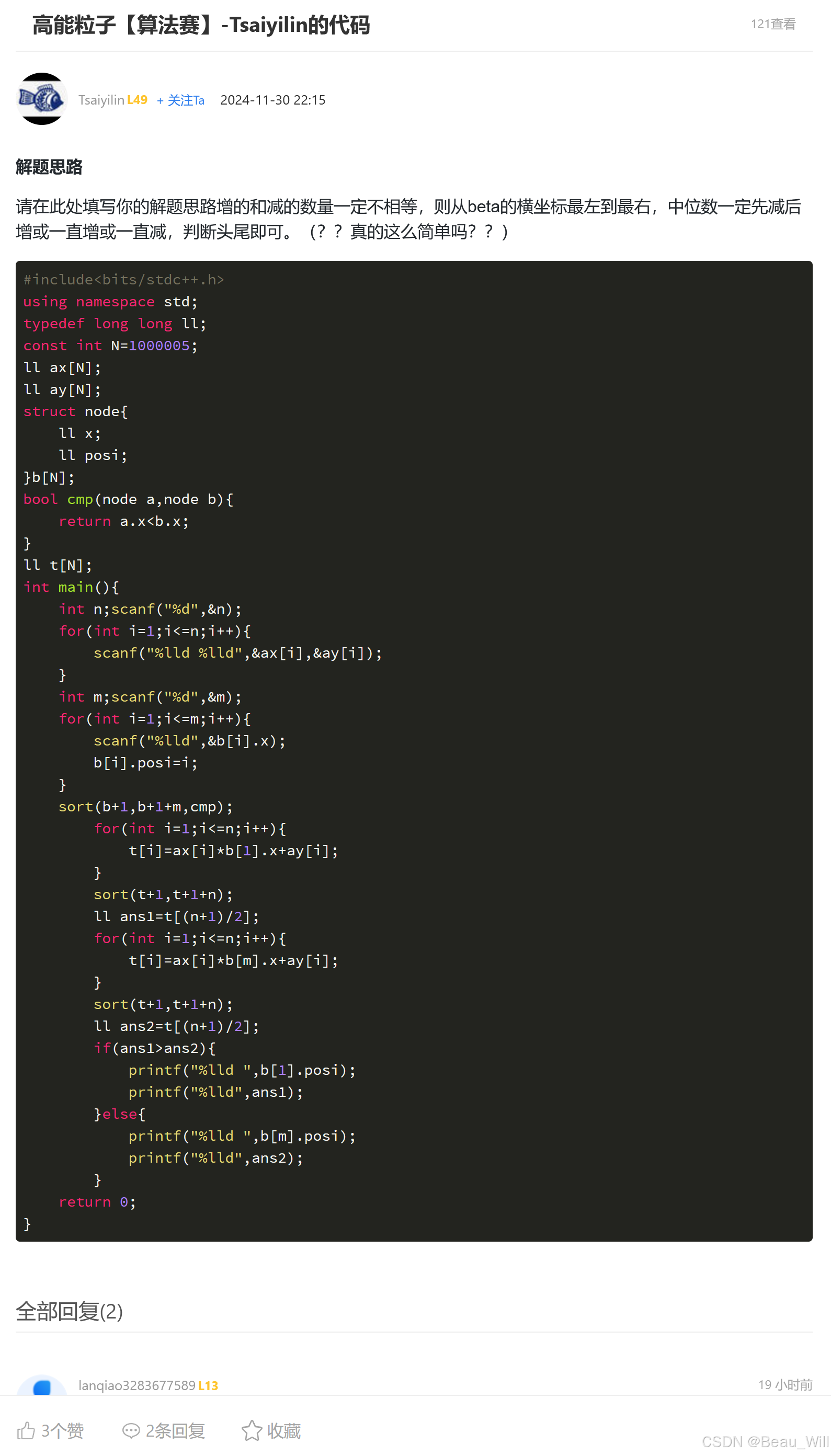
3.6 6. 高能粒子【算法赛】

思路

看看大佬的思路

题解代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1000005;
ll ax[N];
ll ay[N];
struct node{
    ll x;
    ll posi;
}b[N];
bool cmp(node a,node b){
    return a.x<b.x;
}
ll t[N];
int main(){
    int n;scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld %lld",&ax[i],&ay[i]);    
    }
    int m;scanf("%d",&m);
    for(int i=1;i<=m;i++){
        scanf("%lld",&b[i].x);
        b[i].posi=i;
    }
    sort(b+1,b+1+m,cmp);
        for(int i=1;i<=n;i++){
            t[i]=ax[i]*b[1].x+ay[i];
        }
        sort(t+1,t+1+n);
        ll ans1=t[(n+1)/2];
        for(int i=1;i<=n;i++){
            t[i]=ax[i]*b[m].x+ay[i];
        }
        sort(t+1,t+1+n);
        ll ans2=t[(n+1)/2];
        if(ans1>ans2){
            printf("%lld ",b[1].posi);
            printf("%lld",ans1);
        }else{
            printf("%lld ",b[m].posi);
            printf("%lld",ans2);
        }
    return 0;
}