Base64 - 悦读

什么是Base64

base64是一种使用64个可见字符来表示二进制数据的方法。因为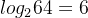 $log_{2} {64}=6$ ，以6位为一个单元，表示为一个可见字符。二进制数据每3个字节为一组，共24位，用4个可见字符表示。‘A’-‘Z’，‘a’-‘z’，‘0’-‘9’一共62个字符，剩下2个字符在不同系统中表示不一样。

base64对照表

十进制	二进制	字符	十进制	二进制	字符	十进制	二进制	字符	十进制	二进制	字符
0	000000	A	16	010000	Q	32	100000	g	48	110000	w
1	000001	B	17	010001	R	33	100001	h	49	110001	x
2	000010	C	18	010010	S	34	100010	i	50	110010	y
3	000011	D	19	010011	T	35	100011	j	51	110011	z
4	000100	E	20	010100	U	36	100100	k	52	110100	0
5	000101	F	21	010101	V	37	100101	l	53	110101	1
6	000110	G	22	010110	W	38	100110	m	54	110110	2
7	000111	H	23	010111	X	39	100111	n	55	110111	3
8	001000	I	24	011000	Y	40	101000	o	56	111000	4
9	001001	J	25	011001	Z	41	101001	p	57	111001	5
10	001010	K	26	011010	a	42	101010	q	58	111010	6
11	001011	L	27	011011	b	43	101011	r	59	111011	7
12	001100	M	28	011100	c	44	101100	s	60	111100	8
13	001101	N	29	011101	d	45	101101	t	61	111101	9
14	001110	O	30	011110	e	46	101110	u	62	111110	+
15	001111	P	31	011111	f	47	101111	v	63	111111	/

示例说明

以字符串"abc"为例:

二进制表示为 01100001 01100010 01100011

6个字节为一组011000 010110 001001 100011 ,一共4组

将分组后的二进制转换为十进制,在对照表中找到对应的字符,即可得到编码结果YWJj.

文本	a								b								c
ASCII	97								98								99
二进制	0	1	1	0	0	0	0	1	0	1	1	0	0	0	1	0	0	1	1	0	0	0	1	1
索引	24						22						9						35
Base64	Y						W						J						j

如果出现要编码的字节数不能被3整除,多出来1个或者2个字节,这时候就需要额外处理.

先用"0"在二进制形式下补足,然后进行base64编码,最后在编码结果后添加1个或者2个"=",以表示补充的字节数.

多2个字节的情况,以字符串"ab"为例

补足0之后编码结果为YWI,因为差一个字节被3整除,因此添加1个"=",最终的编码结果就为YWI=

文本	a								b
ASCII	97								98
二进制	0	1	1	0	0	0	0	1	0	1	1	0	0	0	1	0	0	0	0	0	0	0	0	0
索引	24						22						8
Base64	Y						W						I						=

多1个字节的情况,以字符串"a"为例:

补足0之后编码结果为YQ,因为差2个字节被3整除,因此添加2个"=",最终的编码结果就为YQ==

文本	a
ASCII	97
二进制	0	1	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
索引	24						16
Base64	Y						Q						=						=

代码实现

编码

  private static final char[] TABLE = {
      'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M',
      'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z',
      'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm',
      'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z',
      '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', '/'
  };

  public static byte[] encode(byte[] src) {
    int length = (src.length + 2) / 3 * 4;
    byte[] dst = new byte[length];
    int size = src.length / 3;
    int dpos = 0, spos = 0;
    for (int i = 0; i < size; i++) {
      //3个字节为一组，共24个字节，用4个字符表示
      int bit = src[spos++] << 16 | src[spos++] << 8 | src[spos++];
      dst[dpos++] = (byte) TABLE[(bit >>> 18)];
      dst[dpos++] = (byte) TABLE[((bit & 0x3ffff) >>> 12)];
      dst[dpos++] = (byte) TABLE[((bit & 0xfff) >>> 6)];
      dst[dpos++] = (byte) TABLE[(bit & 0x3f)];
    }

    //最后一组不足3个字节，补充=
    if (spos != src.length) {
      int bit0 = src[spos++];
      dst[dpos++] = (byte) TABLE[bit0 >> 2];
      if (spos == src.length) {
        dst[dpos++] = (byte) TABLE[(bit0 << 4) & 0x3f];
        dst[dpos++] = '=';
      } else {
        int bit1 = src[spos++];
        dst[dpos++] = (byte) TABLE[((bit0 & 0x03) << 4) | bit1 >> 4];
        dst[dpos++] = (byte) TABLE[(bit1 & 0x0f) << 2];
      }
      dst[dpos++] = '=';
    }

    return dst;
  }

解码

  private static final int[] POS_TABLE = new int[256];

  static {
    for (int i = 0; i < TABLE.length; i++) {
      POS_TABLE[TABLE[i]] = i;
    }
  }

  public static byte[] decode(byte[] src) {
    int endCharCnt = (src[src.length - 1] == '=' ? 1 : 0)
        + (src[src.length - 2] == '=' ? 1 : 0);
    int len = src.length / 4 * 3 - endCharCnt;
    byte[] dst = new byte[len];
    int dpos = 0, spos = 0;
    int size = src.length / 4 - endCharCnt > 0 ? 1 : 0;
    for (int i = 0; i < size; i++) {
      //4个可见字符转换为3个字节
      int bit = (POS_TABLE[src[spos++]] << 18) |
          (POS_TABLE[src[spos++]] << 12)
          | POS_TABLE[src[spos++]] << 6
          | POS_TABLE[src[spos++]];
      dst[dpos++] = (byte) (bit >>> 16);
      dst[dpos++] = (byte) (bit >>> 8 & 0xff);
      dst[dpos++] = (byte) (bit & 0xff);
    }

    //处理=
    if (spos != src.length) {
      int bit = (POS_TABLE[src[spos++]] << 18)
          | (POS_TABLE[src[spos++]] << 12)
          | POS_TABLE[src[spos++]] << 6
          | POS_TABLE[src[spos++]];
      dst[dpos++] = (byte) (bit >>> 16);
      if (src[src.length - 2] != '=') {
        dst[dpos++] = (byte) (bit >>> 8 & 0xff);
      }
    }

    return dst;
  }