本篇文章主要介绍线性表中的折半查找与分块查找算法。

线性表的查找：

        1，查找的基本概念及顺序查找

        2，折半查找

折半查找：每次将待查记录所在区间缩小一半。（有序表表示静态查找表）

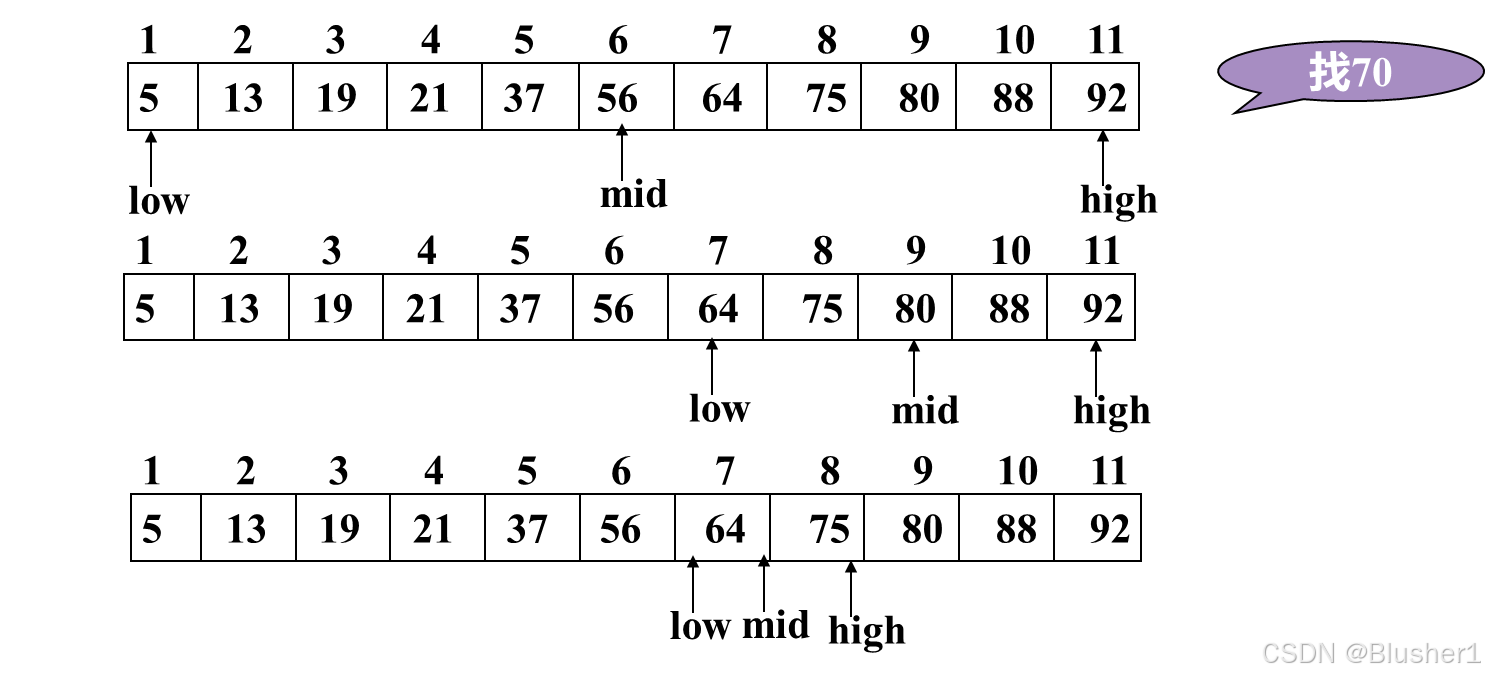
下面给出一个例子分析折半查找的过程，一共用到了两个指针high和low，mid始终等于（high+low）/2。

若k==R[mid].key，查找成功；若k<R[mid].key，则high=mid-1；若k>R[mid].key，则low=mid+1

若k==R[mid].key，查找成功

若k<R[mid].key，则high=mid-1

若k>R[mid].key，则low=mid+1

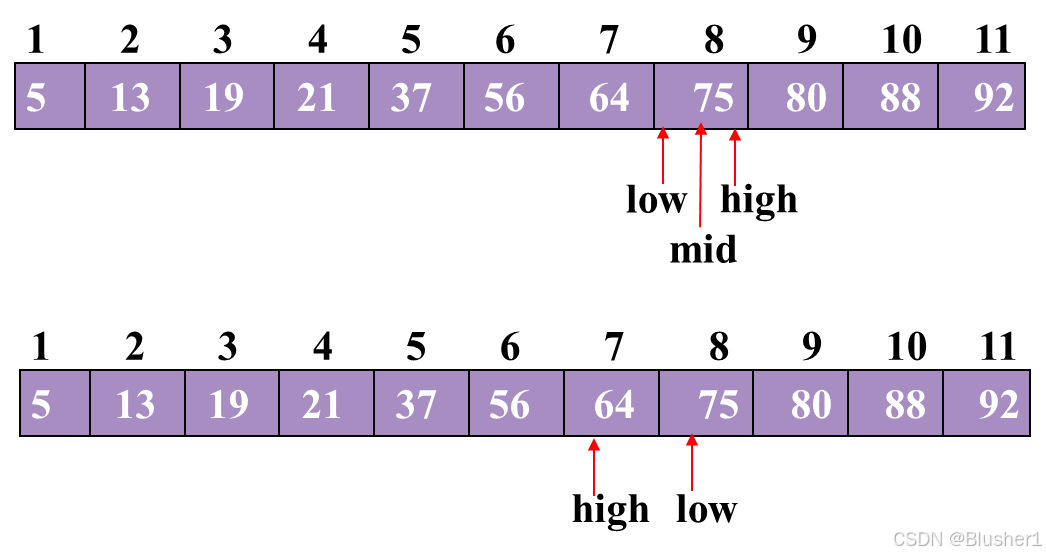
直至low>high时，查找失败

 由上述实例我们可以总结出折半查找的步骤：

以下是代码实例 

int Search_Bin(SSTable ST,KeyType key)
{
	//若找到，则函数值为该元素在表中的位置，否则为0
    low=1;high=ST.length;						 while(low<=high){
        mid=(low+high)/2;
        if(key==ST.R[mid].key) return mid; 
        else if(key<ST.R[mid].key) high=mid-1;    //前一子表查找
        else low=mid+1;                       		    //后一子表查找
    }									    return 0;		//表中不存在待查元素
}		

下面是使用递归算法

int Search_Bin (SSTable ST, keyType key, int low, int high) 
{ 
  if(low>high) return 0;   //查找不到时返回0 
  mid=(low+high)/2; 
  if(key等于ST.elem[mid].key)  return mid; 
  else if(key小于ST.elem[mid].key)  
    ……..//递归
  else…….  //递归
} 

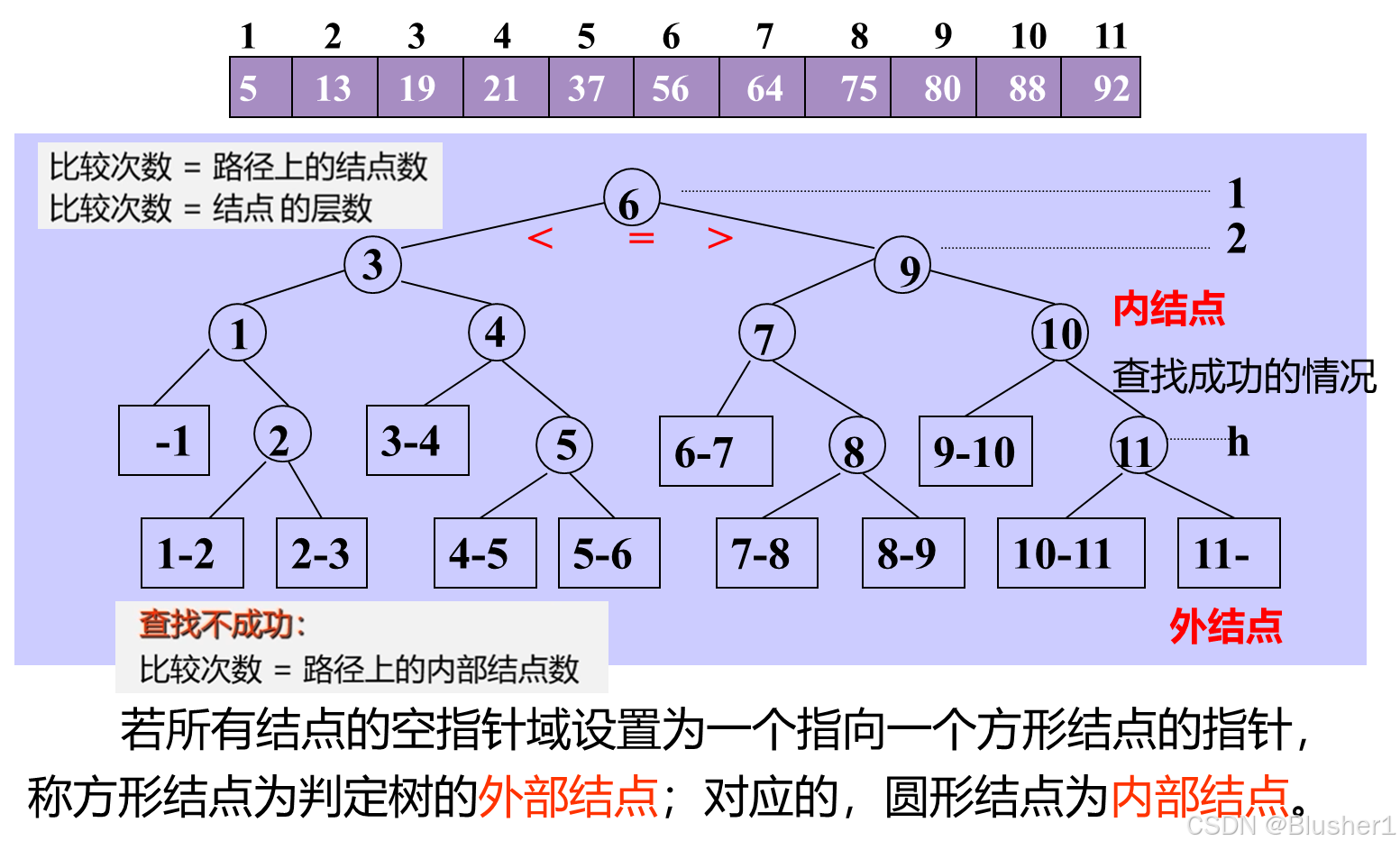
实际上我们可以使用二叉判定树来理解折半查找的过程

  比较的次数<=树的深度

下面是一个练习

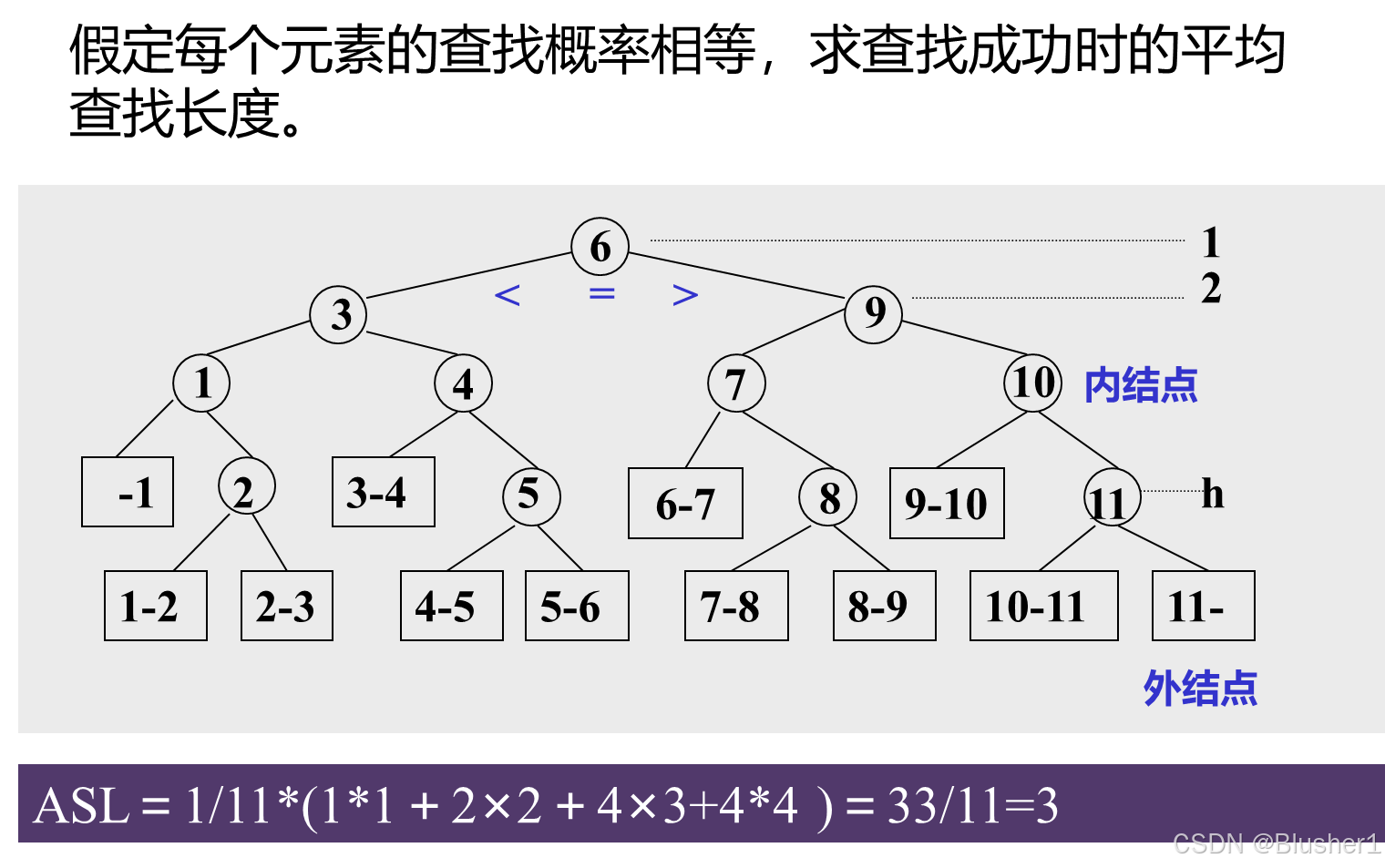
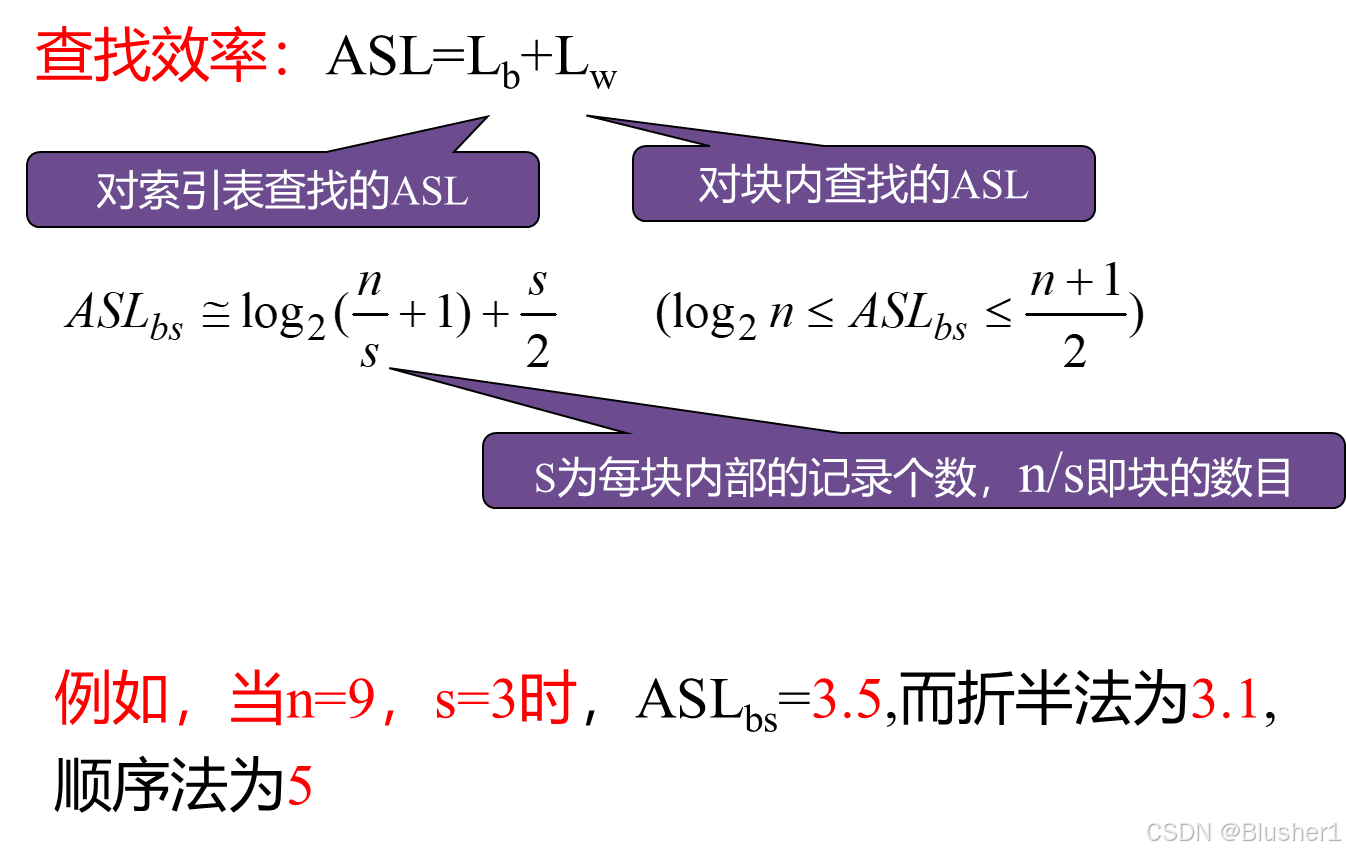
折半查找的性能分析：

 我们可以总结出折半查找的特点：

        3，分块查找 

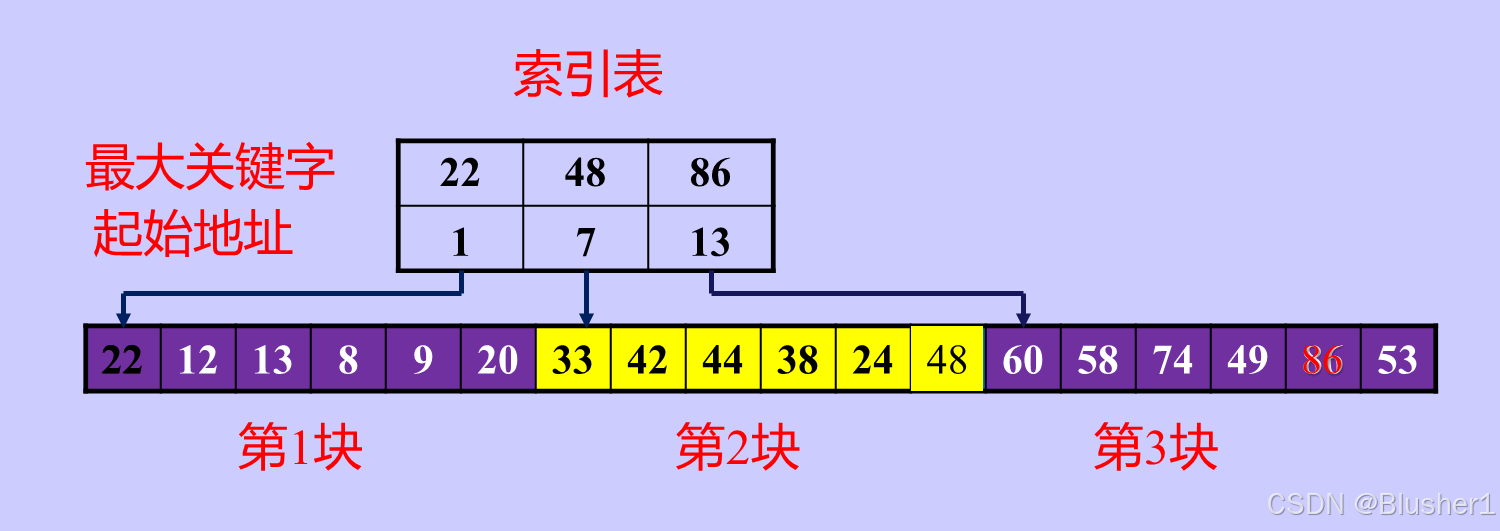
分块查找的特点是分块有序，块内无序。分块有序，即分成若干子表，要求每个子表中的数值都比后一块中数值小（但子表内部未必有序）。然后将各子表中的最大关键字构成一个索引表，表中还要包含每个子表的起始地址（即头指针）。我们通过下面这个图来理解。

 分块查找的过程：

① 对索引表使用折半查找法（因为索引表是有序表）；

② 确定了待查关键字所在的子表后，在子表内采用顺序查找法（因为各子表内部是无序表）；

 分块查找的优缺点：

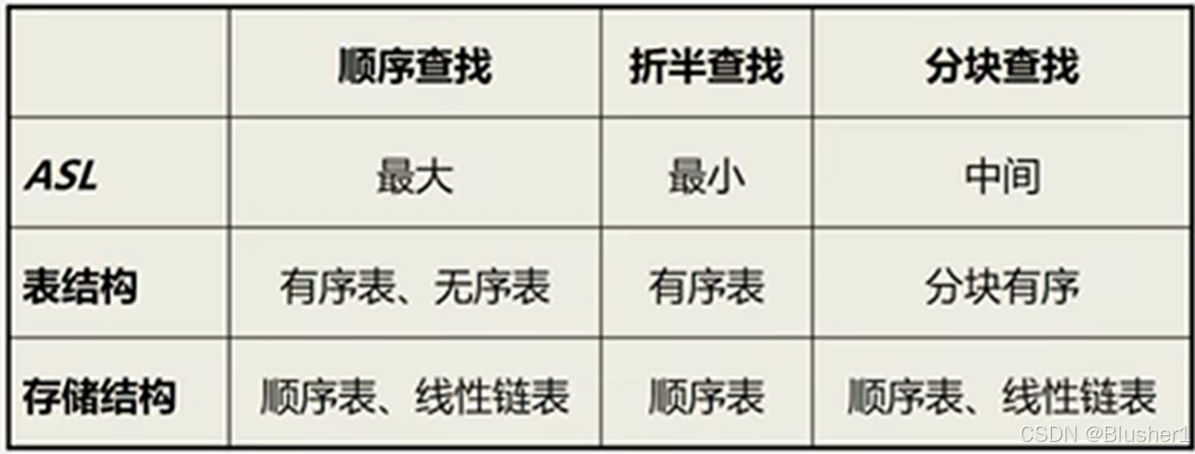
 4，线性表三种查找方法的比较：

折半折半查找的性能分析查找的性能分析 

直至直至low>high时，查找

直至low>high时，查找失败 

 直至low>high时，查找失败

直至low>high时，查找失败 

直至low>high时，查找失