3. 斜率优化

斜率优化是一个非常神奇的一种优化DP的方法，一般情况下，当我们的状态转移方程式中出现了形如 $xy$ 的式子，那这道题多半就是一道斜率优化

本篇帖子将浅谈一下斜率优化，顺便写篇水题的题解

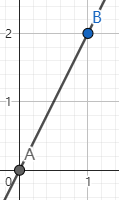
3.1. 前置知识：斜率

设直线AB的解析式为 $y=kx+b$，则 $k$ 为直线AB的斜率

怎么在不知道AB解析式的情况下求解该直线的斜率呢？

设 $A(x_a,y_a),B(x_b,y_b)$，则直线AB的斜率为 $\frac{y_a-y_b}{x_a-x_b}$

记住这个公式

3.2. 斜率优化介绍

在了解了斜率是什么后，我们就以一道例题作为小白鼠样例来讲解一下斜率优化

Eg [ZJOI2007] 仓库建设

3.2.1. 朴素DP

定义状态：

设dp[i]为在第 $i$ 号工厂必须建立仓库的费用，则易得状态转移方程式为：

d p [   i   ] = min ⁡ { d p [   j   ] + ∑ k = j + 1 i − 1 ( p [   k   ] × ( x [   i   ] − x [   k   ] ) ) } + c [   i   ] ( 0 ≤ j < i , 下同 ) = min ⁡ { d p [   j   ] + ∑ k = j + 1 i − 1 ( p [   k   ] × x [   i   ] − p [   k   ] × x [   k   ] ) } + c [   i   ] = min ⁡ { d p [   j   ] + x [   i   ] × ∑ k = j + 1 i − 1 ( p [   k   ] ) − ∑ k = j + 1 i − 1 ( p [   k   ] × x [   k   ] ) } + c [   i   ] \begin{aligned}dp[\ i\ ]&=\min\{dp[\ j\ ]+\sum\limits_{k=j+1}^{i-1}(p[\ k\ ]\times(x[\ i\ ]-x[\ k\ ]))\}+c[\ i\ ](0\le j<i,\text{下同})\\&=\min\{dp[\ j\ ]+\sum\limits_{k=j+1}^{i-1}(p[\ k\ ]\times x[\ i\ ]-p[\ k\ ]\times x[\ k\ ])\}+c[\ i\ ]\\&=\min\{dp[\ j\ ]+x[\ i\ ]\times\sum\limits_{k=j+1}^{i-1}(p[\ k\ ])-\sum\limits_{k=j+1}^{i-1}(p[\ k\ ]\times x[\ k\ ])\}+c[\ i\ ]\end{aligned} dp[ i ]​=min{dp[ j ]+k=j+1∑i−1​(p[ k ]×(x[ i ]−x[ k ]))}+c[ i ](0≤j<i,下同)=min{dp[ j ]+k=j+1∑i−1​(p[ k ]×x[ i ]−p[ k ]×x[ k ])}+c[ i ]=min{dp[ j ]+x[ i ]×k=j+1∑i−1​(p[ k ])−k=j+1∑i−1​(p[ k ]×x[ k ])}+c[ i ]​

设 $sump[i]=\sum _{k=1}^{i}p[i],sum[i]=\sum _{k=1}^i(p[i]\times x[i])$，则可以进一步化简状态转移方程式：

d p [   i   ] = min ⁡ { d p [   j   ] + x [   i   ] × ( s u m p [   i − 1   ] − s u m p [   j   ] ) − ( s u m [   i − 1   ] − s u m [   j   ] ) } + c [   j   ] dp[\ i\ ]=\min\{dp[\ j\ ]+x[\ i\ ]\times(sump[\ i-1\ ]-sump[\ j\ ])-(sum[\ i-1\ ]-sum[\ j\ ])\}+c[\ j\ ] dp[ i ]=min{dp[ j ]+x[ i ]×(sump[ i−1 ]−sump[ j ])−(sum[ i−1 ]−sum[ j ])}+c[ j ]

在我们没有学习斜率优化之前，我们只能将此方程式简化到这种程度，时间复杂度为 $O(n^2)$

现在，正式介绍一下斜率优化

3.2.2. 斜率优化优化DP

我们设有两个可选择的决策点 $j,k(k<j<i)$，并假设 $j$ 决策点优于 $k$ 决策点

根据上面的状态转移方程式，可以得到下述式子：

$$dp[j]+x[i]\times (sump[i-1]-sump[j])-(sum[i-1]-sum[j])+c[i]<dp[k]+x[i]\times (sump[i-1]-sump[k])-(sum[i-1]-sum[k])+c[i]$$

很长，是不是？

接下来，我们对这个式子进行化简：

$$\begin{array}{rl}dp[j]+x[i]\times (sump[i-1]-sump[j])-(sum[i-1]-sum[j])+c[i]& <dp[k]+x[i]\times (sump[i-1]-sump[k])-(sum[i-1]-sum[k])+c[i]\\ dp[j]-x[i]\times sump[j]+sum[j]& <dp[k]-x[i]\times sump[k]+sum[k]\\ dp[j]+sum[j]-(dp[k]+sum[k])& <x[i]\times (sump[j]-sum[k])\end{array}$$

因为 $k<j$，所以 $sump[k]<sump[j]$，因此该式子最终化简为：

$$\frac{dp[j]+sum[j]-(dp[k]+sum[k])}{sump[j]-sump[k]}<x[i]$$

同理，若 $j$ 决策点劣于 $k$ 决策点，最终会得到下述式子：

$$\frac{dp[j]+sum[j]-(dp[k]+sum[k])}{sump[j]-sump[k]}>x[i]$$

仔细看看左边的式子，是不是很眼熟？

联想一下斜率公式：$\frac{y_a-y_b}{x_a-x_b}$

是的，左边的式子其实就是在表示斜率

为了方便表示，我们把左边的式子表示为 $[j,k]$

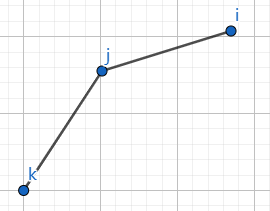
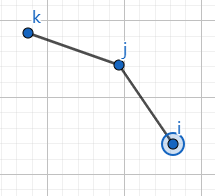
结合上面的两个式子，得出结论1：

若 $[j,k]<x[i]$，则说明 $j$ 决策点比 $k$ 决策点更优，若 $[j,k]>x[i]$，则说明 $k$ 决策点比 $j$ 决策点更优

这里，我们还要在推理一个结论2：

3.2.2.1.推理一个结论

先上结论

设有三个决策点 $i,j,k(k<j<i)$，若 $[i,j]<[j,k]$（即 $i,j$ 所表示的斜率小于了 $j,k$ 所表示的斜率），则 $j$ 决策点一定不是最优决策点

换言之，如果出现了这种情况：

或者这种情况：

那么，$j$ 决策点一定不是最优决策点

证明是显然的：

设当前所处理的点为 $P$

情况1： $[j,k]<x[P]$

由结论1可知：$j$ 优于 $k$， $i$ 优于 $j$，$j$ 不是最优的

情况2： $[j,k]>x[P]\mathrm{and}[i,j]>x[P]$

由结论1可知：$k$ 优于 $j$，$j$ 优于 $i$，$j$ 不是最优的

情况2： $[j,k]>x[P]\mathrm{and}[i,j]<x[P]$

由结论1可知：$k$ 优于 $j$，$i$ 优于 $j$，$j$ 不是最优的

结论2得证

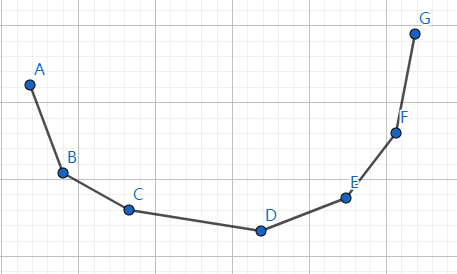
换言之，如果我们吧所有的非最优决策点扔掉，把所有的最优决策点连起来，应该长这样：

是的，一个凹包

凹包的有一个性质：斜率单调递增

因此，我们可以使用一个单调队列来维护斜率来保证斜率的单调性

那么，剩下的做法几乎和普通的单调队列优化一模一样了

代码时间：

#include<cstdio>
#include<algorithm>
using namespace std;
long long int n,dp[2000005],q[2000005],head,tail;
long long int x[2000005],p[2000005],c[2000005];
long long int sum[2000005],sump[2000005];
long long int Up(long long int j,long long int k){			//式子[i,j]的分子部分
	return dp[j]+sum[j]-dp[k]-sum[k];
}
long long int Down(long long int j,long long int k){			式子[i,j]的分母部分
	return sump[j]-sump[k];
}
int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld%lld%lld",&x[i],&p[i],&c[i]);
		sump[i]=sump[i-1]+p[i];
		sum[i]=sum[i-1]+x[i]*p[i];
	}
	for(int i=1;i<=n;i++){
		while(head<tail&&Up(q[head+1],q[head])<=x[i]*Down(q[head+1],q[head])){
			head++;
		}//如果当前队首的决策点已经不是最优的决策点了，就把它扔掉
		 //这里将除法换成了乘法，避免精度问题
		dp[i]=dp[q[head]]+x[i]*(sump[i-1]-sump[q[head]])-sum[i-1]+sum[q[head]]+c[i];			//用最优的决策点进行dp的转移
		while(head<tail&&Up(i,q[tail])*Down(q[tail],q[tail-1])<=Up(q[tail],q[tail-1])*Down(i,q[tail])){
			tail--;
		}//如果新加进来的点会打破凹包结构，就把当前队列里的最后一个点扔掉
		q[++tail]=i;			//加新点
	}
	printf("%lld",dp[n]);			//输出答案
	return 0;
}

现在，我们就完成了此题目。。。吗？

很明显，被Hack了

3.3. 关于这道题目的一些微操（现在可以把万恶的斜率优化扔一边了）

问题出在哪儿呢？

对于 $100\%$ 的数据，保证 $1\le n\le 10^6$，$0\le x_i,p_i,c_i<2^{31}$。

如果光是这样，你还看不出来，那我就给一个特写镜头：

$0\le p_i<2^{31}$

换言之，有可能有一些没有货物的无效工厂

基于此，这里给出三组Hack

Input:
2
0 0 10
1 0 10
Output:
0
Reason:
没有建造仓库的必要

Input:
2
0 10 100
10 0 10
Output:
20
Reason:
在第二个工厂建一个仓库，并把一号工厂里的货物运过去

Input:
2
0 10 10
10 0 100
Output:
10
Reason:
在第一个工厂建一个仓库即可

对于第一个Hack，我们可以进行特判，如果所有的工厂都没有货物，就不用建仓库了

那第二，三个Hack怎么解决呢？

先上代码：

#include<cstdio>
#include<algorithm>
using namespace std;
long long int n,dp[2000005],q[2000005],head,tail,flag,ans=29999823190680;
long long int x[2000005],p[2000005],c[2000005];
long long int sum[2000005],sump[2000005];
long long int Up(long long int j,long long int k){
	return dp[j]+sum[j]-dp[k]-sum[k];
}
long long int Down(long long int j,long long int k){
	return sump[j]-sump[k];
}
int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		scanf("%lld%lld%lld",&x[i],&p[i],&c[i]);
		if(p[i]){
			flag=1;
		}
		sump[i]=sump[i-1]+p[i];
		sum[i]=sum[i-1]+x[i]*p[i];
	}
	if(!flag){			//特判
		printf("0");
		return 0;
	}
	for(int i=1;i<=n;i++){
		while(head<tail&&Up(q[head+1],q[head])<=x[i]*Down(q[head+1],q[head])){
			head++;
		}
		dp[i]=dp[q[head]]+x[i]*(sump[i-1]-sump[q[head]])-sum[i-1]+sum[q[head]]+c[i];
		while(head<tail&&Up(i,q[tail])*Down(q[tail],q[tail-1])<=Up(q[tail],q[tail-1])*Down(i,q[tail])){
			tail--;
		}
		q[++tail]=i;
	}
	for(int i=n;i>=1;i--){
		ans=min(ans,dp[i]);			//下文解释
		if(p[i]){
			printf("%lld",ans);
			return 0;
		}
	}
	return 0;
}

为什么可以这样做呢？

首先，清楚一个事情：对于dp[i]而言，$i$ 号工厂后面的所有工厂我们是暂未考虑的

假设最后一个有货物的工厂编号是 $P$，那么，dp[P-1]是没有考虑 $P$ 号工厂的，而 $P$ 号工厂因为有货物，我们必须考虑它，因此，我们的答案从dp[P]开始尝试更新，后面的所有没有货物的工厂因为可以用来建造仓库，所以是有价值的

因此，最终答案为 a n s = min ⁡ { d p [   i   ] } ( P ≤ i ≤ n ) ans=\min\{dp[\ i\ ]\}(P\le i\le n) ans=min{dp[ i ]}(P≤i≤n)

关于斜率优化，应该就是这些了