【leetcode】力扣刷题笔记 持续更新中
- 推荐资料:[代码随想录](https://programmercarl.com/) 【[leetcode](https://leetcode.cn/)】
- 简单笔记参考
- 0001. Two Sum 【简单】
- 0002. Add Two Numbers 【中等】
- 0015. 3Sum【中等】
- 0017. 电话号码的字母组合【中等】
- 0018. 4Sum【中等】
- 0019. Remove Nth Node From End of List【中等】
- 0020. 有效的括号【简单】
- 0024. Swap Nodes in Pairs【中等】
- 0026. Remove Duplicates from Sorted Array【简单】
- 0027. Remove Element 【简单】
- 0028. Find the Index of the First Occurrence in a String【简单】
- 0034. Find First and Last Position of Element in Sorted Array【中等】
- 0035. Search Insert Position【简单】
- 0037. 解数独【困难】
- 0039. 组合总和【中等】
- 0040. 组合总和 II【中等】
- 0045. 跳跃游戏 II 【中等】
- 0046 全排列【中等】
- 0047. 全排列II【中等】
- 0051. N 皇后【中等】
- 0053. 连续子数组和【中等】
- 0054. Spiral Matrix【中等】
- 0055. 跳跃游戏【中等】
- 0056. 合并区间【中等】
- 0059. Spiral Matrix【中等】
- 0062.【不同路径】
- 0063. 不同路径 II【中等】
- 0069. Sqrt(x)【简单】
- 0070. 爬楼梯【简单】
- 0071. 简化路径【中等】
- 0076. Minimum Window Substring【困难】
- 0077. 组合【中等】
- 0078. 子集【中等】
- 0088. 合并两个有序数组【简单】
- 0090. 子集II【中等】
- 0093. 复原 IP 地址
- 0094. 二叉树的中序遍历【简单】
- 0096. 不同的二叉搜索树【中等】
- 0098. 验证二叉搜索树【简单】
- 0100. 相同的树【简单】
- 0101. 对称二叉树【简单】
- 0102. 二叉树的层序遍历【中等】
- 0104. 二叉树的最大深度【简单】
- 0105. 从前序与中序遍历序列构造二叉树【中等】
- 0106. 从中序与后序遍历序列构造二叉树【中等】
- 0107. 二叉树的层序遍历 II【中等】
- 0108. 将有序数组转化为二叉搜索树【简单】
- 0110. 平衡二叉树【简单】
- 0111. 二叉树的最小深度【简单】
- 0112. 路径总和【简单】
- 0113. 路径总和 II
- 0116. 填充每个节点的下一个右侧指针【中等】
- 0117. 填充每个节点的下一个右侧指针 II【中等】
- 0122. 买卖股票的最佳时机【中等】
- 0121. 买卖股票的最佳时机1【简单】
- 0122. 买卖股票的最佳时机 II 【中等】
- 0122. 路径加密 (LCR)【简单】
- 0123. 买卖股票的最佳时机 III 【中等】
- 0131. 分割回文串【中等】
- 0134. 加油站【中等】
- 0135. 分发糖果【困难】
- 0139. 单词拆分【中等】
- 0142. 环形链表 II【中等】
- 0144. 二叉树的前序遍历【简单】
- 0145. 二叉树的后序遍历【简单】
- 0150. 逆波兰表达式求值【中等】
- 0151. Reverse Word in a String【中等】
- 0160. 相交链表【简单】
- 0188. 买卖股票的最佳时机 IV 【困难】
- 0199. 二叉树的右视图【中等】
- 0202. 快乐数【简单】
- 0203. Remove Linked List Elements【简单】
- 0206. Reverse Linked List【简单】
- 0209. Minimum Size Subarray Sum【中等】
- 0213. 打家劫舍 II【中等】
- 0216. 组合总和 III【中等】
- 0222. 完全二叉树的节点个数【简单】
- 0225. Implement Stack Using Queues【简单】
- 0226. 翻转二叉树【简单】
- 0232. 用栈实现队列【简单】
- 0235. 二叉搜索树的最近公共祖先【中等】
- 0236. 二叉树的最近公共祖先【中等】
- 0239. 滑动窗口最大值【困难】
- 0242. 有效的字母异位词【简单】
- 0257. 二叉树的所有路径【简单】
- 0279. 完全平方数【中等】
- 0283. Move Zeroes【简单】
- 0300. 最长递增子序列【中等】
- 0309. 买卖股票的最佳时机韩冷冻期【中等】
- 0332. 重新安排行程【困难】
- 0337. 打家劫舍
- 0343. 整数拆分【中等】
- 0344. Reverse String【简单】
- 0347. 前 k 个高频元素【中等】
- 0349. 两个数的交集【简单】
- 0350. 两个数组的交集II【简单】
- 0367. Valid Perfect Square【简单】
- 0376. 摆动序列【中等】
- 0377. 组合总和 IV【中等】
- 0383. Ransom Note【简单】
- 0392 判断子序列
- 0404. 左叶子之和【简单】
- 0406. 根据身高重建队列【中等】
- 0416. 分割等和子集【中等】
- 0429. N叉树的层序遍历【中等】
- 0435. 无重叠区间【中等】
- 0450. 删除二叉搜索树中的节点
- 0452. 用最少数量的箭引爆气球【中等】
- 0454. 4Sum II【中等】
- 0474. 一和零【中等】
- 0459. Repeated Substring pattern【简单】
- 0491. 非递减子序列【中等】
- 0494. 目标和 【中等】
- 0501. 二叉搜索树中的众数【简单】
- 0509. 斐波那契数【简单】
- 0518. 零钱兑换 II【中等】
- 0530. 二叉搜索树的最小绝对差【简单】
- 0541. Reverse String II【简单】
- 0559. N 叉树的最大深度
- 0572. 另一棵子树
- 0513. 找树左下角的值【中等】
- 0515. 在每个树行中找最大值【中等】
- 0538. 把二叉搜索树转化为累加树【中等】
- 0637. 二叉树的层平均值【简单】
- 0617. 合并二叉树【简单】
- 0654. 最大二叉树【中等】
- 0674. 最长连续递增子序列【简单】
- 0700. 二叉树中的搜索【简单】
- 0701. 二叉搜索树中的插入操作【中等】
- 0707. Design Linked List【中等】
- 0704. 二分查找【简单】
- 0714. 买卖股票的最佳时机含手续费
- 0718. 最长连续子数组【中等】
- 0738. 单调递增的数字【中等】
- 0746. 使用最小花费爬楼梯【简单】
- 0763. 划分字母区间【中等】
- 0844. Backspace String Compare【简单】
- 0860. 柠檬水找零【简单】
- 0904. Fruit Into Backets【中等】
- 0968. 监督二叉树
- 0977. Squares of a Sorted Array【简单】
- 1005. K 次取反后最大化的数组和【简单】
- 1035 .
- 1047. 删除字符串中所有相邻重复项
- 1049. 最后一块石头的重量【中等】
- 1143. 最长公共子序列
推荐资料:代码随想录 【leetcode】
简单笔记参考
数组篇
数组理论基础
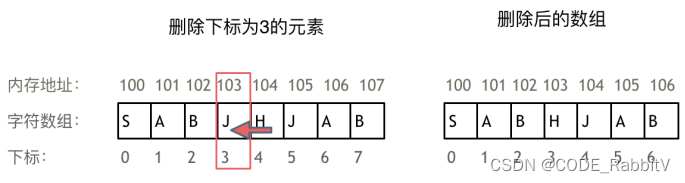
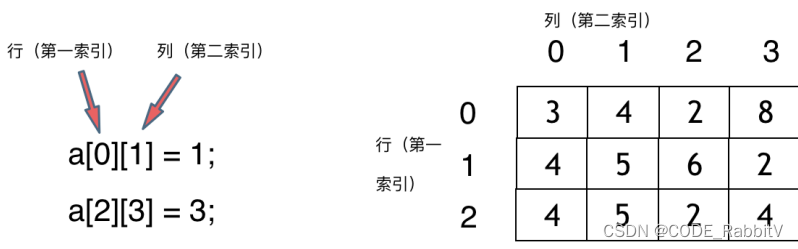
- 数组:存放在连续内存空间上的相同类型数据的集合,所以数组可以⽅便的通过下标索引的⽅式获取到下标下对应的数据
二分查找【转 No.0704】
给定⼀个 n 个元素有序的(升序)整型数组 nums 和⼀个⽬标值 target ,写⼀个函数搜索 nums 中的 target,如果⽬标值存在返回下标,否则返回 -1。
双指针法【转 No.0027】
移除元素:给你⼀个数组 nums 和⼀个值 val,你需要 原地(不使用额外的数组空间) 移除所有数值等于 val 的元素,并返回移除后数组的新⻓度。
- 数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。
滑动窗口法【转 No.0209】
类似双指针,是不断的调节⼦序列的起始位置和终⽌位置,从⽽得出我们要想的结果
只有一个 for 循环,循环因子表示目标区间终止位置;起始位置动态移动
- 窗⼝内是什么?目标区间
- 如何移动窗⼝的起始位置?该缩小时
- 如何移动窗⼝的结束位置?逐渐向后遍历
螺旋矩阵【转 No.0059】
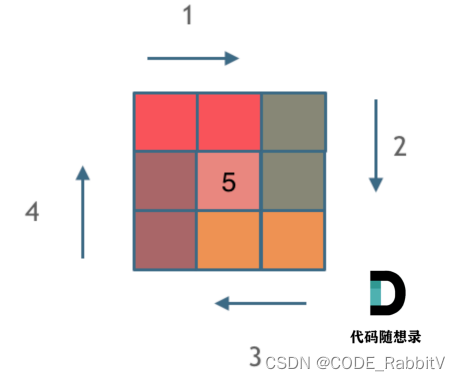
模拟顺时针画矩阵的过程:
- 填充上⾏从左到右
- 填充右列从上到下
- 填充下⾏从右到左
- 填充左列从下到上
由外向内⼀圈⼀圈这么画下去。
时间复杂度 O ( n 2 ) O(n^2) O(n2), 空间复杂度 O ( 1 ) O(1) O(1)
链表篇
列表基础理论【转 No.0203】
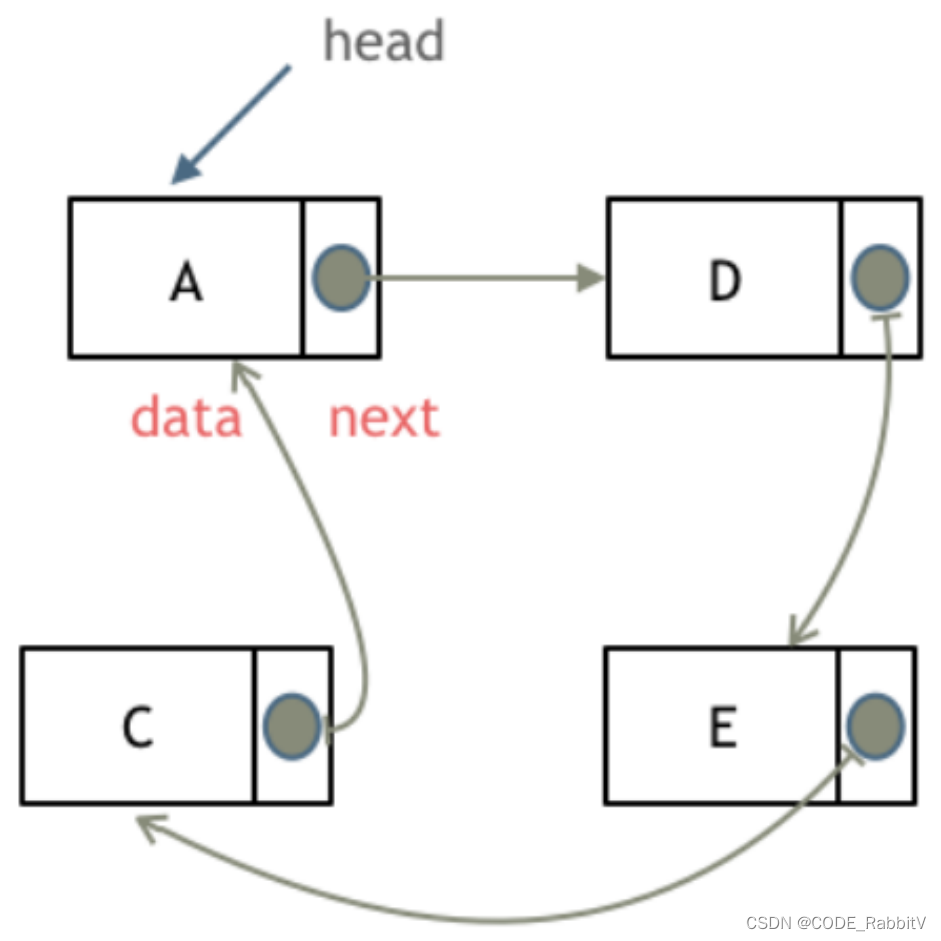
链表的类型:
- 单链表
- 双链表
- 循环链表
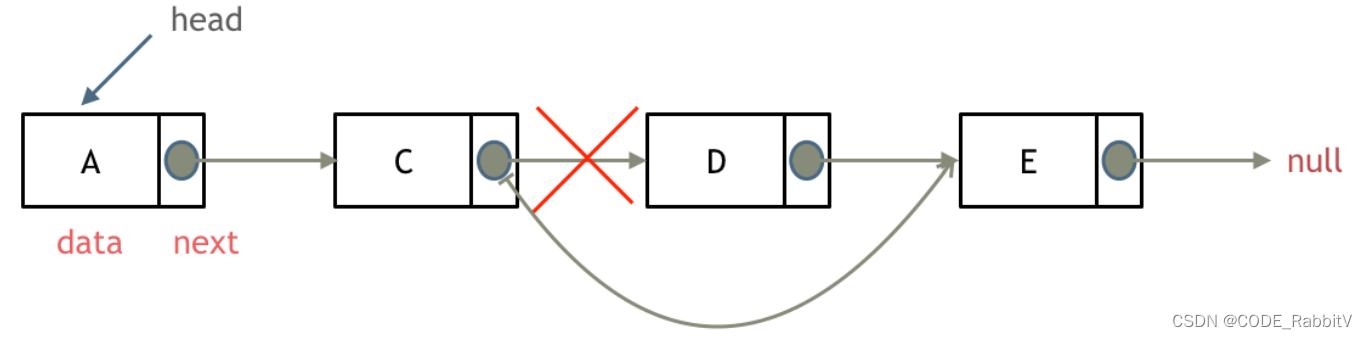
链表操作 - 删除节点:将当前节点
前一节点的 next 指针指向当前节点后一节点(python 有自己的内存回收机制,不用手动释放被删除节点)
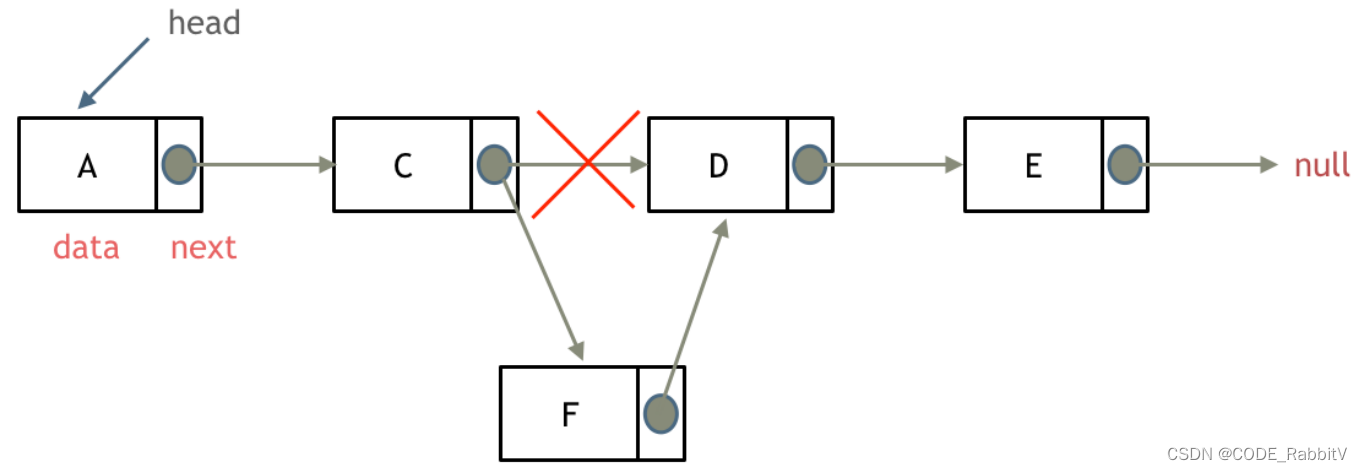
- 添加节点:删除和添加都很简单(
O(1)),但是查找到操作位置较慢(O(n))
和数组对比
数组:插入/删除O(n)查询O(1),适用于数据量固定,频繁查询,较少增删
链表:插入/删除O(1)查询O(n),适用于数据量固定,频繁增删,较少查询
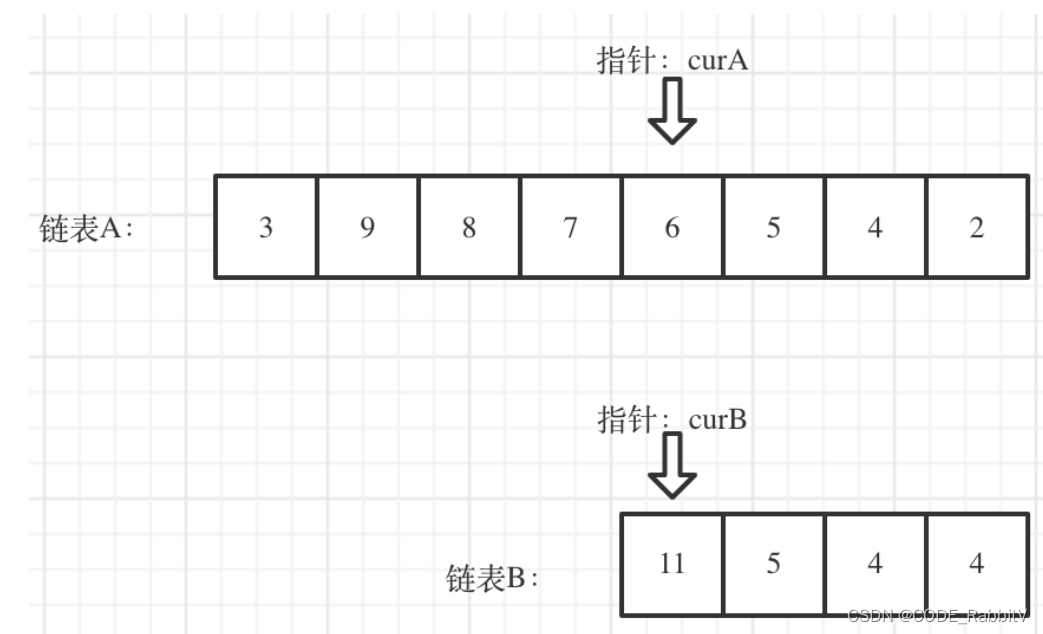
链表相交【转 No.0019】
求出两个链表的⻓度,并求出两个链表⻓度的差值,然后让curA移动到,和curB 末尾对⻬的位置,如图
然后就可以开始逐个比较
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
def get_len(head):
current = head
len_result = 0
while current:
current = current.next
len_result += 1
return len_result
len_A = get_len(headA)
len_B = get_len(headB)
current_A = headA
current_B = headB
if not current_A:
return None
if len_A >= len_B:
move_step = len_A - len_B
while move_step:
current_A = current_A.next
move_step -= 1
else:
move_step = len_B - len_A
while move_step:
current_B = current_B.next
move_step -= 1
# 上述已移动到同一位置,可以进行逐个比较
while current_A:
if current_A == current_B:
return current_A
current_A = current_A.next
current_B = current_B.next
环形链表【转 No.0142】
- 判断链表是否环
- 如果有环,如何找到这个环的入口
哈希表
哈希表理论基础 hash table
常见的三种哈希结构:数组(list)、集合(set)、映射(map)
适合的问题场景:判断一个元素是否出现过
什么时候使⽤哈希法,当我们需要查询⼀个元素是否出现过,或者⼀个元素是否在集合⾥的时候,就要第⼀时间想到哈希法
字符串
KMP 算法:解决字符串匹配
前(后)缀表:包含首(尾)字母不包含尾(首)字母的所有子串
a a b a a f
0 1 0 1 2 0
求最长相等前后缀长度: 2,遇到冲突(不匹配)时,需要回退到的(模式串的)位置
!!! 卡了我一星期的 KMP 终于懂了 -> KMP讲解
二叉树
二叉树的种类:满二叉树和完全二叉树- 满⼆叉树:只有度为0的结点和度为2的结点,并且度为0的结点在同⼀层上;深度为
k的结点数量为2^k-1 - 完全二叉树:除了最底层节点可能没填满外,其余每层节点数都达到最⼤值,并且最下⾯⼀层的节点都集中在该层最左边的若⼲位置
- 二叉搜索树:对结构没要求;但是元素放置是左小右大
- 平衡二叉搜索树:左右两个⼦树的⾼度差的绝对值不超过1,并且左右两个⼦树都是⼀棵平衡⼆叉树
- 满⼆叉树:只有度为0的结点和度为2的结点,并且度为0的结点在同⼀层上;深度为
二叉树的存储方式:链式存储和顺序存储二叉树的遍历方式:深度优先遍历和广度优先遍历- 深度:前序(中 x x;从上往下求深度)、中序( x 中 x)、后序(x x 中; 从下往上遍历求高度)
- 广度:层次遍历
递归
确定递归函数的参数和返回值:确定哪些参数是递归的过程中需要处理的, 并且还要明确每次递归的返回值是什么进⽽确定递归函数的返回类型确定终⽌条件:写完了递归算法, 运⾏的时候,经常会遇到栈溢出的错误,就是没写终⽌条件或者终⽌条件写的不对,操作系统也是⽤⼀个栈的结构来保存每⼀层递归的信息,如果递归没有终⽌,操作系统的内存栈必然就会溢出。确定单层递归的逻辑:确定每⼀层递归需要处理的信息。在这⾥也就会᯿复调⽤⾃⼰来实现递归的过程。
回溯算法
只要有递归,就会有回溯;回溯的本质是穷举,所以效率较低,通过剪枝加速
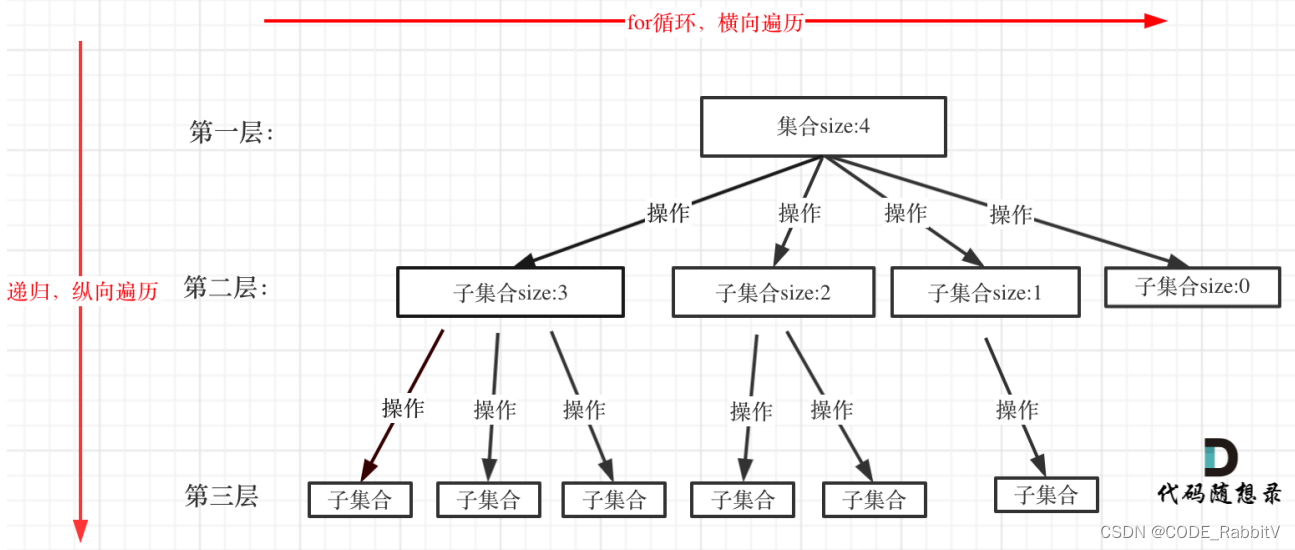
回溯法,⼀般可以解决如下⼏种问题【回溯法解决的问题都可以抽象为树形结构,树的宽度为处理的集合大小,树的深度为递归的深度】:
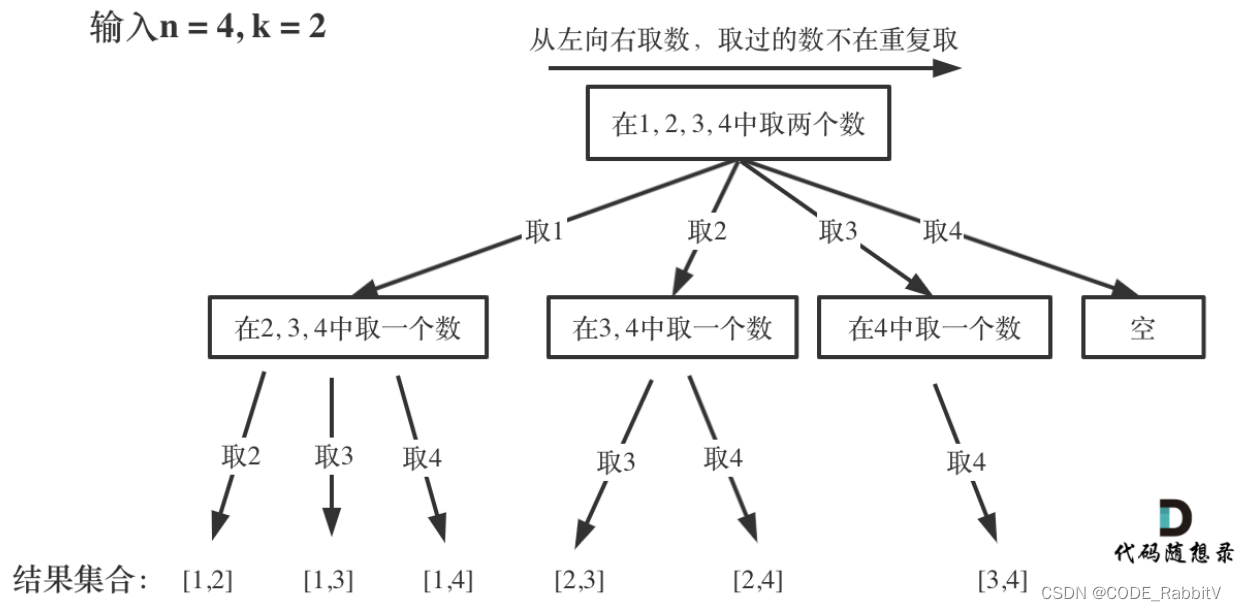
组合问题:N个数⾥⾯按⼀定规则找出k个数的集合
切割问题:⼀个字符串按⼀定规则有⼏种切割⽅式
⼦集问题:⼀个N个数的集合⾥有多少符合条件的⼦集
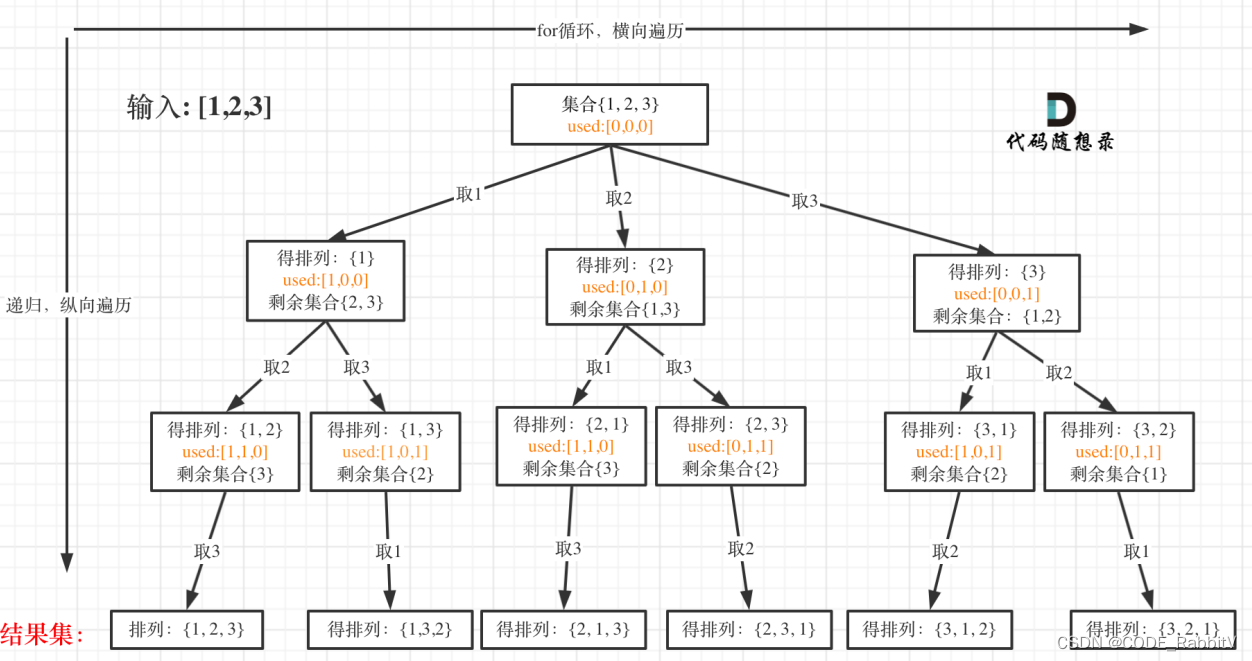
排列问题:N个数按⼀定规则全排列,有⼏种排列⽅式
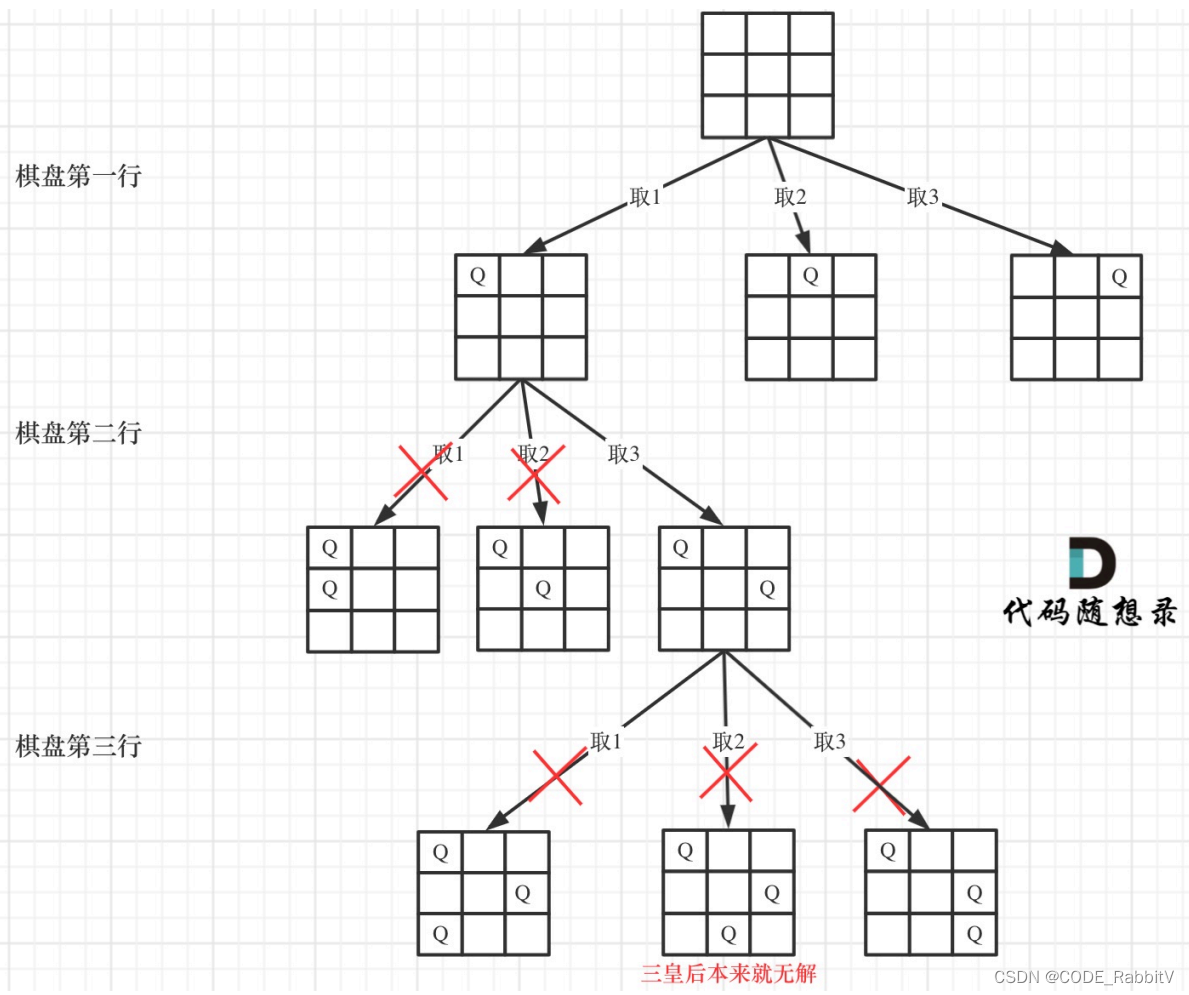
棋盘问题:N皇后,解数独等等
一般而言,递归函数 backtracking 没有返回值,参数一般比较多;
动态规划
五步曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
debug 思路:把dp数组打印出来,看看究竟是不是按照⾃⼰思路推导的!
背包问题:
01 背包
-
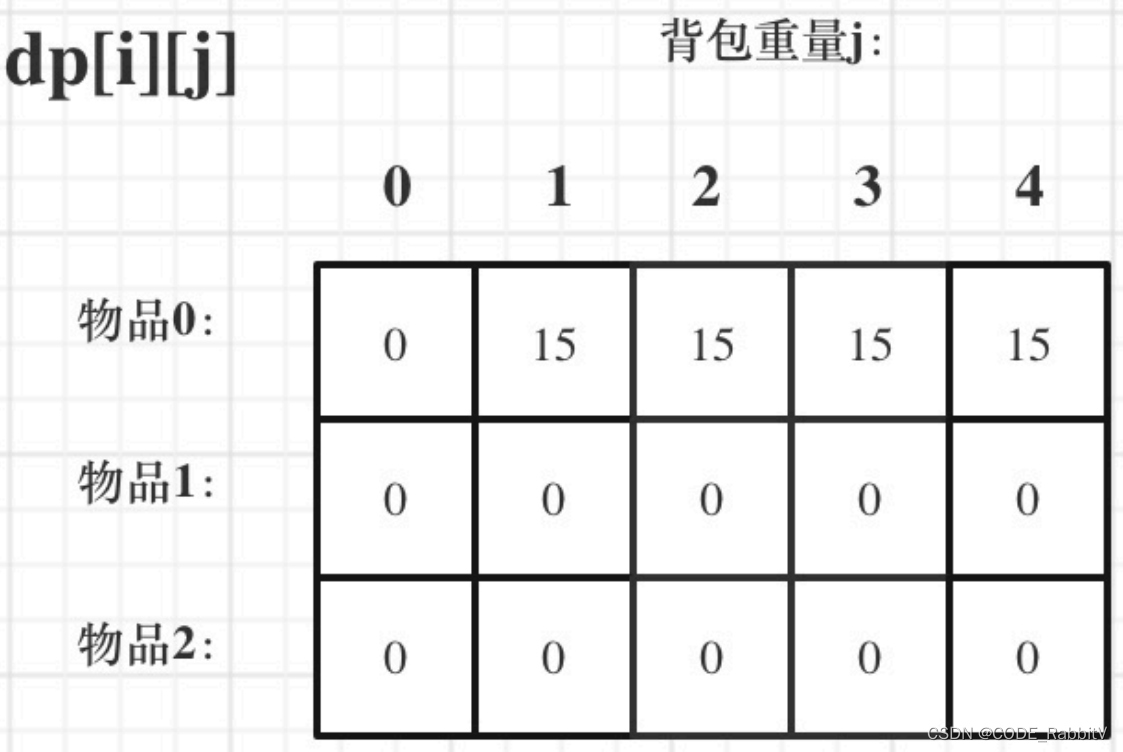
不放物品i:由dp[i - 1][j]推出,即背包容量为j,⾥⾯不放物品i的最⼤价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量⼤于背包j的重量时,物品i⽆法放进背包中,所以背包内的价值依然和前⾯相同。)
-
放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最⼤价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最⼤价值
-
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
01 背包和完全背包的区别仅在于遍历物品时候倒序使得每个物品可以被加入多次
0001. Two Sum 【简单】
# solution 1: 暴力枚举
# 时间复杂度 O(n^2), 时间复杂度 O(1)
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for i in range(len(nums)):
for j in range(i+1, len(nums)):
if nums[i] + nums[j] == target:
return [i, j]
return [] ##
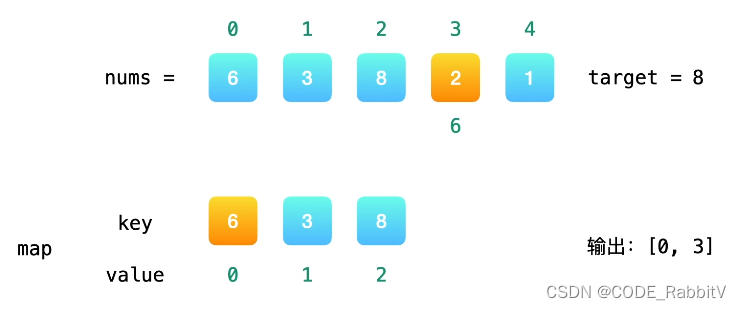
如图,原先第一次遍历过的 num (和对应的 index) 存下来,避开第二次遍历;用空间换时间
想清楚map中的key和value⽤来存什么的,会使得写代码的思路更加清晰
# solution 2: 哈希表法
# 时间复杂度 O(n), 空间复杂度 O(n)
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
my_hash = {}
## 因为既用到了 i 又用到了 nums[i]
## 所以可以用 for i, num in enumerate(nums) 简化代码
for i in range(len(nums)):
if target - nums[i] in my_hash:
return [i, my_hash[target - nums[i]]]
else:
my_hash[nums[i]] = i
0002. Add Two Numbers 【中等】
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
# solution 1: ListNode 转 整数加法 转 ListNode
# 时间复杂度 O(len(l1)+len(l2)), 空间复杂度 O(max(len(l1),len(l2)))
def get_num(l: Optional[ListNode]) -> Optional[int]:
num = 0
ratio = 1
temp = l
while 1:
num += temp.val * ratio
ratio *= 10
if temp.next == None:
break
temp = temp.next
return num
class Solution:
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
# get the sum of num1 and num2, from l1 and l2
num3 = get_num(l1)+ get_num(l2)
# get values for new ListNode
num3_list = []
while num3:
num3_list.insert(0, num3%10)
num3 //= 10
if num3_list == []:
num3_list = [0]
# build new ListNode
temp_l = None
for i in range(len(num3_list)):
temp_l = ListNode(num3_list[i], temp_l)
return temp_l
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
# solution 2: 根据加法原理逐位计算
# 时间复杂度 O(max(len(l1),len(l2))), 空间复杂度 O(1)
class Solution:
def updata_temp(self, temp, new_value):
return (1, temp+new_value-10) if temp+new_value>=10 else (0, temp+new_value)
def addTwoNumbers(self, l1: Optional[ListNode], l2: Optional[ListNode]) -> Optional[ListNode]:
s_node = ListNode(0)
l3=s_node
temp = 0
while True:
if l1 == None and l2 == None:
if temp:
new_node = ListNode(temp, None)
l3.next = new_node
return s_node.next
if l1 == None and not l2 == None:
temp, new_value = self.updata_temp(temp, l2.val)
new_node = ListNode(new_value, None)
l3.next = new_node
l3 = new_node
l2 = l2.next
if l2 == None and not l1 == None:
temp, new_value = self.updata_temp(temp, l1.val)
new_node = ListNode(new_value, None)
l3.next = new_node
l3 = new_node
l1 = l1.next
if not l1 == None and not l2 == None:
temp, new_value = self.updata_temp(temp, l1.val+l2.val)
new_node = ListNode(new_value, None)
l3.next = new_node
l3 = new_node
l1 = l1.next
l2 = l2.next
0015. 3Sum【中等】
用哈希表法,涉及去重比较麻烦, 可以用双指针法
class Solution:
def threeSum(self, nums: List[int]) -> List[List[int]]:
nums.sort()
result = []
for i in range(len(nums)):
if nums[i] > 0:
return result
if i > 0 and nums[i] == nums[i-1]: # 去重第一个数
continue
l = i+1
r = len(nums) - 1
while r > l:
if nums[i] + nums[l] + nums[r] > 0:
r -= 1
elif nums[i] + nums[l] + nums[r] < 0:
l += 1
else:
result.append([nums[i], nums[l], nums[r]])
while r>l and nums[r] == nums[r-1]: # 去重第二个数
r-=1
while r>l and nums[l] == nums[l+1]: # 去重第三个数
l+=1
r -= 1
l += 1
return result
0017. 电话号码的字母组合【中等】
要解决如下三个问题:
- 数字和字⺟如何映射
- 两个字⺟就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来 ->
回溯法来解决n个for循环的问题 - 输⼊1 * #按键等等异常情况
class Solution:
def __init__(self, ):
self.letterMap = [
"", # 0
"", # 1
"abc", # 2
"def", # 3
"ghi", # 4
"jkl", # 5
"mno", # 6
"pqrs", # 7
"tuv", # 8
"wxyz", # 9
]
self.path = []
self.result = []
def backtracking(self, digits, idx):
if idx == len(digits):
temp = ''.join(self.path)
if temp:
self.result.append(temp) ## .copy()
return
for i in self.letterMap[int(digits[idx])]:
self.path.append(i)
self.backtracking(digits, idx+1)
self.path.pop(-1)
def letterCombinations(self, digits: str) -> List[str]:
self.backtracking(digits, 0)
return self.result
0018. 4Sum【中等】
四数之和,和 No.15. 三数之和是⼀个思路,都是使⽤双指针法, 基本解法就是在15.三数之和 的基础上再套⼀层for循环
三数之和的双指针解法是⼀层for循环num[i]为确定值,然后循环内有left和right下标作为双指针,找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值,依然是循环内有left和right下标作为双指针, 找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况,三数之和的时间复杂度是O(n^2) 四数之和的时间复杂度是O(n^3) 。
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
nums.sort()
result = []
for k in range(len(nums)):
# if nums[i] > target : # 不能这么写,target 可能是负数
# return result
if k > 0 and nums[k] == nums[k-1]: # 去重第一个数
continue
for i in range(k+1, len(nums)):
if i > k+1 and nums[i] == nums[i-1]: # 去重第二个数
continue
l = i+1
r = len(nums) - 1
while r > l:
if nums[k] + nums[i] + nums[l] + nums[r] > target:
r -= 1
elif nums[k] + nums[i] + nums[l] + nums[r] < target:
l += 1
else:
result.append([nums[k], nums[i], nums[l], nums[r]])
while r>l and nums[r] == nums[r-1]: # 去重第三个数
r-=1
while r>l and nums[l] == nums[l+1]: # 去重第四个数
l+=1
r -= 1
l += 1
return result
0019. Remove Nth Node From End of List【中等】
考察链表下的双指针应⽤:如果要删除倒数第n个节点,让fast移动n步,然后让fast和slow同时移动,直到fast指向链表末尾。删掉slow所指向的节点就可以了。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:
dumyhead = ListNode(0, head)
fast = dumyhead
slow = dumyhead
while n:
fast = fast.next
n -= 1
while fast and fast.next: # 移动到删除位置
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return dumyhead.next
0020. 有效的括号【简单】
考察栈操作;最后都弹出了,则说明有效
class Solution:
def isValid(self, s: str) -> bool:
result = []
temp_dict = {')':'(', '}': '{', ']':'['}
for ss in s:
if not result:
result.append(ss)
else:
if ss in temp_dict.keys() and result[-1] == temp_dict[ss]: # 匹配上了一对则弹出
result.pop()
else:
result.append(ss)
return not result
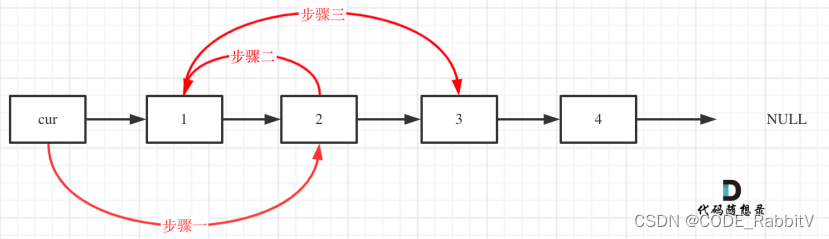
0024. Swap Nodes in Pairs【中等】
考察链表操作,同 0203;分段操作,注意和上一段连接起来
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def swapPairs(self, head: Optional[ListNode]) -> Optional[ListNode]:
new_head = ListNode(0,head)
current = new_head
while current.next and current.next.next: # 分别为 奇数长度和偶数长度 的终止条件
temp1 = current.next
temp3 = current.next.next.next
current.next = current.next.next
current.next.next = temp1
temp1.next = temp3
current = temp1
return new_head.next
0026. Remove Duplicates from Sorted Array【简单】
考察双指针法,同 0027,只是筛选新数组元素的条件不同,可以根据题目中有序数组的限定,利用nums[slow] 进行判定
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
slow = 0
for fast in range(1, len(nums)):
if nums[fast] == nums[slow]: ## 利用`nums[slow]` 进行判定
continue
slow += 1
nums[slow] = nums[fast]
return slow+1
0027. Remove Element 【简单】
# Solution 1: 暴力解法
# 时间复杂度 O(n^2), 空间复杂度 O(1)
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
k = 0
for i in range(len(nums)):
## 移动后的 i 位置上的新元素可能还是需要删除的 val 故需要 while 处理
while i+k < len(nums) and nums[i] == val:
for j in range(i+1, len(nums)):
nums[j-1] = nums[j]
k += 1 # find new element "val"
return len(nums) - k
或者将上述两层 for 替换为双指针法:通过一个个快指针和慢指针在⼀个for循环下完成两个for循环的⼯作 (用原数组空间位置 造一个新的数组)
- 快指针:寻找新数组的元素 ,新数组就是不含有⽬标元素的数组
- 慢指针:指向更新新数组下标的位置
# Solution 2: 双指针法
# 时间复杂度 O(n), 空间复杂度 O(1)
class Solution:
def removeElement(self, nums: List[int], val: int) -> int:
slow = 0
for fast in range(len(nums)):
if not nums[fast]==val:
nums[slow] = nums[fast]
slow += 1
return slow
0028. Find the Index of the First Occurrence in a String【简单】
考察字符串匹配算法 KMP,其中 get_next 和主流程的逻辑基本一致
class Solution:
def strStr(self, haystack: str, needle: str) -> int:
def get_next(needle):
j = 0
next = [0]
for i in range(1, len(needle)):
while j>0 and needle[j] != needle[i]:
j = next[j-1]
if needle[i] == needle[j]:
j+=1
next.append(j)
return next
next = get_next(needle)
j = 0
for i in range(len(haystack)):
while j > 0 and haystack[i] != needle[j]:
j = next[j-1]
if haystack[i] == needle[j]:
j+=1
if j == len(needle):
return i-j +1
return -1
0034. Find First and Last Position of Element in Sorted Array【中等】
考察二分查找,同 0704,先掌握 0704
只是 target 会出现多次,找到后还需要继续寻找 target 区间边界
- 如果找到后开始线性查找,复杂度高 不满足题目要求的
O(log n),故仍需继续采用二分查找# !!错误示例,找到 middle 后,线性查找 # 时间复杂度 O(logn), 空间复杂度 O(1) ll = middle while ll-1 >=0 and nums[ll-1] == target: ll -= 1 rr = middle while rr+1 <=len(nums)-1 and nums[rr+1] == target: rr += 1 return [ll,rr] - 正确做法应该为修改:找到 middle,继续寻找
target区间边界,重点修改代码如下# 分别寻找左边界和右边界 # 左边界 ll1, rr1 = left, middle mm1 = ll1 + (rr1-ll1) // 2 while ll1 < mm1: print(ll1,rr1,mm1) if nums[mm1] < target: ll1 = mm1 + 1 else: assert(nums[mm1] == target) rr1 = mm1 mm1 = ll1 + (rr1-ll1) // 2 if not nums[ll1] == target: ## 应对退出时 该区间内唯一 target 值不位于左侧的情况 ll1=rr1 # 右边界 ll2, rr2 = middle, right mm2 = ll2 + (rr2-ll2) // 2 while ll2 < mm2: print(ll2,rr2,mm2) if nums[mm2] > target: rr2 = mm2 - 1 else: assert(nums[mm2] == target) ll2= mm2 mm2 = ll2 + (rr2-ll2) // 2 if nums[rr2] == target: ## 应对退出时 该区间内右边界也是 target 值的情况 ll2=rr2 return [ll1,ll2]
0035. Search Insert Position【简单】
考察二分查找,同 0704,先掌握 0704
只是在未找到,返回插入位置的情况下,最后一行代码不同,改为 return left
0037. 解数独【困难】
class Solution:
def is_valid(self, row: int, col: int, val: int, board: List[List[str]]) -> bool:
# 判断同一行是否冲突
for i in range(9):
if board[row][i] == str(val):
return False
# 判断同一列是否冲突
for j in range(9):
if board[j][col] == str(val):
return False
# 判断同一九宫格是否有冲突
start_row = (row // 3) * 3
start_col = (col // 3) * 3
for i in range(start_row, start_row + 3):
for j in range(start_col, start_col + 3):
if board[i][j] == str(val):
return False
return True
def backtracking(self, board: List[List[str]]) -> bool:
for i in range(len(board)): # 遍历行
for j in range(len(board[0])): # 遍历列
if board[i][j] != '.': continue # 若空格内已有数字,跳过
for k in range(1, 10):
if self.is_valid(i, j, k, board):
board[i][j] = str(k)
if self.backtracking(board): return True
board[i][j] = '.'
return False # 无解
return True # 有解
def solveSudoku(self, board: List[List[str]]) -> None:
self.backtracking(board)
0039. 组合总和【中等】
class Solution:
def __init__(self):
self.path = []
self.result = []
self.current_sum = 0
def backtracking(self, candidates, target, start_idx):
if self.current_sum > target: ## 剪枝
return
if self.current_sum == target:
self.result.append(self.path.copy()) ## .copy()
return
for i_idx, i in enumerate(candidates[start_idx: ]):
self.path.append(i)
self.current_sum += i
self.backtracking(candidates, target, i_idx+start_idx) ## 能重复故不 +1
self.path.pop(-1)
self.current_sum -= i
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
self.backtracking(candidates, target, 0)
return self.result
0040. 组合总和 II【中等】
class Solution:
def __init__(self):
self.path = []
self.result = []
self.current_sum = 0
self.used = None
def backtracking(self, candidates, target, start_idx):
if self.current_sum > target: ## 剪枝
return
if self.current_sum == target:
self.result.append(self.path.copy()) ## .copy()
return
for i_idx, i in enumerate(candidates[start_idx: ]):
# used[i - 1] == true,说明同⼀树枝candidates[i - 1]使⽤过
# used[i - 1] == false,说明同⼀树层candidates[i - 1]使⽤过
if i_idx > 0 and candidates[start_idx+i_idx]==candidates[start_idx+i_idx-1] and self.used[start_idx+i_idx-1]==False: ## 去重
continue
self.path.append(i)
self.current_sum += i
self.used[i_idx+start_idx] = True ## 去重
self.backtracking(candidates, target, i_idx+start_idx+1)
self.path.pop(-1)
self.current_sum -= i
self.used[i_idx+start_idx] = False ## 去重
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
candidates.sort() ## 去重
self.used = [False] * len(candidates)
self.backtracking(candidates, target, 0)
return self.result
0045. 跳跃游戏 II 【中等】
class Solution:
def jump(self, nums: List[int]) -> int:
if len(nums) == 1: return 0 ## 特例
max_range = 0
step_num = 0
current_range = 0
for nn_idx, nn in enumerate(nums):
if nn_idx > max_range: return False ## 覆盖失败
if nn+nn_idx > max_range:
max_range = nn+nn_idx
if nn_idx == current_range: ## 需要加油
current_range = max_range
step_num += 1
if max_range >= len(nums)-1: return step_num ## 覆盖成功
0046 全排列【中等】
组合用 startidx 排列用 used
class Solution:
def __init__(self):
self.path = []
self.result = []
self.used = [] ## 去重
def backtracking(self, candidates):
if len(self.path) == len(candidates):
self.result.append(self.path.copy()) # 每次都加入,而不是只加入叶子
for i_idx, i in enumerate(candidates):
if self.used[i_idx]: ## 去重
continue
self.path.append(i)
self.used[i_idx] = True
self.backtracking(candidates)
self.path.pop(-1)
self.used[i_idx] = False
def permute(self, nums: List[int]) -> List[List[int]]:
self.used = [False]*len(nums) ## 去重
self.backtracking(nums)
return self.result
0047. 全排列II【中等】
同理组合中的结果去重方法
class Solution:
def __init__(self):
self.path = []
self.result = []
self.used = []
def backtracking(self, candidates):
if len(self.path) == len(candidates):
self.result.append(self.path.copy())
for i_idx, i in enumerate(candidates):
if self.used[i_idx]:
continue
if i_idx and candidates[i_idx] == candidates[i_idx-1] and self.used[i_idx-1]==False: #### 新增
continue
self.path.append(i)
self.used[i_idx] = True
self.backtracking(candidates)
self.path.pop(-1)
self.used[i_idx] = False
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
nums.sort() #### 新增
self.used = [False]*len(nums)
self.backtracking(nums)
return self.result
0051. N 皇后【中等】
import copy
class Solution:
def __init__(self):
self.chessboard = []
self.results = []
def isValid(self, row, col):
# 检查列
for i in range(row):
if self.chessboard[i][col] == 'Q':
return False # 当前列已经存在皇后,不合法
# 检查 45 度角是否有皇后
i, j = row - 1, col - 1
while i >= 0 and j >= 0:
if self.chessboard[i][j] == 'Q':
return False # 左上方向已经存在皇后,不合法
i -= 1
j -= 1
# 检查 135 度角是否有皇后
i, j = row - 1, col + 1
while i >= 0 and j < len(self.chessboard):
if self.chessboard[i][j] == 'Q':
return False # 右上方向已经存在皇后,不合法
i -= 1
j += 1
return True # 当前位置合法
def backtracking(self, n, row):
if row == n:
self.results.append(copy.deepcopy(self.chessboard[:]))
return
for col in range(n):
if self.isValid(row, col):
self.chessboard[row][col] = 'Q'
self.backtracking(n, row+1)
self.chessboard[row][col] = '.'
def solveNQueens(self, n: int) -> List[List[str]]:
self.chessboard = [['.'] * n for _ in range(n)]
self.backtracking(n, 0)
return [[''.join(row) for row in solution] for solution in self.results]
0053. 连续子数组和【中等】
# 贪心解法
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
current_sum = None
result = nums[0]
for nn in nums:
current_sum = current_sum + nn if current_sum is not None else nn
if current_sum > result: ## 更新 result
result = current_sum
if current_sum < 0: ## 重置累加和
current_sum = None
return result
0054. Spiral Matrix【中等】
考察螺旋矩阵,但是长款不等,需要考虑的情况更多,重点看下半部分
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
m = len(matrix)
n = len(matrix[0])
i = 0
j = 0
results = []
if min(m , n) >= 2: # 正常获取完整四周
for n_index in range( min(m // 2, n // 2) ):
for jj in range(j,n-n_index-1): # 上
results.append(matrix[i][jj])
j = jj + 1
for ii in range(i,m-n_index-1): # 右
results.append(matrix[ii][j])
i = ii + 1
for jj in range(j, n_index, -1): # 下
results.append(matrix[i][jj])
j = jj - 1
for ii in range(i, n_index, -1): # 左
results.append(matrix[ii][j])
i = ii - 1
# 准备进入下一圈
i += 1
j += 1
# 主要是这部分会出错,考虑不全
if m <= n:
if m % 2 == 1: # 处理只有上边的特殊情况
results.append(matrix[i][j])
j += 1
for aa in range(n-m):
results.append(matrix[i][j+aa])
else:
if n % 2 == 1: # 处理只有左边的特殊情况
results.append(matrix[i][j])
i += 1
for aa in range(m-n):
results.append(matrix[i+aa][j])
return results
0055. 跳跃游戏【中等】
贪⼼算法局部最优解:每次取最⼤跳跃步数(取最⼤覆盖范围),整体最优解:最后得到整体最⼤覆盖范围,看是否能到终点
class Solution:
def canJump(self, nums: List[int]) -> bool:
max_range = 0
for nn_idx, nn in enumerate(nums):
if nn_idx > max_range: return False ## 覆盖失败
max_range = max(max_range, nn+nn_idx)
if max_range >= len(nums)-1: return True ## 覆盖成功
0056. 合并区间【中等】
class Solution:
def merge(self, intervals: List[List[int]]) -> List[List[int]]:
sorted_points = sorted(intervals, key=lambda x: x[0])
for pp_idx, pp in enumerate(sorted_points):
if pp_idx == 0:
result = [sorted_points[0]]
continue
if pp[0] <= result[-1][1]: # 最大右而不是气球问题中的最小右
result[-1][1] = max(pp[1], result[-1][1])
else:
result.append(pp)
return result
0059. Spiral Matrix【中等】
考察螺旋矩阵,注意拐角位置处理权的分配即可
class Solution:
def generateMatrix(self, n: int) -> List[List[int]]:
result = [[n*n] * n for nn in range(n)]
i = 0
j = 0
temp = 1
for n_index in range( n // 2 ):
for jj in range(j,n-n_index-1): # 上
result[i][jj] = temp
temp += 1
j = jj + 1
for ii in range(i,n-n_index-1): # 右
result[ii][j] = temp
temp += 1
i = ii + 1
for jj in range(j, n_index, -1): # 下
result[i][jj] = temp
temp += 1
j = jj - 1
for ii in range(i, n_index, -1): # 左
result[ii][j] = temp
temp += 1
i = ii - 1
# 准备进入下一圈
i += 1
j += 1
return result
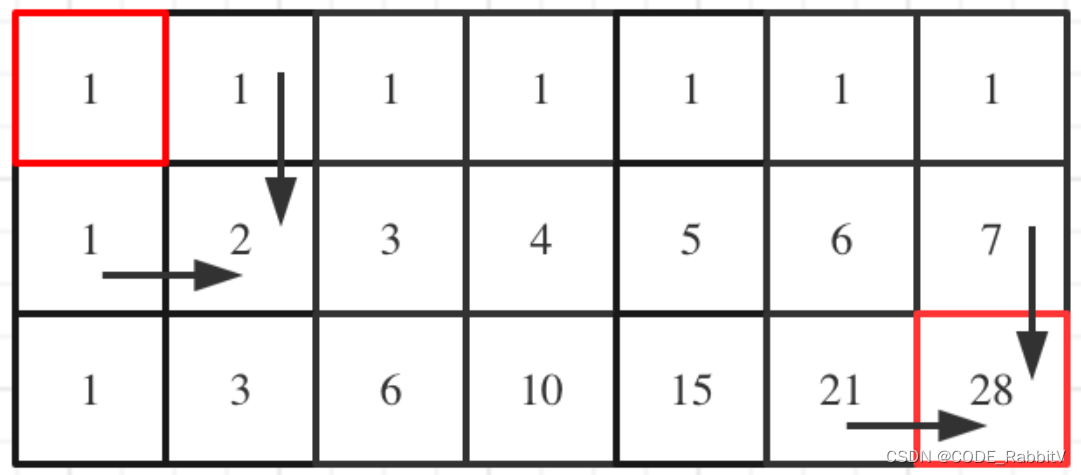
0062.【不同路径】
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
import numpy as np
dp = np.ones((m,n), dtype=int)
for i in range(1, m):
for j in range(1, n):
dp[i,j] = dp[i-1,j] + dp[i,j-1]
return int(dp[-1,-1])
0063. 不同路径 II【中等】
考虑障碍,在遇到障碍后,后面的位置都置 0
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
if obstacleGrid[0][0]: return 0
m = len(obstacleGrid)
n = len(obstacleGrid[0])
import numpy as np
dp = np.zeros((m,n), dtype=int)
for i in range(m):
if not obstacleGrid[i][0]: dp[i,0] = 1 ##
else: break
for j in range(n):
if not obstacleGrid[0][j]: dp[0,j] = 1 ##
else: break
for i in range(1, m):
for j in range(1, n):
dp[i,j] = dp[i-1,j]+dp[i,j-1] if not obstacleGrid[i][j] else 0 ##
return int(dp[-1,-1])
0069. Sqrt(x)【简单】
考察二分查找,同 0704,先掌握 0704
只是在未找到,返回结果的情况下,因为结果要求向下取整,所以 return left-1
# 时间复杂度 O(logx), 空间复杂度 O(1)
class Solution:
def mySqrt(self, x: int) -> int:
left, right = 0, x
while left <= right:
middle = left + (right-left)//2
if middle*middle < x:
left = middle + 1
elif middle*middle > x:
right = middle - 1
else:
return middle
return left-1
0070. 爬楼梯【简单】
同 509 斐波那契数列
class Solution:
def climbStairs(self, n: int) -> int:
self.solution = [0, 1, 2]
for i in range(3, n+1):
self.solution.append(self.solution[i-1]+self.solution[i-2])
return self.solution[n]
0071. 简化路径【中等】
考察栈的使用
class Solution:
def simplifyPath(self, path: str) -> str:
parts = path.split('/') # 分割原路径
temp = [] # 存有效路段
for p in parts:
if p == '.' or p == '':
continue
if p == '..':
if temp:
temp.pop()
else:
temp.append(p)
return '/'+'/'.join(temp) # 拼凑所需结果
0076. Minimum Window Substring【困难】
考察滑动窗口法,同 0209,需要注意的是,在本题中,满足一定条件后(找到当前有边界下的符合条件的子串),才开始(逐步向右)移动左窗口
class Solution:
def minWindow(self, s: str, t: str) -> str:
i = 0
result = ''
window_count = Counter()
target_count = Counter(t)
can_move = 0
for j in range(len(s)):
window_count[s[j]] += 1
if s[j] in target_count and window_count[s[j]] == target_count[s[j]]:
can_move += 1
if not can_move == len(target_count): # 满足条件才开始考虑左边界移动
continue
while 0<=i<=j:
if s[i] not in target_count: # 当前元素为不相关元素,安全移动
temp_result = s[i:j+1]
if result =='' or len(result) > len(temp_result):
result = temp_result
window_count[s[i]]-=1
i+=1
continue
if s[i] in target_count:
if window_count[s[i]] >= target_count[s[i]]: # 当前元素为相关元素,判断是否终止
temp_result = s[i:j+1]
if result =='' or len(result) > len(temp_result):
result = temp_result
if window_count[s[i]] == target_count[s[i]]: ## 左边界停止移动条件
break
window_count[s[i]]-=1
i+=1
continue
return result
0077. 组合【中等】
class Solution:
def __init__(self):
self.path = []
self.result = []
def backtracking(self, n, k, start_idx):
if len(self.path) == k:
self.result.append(self.path.copy()) ## .copy()
return
for i in range(start_idx, n+1):
self.path.append(i)
self.backtracking(n, k, i+1)
self.path.pop(-1)
def combine(self, n: int, k: int) -> List[List[int]]:
self.backtracking(n, k, 1)
return self.result
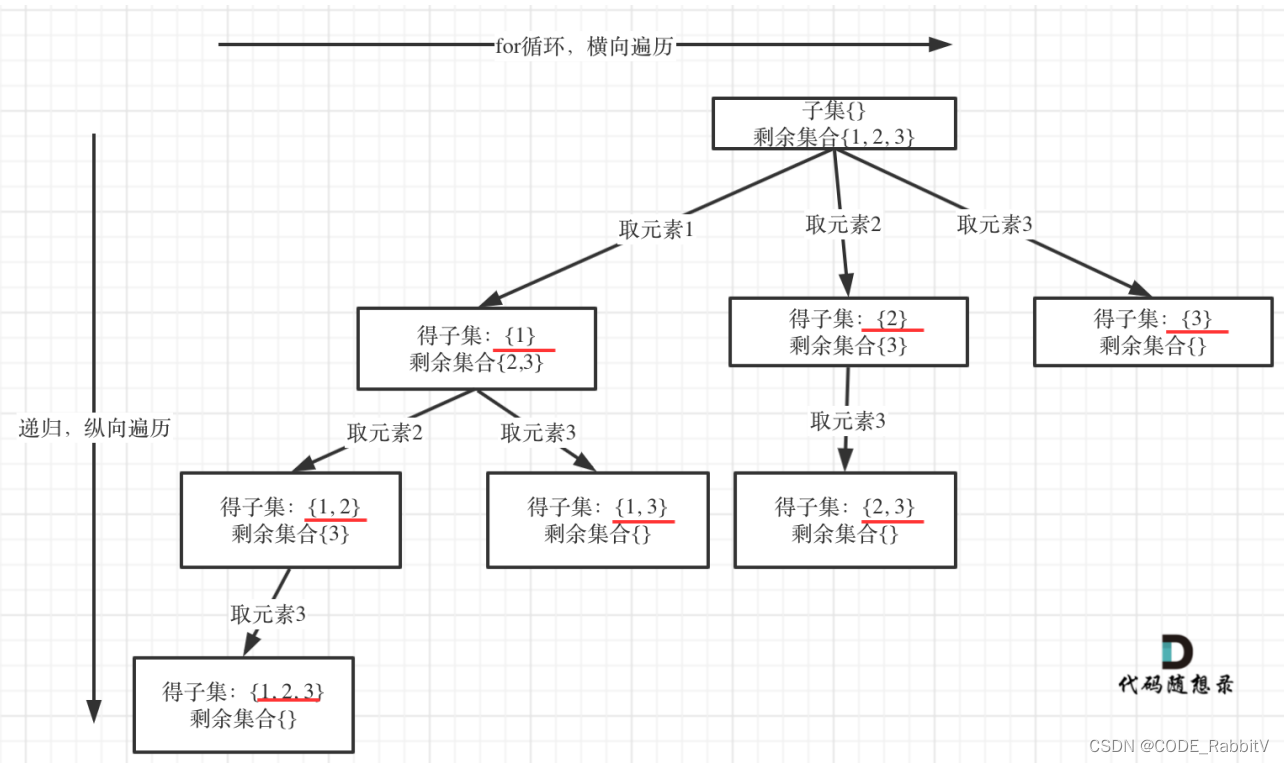
0078. 子集【中等】
如果把 ⼦集问题、组合问题、分割问题都抽象为⼀棵树的话,那么组合问题和分割问题都是收集树的叶⼦节点,⽽⼦集问题是找树的所有节点!
class Solution:
def __init__(self):
self.path = []
self.result = []
def backtracking(self, candidates, start_idx):
self.result.append(self.path.copy()) # 每次都加入,而不是只加入叶子
for i_idx, i in enumerate(candidates[start_idx: ]):
self.path.append(candidates[start_idx+i_idx])
self.backtracking(candidates, i_idx+start_idx+1)
self.path.pop(-1)
def subsets(self, nums: List[int]) -> List[List[int]]:
self.backtracking(nums, 0)
return self.result
0088. 合并两个有序数组【简单】
考察双指针法
class Solution:
def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:
"""
Do not return anything, modify nums1 in-place instead.
"""
mm = 0
nn = 0
result = []
while mm < m and nn < n:
if nums1[mm] <= nums2[nn]:
result.append(nums1[mm])
mm += 1
else:
result.append(nums2[nn])
nn += 1
if mm < m:
result += nums1[mm:]
if nn < n:
result += nums2[nn:]
for _ in range(len(nums1)):
nums1[_] = result[_]
0090. 子集II【中等】
在 No.0078 的基础上,类似 No. 0040 中的去重思路
class Solution:
def __init__(self):
self.path = []
self.result = []
self.used = [] ## 去重
def backtracking(self, candidates, start_idx):
self.result.append(self.path.copy()) # 每次都加入,而不是只加入叶子
for i_idx, i in enumerate(candidates[start_idx: ]):
if i_idx > 0 and candidates[start_idx+i_idx] == candidates[start_idx+i_idx-1] and not self.used[start_idx+i_idx-1]: ## 去重
continue
self.path.append(candidates[start_idx+i_idx])
self.used[i_idx+start_idx] = True
self.backtracking(candidates, i_idx+start_idx+1)
self.path.pop(-1)
self.used[i_idx+start_idx] = False
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
nums.sort() ## 去重
self.used = [False]*len(nums) ## 去重
self.backtracking(nums, 0)
return self.result
0093. 复原 IP 地址
class Solution:
def __init__(self):
self.path = []
self.result = []
self.current_sum = 0
def isPalindrome(self, ss): # 判断回文
if not ss:
return False
for sss in ss:
if not 0 <= eval(sss) <= 9:
return False
if len(ss) > 4:
return False
if len(ss) > 1 and ss[0] == '0':
return False
if eval(ss) > 255:
return False
return True
def backtracking(self, candidates, start_idx):
if len(self.path) >= 3: ## 剪枝
if self.isPalindrome(candidates[start_idx:]): ## 判断最后一段,这个是与其他相关题目不同的,因为是必须四段
temp=self.path.copy()
temp.append(candidates[start_idx:])
self.result.append('.'.join(temp)) ## .copy()
return
for i_idx, i in enumerate(candidates[start_idx: ]):
if self.isPalindrome(candidates[start_idx:start_idx+i_idx+1]): # 子串获取与合法判断
self.path.append(candidates[start_idx:start_idx+i_idx+1])
else:
continue
self.backtracking(candidates, i_idx+start_idx+1)
self.path.pop(-1)
def restoreIpAddresses(self, s: str) -> List[str]:
self.backtracking(s, 0)
return self.result
0094. 二叉树的中序遍历【简单】
同 No. 0144, 单层递归逻辑略有不同
traversal(cur.left, result)
result.append(cur.val)
traversal(cur.right, result)
0096. 不同的二叉搜索树【中等】
0098. 验证二叉搜索树【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def traversal(current_node):
if not current_node: return True, 0, 0
if current_node.left == None and current_node.right == None:
return True, current_node.val, current_node.val
current_min = current_node.val
current_max = current_node.val
if current_node.left:
result, l_min, l_max = traversal(current_node.left)
current_min = min(current_min, l_min)
current_max = max(current_max, l_max)
if not result or current_node.val <= l_max:
return False, 0, 0
if current_node.right:
result, r_min, r_max = traversal(current_node.right)
current_min = min(current_min, r_min)
current_max = max(current_max, r_max)
if not result or current_node.val >= r_min:
return False, 0, 0
return True, current_min, current_max
return traversal(root)[0]
0100. 相同的树【简单】
同 No. 0101, 只是不是比较镜像位置,而是比较相同位置
ll = compare(l.left, r.left)
rr = compare(l.right, r.right)
return (ll and rr)
0101. 对称二叉树【简单】
# 思路一: 根据层级遍历逐层考察是否为对称
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
my_que = deque()
if root: my_que.append(root)
while my_que:
size = len(my_que)
temp = []
for _ in range(size):
current = my_que[0]
my_que.popleft()
if current:
temp.append(current.val)
my_que.append(current.left)
my_que.append(current.right)
else:
temp.append(None)
for _ in range(size//2):
if not temp[_] == temp[-(_+1)]:
return False
return True
# 思路二: 后序处理(因为需要把孩子信息返回上一层),递归法,比较对应位置的值
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
def compare(l, r):
if not l and r:
return False
elif not r and l:
return False
elif not l and not r:
return True
elif not l.val == r.val:
return False
else:
outside = compare(l.left, r.right)
inside = compare(l.right, r.left)
return outside and inside ## 相当于中,所以说是后序
return compare(root.left, root.right)
0102. 二叉树的层序遍历【中等】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
myque = deque()
if root: myque.append(root)
result = []
while myque:
size = len(myque)
temp = []
for _ in range(size): # 每层需要处理的结点数量
current = myque[0] # 1. 获取
myque.popleft() # 2. 弹出
temp.append(current.val)
if current.left: myque.append(current.left) # 3.1 处理后续左
if current.right: myque.append(current.right) # 3.2 处理后续右
result.append(temp)
return result
0104. 二叉树的最大深度【简单】
同 No. 0102, 只需要 result += 1 不需要收集 temp;或者使用如下递归法(后序)
class Solution:
def maxDepth(self, root: Optional[TreeNode]) -> int:
def get_height(node):
if not node: # 终止条件
return 0
l_height = get_height(node.left)
r_height = get_height(node.right)
return max(l_height, r_height) + 1
return get_height(root)
0105. 从前序与中序遍历序列构造二叉树【中等】
同 No. 0106, 只是切割新的前序和中序的方式会不同
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> Optional[TreeNode]:
def traversal(current_preorder, current_inorder):
if not current_preorder:
return None
m_val = current_preorder[0]
new_node = TreeNode(m_val)
if len(current_preorder) == 1:
return new_node
current_preorder = current_preorder[1:]
m_idx = current_inorder.index(m_val)
l_inorder = current_inorder[:m_idx]
r_inorder = current_inorder[m_idx+1:]
l_preorder = current_preorder[:len(l_inorder)]
r_preorder = current_preorder[len(l_inorder):]
new_node.left = traversal(l_preorder, l_inorder)
new_node.right = traversal(r_preorder, r_inorder)
return new_node
return traversal(preorder, inorder)
0106. 从中序与后序遍历序列构造二叉树【中等】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
def traversal(current_inorder, current_postorder):
if not current_postorder:
return None
m_val = current_postorder[-1]
new_node = TreeNode(m_val)
if len(current_postorder) == 1:
return new_node
current_postorder.pop()
m_idx = current_inorder.index(m_val)
l_inorder = current_inorder[:m_idx]
r_inorder = current_inorder[m_idx+1:]
l_postorder = current_postorder[:len(l_inorder)]
r_postorder = current_postorder[len(l_inorder):]
new_node.left = traversal(l_inorder, l_postorder)
new_node.right = traversal(r_inorder, r_postorder)
return new_node
return traversal(inorder, postorder)
0107. 二叉树的层序遍历 II【中等】
同 No. 0102, 只需要最后 result 逆序
0108. 将有序数组转化为二叉搜索树【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
def traversal(left, right):
if left > right: return None
node_idx = (left+right)//2
new_node = TreeNode(nums[node_idx])
new_node.left = traversal(left, node_idx-1)
new_node.right = traversal(node_idx+1, right)
return new_node
return traversal(0, len(nums)-1)
0110. 平衡二叉树【简单】
后序递归求解,关键在于:不平衡则返回高度为 -1
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
def get_height_and_compare(node):
if not node: return 0
l_height = get_height_and_compare(node.left)
r_height = get_height_and_compare(node.right)
is_balance = l_height != -1 and r_height != -1 and abs(l_height - r_height) <= 1
return max(l_height, r_height) + 1 if is_balance else -1
return get_height_and_compare(root) != -1
0111. 二叉树的最小深度【简单】
同 No. 0102, 只需要在发现叶子节点时返回结果
if not current.left and not current.right:
return result + 1
或者同 No. 0104, 采用递归法(后序),但是比求最大深度,多了两行逻辑
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minDepth(self, root: Optional[TreeNode]) -> int:
def get_height(node):
if not node: # 终止条件
return 0
# 多了 这两行逻辑 处理子节点缺失的情况
if not node.left: return get_height(node.right) + 1
if not node.right: return get_height(node.left) + 1
l_height = get_height(node.left)
r_height = get_height(node.right)
return min(l_height, r_height) + 1
return get_height(root)
0112. 路径总和【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
def traversal(node, count):
if node.left == None and node.right == None and count == 0:
return True
if node.left == None and node.right == None and count != 0:
return False
if node.left:
count -= node.left.val
if traversal(node.left, count): return True
count += node.left.val
if node.right:
count -= node.right.val
if traversal(node.right, count): return True
count += node.right.val
return False
if not root:
return False
return traversal(root, targetSum-root.val)
0113. 路径总和 II
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
def traversal(node, count, result, path):
if node.left == None and node.right == None and count == 0:
result.append(path[:]) ## 特别注意这里要用 [:]
return
if node.left == None and node.right == None and count != 0:
return
if node.left:
path.append(node.left.val)
count -= node.left.val
traversal(node.left, count, result, path)
count += node.left.val
path.pop()
if node.right:
path.append(node.right.val)
count -= node.right.val
traversal(node.right, count, result, path)
count += node.right.val
path.pop()
return
if not root:
return []
result = []
path = [root.val]
traversal(root, targetSum-root.val, result, path)
return result
0116. 填充每个节点的下一个右侧指针【中等】
同 No. 0102,只需要顺次连接每层 temp
for i in range(size-1):
temp[i].next = temp[i+1]
0117. 填充每个节点的下一个右侧指针 II【中等】
同 No. 0116, 完全一样
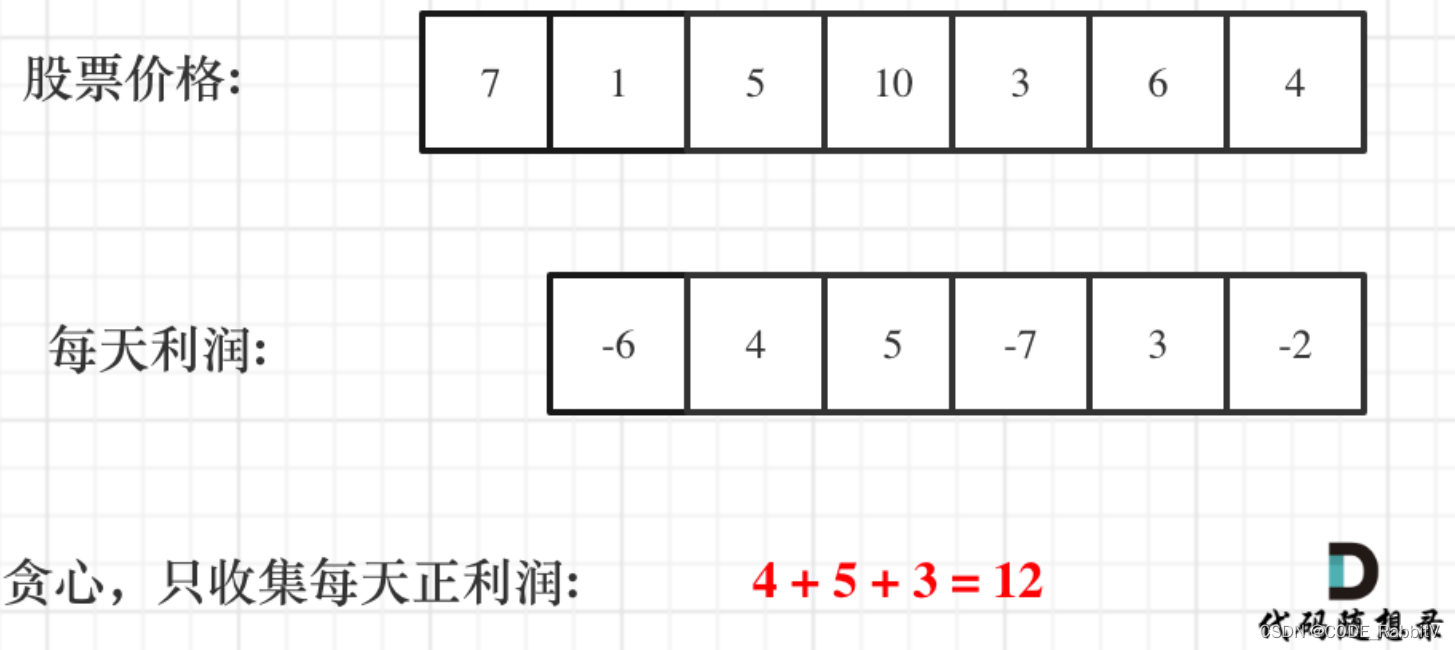
0122. 买卖股票的最佳时机【中等】
class Solution:
def maxProfit(self, prices: List[int]) -> int:
result = 0
for p_idx, p in enumerate(prices):
if p_idx == 0: continue
result += max(p-prices[p_idx-1], 0)
return result
0121. 买卖股票的最佳时机1【简单】
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) == 0: return 0
# dp[i][0] 表示 第 i 天 持有股票所得最多现金
# dp[i][1] 表示 第 i 天 不持有股票所得最多现金
# 如果第 i 天持有股票
## 如果第 i-1 天已持有股票:dp[i][0] = dp[i-1][0]
## 如果第 i 天才买入:dp[i][0] = -prices[i]
# 如果第 i 天不持有股票
## 如果第 i-1 天已卖出股票:dp[i][1] = dp[i-1][1]
## 如果第 i 天才卖出:dp[i][1] = prices[i]-dp[i-1][0]
dp = [[-prices[0],0] for i in range(len(prices))]
for i in range(1,len(prices)):
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1], prices[i]+dp[i-1][0])
return dp[-1][1]
0122. 买卖股票的最佳时机 II 【中等】
区别在于虽然当前仍是最多可持有一个股票,但是可以多次买卖
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) == 0: return 0
# dp[i][0] 表示 第 i 天 持有股票所得最多现金
# dp[i][1] 表示 第 i 天 不持有股票所得最多现金
# 如果第 i 天持有股票
## 如果第 i-1 天已持有股票(第 i 天不买入):dp[i][0] = dp[i-1][0]
## 如果第 i 天才买入:dp[i][0] = -prices[i] + dp[i-1][1] # *** 区别点在于此
# 如果第 i 天不持有股票
## 如果第 i-1 天已卖出股票:dp[i][1] = dp[i-1][1]
## 如果第 i 天才卖出:dp[i][1] = prices[i]-dp[i-1][0]
dp = [[-prices[0],0] for i in range(len(prices))]
for i in range(1,len(prices)):
dp[i][0] = max(dp[i-1][0], -prices[i]+ dp[i-1][1]) # *** 区别点在于此
dp[i][1] = max(dp[i-1][1], prices[i]+dp[i-1][0])
return dp[-1][1]
0122. 路径加密 (LCR)【简单】
字符串替换
class Solution:
def pathEncryption(self, path: str) -> str:
result = []
for _ in path:
if _ == '.':
result.append(' ')
else:
result.append(_)
return ''.join(result)
0123. 买卖股票的最佳时机 III 【中等】
与 0121 和 0122 的区别在于最多进行两次交易,故设置 dp 数组时区分是第一次(不)持有还是第二次(不)持有
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) == 0: return 0
# dp[i][0] 表示 第 i 天 第一次持有股票所得最多现金
# dp[i][1] 表示 第 i 天 第一次不持有股票所得最多现金
# dp[i][2] 表示 第 i 天 第二次持有股票所得最多现金
# dp[i][3] 表示 第 i 天 第二次不持有股票所得最多现金
# 如果第 i 天持有股票
# 第一次 - - - - - -
## 如果第 i-1 天已持有股票:dp[i][0] = dp[i-1][0] -> 延续
## 如果第 i 天才买入:dp[i][0] = -prices[i]
# 第二次 - - - - - -
## 如果第 i-1 天已持有股票:dp[i][2] = dp[i-1][2] -> 延续
## 如果第 i 天才买入:dp[i][2] = -prices[i] + dp[i-1][1]
# 如果第 i 天不持有股票
# 第一次 - - - - - -
## 如果第 i-1 天已卖出股票:dp[i][1] = dp[i-1][1] -> 延续
## 如果第 i 天才卖出:dp[i][1] = prices[i]+dp[i-1][0]
# 第二次 - - - - - -
## 如果第 i-1 天已卖出股票:dp[i][3] = dp[i-1][3] -> 延续
## 如果第 i 天才卖出:dp[i][3] = prices[i]+dp[i-1][2]
dp = [[-prices[0],0, -prices[0],0] for i in range(len(prices))]
for i in range(1,len(prices)):
dp[i][0] = max(dp[i-1][0], -prices[i])
dp[i][1] = max(dp[i-1][1], prices[i]+dp[i-1][0])
dp[i][2] = max(dp[i-1][2], -prices[i]+ dp[i-1][1])
dp[i][3] = max(dp[i-1][3], prices[i]+dp[i-1][2])
return dp[-1][-1]
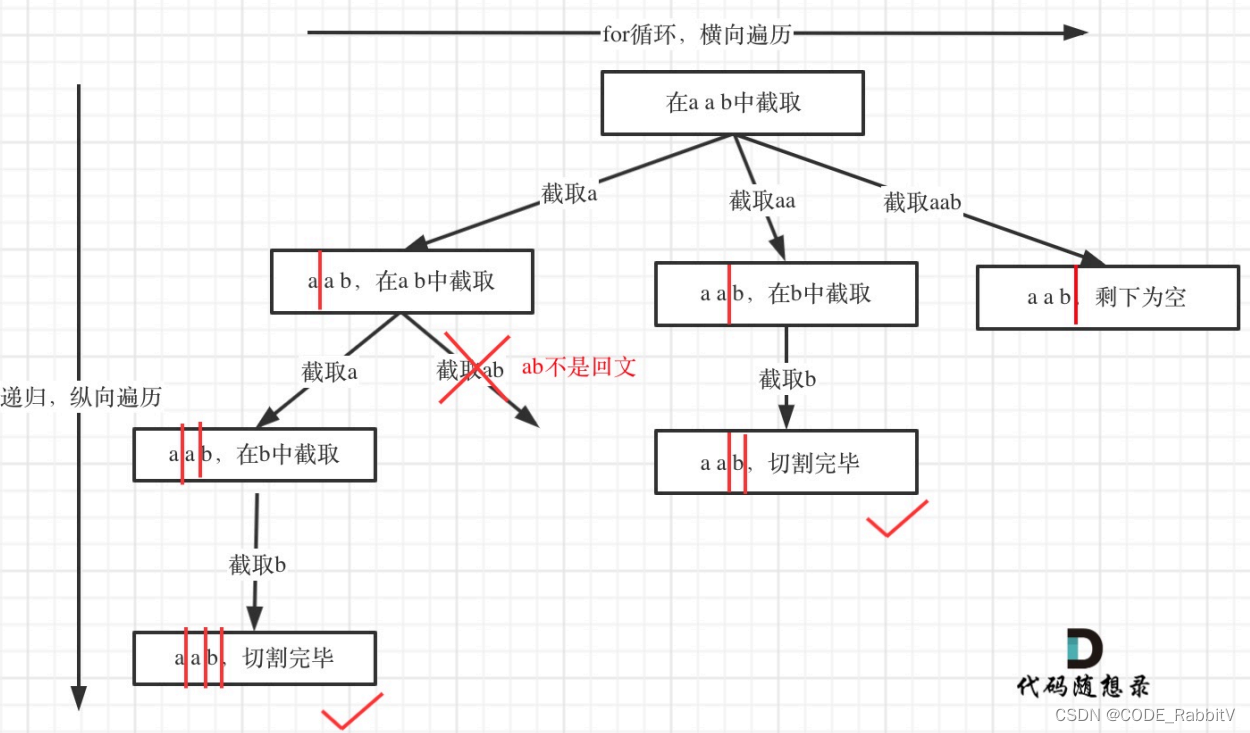
0131. 分割回文串【中等】
class Solution:
def __init__(self):
self.path = []
self.result = []
self.current_sum = 0
def isPalindrome(self, ss): # 判断回文
i = 0
j = len(ss)-1
while i<j:
if ss[i] != ss[j]:
return False
i += 1
j -= 1
return True
def backtracking(self, candidates, start_idx):
if start_idx >= len(candidates): ## 剪枝
self.result.append(self.path.copy()) ## .copy()
return
for i_idx, i in enumerate(candidates[start_idx: ]):
if self.isPalindrome(candidates[start_idx:start_idx+i_idx+1]): # 子串获取与回文判断
self.path.append(candidates[start_idx:start_idx+i_idx+1])
else:
continue
self.backtracking(candidates, i_idx+start_idx+1)
self.path.pop(-1)
def partition(self, s: str) -> List[List[str]]:
self.backtracking(s, 0)
return self.result
0134. 加油站【中等】
class Solution:
def canCompleteCircuit(self, gas: List[int], cost: List[int]) -> int:
start = 0
total = 0
temp = 0
for _ in range(len(gas)):
total += gas[_] - cost[_]
temp += gas[_] - cost[_]
if temp < 0:
start = _ + 1
temp = 0
return start if total >= 0 else -1
0135. 分发糖果【困难】
难点在于 如何想到利用贪心算法求解
class Solution:
def candy(self, ratings: List[int]) -> int:
# 左规则 ->
candy = [1]
for i_idx in range(1, len(ratings)):
candy.append(candy[i_idx-1]+1 if ratings[i_idx] > ratings[i_idx-1] else 1)
# 右规则 <-
for i_idx in range(len(ratings)-2,-1,-1):
temp = candy[i_idx+1]+1 if ratings[i_idx] > ratings[i_idx+1] else 1
candy[i_idx] = max(candy[i_idx], temp)
# 为什么取最大值是正确的思考:
# 如果 A > B ,则按照左规则处理后,B不会比A多;按照右规则处理后,A一定比B多,那么A一定会被更新(变大),但L、R规则仍然成立:B不会比A多,A一定比B多;
# 同理可讨论 A<B;
# 当 A == B,A、B的值无论如何更新,都不影响 L、R规则
return sum(candy)
0139. 单词拆分【中等】
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
dp = [False] * (len(s)+1)
dp[0] = True
for i in range(1, len(s)+1): ## 遍历背包
for j in range(i): # 没有要 i+1 -> 会截取到空串
word = s[j:i] # 截取物品
if word in wordDict and dp[j]:
dp[i] = True # 长度为 i 的字符串可以被合理拆分
break
return dp[-1]
0142. 环形链表 II【中等】
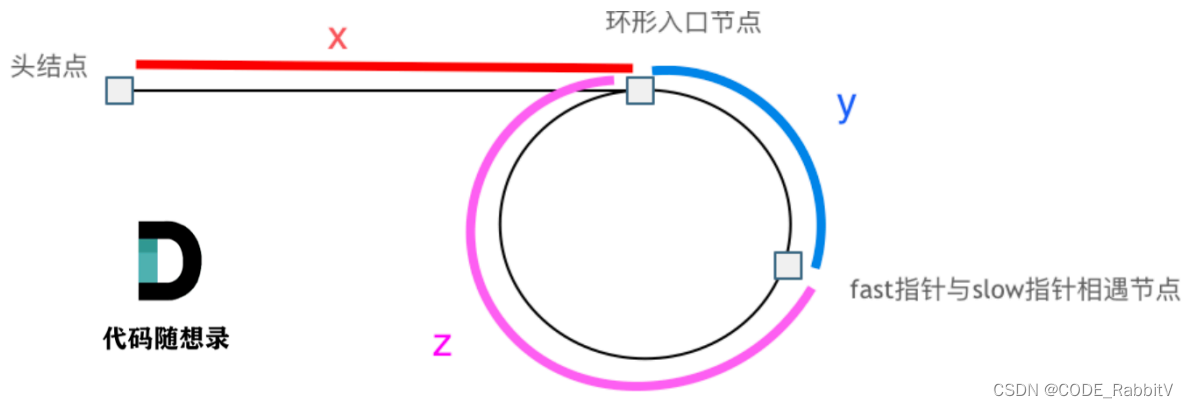
- 判断链表是否环:步长为1的
slow和步长为2的fast相遇,则可判定有环 - 如果有环,如何找到这个环的入口:可推导出如下关系:
x = (n - 1) (y + z) + z, 所以找环入口的话应该 让两个相同步长的指针分别从头结点、fast指针与slow节点相遇节点
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: Optional[ListNode]) -> Optional[ListNode]:
slow = head
fast = head
while slow and fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast: ## 快慢相遇,环判定成功,开始找环入口
temp = head
while not slow == temp:
slow = slow.next
temp = temp.next
return slow
return None
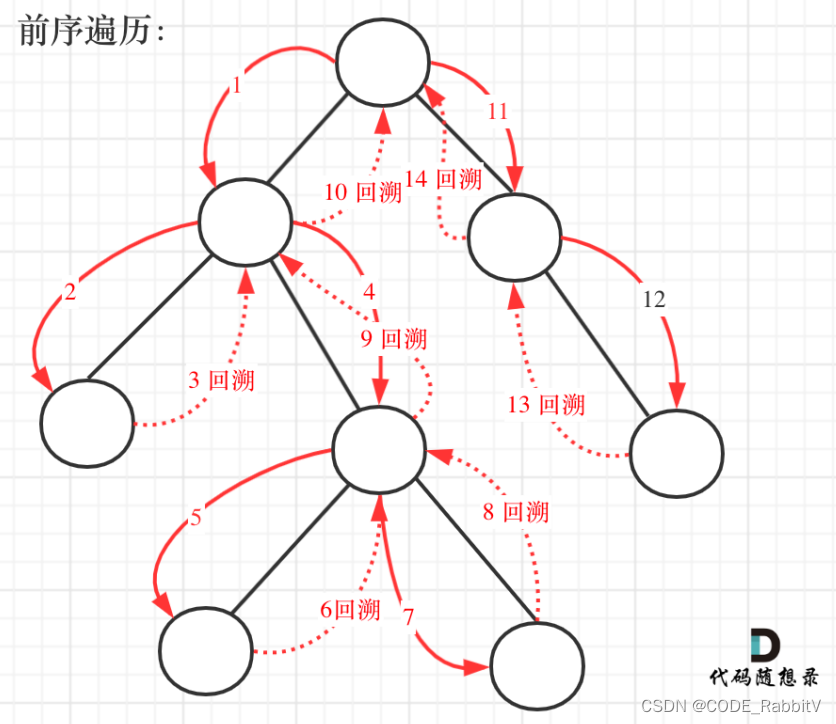
0144. 二叉树的前序遍历【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
def traversal(cur, result):
if not cur:
return
result.append(cur.val)
traversal(cur.left, result)
traversal(cur.right, result)
result = []
traversal(root, result)
return result
0145. 二叉树的后序遍历【简单】
同 No. 0144, 单层递归逻辑略有不同
traversal(cur.left, result)
traversal(cur.right, result)
result.append(cur.val)
0150. 逆波兰表达式求值【中等】
同 No.0020, 考察栈操作
class Solution:
def evalRPN(self, tokens: List[str]) -> int:
result = []
for ss in tokens:
if ss in ['+', '-', '*', '/']:
num2 = result.pop()
num1 = result.pop()
result.append(str(int(eval(num1+ss+num2))))
else:
result.append(ss)
return eval(result[0])
0151. Reverse Word in a String【中等】
可以使用库函数 " ".join(reversed(s.split())) 直接解决或者:
class Solution:
def reverseWords(self, s: str) -> str:
result = [] # 存储翻转后的单词
i = 0 # 当前单词的起始位置
j = len(s) # 当前单词的结束位置(初始为字符串的长度)
while True:
if i >= len(s): # 如果已经遍历完整个字符串,结束循环
break
if s[i] == ' ': # 如果当前字符是空格,跳过该字符,继续查找下一个字符
i += 1
continue
j = i # 找到当前单词的起始位置 i,开始寻找单词的结束位置 j
while j < len(s) and not s[j] == ' ': # 当 j 未越界且当前字符不是空格时,继续向后寻找
j += 1
result = [s[i:j]] + result # 将当前单词添加到结果列表的头部(实现翻转)
i = j + 1 # 更新 i,开始查找下一个单词
return ' '.join(result) # 将结果列表中的单词用空格连接起来,并返回最终结果
0160. 相交链表【简单】
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> Optional[ListNode]:
def get_len(list_head):
current_node = list_head
l = 0
while current_node:
l += 1
current_node = current_node.next
return l
A_len = get_len(headA)
B_len = get_len(headB)
current_node_A = headA
current_node_B = headB
if A_len > B_len:
l_move = A_len - B_len
while l_move:
current_node_A = current_node_A.next
l_move -= 1
if B_len > A_len:
l_move = B_len - A_len
while l_move:
current_node_B = current_node_B.next
l_move -= 1
# 以上移动到了尾端对其得位置,开始移动比较
while current_node_A and current_node_B and not current_node_A == current_node_B:
current_node_A = current_node_A.next
current_node_B = current_node_B.next
return current_node_A
0188. 买卖股票的最佳时机 IV 【困难】
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if len(prices) == 0: return 0
# dp[i][2*k-1] 表示 第 i 天 第k次持有股票所得最多现金
# dp[i][2*k] 表示 第 i 天 第k次不持有股票所得最多现金
# 如果第 i 天持有股票
# 第k次 - - - - - -
## 如果第 i-1 天已持有股票:dp[i][2*j-1] = dp[i-1][2*j-1] -> 延续
## 如果第 i 天才买入:dp[i][2*j-1] = -prices[i] + dp[i-1][2*j-2]
# 如果第 i 天不持有股票
# 第k次 - - - - - -
## 如果第 i-1 天已卖出股票:dp[i][2*j] = dp[i-1][2*j] -> 延续
## 如果第 i 天才卖出:dp[i][2*j] = prices[i]+dp[i-1][2*j-1]
dp = [[0 for j in range(2*k+1)] for i in range(len(prices))]
for j in range(1, k+1): ## 注意初始化
dp[0][2*j-1] = -prices[0]
for i in range(1,len(prices)):
for j in range(1, k+1): ## 根据两次交易找规律获得
dp[i][2*j-1] = max(dp[i-1][2*j-1], -prices[i]+ dp[i-1][2*j-2])
dp[i][2*j] = max(dp[i-1][2*j], prices[i]+dp[i-1][2*j-1])
return dp[-1][-1]
0199. 二叉树的右视图【中等】
同 No.0102, 但是每层只需加入最后一个值 result.append(temp[-1])
0202. 快乐数【简单】
难点一:题⽬中说了会 ⽆限循环,那么也就是说求和的过程中,sum会重复出现,这对解题很重要!
难点二:求和的过程: 考察对取数值各个位上的单数操作
class Solution:
def isHappy(self, n: int) -> bool:
def get_sum(n): # 难点二
sum = 0
while n:
nn = (n%10)**2
sum += nn
n //= 10
return sum
result_sum = set()
while True:
n = get_sum(n)
if n == 1:
return True
if n in result_sum: # 难点一
return False
result_sum.add(n)
0203. Remove Linked List Elements【简单】
考察链表删除,建立虚拟头节点更方便操作
class Solution:
def removeElements(self, head: Optional[ListNode], val: int) -> Optional[ListNode]:
current_node = dummy_node = ListNode(val=-1, next=head)
while current_node.next:
if current_node.next.val == val:
current_node.next = current_node.next.next
else: #### 一定要注意这个 else 不是每一次都往后移动,不发生删除才移动
current_node = current_node.next
return dummy_node.next
0206. Reverse Linked List【简单】
考察链表基本操作,同203
# 方法一: 不断在头部插入
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
dumy_head = ListNode()
current_node = head
while current_node:
new_node = ListNode(current_node.val, dumy_head.next)
dumy_head.next = new_node
current_node = current_node.next
return dumy_head.next
# 方法二: 直接以此改变指向
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
pre = None
cur = head
while cur:
temp = cur.next
cur.next = pre
pre = cur
cur = temp
return pre
# 方法三:方法二的递归写法
class Solution:
def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
def reverse(pre, cur):
if cur == None:
return pre
temp = cur.next
cur.next = pre
return reverse(cur, temp)
return reverse(None, head)
0209. Minimum Size Subarray Sum【中等】
考察滑动窗口法,判断清窗口内是什么,何时移动窗口起始、终止位置
class Solution(object):
def minSubArrayLen(self, target, nums):
i = 0 # 窗口起始位置
j = 0 # 窗口终止位置
current_sum = 0
results = 100001
for j in range(len(nums)): # 遍历
current_sum += nums[j]
while current_sum >= target: # 窗口内是什么
temp = j-i+1
results = results if results < temp else temp
current_sum -= nums[i]
i += 1 # 缩小窗口
return results if not results == 100001 else 0
0213. 打家劫舍 II【中等】
与 No. 0198 的区别在于,目标首尾相连,故按两种情况处理
class Solution:
def rob(self, nums: List[int]) -> int:
def rob198(nums):
if len(nums) == 0: return 0
if len(nums) == 1: return nums[0]
dp = [0] * len(nums)
# 递推公式初始化:
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, len(nums)):
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
return dp[-1]
# 以上为 no.198 代码,下列按两种情况,用 no.198 的思路求解本题
# 情况一:不考虑首元素
# 情况二:不考虑尾元素
if len(nums) == 0: return 0
if len(nums) == 1: return nums[0]
return max(rob198(nums[1:]), rob198(nums[:-1]))
0216. 组合总和 III【中等】
class Solution:
def __init__(self):
self.path = []
self.result = []
self.current_sum = 0
def backtracking(self, n, k, start_idx):
if self.current_sum > n: ## 剪枝
return
if len(self.path) == k:
if self.current_sum == n:
self.result.append(self.path.copy()) ## .copy()
return
for i in range(start_idx, 10):
self.path.append(i)
self.current_sum += i
self.backtracking(n, k, i+1)
self.path.pop(-1)
self.current_sum -= i
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
self.backtracking(n, k, 1)
return self.result
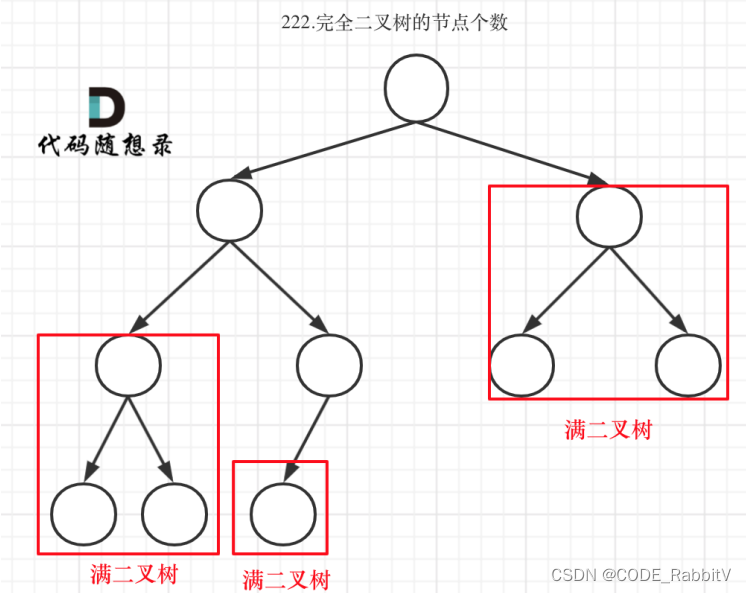
0222. 完全二叉树的节点个数【简单】
可以把完全二叉树当作一般二叉树,采取任何一种遍历方式计数 (O(n));或者利用完全二叉树的特点 (O(log(n))): 找到满二叉树子树(左外侧和右外侧深度相等),往上返回
如果节点是满二叉树,直接按 2**height - 1 返回深度;否则按左+右+1返回
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def countNodes(self, root: Optional[TreeNode]) -> int:
def get_side_height(node, d='_'):
if not node: return 0
if d == 'l': return get_side_height(node.left, 'l') + 1
if d == 'r': return get_side_height(node.right, 'r') + 1
def get_nums(node):
if not node: return 0
ll = get_side_height(node.left, 'l')
rr = get_side_height(node.right, 'r')
if ll == rr: # 是满的
return 2**(ll+1) - 1
else:
return get_nums(node.left) + get_nums(node.right) + 1
return get_nums(root)
0225. Implement Stack Using Queues【简单】
class MyStack:
def __init__(self):
self.que = deque()
def push(self, x: int) -> None:
self.que.append(x)
def pop(self) -> int: # 重点在于 pop
if self.empty():
return None
for i in range(len(self.que)-1):
self.que.append(self.que.popleft())
return self.que.popleft()
def top(self) -> int:
temp = self.pop()
self.que.append(temp)
return temp
def empty(self) -> bool:
return not self.que
# Your MyStack object will be instantiated and called as such:
# obj = MyStack()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.top()
# param_4 = obj.empty()
0226. 翻转二叉树【简单】
同 No. 0102, 但是不需要分层统计 temp;只需要按照层级顺序处理每个节点,交换其左右孩子节点
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
my_que = deque()
if root: my_que.append(root)
while my_que:
current = my_que[0]
if current.left: my_que.append(current.left)
if current.right: my_que.append(current.right)
## 交换
temp = current.left
current.left = current.right
current.right = temp
my_que.popleft()
return root
0232. 用栈实现队列【简单】
用两个栈 stack_in 和 stack_out 实现队列
class MyQueue:
def __init__(self):
self.stack_in = []
self.stack_out = []
def push(self, x: int) -> None:
self.stack_in.append(x)
def pop(self) -> int: # 重点在于 pop
if not self.stack_out:
for i in range(len(self.stack_in)):
self.stack_out.append(self.stack_in.pop())
return self.stack_out.pop()
def peek(self) -> int:
ans = self.pop()
self.stack_out.append(ans)
return ans
def empty(self) -> bool:
return not (self.stack_in or self.stack_out)
# Your MyQueue object will be instantiated and called as such:
# obj = MyQueue()
# obj.push(x)
# param_2 = obj.pop()
# param_3 = obj.peek()
# param_4 = obj.empty()
0235. 二叉搜索树的最近公共祖先【中等】
因为是有序树,所有 如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 ⼀定是在 [p, q]区间的。即 中节点 >
p && 中节点 < q 或者 中节点 > q && 中节点 < p。否则 砍掉一半树找。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
def traversal(node):
if not node:
return None
if node.val > p.val and node.val > q.val:
left = traversal(node.left)
if left: return left
if node.val < p.val and node.val < q.val:
right = traversal(node.right)
if right: return right
return node
return traversal(root) ## 在 pq 中间, 找到
0236. 二叉树的最近公共祖先【中等】
如果(后序)递归遍历遇到q,就将q返回,遇到p 就将p返回,那么如果左右⼦树的返回值都不为空,说明此时的中节点,⼀定是 q 和 p 的最近祖先
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
def traversal(node):
if not node or node == p or node == q:
return node
result_l = traversal(node.left)
result_r = traversal(node.right)
if result_l and result_r:
return node # 此时的中节点,⼀定是 q 和 p 的最近祖先
if not result_l and result_r:
return result_r
if result_l and not result_r:
return result_l
return None
return traversal(root)
0239. 滑动窗口最大值【困难】
通过维护一个特殊的有序队列 Myque 实现
class MyQueue: # 队列按降序排列
def __init__(self):
self.que = deque()
def pop(self, val):
if self.que and val == self.front(): # val 非最大值的情况已经在 push 被移走了
self.que.popleft()
def push(self, val): # 把无效值(比当前val小的)都挤走
while self.que and val > self.que[-1]:
self.que.pop()
self.que.append(val)
def front(self): # 维护当前队列最大值
return self.que[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
q = MyQueue()
for _ in range(k):
q.push(nums[_])
result = [q.front()]
for end_idx in range(k, len(nums)):
q.pop(nums[end_idx-k])
q.push(nums[end_idx])
result.append(q.front())
return result
0242. 有效的字母异位词【简单】
考察哈希表,用哈希表存储统计结果,可以只用一个表,对于s加入,对于t删除
class Solution:
def isAnagram(self, s: str, t: str) -> bool:
check = {}
for _ in s: # 对于`s`加入
if _ in check.keys():
check[_] += 1
else:
check[_] = 1
for _ in t: # 对于`t`删除
if _ in check.keys():
check[_] -= 1
if check[_] == 0:
check.pop(_)
else:
return False
0257. 二叉树的所有路径【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
def traversal(node, path, result):
path.append(node.val)
if node.left == None and node.right == None:
result.append('->'.join(str(x) for x in path))
return
if node.left:
traversal(node.left, path, result) ## 递归
path.pop() # 回溯
if node.right:
traversal(node.right, path, result)
path.pop()
result = []
traversal(root, [], result)
return result
0279. 完全平方数【中等】
class Solution:
def numSquares(self, n: int) -> int:
dp = [100]*(n+1) ## 难点在于要初始化为很大的值避免被初值覆盖
dp[0] = 0
for i in range(n+1): ## 遍历物品
for j in range(i*i, n+1): ## 遍历容量 倒序保证每个物品只被添加一次
dp[j] = min(dp[j], dp[j-i*i]+1)
return dp[-1]
0283. Move Zeroes【简单】
考察双指针法,同 0027,只是需要将后续空余位置补 0
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
slow = 0 ## 一般双指针
for fast in range(len(nums)):
if not nums[fast] == 0:
nums[slow] = nums[fast]
slow += 1
while slow < len(nums): ## 补 0
nums[slow] = 0
slow += 1
0300. 最长递增子序列【中等】
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
# dp[i]: 【 以 num[i] 为结尾的 】最长递增子序列长度
# dp[i]: 初始化为1(至少包含 nums[i])
### num[i] > num[j]: max(dp[i],dp[j]+1)
### num[i] <= num[j]
dp = [1 for _ in range(len(nums))]
for i in range(1, len(nums)):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i],dp[j]+1)
return max(dp)
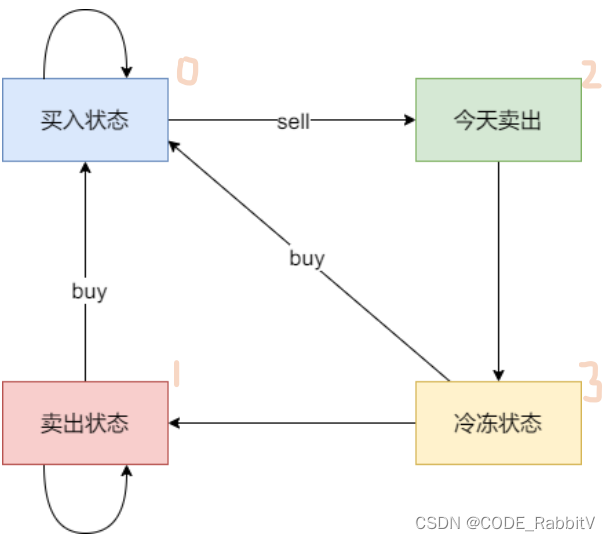
0309. 买卖股票的最佳时机韩冷冻期【中等】
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) == 0: return 0
# 根据状态转移图理解当前状态由前一天的哪些状态获得
# dp[i][0] 表示 第 i 天 持有股票所得最多现金
## 如果第 i-1 天已持有股票(第 i 天不买入):dp[i][0] = dp[i-1][0]
## 如果第 i 天才买入
### 如果前一天是卖出 dp[i][0] = -prices[i] + dp[i-1][1]
### 如果前一天是冷冻 dp[i][0] = -prices[i] + dp[i-1][3]
# dp[i][1] 表示 第 i 天 保持卖出所得最多现金
## 如果前一天是卖出 dp[i-1][1]
## 如果前一天是冷冻 dp[i-1][3]
# dp[i][2] 表示 第 i 天 今天卖出所得最多现金
## dp[i-1][0] + price[i]
# dp[i][3] 表示 第 i 天 今天冷冻所得最多现金
## dp[i-1][2]
dp = [[-prices[0],0,0,0] for i in range(len(prices))]
for i in range(1,len(prices)):
dp[i][0] = max(dp[i-1][0], -prices[i]+ dp[i-1][1], -prices[i]+ dp[i-1][3])
dp[i][1] = max(dp[i-1][1], dp[i-1][3])
dp[i][2] = prices[i]+dp[i-1][0]
dp[i][3] = dp[i-1][2]
return max(dp[-1])
0332. 重新安排行程【困难】
- ⼀个⾏程中,如果航班处理不好容易变成⼀个圈,成为死循环
- 有多种解法,字⺟序靠前排在前⾯,让很多同学望⽽退步,如何该记录映射关系呢 ?
- 使⽤回溯法(也可以说深搜) 的话,那么终⽌条件是什么呢?
- 搜索的过程中,如何遍历⼀个机场所对应的所有机场。
# 回溯算法,会超时
class Solution:
def __init__(self):
self.results = []
self.path = ["JFK"]
def backtracking(self, tickets, cur):
if len(self.path) == len(tickets) + 1: # 终止条件:路径长度等于机票数量+1
self.results.append(self.path[:]) # 将当前路径添加到结果列表
return True
for i, ticket in enumerate(tickets): # 遍历机票列表
if ticket[0] == cur and self.used[i] == 0: # 找到起始机场为cur且未使用过的机票
self.used[i] = 1 # 标记该机票为已使用
self.path.append(ticket[1]) # 将到达机场添加到路径中
if self.backtracking(tickets, ticket[1]): # 递归搜索
return True # 只要找到一个可行路径就返回,不继续搜索
self.path.pop(-1) # 回溯,移除最后添加的到达机场
self.used[i] = 0 # 标记该机票为未使用
def findItinerary(self, tickets: List[List[str]]) -> List[str]:
tickets.sort() # 先排序,这样一旦找到第一个可行路径,一定是字母排序最小的
self.used = [False] * len(tickets)
self.backtracking(tickets, 'JFK')
return self.results[0]
0337. 打家劫舍
树形 dp 入门题目
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
def robTree(cur): # 后序遍历,因为要用到左右孩子的结果
if cur == None:
return [0, 0]
leftdp = robTree(cur.left)
rightdp = robTree(cur.right)
val1 = cur.val + leftdp[1] + rightdp[1] # 偷 cur
val2 = max(leftdp) + max(rightdp) # 不偷 cur
return [val1, val2]
result = robTree(root)
return max(result[0], result[1])
0343. 整数拆分【中等】
class Solution:
def integerBreak(self, n: int) -> int:
dp = [0]*(n+1)
dp[2] = 1
for i in range(3, n+1):
for j in range(1, i-1):
dp[i] = max(dp[i],j*max(i-j, dp[i-j])) ## 难点在于递推公式
return dp[-1]
0344. Reverse String【简单】
对于字符串,我们定义两个指针(也可以说是索引下标),⼀个从字符串前⾯,⼀个从字符串后⾯,两个指针同时向中间移动,并交换元素
class Solution:
def reverseString(self, s: List[str]) -> None:
"""
Do not return anything, modify s in-place instead.
"""
i = 0
j = len(s) - 1
while i<j:
temp = s[i]
s[i] = s[j]
s[j] = temp
i += 1
j -= 1
0347. 前 k 个高频元素【中等】
考察 小顶堆 heapq
class Solution:
def topKFrequent(self, nums: List[int], k: int) -> List[int]:
# 统计频率
result_temp = {}
for _ in nums:
result_temp[_] = result_temp.get(_, 0)+1
# 用小顶堆维护最大的 k 个元素
pri_que = []
import heapq
for kk, vv in result_temp.items():
heapq.heappush(pri_que, (vv,kk))
if len(pri_que) > k:
heapq.heappop(pri_que)
# 输出结果
result = []
for _ in pri_que:
result.append(_[1])
return result
0349. 两个数的交集【简单】
考察哈希表
class Solution:
def intersection(self, nums1: List[int], nums2: List[int]) -> List[int]:
nums1 = set(nums1)
nums2 = set(nums2)
result = []
for _ in nums1:
if _ in nums2:
result.append(_)
return result
0350. 两个数组的交集II【简单】
class Solution:
def intersect(self, nums1: List[int], nums2: List[int]) -> List[int]:
def todict(nums):
result = {}
for _ in nums:
if _ in result.keys():
result[_] += 1
else:
result[_] = 1
return result
# ----- 转化成字典
num1 = todict(nums1)
num2 = todict(nums2)
result = []
for _ in num1.keys():
if _ in num2.keys():
times = min(num1[_], num2[_])
for i in range(times):
result.append(_)
return result
0367. Valid Perfect Square【简单】
考察二分查找,同 0704,先掌握 0704
只是不再返回找到的坐标,而是找到返回 True, 没有找到返回 False
class Solution:
def isPerfectSquare(self, num: int) -> bool:
left, right = 0, num
while left<=right:
middle = left + (right-left)//2
if middle*middle < num:
left = middle + 1
elif middle*middle > num:
right = middle - 1
else:
return True
return False
0376. 摆动序列【中等】
直接贪心算法,重点注意注释的两行
class Solution:
def wiggleMaxLength(self, nums: List[int]) -> int:
last_direction = None
result = 1
for i in range(1, len(nums)):
if nums[i] > nums[i-1]:
new_direction = 1
elif nums[i] < nums[i-1]:
new_direction = -1
else:
new_direction = last_direction if last_direction is not None else 0 ##
if new_direction == 0 or new_direction == last_direction: ##
continue
result += 1
last_direction = new_direction
return result
0377. 组合总和 IV【中等】
同零钱兑换,但是是先遍历背包,后遍历物品
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0]*(target+1)
dp[0] = 1
for j in range(target+1): ## 遍历容量 倒序保证每个物品只被添加一次
for i in range(len(nums)): ## 遍历物品
if j-nums[i] >= 0:
dp[j] += dp[j-nums[i]] ## 难点
return dp[-1]
0383. Ransom Note【简单】
考察哈希表,用 list 代替 map 可以获得更高的效率
## 方法一:采用 map
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
def toDict(l):
result = dict()
for _ in l:
if _ in result.keys():
result[_] += 1
else:
result[_] = 1
return result
r = toDict(ransomNote)
m = toDict(magazine)
for rr in r.keys():
if rr in m.keys():
if r[rr] > m[rr]:
return False
else:
return False
return True
## 方法二:采用 list
class Solution:
def canConstruct(self, ransomNote: str, magazine: str) -> bool:
m = [0] * 26
for mm in magazine:
m[ord(mm) - ord('a')] += 1
for rr in ransomNote:
m[ord(rr)-ord('a')] -= 1
if m[ord(rr)-ord('a')] < 0:
return False
return True
0392 判断子序列
同 1143
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
# 注意:元素之间可以不连续
# ⽤⼆维数组可以记录两个字符串的所有⽐较情况
# dp[i][j]: 以下标 i-1 为结尾的A,和以下标 j-1 为结尾的B,
# 最⻓重复⼦数组⻓度为dp[i][j]
result = 0
dp = [[0 for _ in range(len(t)+1)] for _ in range(len(s)+1)]
for i in range(1, len(s)+1):
for j in range(1, len(t)+1):
if s[i-1] == t[j-1]: ## 递推
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
if dp[i][j] > result: result = dp[i][j]
return result==len(s) ## 同 1143 通过判断长度来判断子序列
0404. 左叶子之和【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
def traversal(node):
if not node: return 0
if not node.left and not node.right: return 0 # 因为无法通过当前节点是不是左孩子
current_sum_L = traversal(node.left) # 左
if node.left and node.left.left == None and node.left.right == None:
current_sum_L = node.left.val # 所以这在里,修改 0 为左孩子的值
current_sum_R = traversal(node.right) # 右
return current_sum_L + current_sum_R # 中
return traversal(root)
0406. 根据身高重建队列【中等】
难点在于如何想到用贪心算法,以及判定有两个维度,以及首先处理哪个维度
class Solution:
def reconstructQueue(self, people: List[List[int]]) -> List[List[int]]:
# 本题有两个维度,h和k,看到这种题⽬⼀定要想如何确定⼀个维度,然后再按照另⼀个维度重新排列
sorted_people = sorted(people, key=lambda x: (-x[0], x[1]))
# 排序后每个人前面的所有人身高一定比他高
# 按照 k 调整
result = []
for pp in sorted_people:
result.insert(pp[1], pp)
return result
0416. 分割等和子集【中等】
class Solution:
def canPartition(self, nums: List[int]) -> bool:
bag_sum = sum(nums)
if bag_sum % 2: return False
target = int(bag_sum // 2)
dp = [0]*(target+1)
for i in range(len(nums)): ## 遍历物品
for j in range(target, nums[i]-1, -1): ## 遍历容量 倒序保证每个物品只被添加一次
dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])
return dp[-1]==target
0429. N叉树的层序遍历【中等】
同 No. 0102, 只是不仅有左右孩子,可能有任意数量的子节点
for c in current.children:
if c: myque.append(c)
0435. 无重叠区间【中等】
类似射爆气球,只需统计重叠区间数
class Solution:
def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
sorted_intervals = sorted(intervals, key=lambda x: x[0])
result = 0
l = sorted_intervals[0][1]
for pp in range(1, len(sorted_intervals)):
if sorted_intervals[pp][0] < l: ## < 根据题意,没有 =
l = min(sorted_intervals[pp][1], l)
result += 1
else:
l = sorted_intervals[pp][1]
return result
0450. 删除二叉搜索树中的节点
把⼆叉搜索树中删除节点遇到的情况都搞清楚。
有以下五种情况:
第⼀种情况:没找到删除的节点,遍历到空节点直接返回了
找到删除的节点
第⼆种情况:左右孩⼦都为空(叶⼦节点),直接删除节点, 返回NULL为根节点
第三种情况:删除节点的左孩⼦为空,右孩⼦不为空,删除节点,右孩⼦补位,返回右孩⼦为根节点
第四种情况:删除节点的右孩⼦为空,左孩⼦不为空,删除节点,左孩⼦补位,返回左孩⼦为根节点
第五种情况:左右孩⼦节点都不为空,则将删除节点的左⼦树头结点(左孩⼦)放到删除节点的右⼦树的最左⾯节点的左孩⼦上,返回删除节点右孩⼦为新的根节点
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
def traversal(node):
if not node:
return None
if node.val == key:
if not node.left and not node.right:
return None
if not node.left and node.right:
return node.right
if node.left and not node.right:
return node.left
p_node = node.right
while p_node.left:
p_node = p_node.left
p_node.left = node.left
return node.right
if node.val > key:
node.left = traversal(node.left)
if node.val < key:
node.right = traversal(node.right)
# return node
return traversal(root)
0452. 用最少数量的箭引爆气球【中等】
贪心算法,不需要先选择重叠数量最多的
class Solution:
def findMinArrowShots(self, points: List[List[int]]) -> int:
sorted_points = sorted(points, key=lambda x: x[0])
result = 1
l = sorted_points[0][1]
for pp in range(1, len(sorted_points)):
if sorted_points[pp][0] <= l:
l = min(sorted_points[pp][1], l)
else:
result += 1
l = sorted_points[pp][1]
return result
0454. 4Sum II【中等】
考察哈希表
- ⾸先定义 ⼀个 map,key放a和b两数之和,value 放a和b两数之和出现的次数。
- 遍历⼤A和⼤B数组,统计两个数组元素之和,和出现的次数,放到map中。
- 定义int变量count,⽤来统计 a+b+c+d = 0 出现的次数。
- 在遍历⼤C和⼤D数组,找到如果 0-(c+d) 在map中出现过的话,就⽤count把map中key对应的value也就是出现次数统计出来。
- 最后返回统计值 count 就可以了
class Solution:
def fourSumCount(self, nums1: List[int], nums2: List[int], nums3: List[int], nums4: List[int]) -> int:
AB = {} # 1.
for aa in nums1: # 2.
for bb in nums2:
if aa + bb in AB.keys():
AB[aa+bb] += 1
else:
AB[aa+bb] = 1
count = 0 # 3.
for cc in nums3: # 4.
for dd in nums4:
if -(cc + dd) in AB.keys():
count += AB[-(cc + dd)]
return count # 5.
0474. 一和零【中等】
二维背包问题
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
dp = [[0] * (n + 1) for _ in range(m + 1)] ## 创建二维动态规划数组,初始化为 0
# dp = [[0]*(n+1)]*(m+1) ## 错误创建方式!!
# 有 m n 两个维度的 01 背包问题
for ss in strs:
for i in range(m, ss.count('0')-1, -1):
for j in range(n, ss.count('1')-1, -1):
dp[i][j] = max(dp[i][j], dp[i-ss.count('0')][j-ss.count('1')]+1)
return dp[-1][-1]
0459. Repeated Substring pattern【简单】
考察字符串 KMP,类似 0028,需要想清楚 被匹配的字符串是 两个s拼接 去掉头尾;模式串是原字符串 s
class Solution:
def repeatedSubstringPattern(self, s: str) -> bool:
def get_next(ss):
j = 0
next = [0]
for i in range(1, len(ss)):
while j > 0 and ss[i] != ss[j]:
j = next[j-1]
if ss[i] == ss[j]:
j+=1
next.append(j)
return next
s_next = get_next(s)
new_s = s+s
new_s = new_s[1:-1]
j = 0
for i in range(len(new_s)):
while j > 0 and new_s[i] != s[j]:
j = s_next[j-1]
if new_s[i] == s[j]:
j += 1
if j == len(s):
return True
return False
0491. 非递减子序列【中等】
class Solution:
def __init__(self):
self.path = []
self.result = []
# self.used = set() ## 不是这里
def backtracking(self, candidates, start_idx):
if len(self.path) > 1:
self.result.append(self.path.copy()) # 每次都加入,而不是只加入叶子
used = set() ## 而是这里
for i_idx, i in enumerate(candidates[start_idx: ]):
if (self.path and i < self.path[-1]) or i in used: ## 去重
continue
self.path.append(i)
used.add(i)
self.backtracking(candidates, i_idx+start_idx+1)
self.path.pop(-1)
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
self.backtracking(nums, 0)
return self.result
0494. 目标和 【中等】
同分割等和子集
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
# 本题要如何使表达式结果为target
# 既然为target,那么就⼀定有 left组合(加法集合) - right组合(减法集合) = target
# left + right = sum,⽽sum是固定的 -> right = sum - left
# 公式来了, left - (sum - left) = target 推导出 left = (target + sum)/2 。
# target是固定的,sum是固定的,left就可以求出来。
# 此时问题就是在集合nums中找出和为left的组合。
bag_sum = sum(nums)
if abs(target) > bag_sum: return 0
if (bag_sum + target) % 2: return 0
temp = int((bag_sum + target) // 2)
dp = [0]*(temp+1)
dp[0] = 1
for i in range(len(nums)): ## 遍历物品
for j in range(temp, nums[i]-1, -1): ## 遍历容量 倒序保证每个物品只被添加一次
dp[j] += dp[j-nums[i]] ## 难点
# print('---', dp,j)
return dp[-1]
0501. 二叉搜索树中的众数【简单】
同 No.0530 考察二叉搜索树的处理
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.count = 0
self.max_count = 0
self.result = []
self.pre = None
def traversal(self, node):
if not node:
return
self.traversal(node.left)
if self.pre is not None:
if node.val == self.pre: self.count += 1
else: self.count = 1
if self.count > self.max_count:
self.result = [node.val]
self.max_count = self.count
elif self.count == self.max_count:
self.result.append(node.val)
else:
self.count = 1
self.max_count = 1
self.result = [node.val]
self.pre = node.val
self.traversal(node.right)
def findMode(self, root: Optional[TreeNode]) -> List[int]:
self.traversal(root)
return self.result
0509. 斐波那契数【简单】
class Solution:
# 1. 确定dp数组以及下标的含义:
# 斐波那契数 和 对应的idx
# 2. 确定递推公式
# 当前数为前两个数之和
# 3. dp数组如何初始化
# dp[0] = 0, dp[1] = 1
# 4. 确定遍历顺序
# 从前向后
def __init__(self):
self.dp = [0, 1]
def fib(self, n: int) -> int:
if n <= len(self.dp)-1:
return self.dp[n]
for i in range(2, n+1):
self.dp.append(self.dp[i-1]+self.dp[i-2])
return self.dp[n]
0518. 零钱兑换 II【中等】
同目标和,先物品后容量是组合数,先容量后物品是排列数
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0]*(amount+1)
dp[0] = 1
for i in range(len(coins)): ## 遍历物品
for j in range(coins[i], amount+1): ## 遍历容量 倒序保证每个物品只被添加一次
dp[j] += dp[j-coins[i]] ## 难点
return dp[-1]
0530. 二叉搜索树的最小绝对差【简单】
二叉搜索树是有序的【采用中序遍历,相当于一个有序数组】
遇到在⼆叉搜索树上求什么最值啊,差值之类的,就把它想成在⼀个有序数组上求最值,求差值,这样就简单多了
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.result = float('inf') ## 注意写在 init 中且赋值 inf
self.pre = None
def traversal(self, node):
if not node: return
self.traversal(node.left)
self.result = min(node.val-self.pre, self.result) if self.pre is not None else self.result ##
self.pre = node.val
self.traversal(node.right)
def getMinimumDifference(self, root: Optional[TreeNode]) -> int:
self.traversal(root)
return self.result
0541. Reverse String II【简单】
字符串反转操作,同 0344.
class Solution:
def reverseStr(self, s: str, k: int) -> str:
def reverse(s, i, j):
while i < j:
temp = s[i]
s[i] = s[j]
s[j] = temp
i += 1
j -= 1
return s
i = 0
s = list(s)
# 和 0344 的区别在于,对于反转区间的确定有不同选择
while i < len(s):
if len(s)-i >= 2*k:
s = reverse(s,i,i + k -1)
i=i+2*k
elif len(s)-i >= k:
s = reverse(s,i,i + k -1)
return ''.join(s)
else:
s = reverse(s,i,len(s) - 1)
return ''.join(s)
return ''.join(s)
0559. N 叉树的最大深度
同 No. 104, 可以用递归法(后序),只是需要处理所有子节点
for cc in range(len(node.children)):
cc_height = get_height(node.children[cc])
result = max(cc_height, result)
0572. 另一棵子树
同 No. 101, 但是需要遍历 root 的每个子树与 subRoot 进行比较
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
def compare(l, r):
if not l and r:
return False
elif not r and l:
return False
elif not l and not r:
return True
elif not l.val == r.val:
return False
else:
ll = compare(l.left, r.left)
rr = compare(l.right, r.right)
return ll and rr ## 相当于中,所以说是后序
# 以上类似 No.101
# 以下类似 No.102
my_que = deque()
if root: my_que.append(root)
while my_que:
current = my_que[0]
my_que.popleft()
if current.left: my_que.append(current.left)
if current.right: my_que.append(current.right)
if compare(current, subRoot):
return True
return False
0513. 找树左下角的值【中等】
同 No. 0102, 但是每层只需加入最左边的值 result.append(temp[0])
0515. 在每个树行中找最大值【中等】
同 No. 0102, 但是每层只需加入最大值 result.append(max(temp))
0538. 把二叉搜索树转化为累加树【中等】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def traversal(node, val):
if not node:
return val
if not node.left and not node.right:
node.val += val
return node.val
r_val = traversal(node.right, val)
node.val += r_val
l_val = traversal(node.left, node.val)
return l_val
traversal(root, 0)
return root
0637. 二叉树的层平均值【简单】
同 No. 0102, 但是每层只需加入平均值 result.append(mean(temp))
0617. 合并二叉树【简单】
两棵树同时遍历,把结果统一到左树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:
def traversal(tree_1, tree_2):
if not tree_1: return tree_2
if not tree_2: return tree_1
tree_1.val += tree_2.val
tree_1.left = traversal(tree_1.left, tree_2.left)
tree_1.right = traversal(tree_1.right, tree_2.right)
return tree_1
return traversal(root1, root2)
0654. 最大二叉树【中等】
同 No.0106, 只是处理对象是 nums
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def constructMaximumBinaryTree(self, nums: List[int]) -> Optional[TreeNode]:
def traversal(current_nums):
if not current_nums:
return None
val = max(current_nums)
new_node = TreeNode(val)
if len(current_nums)==1:
return new_node
val_idx = current_nums.index(val)
ll = current_nums[:val_idx]
rr = current_nums[val_idx+1:]
new_node.left = traversal(ll)
new_node.right =traversal(rr)
return new_node
return traversal(nums)
0674. 最长连续递增子序列【简单】
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
# :连续是和 300 的区别
# dp[i]: 【 以 num[i] 为结尾的 】最长递增子序列长度
# dp[i]: 初始化为1(至少包含 nums[i])
### num[i] > num[j]: max(dp[i],dp[i-1]+1)
### num[i] <= num[j]
dp = [1 for _ in range(len(nums))]
for i in range(1, len(nums)):
if nums[i] > nums[i-1]: ## 连续!! 所以没有 j
dp[i] = max(dp[i],dp[i-1]+1)
return max(dp)
0700. 二叉树中的搜索【简单】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
def traversal(current_node):
if not current_node:
return None
if current_node.val == val:
return current_node
result = traversal(current_node.left)
if result:
return result
result = traversal(current_node.right)
if result:
return result
return None
return traversal(root)
0701. 二叉搜索树中的插入操作【中等】
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
def traversal(node):
if not node:
return TreeNode(val)
if val <node.val:
node.left = traversal(node.left)
if val > node.val:
node.right = traversal(node.right)
return node
return traversal(root)
0707. Design Linked List【中等】
链表基本操作,同 0203;添加 max_index 属性方便操作
class ListNode:
def __init__(self, _val, _next=None):
self.val = _val
self.next = _next
class MyLinkedList:
def __init__(self):
self.max_index = -1
self.dumyhead = ListNode(-1)
def get(self, index: int) -> int:
if index > self.max_index:
return -1
currentNode = self.dumyhead
while index:
index -= 1
currentNode = currentNode.next
# 已移动到目标位置,操作获取
return currentNode.next.val
def addAtHead(self, val: int) -> None:
self.addAtIndex(0,val)
def addAtTail(self, val: int) -> None:
self.addAtIndex(self.max_index+1, val)
def addAtIndex(self, index: int, val: int) -> None:
if index > self.max_index + 1:
return
currentNode = self.dumyhead
while index:
index -= 1
currentNode = currentNode.next
# 已移动到目标位置,操作添加
new_node = ListNode(val, currentNode.next)
currentNode.next = new_node
self.max_index += 1
def deleteAtIndex(self, index: int) -> None:
if index > self.max_index:
return
currentNode = self.dumyhead
while index:
index -= 1
currentNode = currentNode.next
# 已移动到目标位置,操作删除
currentNode.next = currentNode.next.next
self.max_index -= 1
# Your MyLinkedList object will be instantiated and called as such:
# obj = MyLinkedList()
# param_1 = obj.get(index)
# obj.addAtHead(val)
# obj.addAtTail(val)
# obj.addAtIndex(index,val)
# obj.deleteAtIndex(index)
0704. 二分查找【简单】
我们定义 target 是在⼀个在左闭右闭的区间⾥,也就是[left, right]
-
if (nums[middle] > target) right要赋值为middle - 1,因为当前这个nums[middle]⼀定不是target,那么接下来要查找的左区间结束下标位置就是middle - 1 -
例如在数组:1,2,3,4,7,9,10中查找元素2: 接下来要查找的左区间结束下标位置 应该是2而不是3
# 时间复杂度 O(logn), 空间复杂度 O(1)
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # 定义target在左闭右闭的区间里,[left, right]
while left <= right:
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle - 1 # target在左区间,所以[left, middle - 1]
elif nums[middle] < target:
left = middle + 1 # target在右区间,所以[middle + 1, right]
else:
return middle # 数组中找到目标值,直接返回下标
return -1 # 未找到目标值
0714. 买卖股票的最佳时机含手续费
同 No.0122 II 但是有手续费 fee
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
if len(prices) == 0: return 0
dp = [[-prices[0],0] for i in range(len(prices))]
for i in range(1,len(prices)):
dp[i][0] = max(dp[i-1][0], -prices[i]+ dp[i-1][1])
dp[i][1] = max(dp[i-1][1], prices[i]+dp[i-1][0]-fee) # *** 区别点在于此
return dp[-1][1]
0718. 最长连续子数组【中等】
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
# ⽤⼆维数组可以记录两个字符串的所有⽐较情况
# dp[i][j]: 以下标 i-1 为结尾的A,和以下标 j-1 为结尾的B,
# 最⻓重复⼦数组⻓度为dp[i][j]
result = 0
dp = [[0 for _ in range(len(nums2)+1)] for _ in range(len(nums1)+1)]
for i in range(1, len(nums1)+1):
for j in range(1, len(nums2)+1):
if nums1[i-1] == nums2[j-1]: ## 递推
dp[i][j] = dp[i-1][j-1]+ 1
if dp[i][j] > result: result = dp[i][j]
return result
0738. 单调递增的数字【中等】
class Solution:
def monotoneIncreasingDigits(self, n: int) -> int:
string_n = list(str(n)) ##
flag = len(string_n)
for i in range(len(string_n)-1, 0, -1):
if string_n[i-1] > string_n[i]:
flag = i
string_n[i-1] = chr(ord(string_n[i-1]) - 1) ##
for i in range(flag, len(string_n)):
string_n[i] = '9'
return int(''.join(string_n))
0746. 使用最小花费爬楼梯【简单】
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
self.min_cost = [0, 0, min(cost[0], cost[1])]
for i in range(3, len(cost)+1):
self.min_cost.append(min(cost[i-1]+self.min_cost[i-1], cost[i-2]+self.min_cost[i-2]))
return self.min_cost[-1]
0763. 划分字母区间【中等】
class Solution:
def partitionLabels(self, s: str) -> List[int]:
# 统计区间
table_dict = {}
for s_idx, ss in enumerate(s):
if ss in table_dict.keys():
table_dict[ss][1] = s_idx
else:
table_dict[ss] = [s_idx,s_idx]
# 区间划分
result = [0]
r_pos = 0
for s_idx, ss in enumerate(s):
result[-1] += 1
r_pos = max(r_pos, table_dict[ss][1])
if s_idx == r_pos:
result.append(0)
r_pos = table_dict[ss][1]
return result[:-1]
0844. Backspace String Compare【简单】
考察双指针法,同 0027,附加以倒序处理backspace的思路;用快指针找到 real (最终没被删除的) index 位置值用来进行后续判断
# 时间复杂度 O(n), 空间复杂度 O(1)
class Solution(object):
def backspaceCompare(self, s, t):
# 找到当前位置上的有效字符
def get_real_index(current_string, index):
# 从当前索引开始向前遍历,直到找到前一个有效字符的索引位置
count = 0
while index >=0:
if current_string[index] == '#':
count += 1
else:
if count > 0:
count -= 1
else:
return index
index -= 1
return index
# 将两个指针 i 和 j 分别初始化为字符串 s 和 t 的最后一个字符的索引
ss = len(s) - 1
tt = len(t) - 1
# 从后向前遍历两个字符串
while ss>=0 or tt>=0:
ss = get_real_index(s, ss)
tt = get_real_index(t, tt)
if ss < 0 and tt < 0: # 如果两个指针都到达了字符串的开头,且在迭代的过程中没有出现字符不相等的情况,那么这两个字符串是相等的,返回 True
return True
elif ss>=0 and tt>=0 and s[ss] == t[tt]: # 比较两个字符串在当前位置上的字符是否相等。如果相等,则继续迭代到下一个位置,否则返回 False
ss -= 1
tt -= 1
else: # 如果其中一个字符串达到了开头(索引为 -1),而另一个字符串还未到达开头,那么这两个字符串的长度不同,因此它们不可能相等,返回 False
return False
return True
0860. 柠檬水找零【简单】
直接模拟 + 20 面额时贪心
class Solution:
def lemonadeChange(self, bills: List[int]) -> bool:
cash = {5:0, 10:0, 20:0}
for i in bills:
cash[i] += 1
if i == 5:
continue
if i == 10:
if cash[5] >= 1:
cash[5] -= 1
else:
return False
if i == 20:
if cash[10] >= 1:
cash[10] -= 1
if cash[5] >= 1:
cash[5] -= 1
else:
return False
else:
if cash[5] >= 3:
cash[5] -= 3
else:
return False
return True
0904. Fruit Into Backets【中等】
考察滑动窗口法,同 0209
class Solution(object):
def totalFruit(self, fruits):
i = 0
result = 0
types = Counter() # 用来跟踪值出现的次数
for j, jj in enumerate(fruits): # 既需要 value 又需要 index
types[jj] += 1
while len(types) > 2: # 窗口起始移动条件符合
types[fruits[i]] -= 1
if types[fruits[i]] == 0:
types.pop(fruits[i])
i += 1
result = max(j-i+1, result) # 对符合条件的区间进行操作
return result
0968. 监督二叉树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.result = 0
def traversal(self, current_node):
if not current_node:
return 2 ## 有覆盖
left = self.traversal(current_node.left)
right = self.traversal(current_node.right)
if left == 2 and right == 2: ## 都有覆盖
return 0
if left == 0 or right == 0: ## 存在无覆盖
self.result += 1
return 1
if left == 1 or right == 1: ## 存在摄像头
return 2
def minCameraCover(self, root: Optional[TreeNode]) -> int:
if self.traversal(root) == 0:
self.result += 1 ## 应对根节点无覆盖的特殊情况
return self.result
0977. Squares of a Sorted Array【简单】
考察双指针法,同 0027,因为元素有正负之分,所以从两侧用两个指针同时处理
class Solution(object):
def sortedSquares(self, nums):
index_l = 0
index_r = len(nums) - 1
new_nums = []
while index_l < index_r:
print(nums[index_l], nums[index_r])
if nums[index_r] + nums[index_l] > 0:
new_nums = [nums[index_r]**2] + new_nums
index_r -= 1
else:
new_nums = [nums[index_l]**2] + new_nums
index_l += 1
return [nums[index_l]**2] + new_nums
1005. K 次取反后最大化的数组和【简单】
class Solution:
def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
while k > 0:
nums.sort()
nums[0] = -nums[0]
k -= 1
return sum(nums)
1035 .
同 NO.1143
1047. 删除字符串中所有相邻重复项
同 No.0020, 考察栈操作
class Solution:
def removeDuplicates(self, s: str) -> str:
result = []
for ss in s:
if result and ss == result[-1]:
result.pop()
else:
result.append(ss)
return ''.join(result)
1049. 最后一块石头的重量【中等】
同 分割等和字迹
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
bag_sum = sum(stones)
target = int(bag_sum // 2) ##
dp = [0]*(target+1)
for i in range(len(stones)): ## 遍历物品
for j in range(target, stones[i]-1, -1): ## 遍历容量 倒序保证每个物品只被添加一次
dp[j] = max(dp[j], dp[j-stones[i]] + stones[i])
return bag_sum-dp[-1]-dp[-1] ##
1143. 最长公共子序列
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
# 注意:元素之间可以不连续
# ⽤⼆维数组可以记录两个字符串的所有⽐较情况
# dp[i][j]: 以下标 i-1 为结尾的A,和以下标 j-1 为结尾的B,
# 最⻓重复⼦数组⻓度为dp[i][j]
result = 0
dp = [[0 for _ in range(len(text2)+1)] for _ in range(len(text1)+1)]
for i in range(1, len(text1)+1):
for j in range(1, len(text2)+1):
if text1[i-1] == text2[j-1]: ## 递推
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
if dp[i][j] > result: result = dp[i][j]
return result