目录
一、基础知识
1. 图的种类
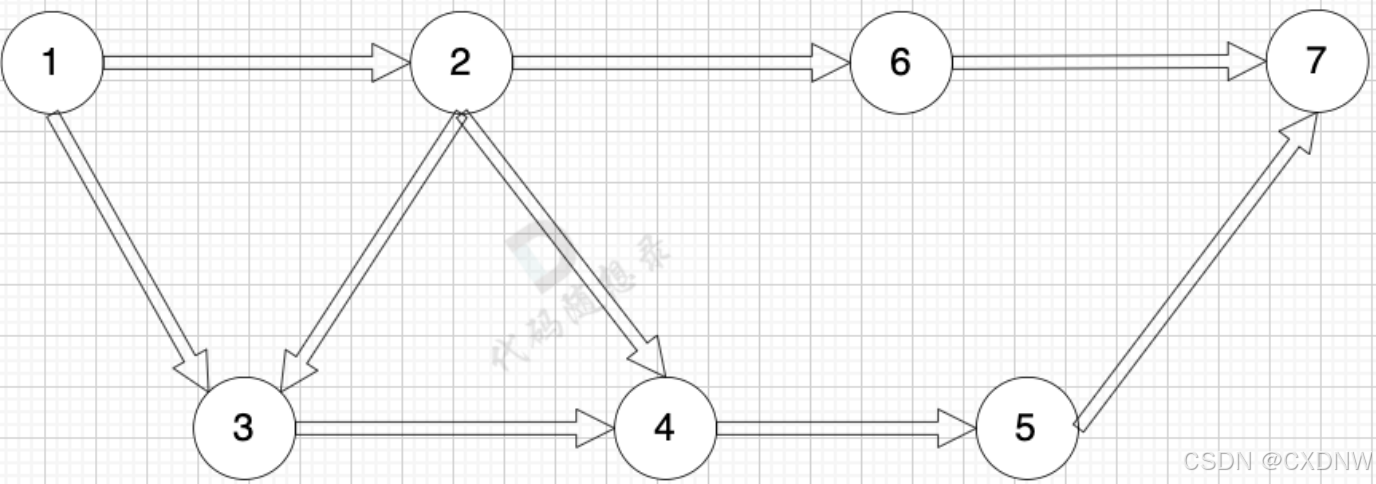
(1)有向图
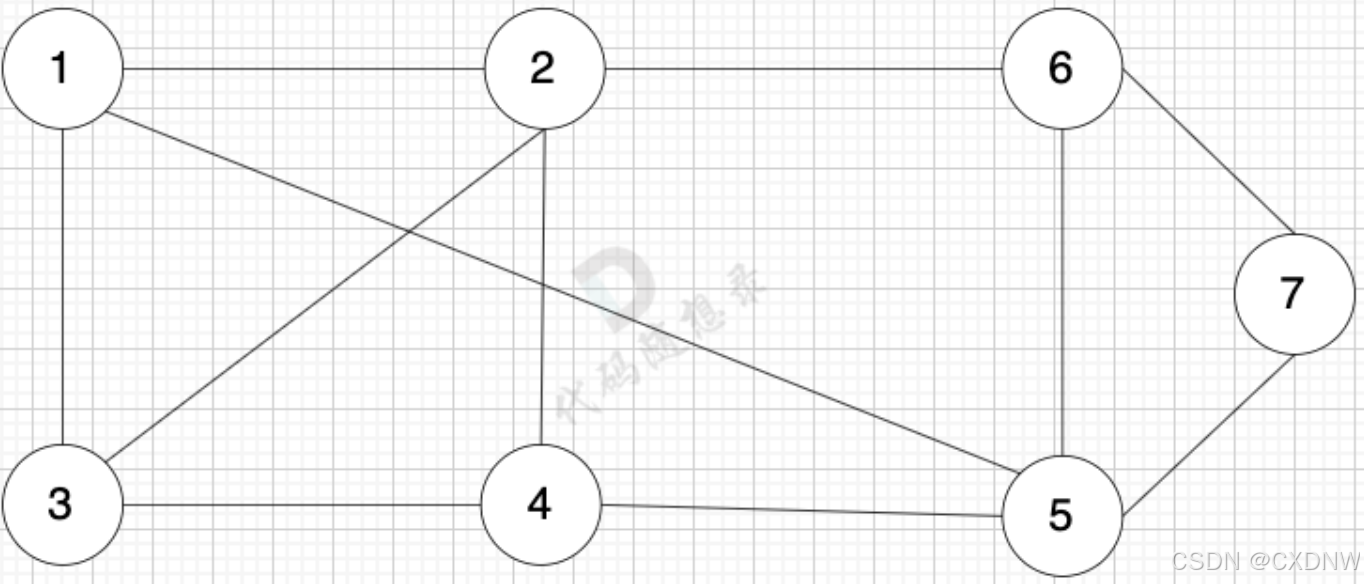
(2)无向图
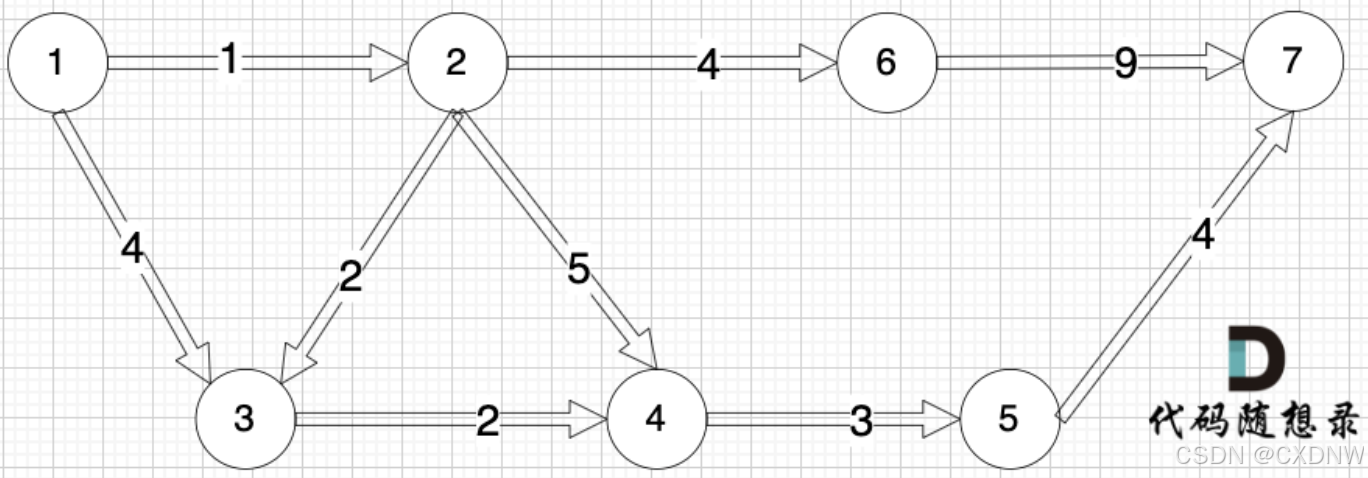
(3)加权有向图
2. 图的构造
(1)邻接矩阵
邻接矩阵 使用 二维数组来表示图结构。 邻接矩阵是从节点的角度来表示图,有多少节点就申请多大的二维数组。
例如:
grid[2][5] = 6,表示 节点 2 连接 节点 5 为 有向图,节点 2 指向 节点 5,边的 权值为 6。
如果想 表示 无向图,即:grid[2][5] = 6,grid[5][2] = 6,表示 节点 2 与 节点 5 相互连通,权值为6。
邻接矩阵的优点:
- 表达方式 简单,易于 理解。
- 检查 任意两个顶点间 是否 存在边的 操作 非常快。
- 适合 稠密图,在边数 接近 顶点数 平方的图中,邻接矩阵 是一种 空间效率 较高的 表示方法。
缺点:
- 遇到 稀疏图,会 导致申请 过大的 二维数组造成空间浪费 且遍历 边 的时候 需要 遍历整个 n * n 矩阵,造成 时间 浪费。
(2)邻接表
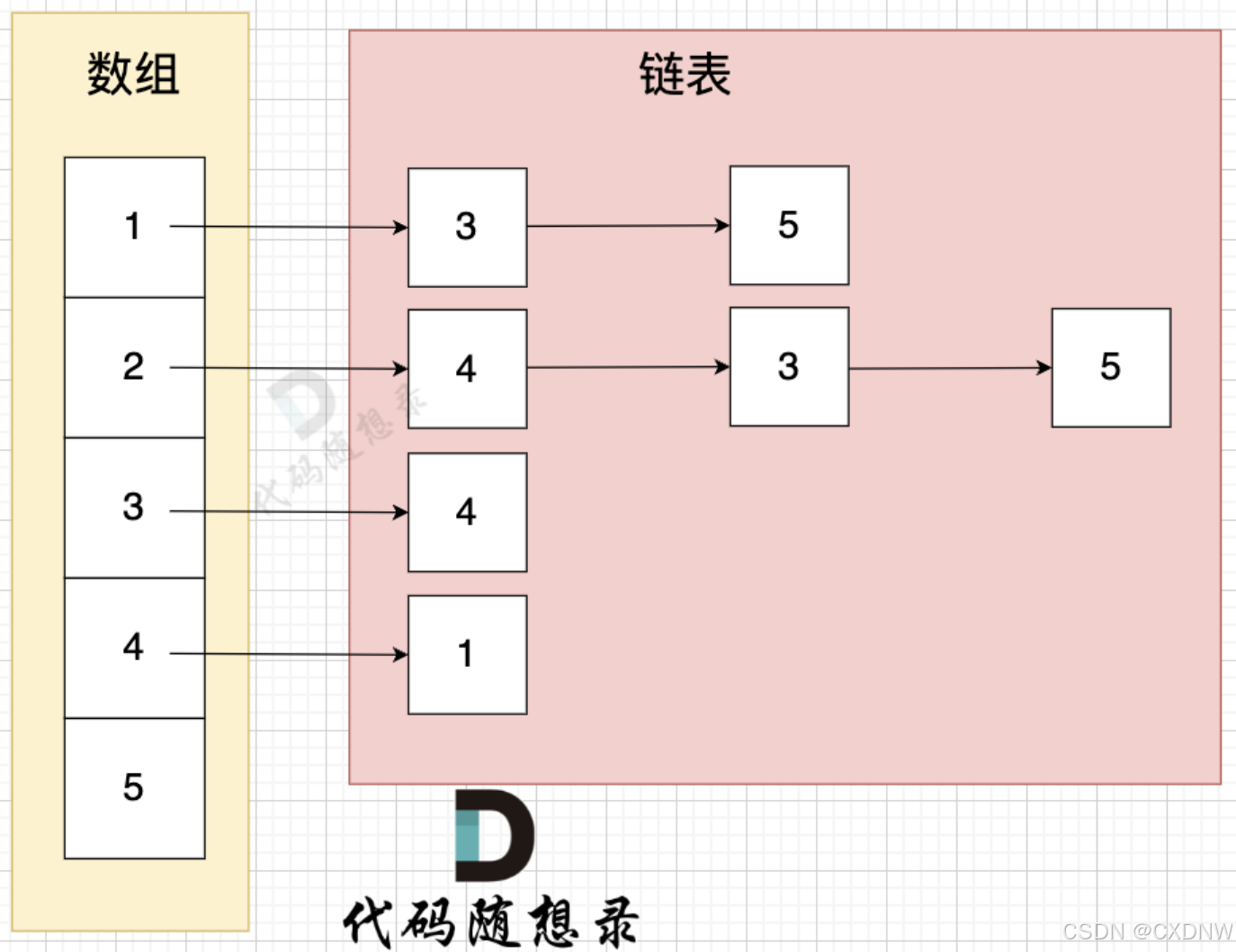
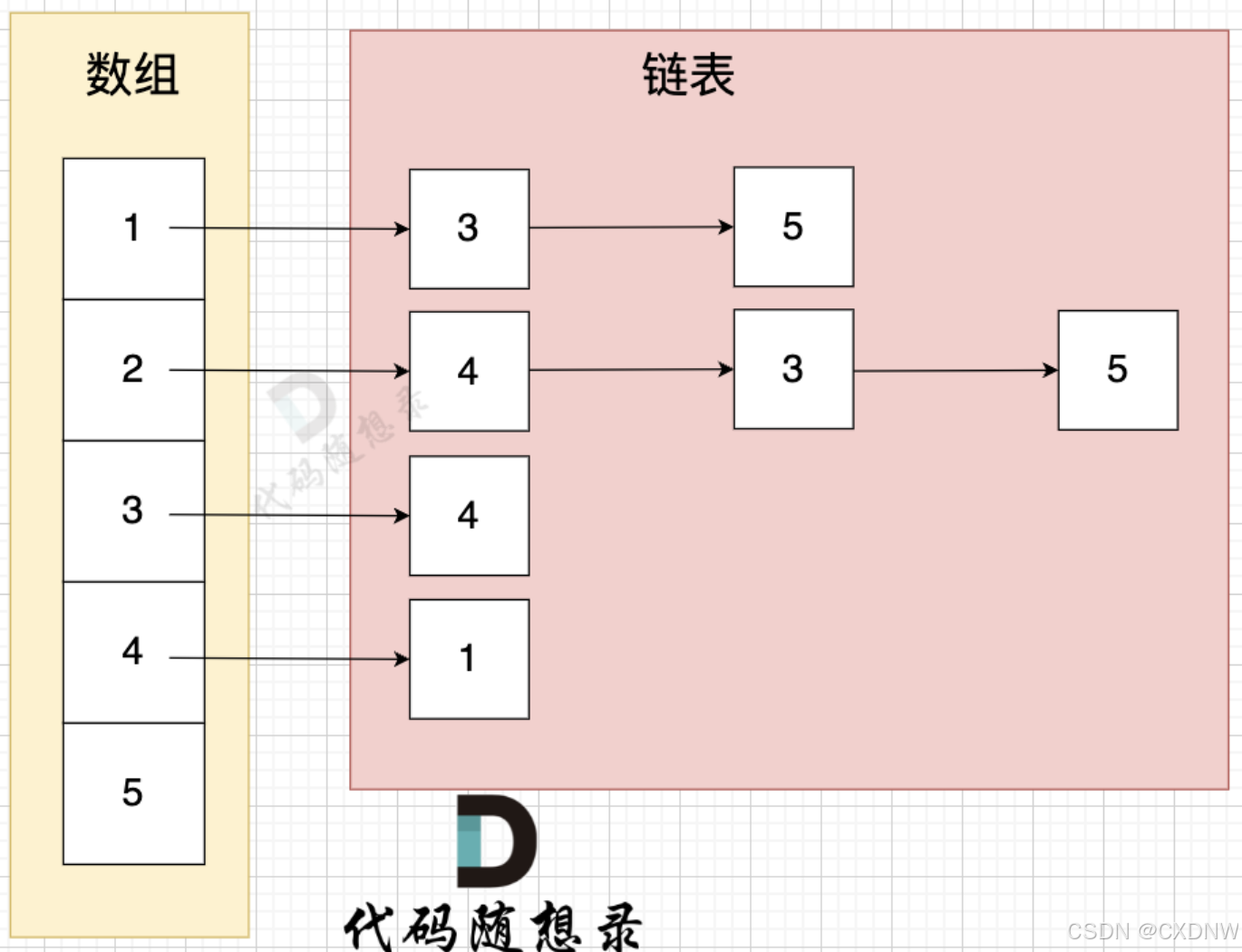
邻接表 使用 数组 + 链表的方式来 表示。 邻接表 是从 边的数量 来表示图,有多少边 才会申请 对应大小的 链表。
上图表示为
- 节点 1 指向 节点 3 和 节点 5
- 节点 2 指向 节点 4、节点 3、节点 5
- 节点 3 指向 节点 4
- 节点 4 指向 节点 1
邻接表的优点:
- 对于 稀疏图的存储,只需要 存储边,空间 利用率高。
- 遍历 节点 连接情况 相对容易。
缺点:
- 检查任 意两个节点间 是否存在 边,效率 相对低,需要 O(V) 时间,V 表示某 节点 连接其他 节点的 数量。
- 实现 相对复杂,不易 理解。
3. 图的遍历方式
(1)深度优先搜索(dfs)
// 代码框架
void dfs(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本节点所连接的其他节点) {
处理节点;
dfs(图,选择的节点); // 递归
回溯,撤销处理结果
}
}(2)广度优先搜索(bfs)
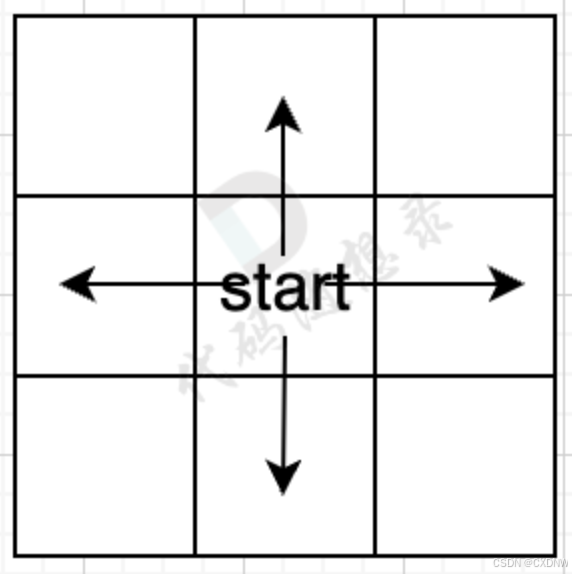
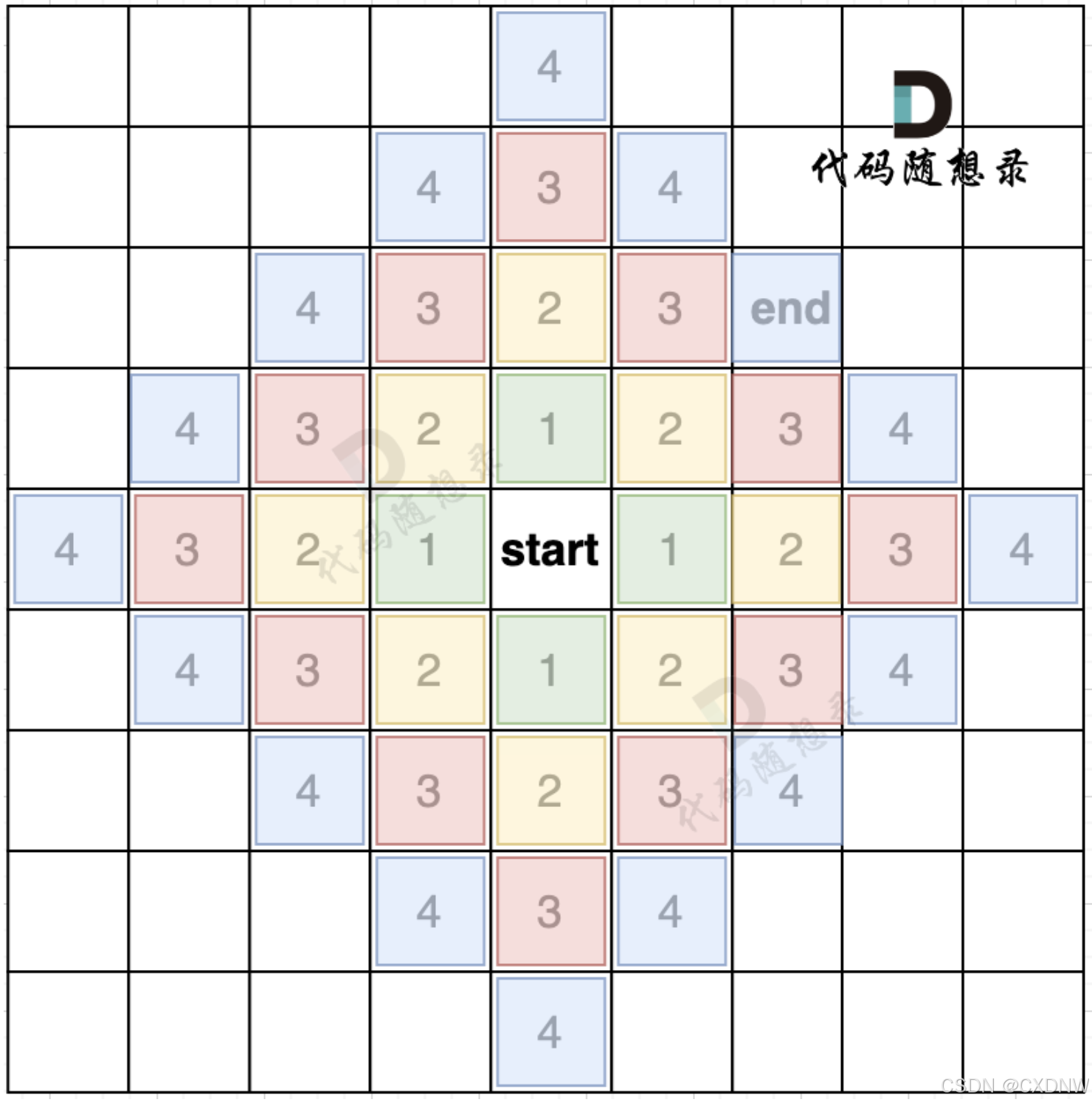
用一个方格地图,假如每次搜索的方向为 上下左右(不包含斜上方),那么给出一个start起始位置,那么BFS就是从四个方向走出第一步。
// 代码框架
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图,也就是一个二维数组
// visited标记访问过的节点,不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que; // 定义队列
que.push({x, y}); // 起始节点加入队列
visited[x][y] = true; // 只要加入队列,立刻标记为访问过的节点
while(!que.empty()) { // 开始遍历队列里的元素
pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
int curx = cur.first;
int cury = cur.second; // 当前节点坐标
for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 坐标越界了,直接跳过
if (!visited[nextx][nexty]) { // 如果节点没被访问过
que.push({nextx, nexty}); // 队列添加该节点为下一轮要遍历的节点
visited[nextx][nexty] = true; // 只要加入队列立刻标记,避免重复访问
}
}
}
}二、相关题目
1. 所有可达路径
98. 所有可达路径
给定一个有 n 个节点的有向无环图,节点编号从 1 到 n。请编写一个函数,找出并返回所有从节点 1 到节点 n 的路径。每条路径应以节点编号的列表形式表示。
输入描述
第一行包含两个整数 N,M,表示图中拥有 N 个节点,M 条边
后续 M 行,每行包含两个整数 s 和 t,表示图中的 s 节点与 t 节点中有一条路径
输出描述
输出所有的可达路径,路径中所有节点之间空格隔开,每条路径独占一行,存在多条路径,路径输出的顺序可任意。如果不存在任何一条路径,则输出 -1。
注意输出的序列中,最后一个节点后面没有空格! 例如正确的答案是 `1 3 5`,而不是 `1 3 5 `, 5后面没有空格!输入示例
5 5
1 3
3 5
1 2
2 4
4 5输出示例
1 3 5
1 2 4 5
(1)邻接矩阵表示
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void dfs (const vector<vector<int>>& graph, int x, int n) {
if (x == n) {
result.push_back(path);
return ;
}
for (int i = 1; i <= n; i++) {
// 找到 n 指向的节点
if (graph[x][i] == 1) {
path.push_back(i);
dfs(graph, i, n);
path.pop_back();
}
}
}
int main() {
// 获取数据
int n, m, s, t;
cin >> n >> m;
vector<vector<int>> graph(n + 1, vector<int>(n + 1, 0));
while (m--) {
cin >> s >> t;
// s 指向 t
graph[s][t] = 1;
}
// 都是从 1 开始
path.push_back(1);
dfs(graph, 1, n); // 当前遍历节点 1
// 打印
if (result.size() == 0) cout << -1 << endl;
for (const vector<int> &pa : result) {
for (int i = 0; i < pa.size() - 1; i++) {
cout << pa[i] << " ";
}
cout << pa[pa.size() - 1] << endl;
}
return 0;
}(2)邻接表法
#include <iostream>
#include <vector>
#include <list>
using namespace std;
vector<vector<int>> result;
vector<int> path;
void dfs (const vector<list<int>>& graph, int x, int n) {
if (x == n) {
result.push_back(path);
return ;
}
for (int i : graph[x]) {
// 找到 x 指向的链表
path.push_back(i);
dfs(graph, i, n);
path.pop_back();
}
}
int main() {
// 邻接表解法
// 获取数据
int n, m, s, t;
cin >> n >> m;
vector<list<int>> graph(n + 1);
while (m--) {
cin >> s >> t;
// s 指向 t
graph[s].push_back(t);
}
// 都是从 1 开始
path.push_back(1);
dfs(graph, 1, n); // 当前遍历节点 1
// 打印
if (result.size() == 0) cout << -1 << endl;
for (const vector<int> &pa : result) {
for (int i = 0; i < pa.size() - 1; i++) {
cout << pa[i] << " ";
}
cout << pa[pa.size() - 1] << endl;
}
return 0;
}2. 岛屿数量
99. 岛屿数量
给定一个由 1(陆地)和 0(水)组成的矩阵,你需要计算岛屿的数量。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。
后续 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示岛屿的数量。如果不存在岛屿,则输出 0。输入示例
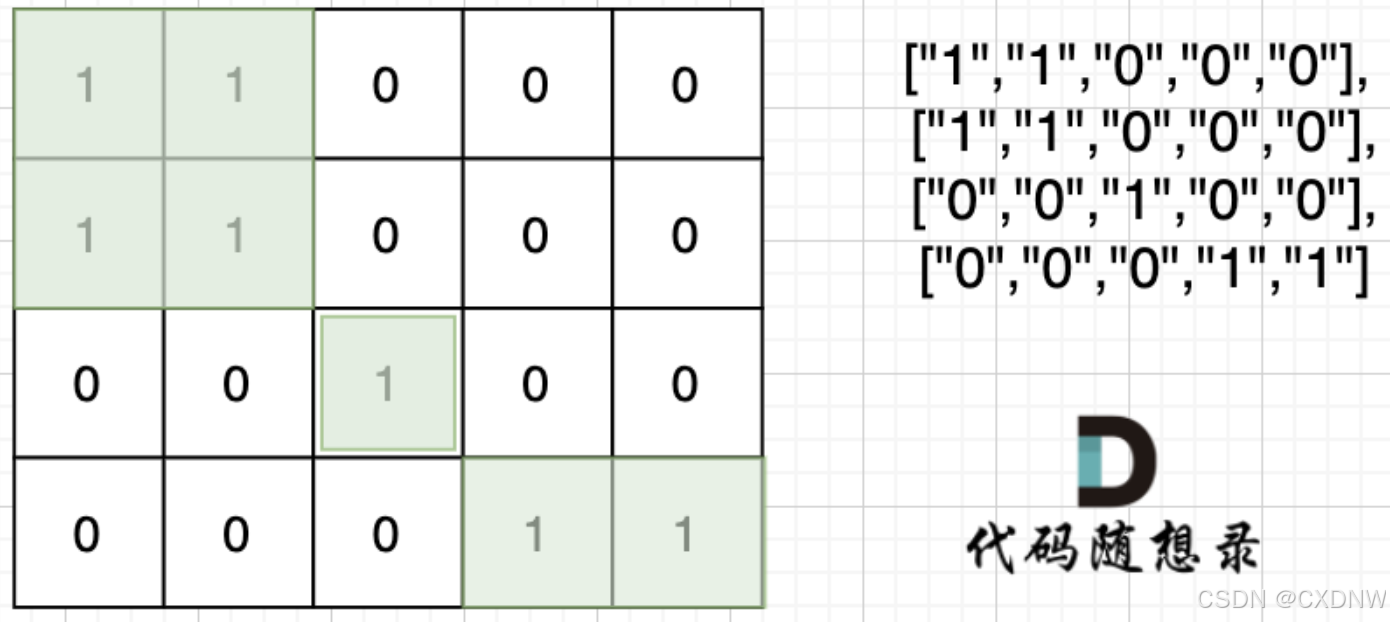
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1输出示例
3思路:
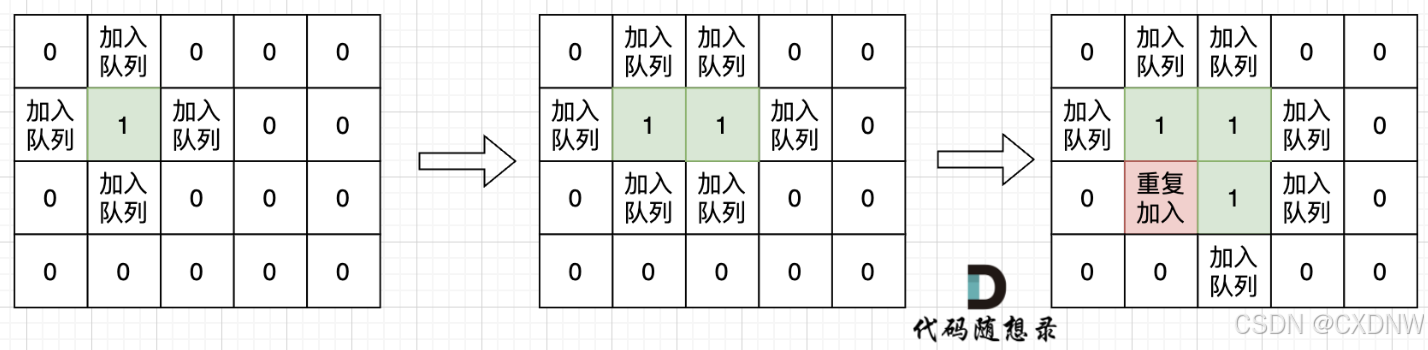
用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。
在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。
(1)深度优先搜索
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {0, -1, 0, 1, -1, 0, 1, 0}; // 记录上下左右坐标
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超出范围直接跳过
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (grid[nextx][nexty] == 1 && !visited[nextx][nexty]) {
visited[nextx][nexty] = true;
dfs(grid, visited, nextx, nexty);
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 记录是否为同一块陆地
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 如果遍历到的陆地没有被占,那么陆地的数量 +1
// 并且将陆地上的所有板块全部标记
if (grid[i][j] == 1 && !visited[i][j]) {
result++;
visited[i][j] = true;
dfs(grid, visited, i, j);
}
}
}
cout << result << endl;
return 0;
}(2)广度优先搜索
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int dir[4][2] = {0, -1, 0, 1, -1, 0, 1, 0}; // 记录上下左右坐标
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
// 广度优选算法
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 加入队列后立即保存当前位置
while (!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = dir[i][0] + curx;
int nexty = dir[i][1] + cury;
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (grid[nextx][nexty] == 1 && !visited[nextx][nexty]) {
dfs(grid, visited, nextx, nexty);
}
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 记录是否为同一块陆地
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
// 如果遍历到的陆地没有被占,那么陆地的数量 +1
// 并且将陆地上的所有板块全部标记
if (grid[i][j] == 1 && !visited[i][j]) {
result++;
visited[i][j] = true;
dfs(grid, visited, i, j);
}
}
}
cout << result << endl;
return 0;
}3. 岛屿的最大面积
100. 岛屿的最大面积
给定一个由 1(陆地)和 0(水)组成的矩阵,计算岛屿的最大面积。岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿由水平方向或垂直方向上相邻的陆地连接而成,并且四周都是水域。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。后续 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的最大面积。如果不存在岛屿,则输出 0。输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1输出示例
4(1)深度优先搜索
#include <iostream>
#include <vector>
using namespace std;
int count;
int dir[4][2] = {1, 0, -1, 0, 0, 1, 0, -1};
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
visited[nextx][nexty] = true;
count++;
dfs(grid, visited, nextx, nexty);
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
// dfs处理下一个节点,所以count初值为0
count = 1;
visited[i][j] = true;
dfs(grid, visited, i, j);
result = max(result, count);
}
}
}
cout << result << endl;
return 0;
}
(2)广度优先搜索
class Solution {
private:
int count;
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<int> que;
que.push(x);
que.push(y);
visited[x][y] = true; // 加入队列就意味节点是陆地可到达的点
count++;
while(!que.empty()) {
int xx = que.front();que.pop();
int yy = que.front();que.pop();
for (int i = 0 ;i < 4; i++) {
int nextx = xx + dir[i][0];
int nexty = yy + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界
if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 节点没有被访问过且是陆地
visited[nextx][nexty] = true;
count++;
que.push(nextx);
que.push(nexty);
}
}
}
}
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
result = max(result, count);
}
}
}
return result;
}
};4. 孤岛的总面积
101. 孤岛的总面积
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要计算所有孤岛的总面积,岛屿面积的计算方式为组成岛屿的陆地的总数。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0。
输出描述
输出一个整数,表示所有孤岛的总面积,如果不存在孤岛,则输出 0。输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1输出示例
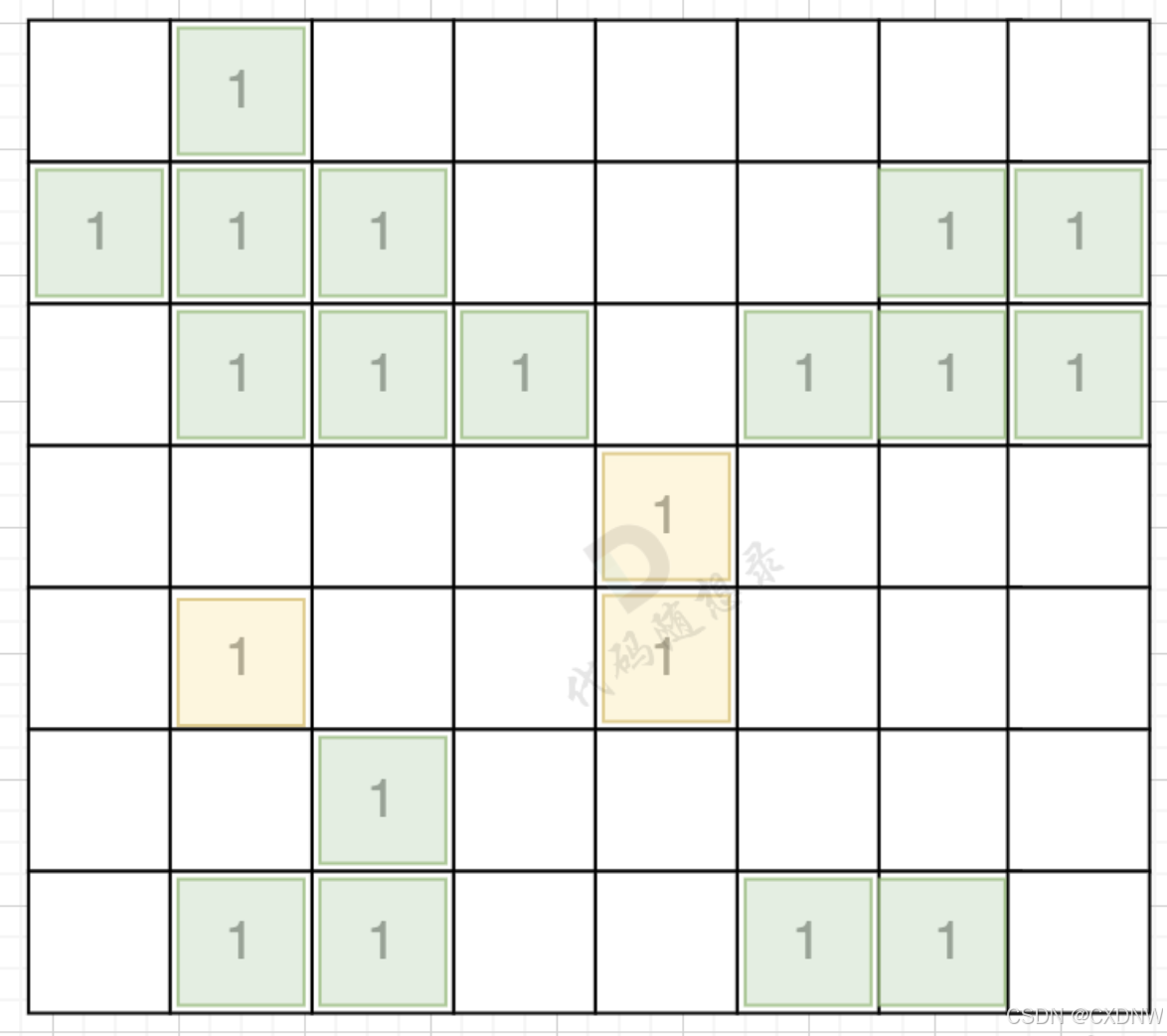
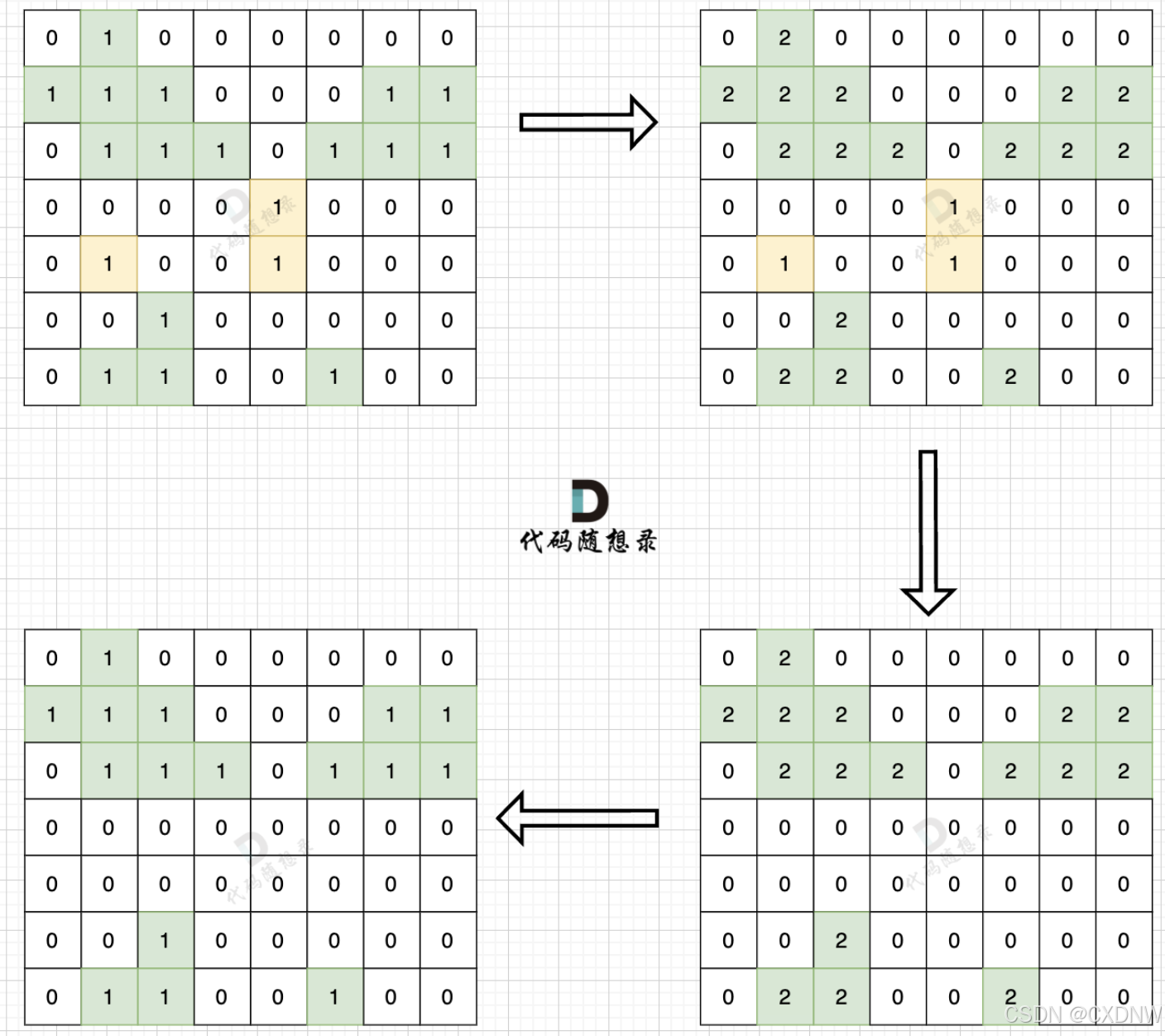
1思路:
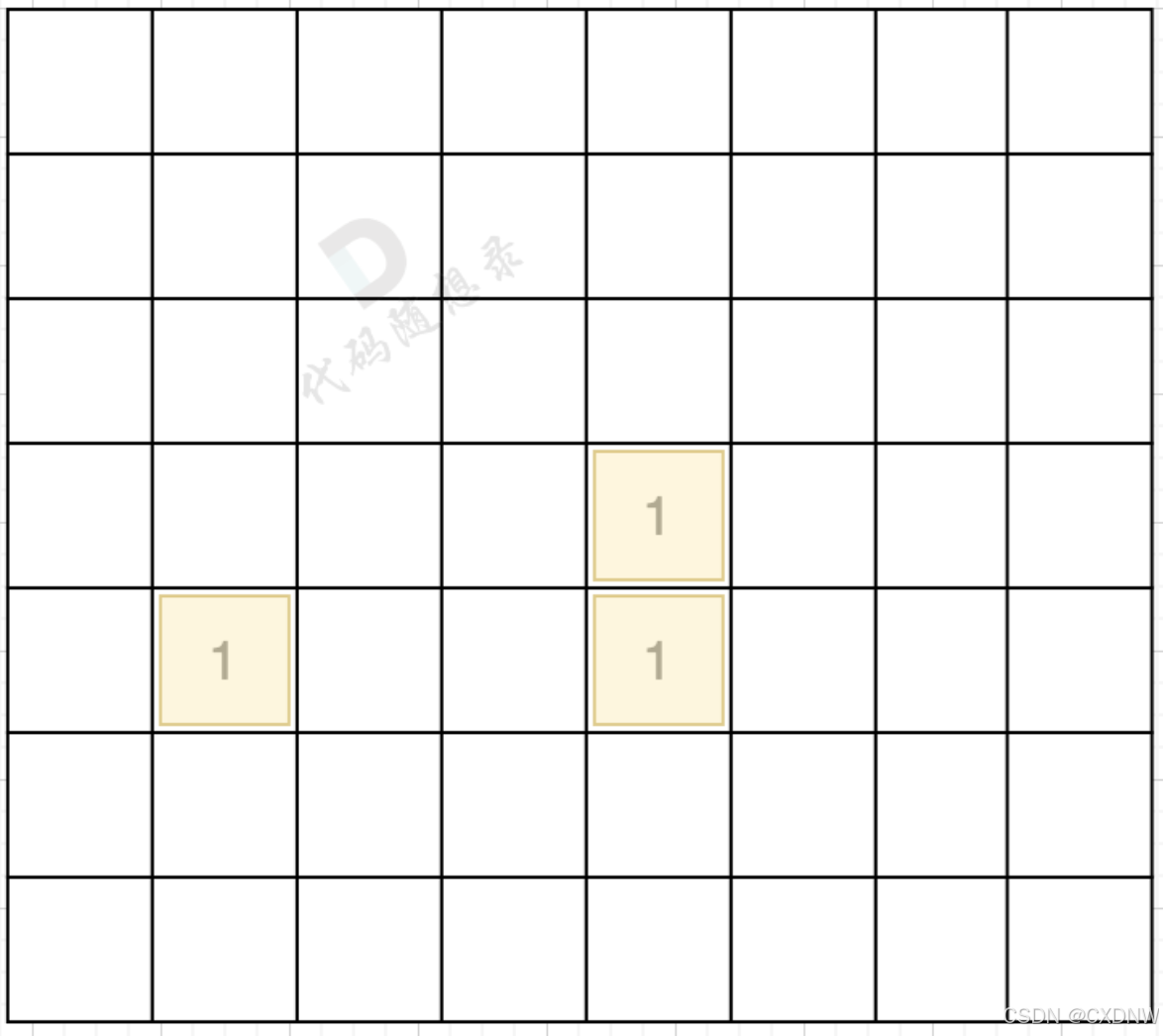
在遇到地图周边陆地的时候,将1都变为0,此时地图为这样:
然后我们再去遍历这个地图,遇到有陆地的地方,去采用深搜或者广搜,边统计所有陆地。
// 深度优先搜索
#include <iostream>
#include <vector>
using namespace std;
int count;
int dir[4][2] = {1, 0, -1, 0, 0, 1, 0, -1};
void dfs(vector<vector<int>>& grid, int x, int y) {
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (grid[nextx][nexty] == 1) {
grid[nextx][nexty] = 0;
dfs(grid, nextx, nexty);
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n , vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
int result = 0;
// 左右两边岛屿
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) dfs(grid, i, 0);
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
}
// 上下两边岛屿
for (int i = 0; i < m; i++) {
if (grid[0][i] == 1) dfs(grid, 0, i);
if (grid[n - 1][i] == 1) dfs(grid, n - 1, i);
}
// 计算孤岛总面积
for (int i = 1; i < n - 1; i++) {
for (int j = 1; j < m - 1; j++) {
if (grid[i][j] == 1) result++;
}
}
cout << result << endl;
return 0;
}5. 沉没孤岛
102. 沉没孤岛
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿指的是由水平或垂直方向上相邻的陆地单元格组成的区域,且完全被水域单元格包围。孤岛是那些位于矩阵内部、所有单元格都不接触边缘的岛屿。
现在你需要将所有孤岛“沉没”,即将孤岛中的所有陆地单元格(1)转变为水域单元格(0)。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。
之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出将孤岛“沉没”之后的岛屿矩阵。 注意:每个元素后面都有一个空格输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1输出示例
1 1 0 0 0
1 1 0 0 0
0 0 0 0 0
0 0 0 1 1思路:
定义一个 visited 二维数组,单独标记 周边的陆地,然后 遍历地图 的时候同时对 数组 board 和 数组 visited 进行判断,决定 陆地是否变成水域。
- 步骤一:深搜或者广搜将地图周边的 1 (陆地)全部改成 2 (特殊标记)
- 步骤二:将水域中间 1 (陆地)全部改成 水域(0)
- 步骤三:将之前标记的 2 改为 1 (陆地)
// 深度优先搜索
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
void dfs(vector<vector<int>>& grid, int x, int y) {
grid[x][y] = 2;
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
// 不符合条件,不继续遍历
if (grid[nextx][nexty] == 0 || grid[nextx][nexty] == 2) continue;
dfs (grid, nextx, nexty);
}
return;
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
// 步骤一:
// 从左侧边和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (grid[i][0] == 1) dfs(grid, i, 0);
if (grid[i][m - 1] == 1) dfs(grid, i, m - 1);
}
// 从上边和下边向中间遍历
for (int j = 0; j < m; j++) {
if (grid[0][j] == 1) dfs(grid, 0, j);
if (grid[n - 1][j] == 1) dfs(grid, n - 1, j);
}
// 步骤二、步骤三
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) grid[i][j] = 0;
if (grid[i][j] == 2) grid[i][j] = 1;
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cout << grid[i][j] << " ";
}
cout << endl;
}
}6. 水流问题
103. 水流问题
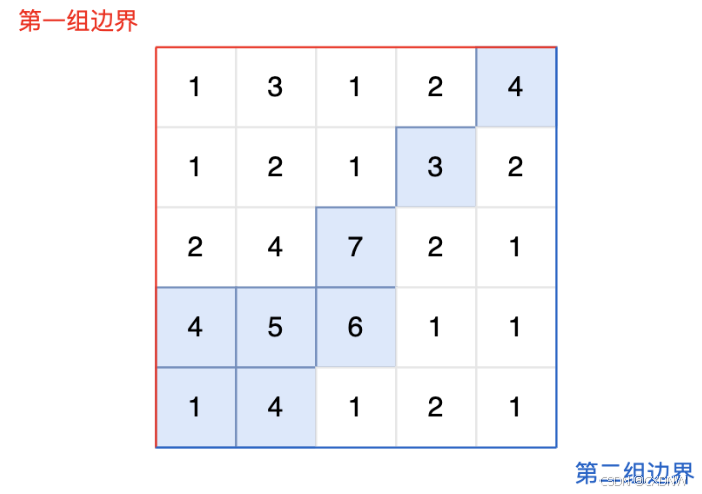
现有一个 N × M 的矩阵,每个单元格包含一个数值,这个数值代表该位置的相对高度。矩阵的左边界和上边界被认为是第一组边界,而矩阵的右边界和下边界被视为第二组边界。
矩阵模拟了一个地形,当雨水落在上面时,水会根据地形的倾斜向低处流动,但只能从较高或等高的地点流向较低或等高并且相邻(上下左右方向)的地点。我们的目标是确定那些单元格,从这些单元格出发的水可以达到第一组边界和第二组边界。
输入描述
第一行包含两个整数 N 和 M,分别表示矩阵的行数和列数。
后续 N 行,每行包含 M 个整数,表示矩阵中的每个单元格的高度。
输出描述
输出共有多行,每行输出两个整数,用一个空格隔开,表示可达第一组边界和第二组边界的单元格的坐标,输出顺序任意。输入示例
5 5
1 3 1 2 4
1 2 1 3 2
2 4 7 2 1
4 5 6 1 1
1 4 1 2 1输出示例
0 4
1 3
2 2
3 0
3 1
3 2
4 0
4 1思路:
遍历每个点,然后看这个点 能不能同时到达第一组边界和第二组边界。
#include <iostream>
#include <vector>
using namespace std;
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1};
void dfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (visited[x][y]) return;
visited[x][y] = true;
for (int i = 0; i < 4; i++) {
int nextx = dir[i][0] + x;
int nexty = dir[i][1] + y;
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (grid[x][y] > grid[nextx][nexty]) continue;
dfs(grid, visited, nextx, nexty);
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visitedleft(n, vector<bool>(m, false));
vector<vector<bool>> visitedright(n, vector<bool>(m, false));
// 上下
for (int i = 0; i < m; i++) {
dfs(grid, visitedleft, 0, i);
dfs(grid, visitedright, n - 1, i);
}
// 左右
for (int i = 0; i < n; i++) {
dfs(grid, visitedleft, i, 0);
dfs(grid, visitedright, i, m - 1);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (visitedleft[i][j] && visitedright[i][j]) {
cout << i << " " << j << endl;
}
}
}
return 0;
}7. 建造最大岛屿
104. 建造最大岛屿
给定一个由 1(陆地)和 0(水)组成的矩阵,你最多可以将矩阵中的一格水变为一块陆地,在执行了此操作之后,矩阵中最大的岛屿面积是多少。
岛屿面积的计算方式为组成岛屿的陆地的总数。岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设矩阵外均被水包围。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示最大的岛屿面积。输入示例
4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1输出示例
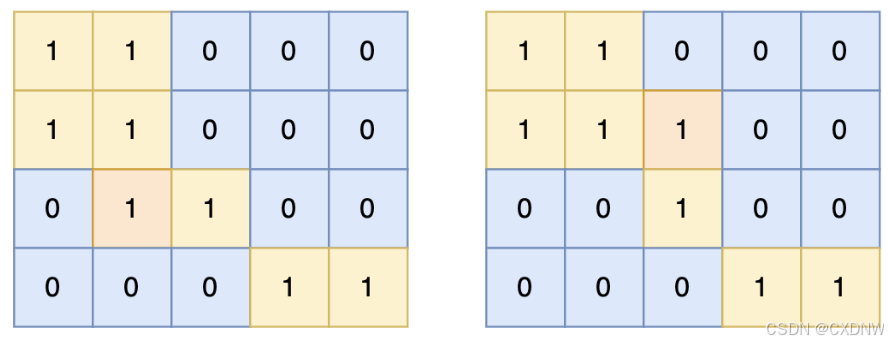
6思路:
第一步:一次遍历地图,得出 各个岛屿的面积,并做编号记录。可以使用 map 记录,key 为岛屿编号,value 为岛屿面积
第二步:再遍历地图,遍历 0 的方格(因为要将 0 变成 1),并统计该 1(由 0 变成的 1)周边岛屿面积,将其 相邻面积 相加在一起,遍历所有 0 之后,就可以得出 选一个 0 变成 1 之后的最大面积。
#include <iostream>
#include <vector>
#include <unordered_map>
#include <unordered_set>
using namespace std;
int dir[4][2] = {1, 0, -1, 0, 0, 1, 0, -1};
int count;
void dfs(vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y, int sign) {
if (visited[x][y] || grid[x][y] == 0) return;
visited[x][y] = true;
grid[x][y] = sign;
count++;
for (int i = 0; i < 4; i++) {
int nextx = dir[i][0] + x;
int nexty = dir[i][1] + y;
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
dfs(grid, visited, nextx, nexty, sign);
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false));
unordered_map<int, int> gridNum;
int signals = 2;
bool isAllGrid = true;
// 为每一个岛屿编号,并记录对应编号岛屿的面积
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) isAllGrid = false;
if (!visited[i][j] && grid[i][j] == 1) {
count = 0;
dfs(grid, visited, i, j, signals);
gridNum[signals] = count;
signals++;
}
}
}
// 全部为陆地的情况
if (isAllGrid == true) {
cout << n * m << endl;
return 0;
}
// 遍历海洋变为陆地
unordered_set<int> visitedGrid; // 记录加过的岛屿
int counts = 0;
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 0) {
counts = 1;
visitedGrid.clear();
for (int k = 0; k < 4; k++) {
int curx = i + dir[k][0];
int cury = j + dir[k][1];
if (curx < 0 || curx >= grid.size() || cury < 0 || cury >= grid[0].size()) continue;
if (visitedGrid.count(grid[curx][cury])) continue;
counts += gridNum[grid[curx][cury]];
visitedGrid.insert(grid[curx][cury]);
}
result = max(result, counts);
}
}
}
cout << result << endl;
return 0;
}
8. 岛屿的周长
106. 岛屿的周长
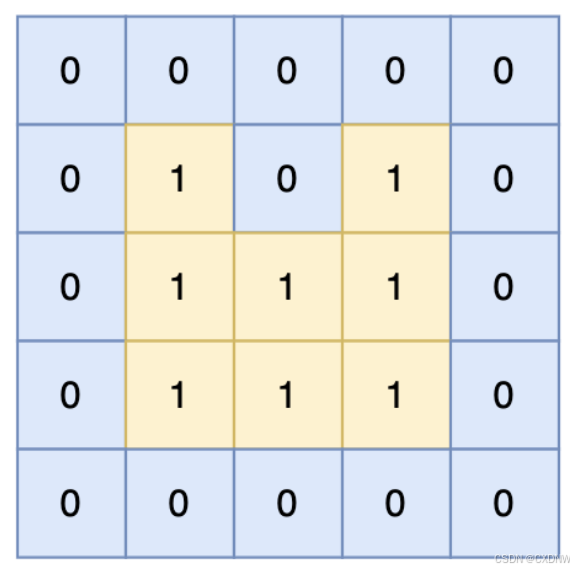
给定一个由 1(陆地)和 0(水)组成的矩阵,岛屿是被水包围,并且通过水平方向或垂直方向上相邻的陆地连接而成的。
你可以假设矩阵外均被水包围。在矩阵中恰好拥有一个岛屿,假设组成岛屿的陆地边长都为 1,请计算岛屿的周长。岛屿内部没有水域。
输入描述
第一行包含两个整数 N, M,表示矩阵的行数和列数。之后 N 行,每行包含 M 个数字,数字为 1 或者 0,表示岛屿的单元格。
输出描述
输出一个整数,表示岛屿的周长。输入示例
5 5
0 0 0 0 0
0 1 0 1 0
0 1 1 1 0
0 1 1 1 0
0 0 0 0 0输出示例
14// 写法一:
#include <iostream>
#include <vector>
using namespace std;
int count = 0;
int dir[4][2] = {1, 0, -1, 0, 0, 1, 0, -1};
void bfs(const vector<vector<int>>& grid, vector<vector<bool>>& visited, int x, int y) {
if (grid[x][y] == 0) {
return;
}
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()
|| grid[nextx][nexty] == 0) {
count++;
continue;
}
if (!visited[nextx][nexty]) {
visited[nextx][nexty] = true;
bfs(grid, visited, nextx, nexty);
}
}
}
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
vector<vector<bool>> visited(n, vector<bool>(m, false));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == 1) {
visited[i][j] = true;
bfs(grid, visited, i, j);
}
}
}
cout << count << endl;
return 0;
}
// 写法二:
#include <iostream>
#include <vector>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> grid(n, vector<int>(m, 0));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> grid[i][j];
}
}
int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};
int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (grid[i][j] == 1) {
for (int k = 0; k < 4; k++) {
int x = i + direction[k][0];
int y = j + direction[k][1];
if (x < 0 || x >= grid.size()
|| y < 0 || y >= grid[0].size()
|| grid[x][y] == 0) {
result++;
}
}
}
}
}
cout << result << endl;
return 0;
}