一、什么是岭回归
岭回归(Ridge Regression),也称为Tikhonov正则化(Tikhonov Regularization),是一种专门用于处理多重共线性(特征之间高度相关)问题的线性回归改进算法,显然它是一个回归模型。在多重共线性的情况下,数据矩阵可能不是满秩的,这意味着矩阵不可逆,因此不能直接使用普通最小二乘法(Ordinary Least Squares,OLS)来估计模型参数。岭回归通过在损失函数中添加一个正则化项(惩罚项)来解决这个问题。
二、岭回归模型建模流程
1、定义损失函数
岭回归的损失函数是残差平方和(RSS)与正则化项的和。残差平方和是模型预测值与实际值之差的平方和,而正则化项是模型参数的L2范数(平方和)。岭回归的损失函数可以表示为:
其中,n是样本数量,m是特征数量,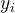
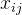
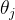

正则化项的作用是惩罚模型参数的大小。当
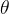

2、构建设计矩阵
设计矩阵X是一个n×m的矩阵,其中每一行代表一个样本,每一列代表一个特征。通常在设计矩阵中加入一列值为1的偏置项,以便模型包含截距项。
3、参数估计
岭回归的参数估计可以通过最小化损失函数来实现。由于损失函数是二次的,因此可以通过解析方法直接求解(比梯度下降更方便)。具体来说,岭回归的参数可以通过以下公式计算得到:
其中,X是设计矩阵,y是目标值向量,
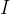
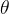
可能会遇到数值稳定性问题,尤其是当
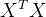
4、模型评估
参数被计算出来之后,就可以使用它们来对新数据进行预测,并评估模型的性能。通常使用均方误差(MSE)或决定系数(R²)等指标来评估模型。
5、超参数选择
正则化参数

三、模型应用
这里使用经典的波士顿房价数据进行回归建模。
# 导入必要的库
from sklearn.datasets import load_boston
from sklearn.linear_model import Ridge
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
# 加载波士顿房价数据集
boston = load_boston()
X, y = boston.data, boston.target
# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建岭回归模型实例,设置正则化参数alpha(就是公式中的λ)
ridge_reg = Ridge(alpha=1.0)
# 训练模型
ridge_reg.fit(X_train, y_train)
# 在测试集上进行预测
y_pred = ridge_reg.predict(X_test)
# 计算均方误差(MSE)
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse:.2f}')
# 可选:打印模型参数
print(f'Model coefficients: {ridge_reg.coef_}')
print(f'Model intercept: {ridge_reg.intercept_}')四、总结
岭回归模型是很简单的机器学习模型,但也是很常见的baseline模型,尤其是在数据特征数量多于样本数量,或者特征之间存在高度相关性的情况下,我们会倾向于先用岭回归建模看看效果。模型具体的优缺点如下:
1、优点
(1)处理多重共线性:岭回归能够有效处理特征之间的高度相关性,提高模型的稳定性。
(2)泛化能力:通过正则化减少模型的复杂度,降低过拟合的风险。
(3)参数解释性:岭回归的参数估计具有较好的解释性,可以用于统计推断。
2、缺点
(1)正则化参数的选择:需要选择合适的正则化参数,这需要依赖经验或者交叉验证。

