题目1:计算聚类中心点并对图像进行重构
代码:
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from skimage import io
def find_data_type(X, centers):
idx = []# 聚类中心和样本点不再变化后每个样本点的的类
for i in range(len(X)):
distance = np.linalg.norm((X[i] - centers), axis=1)
id_i = np.argmin(distance)
idx.append(id_i)
return np.array(idx)
def calculate_center_type(X, idx, k):
centers = []
for i in range(k):
centers_i = np.mean(X[idx == i], axis=0)# 按行求均值
centers.append(centers_i)
return np.array(centers)
def kmeans(X, centers, iters):
k = len(centers)
centers_all = []# 观察聚类中心移动轨迹
centers_all.append((centers))
centers_i = centers
for i in range(iters):
idx = find_data_type(X, centers_i)
centers_i = calculate_center_type(X, idx, k)
centers_all.append(centers_i)
return idx, np.array(centers_all)
def plot_data(X, centers_all, idx):
plt.figure()
plt.scatter(X[:, 0], X[:, 1], c=idx, cmap='rainbow')
plt.plot(centers_all[:, :, 0], centers_all[:, :, 1], 'kx--')# centers_all返回三维数组,第一个是迭代次数,第二个是类别数,第三个是特征数
def init_centers(X,k):#从数据集中随机选取成为聚类中心点
index = np.random.choice(len(X), k)
return X[index]
data1 = sio.loadmat('./data/ex7data2.mat')
print(data1.keys())
X = data1['X']
print(X.shape)
plt.scatter(X[:, 0], X[:, 1])
plt.show()
centers = np.array([[3, 3], [6, 2], [8, 5]])
idx = find_data_type(X, centers)
print(idx[:3])
centers_location = calculate_center_type(X, idx, k=3)
print(centers_location)
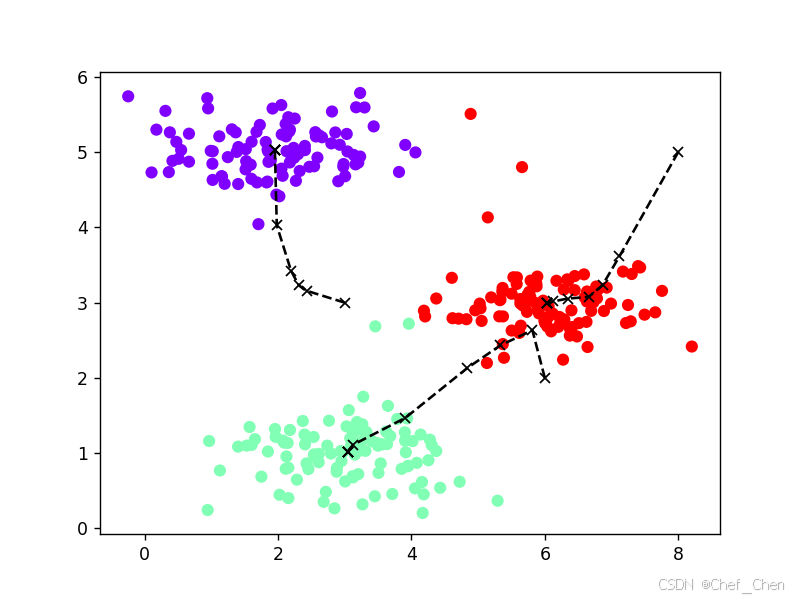
idx, centers_all = kmeans(X, centers, iters=10)
plot_data(X, centers_all, idx)
plt.show()
data2 = sio.loadmat('./data/bird_small.mat')
print(data2.keys())
A = data2['A']
print(A.shape)
image = io.imread('./data/bird_small.png')
plt.imshow(image)
plt.axis('off') # 关闭坐标轴
plt.show()
A = A/255 #标准化
A = A.reshape(-1, 3) # -1表示对行没有要求,系统自动匹配
k=16
idx, centers_all = kmeans(A, init_centers(A, k=16), iters=10)
centers = centers_all[-1]
im = np.zeros(A.shape)
for i in range(k):# 获取当前类的所有样本点
im[idx==i] = centers[i]
im = im.reshape(128, 128, 3)
plt.imshow(im)
plt.axis('off')
plt.show()输出:
dict_keys(['__header__', '__version__', '__globals__', 'X'])
(300, 2)
[0 2 1]
[[2.42830111 3.15792418]
[5.81350331 2.63365645]
[7.11938687 3.6166844 ]]
dict_keys(['__header__', '__version__', '__globals__', 'A'])
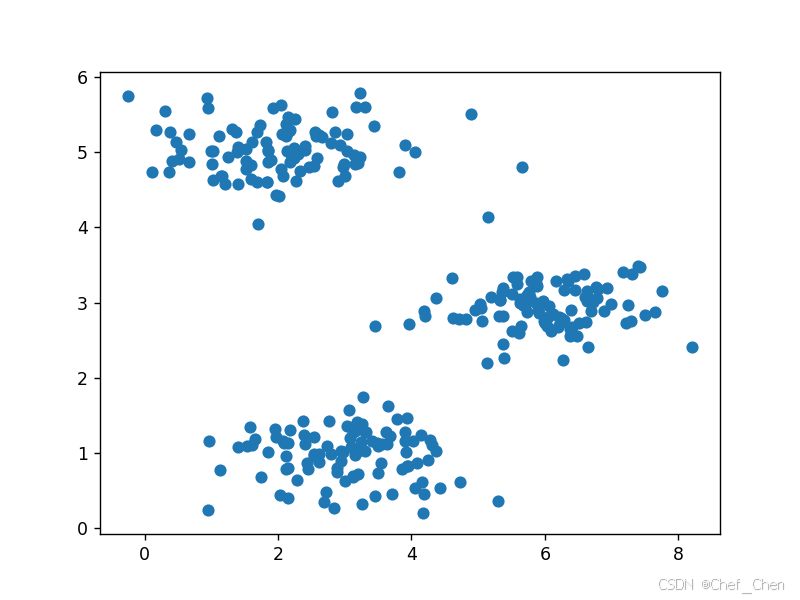
(128, 128, 3)原始数据散点图
对数据进行去均值化处理
原始子图
降维后的子图
题目2:对二维数据进行降维
代码:
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
mat = sio.loadmat('./data/ex7data1.mat')
print(mat.keys())
X = mat['X']
print(X.shape)
plt.scatter(X[:, 0], X[:, 1])
plt.show()
X_demean = X - np.mean(X, axis=0) #去均值化,新的样本均值为0, 看起来符合高斯分布(也就是正态分布)
plt.scatter(X_demean[:, 0], X_demean[:, 1])
plt.show()
C = X_demean.T@X_demean / len(X)# 求协方差矩阵
print(C)
U, S, V = np.linalg.svd(C)
print(U)
print(S)
print(V)
U1 = U[:, 0]# 由于是降为一维,所以取得是第一项
X_reduction = X_demean@U1
X_restore = X_reduction.reshape(50, 1)@U1.reshape(1, 2) + np.mean(X, axis=0)#之前做了去均值化操作,为了显示要加回来
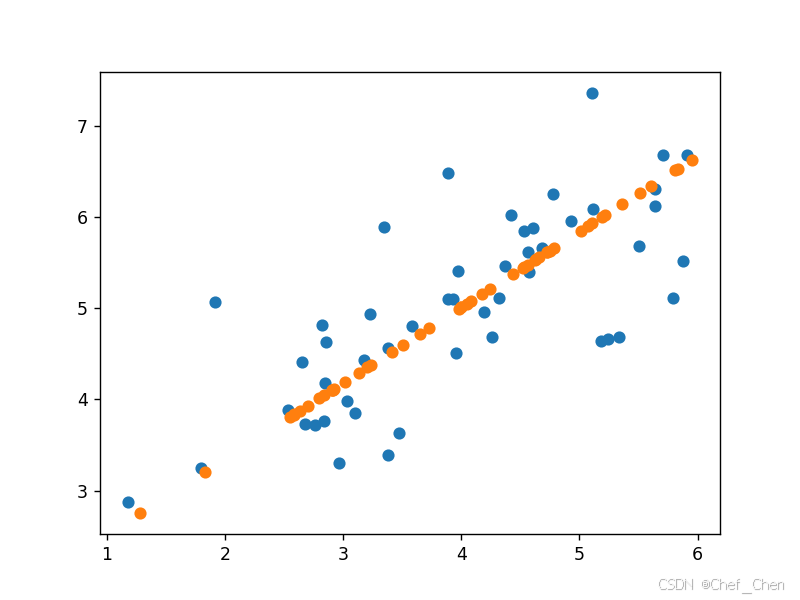
plt.scatter(X[:, 0], X[:, 1])
plt.scatter(X_restore[:, 0], X_restore[:, 1])
plt.show()输出:
dict_keys(['__header__', '__version__', '__globals__', 'X'])
(50, 2)
[[1.34852518 0.86535019]
[0.86535019 1.02641621]]
[[-0.76908153 -0.63915068]
[-0.63915068 0.76908153]]
[2.06768062 0.30726078]
[[-0.76908153 -0.63915068]
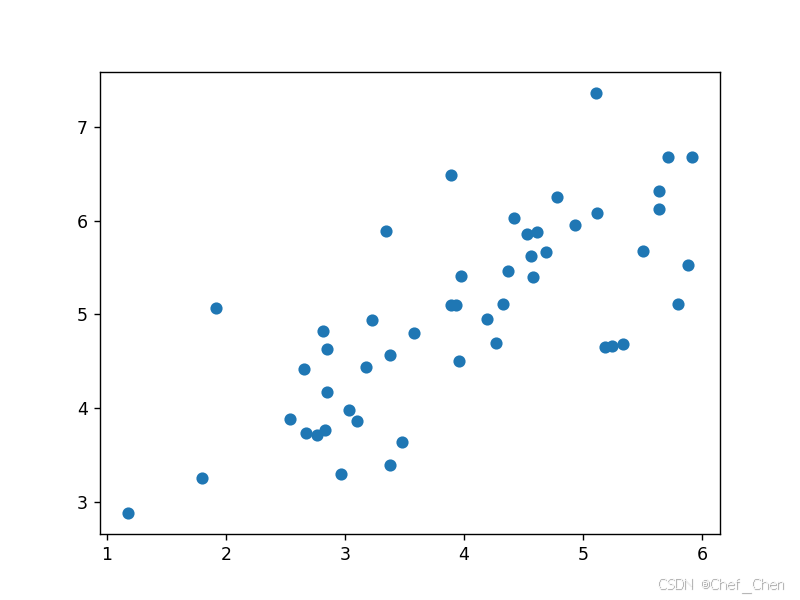
[-0.63915068 0.76908153]]原始数据散点图
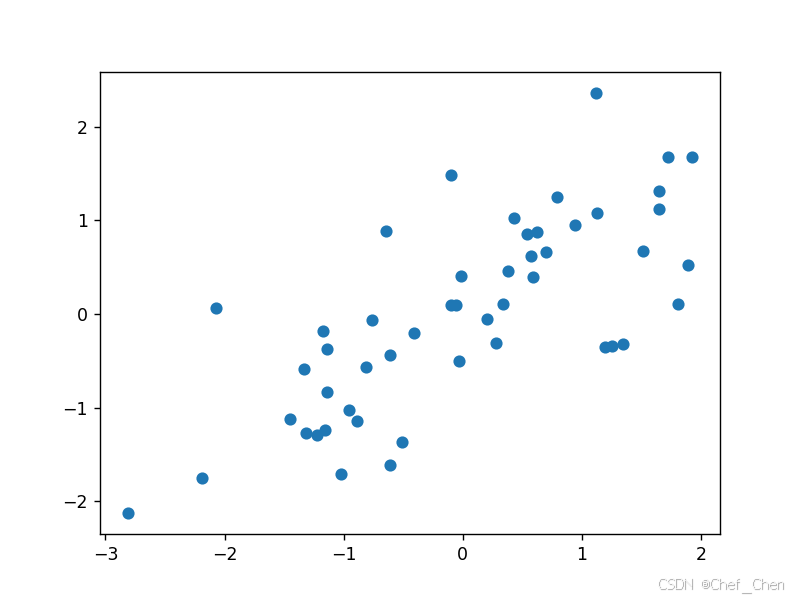
对数据进行去均值化处理
降维又重构的数据与原始数据对比
题目3:对图片进行降维
代码:
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
def image(X):
fig, axs = plt.subplots(ncols=10, nrows=10, figsize=(10, 10))
for c in range(10):
for r in range(10):
axs[c, r].imshow(X[10*c + r].reshape(32, 32).T, cmap = 'Greys_r')# 转成32×32的数组再转置是为了使其适应imshow,能够导出子图
axs[c, r].set_xticks([])
axs[c, r].set_yticks([])
mat = sio.loadmat('./data/ex7faces.mat')
print(mat.keys())
X = mat['X']
print(X.shape)
image(X)
plt.show()
means = np.mean(X, axis=0)
X_demean = X-means
C = X_demean.T@X_demean
U, S, V = np.linalg.svd(C)
U1 = U[:, : 36]
X_reduction = X_demean@U1
print(X_reduction.shape)
X_recover = [email protected] + means
image(X_recover), image(X)
plt.show()输出:
dict_keys(['__header__', '__version__', '__globals__', 'X'])
(5000, 1024)
(5000, 36)原始子图
降维后的子图
小结:与之前相比,此次作业加深了对于数据预处理的重要性,希望在后面建立粗略模型时能先把数据预处理的细节打磨一下,方便后面整体建模。