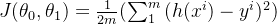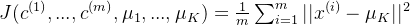一、机器学习是什么

为计算机开发的一种功能，采用学习算法使其模拟人类大脑的学习方式，从而实现各种各样的能力，如网站搜索，图片推荐，清理垃圾邮件等等。

监督学习

定义：给定算法一个数据集，其中包含了正确答案，而我们想要算法通过这个来输出更多数据的正确答案。

算法：

• 线性回归：处理两个变量的问题，输出为常数，常见有求利润、面积、房价等；

• 逻辑回归：处理分类问题，输出为概率，常见有垃圾分类、清理垃圾邮件、图片分类等；

• 支持向量机（SVM）：常用于处理分类问题，输出为预测结果，即0或1，常见有文字识别、人脸识别等。

非监督学习

定义：给定算法一个无标签的数据集，让算法自行判断需要对数据集做什么处理。

算法：

• K-means算法：处理聚类问题，输出为概率，常见有数据预处理中的降维或图像分割等；

• 主成分分析算法（PCA）：一般用于数据降维或者对数据进行可视化，方便分析；

• 推荐算法：基于内容选择更合适的特征，通过学习同时调整参数和特征，输出为常数值，常见有视频推送、预测电影预售利润等。

深度学习

定义：通过多个层次的非线性处理单元对数据和特征进行转换。

算法：

• 神经网络：处理复杂的非线性问题，输出取决于解决什么问题，常见有预测分类以及图像处理等。

二、模型构建

数据预处理

• 数据清洗：处理缺失值、异常值、重复数据，对数据进行随机初始化等；

• 数据变换：对数据进行归一化、标准化或降维等；

• 特征提取：选择或创造对模型可能有用的特征量。

算法选择

根据问题的性质和数据特性，判断属于哪种问题，进而选择合适的学习算法。

代价函数选择

• 线性回归：
• 逻辑回归：
• 支持向量机（SVM）：
• K-means：
• 神经网络：
• 推荐算法：

训练过程

一般会将数据集分为训练集、验证集以及测试集，分配比例为6:2:2。

• 训练集:通过训练来调整用于最小化损失函数的参数；

• 验证集:用于选择在训练集中训练出的最佳参数、防止过拟合；

• 测试集:用于测试模型训练好的参数和特征，判断算法是否有效解决问题。

三、模型评估

• 准确率：计算公式为（预测正确的样本数）/（总样本数），在正常数据中是一个很好的评估指标，但在不正常（如偏斜类）问题中会被数据误导；

• 召回率：计算公式为（预测正确的正例数）/（实际正例数），由于关注的是真实值为真的样本，在偏斜类问题一般用召回率来判断模型好坏；

• F1分数：计算公式为2 ×（准确率 × 召回率）/（准确率 + 召回率），由于同时考虑准确率和召回率，是一个更加平衡、客观的评估指标。

四、模型优化

• 学习曲线：通过观察训练集和验证集的代价函数值随着样本数量的变化，来判断属于高偏差还是高方差问题，从而做出有用的优化。

• 超参数调优：用于辅助寻找最小化代价函数的最佳参数，常见的是用梯度下降法，但一般寻找到的是局部最优解而不是全局最优解；

• 正则化：用于筛选对模型有用的特征变量，防止出现或欠拟合过拟合问题；

• 异常检测：标记处分类问题中可能会有的特殊样本，防止其干扰算法结果。