前言
在学习框架源码底层时,有非常多的二进制运算,由于大学学习计算机基础时开小差,没有学习牢固,所以在看底层源码的算法逻辑时遇到二进制运算比较吃力,遂通过一篇博文来总结下二进制运算,记录一下。
读者认真阅读完整片文章,看完如果还不懂可以来砍我~
正文
1. 二进制基础
因为计算机底层是通过二进制来进行计算的,所以在计算机底层会将十进制转换为二进制。十进制就是逢10进1,二进制就是逢2进1。
就十进制来说,比如一百可以分为三位,个位、十位、百位, 用位数在下列表示 101这个十进制数。
| 百位 | 十位 | 十位 |
|---|---|---|
| 1 | 0 | 1 |
因此对于十进制来说,越往上进制位越大,比如千位、万位。
同理,对于二进制来说也有对应位数, 如果表示二进制的4。
| 4(2^2) | 2(2^1) | 1(2^0) |
|---|---|---|
| 1 | 0 | 0 |
1 * 4 + 2 * 0 + 1 * 0 = 4
如果要表示二进制的5,则如下图
| 4(2^2) | 2(2^1) | 1(2^0) |
|---|---|---|
| 1 | 0 | 1 |
4 * 1 + 2 * 0 + 1 * 1 = 5
如果要表示二进制的11,则如下图
| 8(2^3) | 4(2^2) | 2(2^1) | 1(2^0) |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
8 * 1 + 4 * 0 + 2 * 1 + 1 * 1 = 11
在计算机中,1字节有8位二进制位。
2. 二进制运算
在计算机系统中,二进制运算包括了二进制逻辑运算和二进制算术运算,而逻辑运算和算术运算的主要区别在于,逻辑运算是按位进行,不像算术运算中位与位之间有进位和借位的联系。下面介绍的与、或、异运算就属于二进制的逻辑运算。
2.1 二进制逻辑运算
对于二进制的逻辑运算,记住一个口诀:
-
与(&)运算
运算规则:
0&0=0, 0&1=0, 1&0=0, 1&1=1二者为1则为1,否则都为0。
-
或(|)运算
运算规则:
0|0=0,0|1=1,1|0=1,1|1=1遇1则1,否则为0。
-
异(^)或运算
运算规则:
0^0=0, 1^0=1, 0^1=1, 1^1=0同为0,异为1。
由于算术运算中会设计符号数的运算,所以先介绍二进制中的源码、补码以及反码。
2.2 二进制算术运算
在二进制算术运算中,包括加、减、乘、除。
加法
0 + 0 = 1
1 + 1 = 10
1 + 0 = 1
0 + 1 = 1
乘法
0 × 0 = 0
1 × 0 = 0
0 × 1 = 0
1 × 1 = 1
减法
0-0=0
1-0=1
1-1=0
0-1=1
除法
0÷1=0
1÷1=1
3. 二进制的源码、补码以及反码
二进制源码是什么?
由于数字有正负之分,所以在计算机中通过在一个数的二进制的最高位存放符号(0为正,1为负),而其他数值位存放着就是数值的二进制位, 这就是二进制源码。需要知道的是,正数的源码、补码和反码都是一样的。
源码有缺点,就是不能直接进行运算,因为运算会出错。源码是有符号数的最简单的编码方式,便于输入输出,但作为代码加减运算时较为复杂。
二进制反码是什么?
反码通常是用来由源码求补码或者由补码求源码的过度码,根据定义可以根据补码的整数和小数中"0"的表示形式各有2中,+0和-0不一样。以8位机器数为例,
整数的"+0"源码为:0,0000000,反码为:0,0000000。整数的"-0"源码为:1,0000000,反码为:1,1111111。
反码跟源码是正数时一样,为负数是,除符号位外,其他为所有数值取反。
一句话概括就是,反码是用于计算负数补码的过度码。
二进制补码是什么?
由于数字有正负之分,所以在计算机中通过在一个数的二进制的最高位存放符号(0为正,1为负),而这就是机器数的补码。还需要知道的一点是,在计算机中是负数是以补码的形式存储的,由于正数的源码和补码相同,所以正数以源码或者补码的形式存储在计算机中都是正确的说法,而负数的源码和补码则不相同。二进制运算后,会将补码结果转换为源码之后,再计算其十进制值。
总结起来补码的作用就是:
- 使符号位能与有效值部分一起参加运算,从而简化运算规则.
- 使减法运算转换为加法运算,进一步简化计算机中运算器的线路设计 所有这些转换都是在计算机的最底层进行的,而在我们使用的汇编、C等其他高级语言中使用的都是原码。
源码和反码之间怎么转换?
源码除了最高位的符号位外,其他位数全部取反,得到的就是反码。
补码和反码之间怎么转换?
补码则是在反码的基础上加一。
小结
对于源码、补码和反码,三者均有符号位和数值位两部分,最高位为符号位,其余位均为数值位。符号位用0表示正,1表示负,而数值位三者表示方法都不同。在计算机系统中,数值一律用补码来
表示和存储,原因在于补码可以将符号位和数值域统一处理,同时加法和减法也可以同一处理,此外源码和补码互相转换,其运算过程是相同的,不需要额外的硬件电路。
一个负整数和其补数相加和为模,对一个整数的补码再求补码等于该整数自身,补码的正零与负零表示方法相同。
4. 二进制的移位运算符
在二进制中,移位运算符是一种位操作运算符。移位运算符可以在二进制的基础上对数字进行平移。按照平移的方向和位数填充规则可以将移位运算符分为三种:<<(左移)、>>(有符号右移)和>>>(无符号右移)。
4.1 <<(左移)
<<表示的是左移,将运算数的二进制整体左移指定的位数,低位用0补齐,因此左移不存在有符号和无符号的区别。
例如在java中int类型的十进制数16,由于在java中,int类型占4字节,1字节有8位, 所以其二进制源码表示为:
0000 0000 0000 0000 0000 0000 0001 0000
16 << 2 ,就是相当于将16的二进制数整体左移2为,然后低位补0,移位操作后:
0000 0000 0000 0000 0000 0000 0100 0000
那么我们再来看下对于负数的左移运算。
-16,其二进制源码为:
1000 0000 0000 0000 0000 0000 0001 0000
反码:
1111 1111 1111 1111 1111 1111 1110 1111
补码:
1111 1111 1111 1111 1111 1111 1111 0000
-16 << 2 , 对补码进行向左移2位, 低位补0
1111 1111 1111 1111 1111 1111 1100 0000
由于移位后最高位仍然为1,表示负数,所以需要借助反码来运算
反码为补码 - 1,则结果为:
1111 1111 1111 1111 1111 1111 1011 1111
源码为反码取反,则结果为:
1000 0000 0000 0000 0000 0000 0100 0000
-1 * (2 * 2 ^ 6) = -64
小结:对于左移运算,a << b,相当于 a * 2 ^ b。
4.2 >> (有符号右移)
在计算机中>> 表示有符号右移,就是将二进制整体右移指定位数,如果是正数,则高位用0补齐,如果是负数,则高位用1补齐。
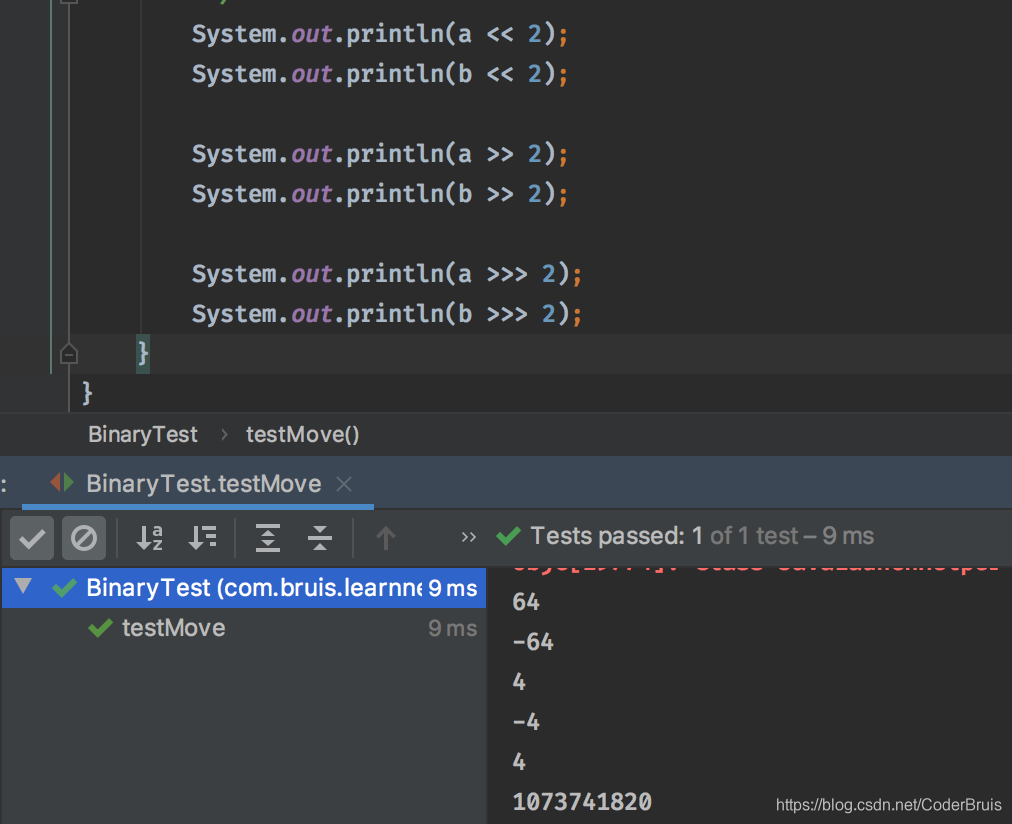
仍然用java中16和-16来进行有符号右移操作,
16 >> 2
通过二进制补码是运算,最终结果为4,同样的-16 >> 2 结果为-4,详细的通过二进制运算结果这里就不展示了,参考左移中列出的详细步骤。
小结:对于有符号右移来说,如果是正数,移动指定位数后,高位用0来补齐;如果是负数,高位用1补齐。
4.3 >>>(无符号右移)
在计算机中通过>>>来表示无符号右移,不管是正数还是负数,高位都用0来补齐。
对于正数,无符号右移>>>和有符号右移>>结果都相同。
同样的用java中16和-16来进行无符号右移运算。
16 >>> 2 结果为 4。
而对于负数来说,无符号右移结果就需要进行计算了。
-16的补码为:
1111 1111 1111 1111 1111 1111 1111 0000
则无符号右移,结果为:
0011 1111 1111 1111 1111 1111 1111 1100
由于正数的源码、补码和反码都一样,所以移位后的源码为:
0011 1111 1111 1111 1111 1111 1111 1100,计算二进制得。
1 * 2 ^ 29 + 1 * 2 ^ 28 + 1 * 2 ^ 27 + 1 * 2 ^ 26 + … + 1 * 2 ^ 2 = 1073741820。
tip 可以通过小技巧来快速计算结果
聪明的读者估计能发现,在二进制位数中,高位的十进制值为其余右边进制之和 + 1,读者可以自行去验证。
所以,
0011 1111 1111 1111 1111 1111 1111 1100
^
取该位置计算得出的十进制值,然后-1,再减去 1 * 2^1 + 1 * 2 ^ 0,即:
2 ^ 30 - 1 - 2 ^ 1 - 2 ^ 0 =1073741824 - 1 - 2 - 1 = 1073741820。
5. 示例
比如变量 a & (-a) 用二进制怎么运算:
10 & (-10)
&是按位与,首先在计算机中数字都是以补码的形式存在的,比如:
int a = 10
+10,它的源码为:
0000 0000 0000 0000 0000 0000 0000 1010
由于正数的源码和补码相同,所以它的补码为:
0000 0000 0000 0000 0000 0000 0000 1010
对于-10,
它的源码为:
0000 0000 0000 0000 0000 0000 1000 1010
它的反码是源码的数值域取反,即:
1111 1111 1111 1111 1111 1111 1111 0101
它的补码是反码+1,即:
1111 1111 1111 1111 1111 1111 1111 0110
由于二进制运算都是用补码来计算的,所以 a & (-a) ,就是:
0000 0000 0000 0000 0000 0000 0000 1010 & 1111 1111 1111 1111 1111 1111 1111 0110 = 0000 0000 0000 0000 0000 0000 0000 0010
对于二进制来说,由于最高位为0,所以可以知道该数为正数,所以源码、补码和反码都一样。
而由于除开最高位符号位外的所有高位都为0,所以可以只看低四位,即0010,换算十进制后为2。
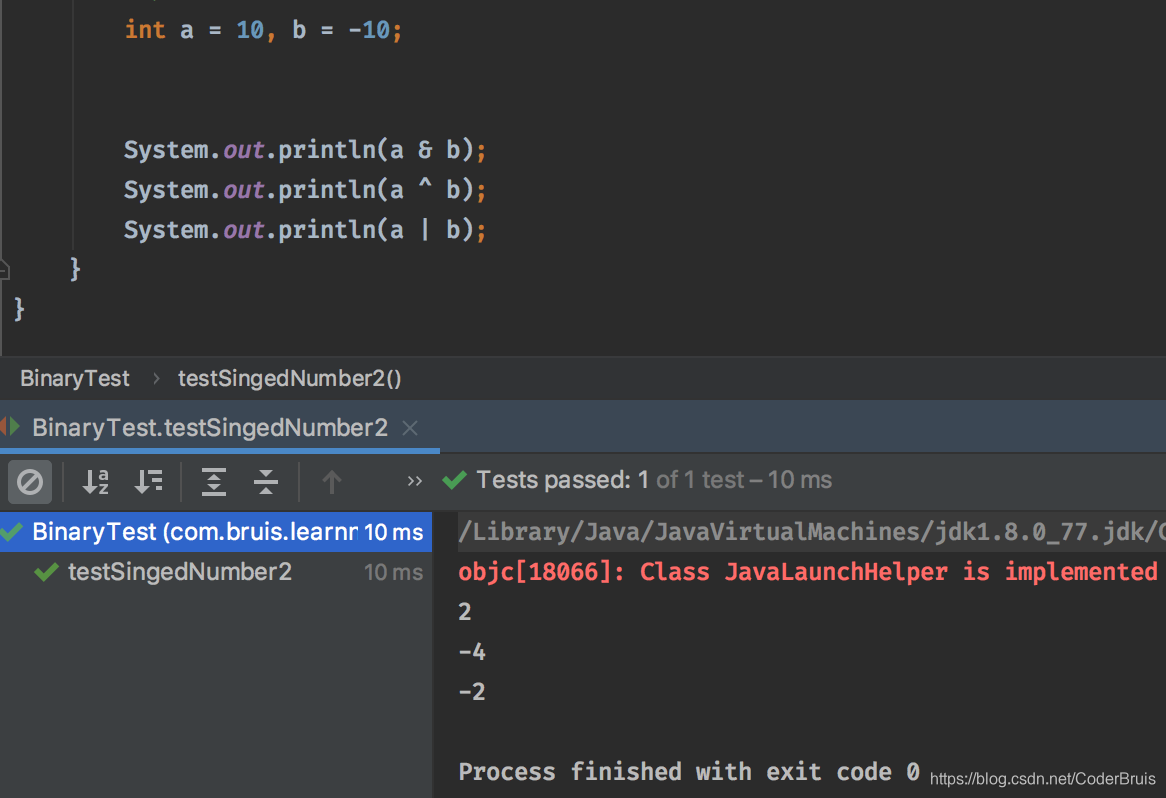
所以如果a=10,则 10 & (-10) = 2。
算完了&,那么再来计算下 ^ 和 | ,看下计算机中是如何通过补码来计算的。
10 ^ (-10)
由于10的补码为:
0000 0000 0000 0000 0000 0000 0000 1010
-10的补码为:
1111 1111 1111 1111 1111 1111 1111 0110
则10 ^ -10 的补码结果为:
1111 1111 1111 1111 1111 1111 1111 1100
由于最高位为1,则该数为负数,需要借助反码来计算其源码。
反码为补码 - 1,则结果为:
1111 1111 1111 1111 1111 1111 1111 1011
源码为反码取反,结果为:
1000 0000 0000 0000 0000 0000 0000 0100
则十进制结果为-4。
10 | (-10)
由于10的补码为:
0000 0000 0000 0000 0000 0000 0000 1010
-10的补码为:
1111 1111 1111 1111 1111 1111 1111 0110
由于最高位为1,则该数为负数,需要借助反码来计算其源码。
则10 | -10 的补码结果为:
1111 1111 1111 1111 1111 1111 1111 1110
反码结果为补码 - 1,则结果为:
1111 1111 1111 1111 1111 1111 1111 1101
源码为反码结果取反,结果为:
1000 0000 0000 0000 0000 0000 0000 0010
计算的十进制结果为 -2。
通过一个简单的示例分析,相信读者已经弄清楚了源码、补码和反码之间的关系以及在二进制运算中是如何运用的了。
在开源框架底层中算法会用到大量的二进制运算, 例如:在最近学习的Netty底层源码中,DefaultEventExecutorChooserFactory的底层源码有一个方法, 就是通过 a & (-a)来运算的。
@Override
public EventExecutorChooser newChooser(EventExecutor[] executors) {
if (isPowerOfTwo(executors.length)) {
return new PowerOfTowEventExecutorChooser(executors);
} else {
return new GenericEventExecutorChooser(executors);
}
}
/*
* 用于计算val是否是2的幂,例如2、4、8、16
*/
private static boolean isPowerOfTwo(int val) {
return (val & -val) == val;
}
private static final class PowerOfTowEventExecutorChooser implements EventExecutorChooser {
private final AtomicInteger idx = new AtomicInteger();
private final EventExecutor[] executors;
PowerOfTowEventExecutorChooser(EventExecutor[] executors) {
this.executors = executors;
}
/*
* 通过二进制与运算计算出下标索引值,原理如下:
* 假设:idx = 2 , 二进制表示为:0000 0010
* executors.length = 16, 则executors.length - 1 = 15, 二进制表示为:0000 1111
*
* 由于是与运算,且executors.length高四位为0000,则只需要注意低四位的运算。
* 则: 0010 & 1111 = 0010 ,十进制表示为2,
*
* 所以如果idx = 3, 则二进制为:0011 & 1111 = 0011 也为3,
* 等idx = 16时,二进制为:0001 0000 & 1111 = 0000 0000 ,即十进制的1,
* 这样就实现了在0 ~ 15 范围内循环获取下标索引的目的。
*/
@Override
public EventExecutor next() {
return executors[idx.getAndIncrement() & executors.length - 1];
}
}
private static final class GenericEventExecutorChooser implements EventExecutorChooser {
private final AtomicInteger idx = new AtomicInteger();
private final EventExecutor[] executors;
GenericEventExecutorChooser(EventExecutor[] executors) {
this.executors = executors;
}
/*
* 通过取余运算,计算出下标索引
*/
@Override
public EventExecutor next() {
return executors[Math.abs(idx.getAndIncrement() % executors.length)];
}
}
总结
在计算机中,二进制的运算是比较重要的,可以看到在Java的许多开源框架底层就运用到了大量的二进制与或非运算,所以学好二进制的基础概念是非常重要的。