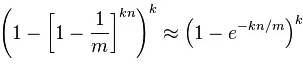布隆过滤器，原理+案例+代码实现

概述

什么是布隆过滤器

布隆过滤器（Bloom Filter）是1970年由布隆提出的，它实际上是由一个很长的二进制向量和一系列随意映射函数组成。

它是一种基于概率的数据结构，主要用来判断某个元素是否在集合内，它具有运行速度快（时间效率），占用内存小的优点（空间效率），但是有一定的误识别率和删除困难的问题。它能够告诉你某个元素一定不在集合内或可能在集合内。

在计算机科学中，我们常常会碰到时间换空间或者空间换时间的情况，通常两者不可兼得，我们要在两者之间取舍。但是布隆过滤器在空间与时间效率上都很高。那么他是怎么做到的？因为Bloom Filter在时间空间这两个因素之外又引入了另一个因素：错误率。在使用Bloom Filter判断一个元素是否属于某个集合时，会有一定的错误率。也就是说，有可能把不属于这个集合的元素误认为属于这个集合（False Positive），但不会把属于这个集合的元素误认为不属于这个集合（False Negative）。在增加了错误率这个因素之后，Bloom Filter通过允许少量的错误来节省大量的存储空间，同时在时间效率上也很好。

概述小结

一个很长的二进制数组（位数组，就是这个数组里只有0和1）
若干个哈希函数
空间效率和查询效率高
不存在漏报（False Negative），即某个元素在某个集合中，肯定能报出来。
可能存在误报（False Positive），即某个元素不在某个集合中，可能也被爆出来。
删除困难

名词解释

False Position

集合里没有某元素，查找结果是有该元素。

也就是误判，这种情况在布隆过滤器中可能会出现。

False Negative

集合里有某元素，查找结果是没有该元素。

也就是少判，这种情况在布隆过滤器中一定不会出现

参数解释

一个Bloom Filter有以下参数：

m	bit数组的宽度（bit数）
n	加入其中的key的数量
k	使用的hash函数的个数

复杂度分析

空间复杂度方面

Bit的长度为m，每次都要执行k个hash函数

Bloom Filter不会动态增长，运行过程中维护的始终只是m位的bitset，所以空间复杂度只有O(m)。

时间复杂度方面

Bloom Filter的插入与属于操作主要都是在计算k个hash，所以都是O(k)。

哈希函数

详细请看https://en.wikipedia.org/wiki/Hash_function

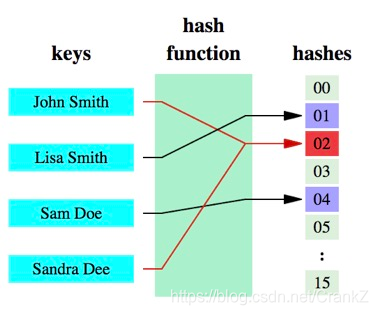
哈希函数的概念是：将任意大小的数据转换成特定大小的数据的函数，转换后的数据称为哈希值或哈希编码。下面是一幅示意图：

可以明显的看到，原始数据经过哈希函数的映射后称为了一个个的哈希编码，数据得到压缩。哈希函数是实现哈希表和布隆过滤器的基础。

哈希函数的性质:

经典的哈希函数都有无限大的输入值域(无穷大)。
经典的哈希函数的输出域都是固定的范围(有穷大，假设输出域为S)
当给哈希函数传入相同的值时，返回值必一样
当给哈希函数传入不同的输入值时，返回值可能一样，也可能不一样。
输入值会尽可能均匀的分布在S上

前三点都是哈希函数的基础，第四点描述了哈希函数存在哈希碰撞的现象，因为输入域无限大，输出域有穷大，这是必然的，输入域中会有不同的值对应到输入域S中。第五点事评价一个哈希函数优劣的关键，哈希函数越优秀，分布就越均匀且与输入值出现的规律无关。比如存在"hash1","hash2","hash3"三个输入值比较类似，经过哈希函数计算后的结果应该相差非常大，可以通过常见的MD5和SHA1算法来验证这些特性。如果一个优秀的函数能够做到不同的输入值所得到的返回值可以均匀的分布在S中，将其返回值对m取余(%m),得到的返回值可以认为也会均匀的分布在0~m-1位置上。

原理分析

以一个例子，来说明添加的过程，这里，假设数组长度m=19，k=2个哈希函数

既然选用hash算法，必然就会存在碰撞的可能。两个不完全相同的值计算出来的hash值难免会一致。多次使用hash算法，为同一个值取不同的多个hash，取的越多。碰撞率的几率就越小。当然hash的数量也不是越多越好，这个后面会讲

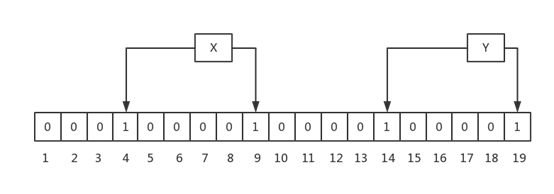
插入数据

如上图，插入了两个元素，X和Y，X的两次hash取模后的值分别为4,9，因此，4和9位被置成1；Y的两次hash取模后的值分别为14和19，因此，14和19位被置成1。

插入流程

将要添加的元素给k个哈希函数
得到对应于位数组上的k个位置
将这k个位置设为1

查找数据

BloomFilter中查找一个元素，会使用和插入过程中相同的k个hash函数，取模后，取出每个bit对应的值，如果所有bit都为1，则返回元素可能存在，否则，返回元素不存在。

查找流程

将要查询的元素给k个哈希函数
得到对应于位数组上的k个位置
如果k个位置有一个为0，则一定不在集合中
如果k个位置全部为1，则可能在集合中

为什么bit全部为1时，元素只是可能存在呢？

当然，如果情况只是上图中，只存在X、Y，而且两个元素hash后的值并不重复。那么这种情况就可以确定元素一定存在。

但是，存在另一种情况。参考上面那个图，假设我们现在要查询Z元素，假设Z元素并不存在。但是巧了经过hash计算出来的位置为9,14。我们很清楚，这里的9是属于X元素的，14是术语Y元素的。并不存在Z。但是经过hash计算的结果返回值都是1。所以程序认为Z是存在的，但实际上Z并不存在，此现象称为false positive

为什么不能删除数据

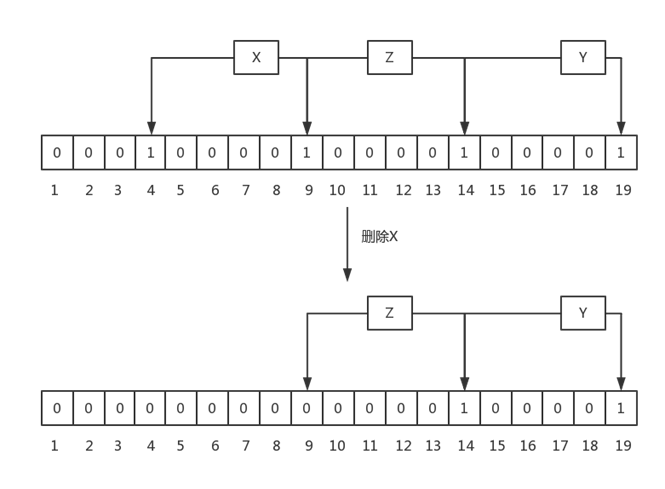
BloomFilter中不允许有删除操作，因为删除后，可能会造成原来存在的元素返回不存在，这个是不允许的，还是以一个例子说明：

上图中，刚开始时，有元素X，Y和Z，其hash的bit如图中所示，当删除X后，会把bit 4和9置成0，这同时会造成查询Z时，报不存在的问题，这对于BloomFilter来讲是不能容忍的，因为它要么返回绝对不存在，要么返回可能存在。

问题：BloomFilter中不允许删除的机制会导致其中的无效元素可能会越来越多，即实际已经在磁盘删除中的元素，但在bloomfilter中还认为可能存在，这会造成越来越多的false positive。

优缺点

优点

相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数（O(k)）。另外, 散列函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。

布隆过滤器可以表示全集，其它任何数据结构都不能；

全量存储但是不存储数据本身，适合有保密要求的场景
空间复杂度为O(m)，不会随着元素增加而增加，占用空间少
插入和查询时间复杂度都是 O(k), 不会随着元素增加而增加，远超一般算法。

缺点

但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。

另外，一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位数组变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。

在降低误算率方面，有不少工作，使得出现了很多布隆过滤器的变种。

存在误算率，数据越多，误算率越高
一般情况下无法从过滤器中删除数据
二进制数组长度和 hash 函数个数确定过程复杂

如何取值（数学原理）

只做简单介绍，详细请看https://en.wikipedia.org/wiki/Bloom_filter

Bloom Filter的原理已经讲完，但还是有必要提一下错误率的问题。错误率有两种：

FP = false positive
FN = false negative

对应Bloom Filter的情况下，FP就是「集合里没有某元素，查找结果是有该元素」，FN就是「集合里有某元素，查找结果是没有该元素」。FN显然总是0，FP会随着Bloom Filter中插入元素的数量而增加——极限情况就是所有bit都为1，这时任何元素都会被认为在集合里。

FP的推导并不复杂，wiki上有非常详细的过程，这里就简单地抄个结果，其中n是当前集合里元素的数量：

FP表达式，截自wiki

从这个公式里可以读出一些直观的信息：

n = 0时，FP = 0；n趋于无穷大时，FP趋于1
k/m和n保持不变时，k越大，FP越小

m和k决定了Bloom Filter的「容量」，当然hash函数的选择也很重要。

使用场景+常用解决方案

如果想判断一个元素是不是在一个集合里，一般想到的是将集合中所有元素保存起来，然后通过比较确定。链表、树、哈希表（Hash table）等等数据结构都是这种思路。但是随着集合中元素的增加，我们需要的存储空间越来越大。同时检索速度也越来越慢，上述三种结构的检索时间复杂度分别为O(n),O(logn),O(n/k)

而布隆过滤器的空间复杂度为O(m)，插入和查询时间复杂度都是O(k)。存储空间和插入、查询时间都不会随元素增加而增大。空间、时间效率都很高！

Tips：m为数组长度。k是哈希函数的数量

为了说明Bloom Filter存在的重要意义，举一个实例：

　　假设要你写一个网络爬虫（web crawler）。由于网络间的链接错综复杂，为了避免重复，就需要知道爬虫已经访问过那些URL。给一个URL，怎样知道爬虫是否已经访问过呢？稍微想想，就会有如下几种方案：

将访问过的URL保存到数据库。
用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了。
URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库。
Bit-Map方法。建立一个BitSet，将每个URL经过一个哈希函数映射到某一位。

　　方法1~3都是将访问过的URL完整保存，方法4则只标记URL的一个映射位。

　　以上方法在数据量较小的情况下都能完美解决问题，但是当数据量变得非常庞大时问题就来了。

　　方法1的缺点：数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询是不是太小题大做了？

　　方法2的缺点：太消耗内存。随着URL的增多，占用的内存会越来越多。就算只有1亿个URL，每个URL只算50个字符，就需要5GB内存。

　　方法3：由于字符串经过MD5处理后的信息摘要长度只有128Bit，SHA-1处理后也只有160Bit，因此方法3比方法2节省了好几倍的内存。

方法4消耗内存是相对较少的，但缺点是单一哈希函数发生冲突的概率太高。若要降低冲突发生的概率到1%，就要将BitSet的长度设置为URL个数的100倍。

其实方案4离布隆过滤器已经很近了，为了避免方法4中冲突率过高的问题。布隆过滤器增加了多个哈希函数。

实战案例：腾讯短视频瀑布流优化

这是布隆过滤器在腾讯短视频实际的应用案例

https://toutiao.io/posts/mtrvsx/preview

简单的讲就是你的每一次刷新都会根据推荐算法推荐你新的内容，但是这个新的内容是不能与已经出现过的内容重复。这时候就需要去重，这时候就可以使用布隆过滤器来去重。

以上这些场景有个共同的问题：如何查看一个东西是否在有大量数据的池子里面。

缓存穿透问题

什么是缓存穿透

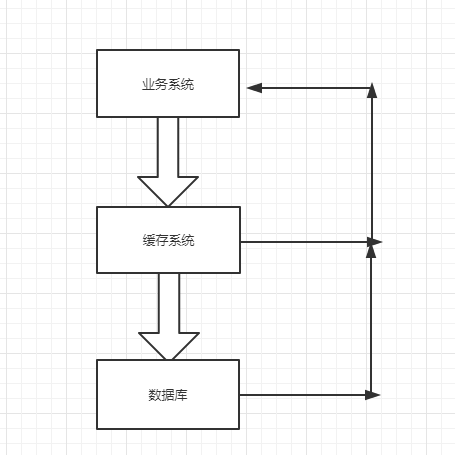
在大多应用中，当业务系统中发送一个请求时，会先从缓存中查询；若缓存中存在，则直接返回；若返回中不存在，则查询数据库。其流程如下图所示:

缓存穿透：当请求数据库中不存在的数据，这时候所有的请求都会打到数据库上，这种情况就是缓存穿透。如果当请求较多的话，这将会严重浪费数据库资源甚至导致数据库假死。

布隆过滤器解决缓存穿透问题

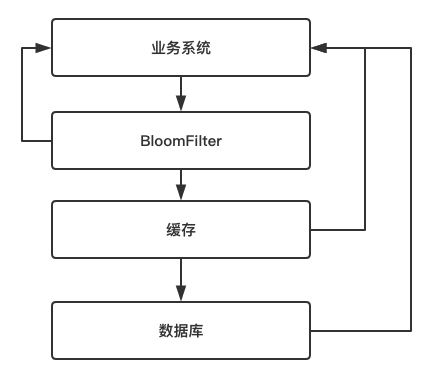
这种技术在缓存之前再加一层屏障，里面存储目前数据库中存在的所有key，如下图

当业务系统有查询请求的时候，首先去BloomFilter中查询该key是否存在。若不存在，则说明数据库中也不存在该数据，因此缓存都不要查了，直接返回null。若存在，则继续执行后续的流程，先前往缓存中查询，缓存中没有的话再前往数据库中的查询。

代码实现布隆过滤器

public class SimpleBloomFilter {
    private static final int DEFAULT_SIZE = 2 << 24;    // 布隆过滤器的比特长度
    private static final int[] seeds = new int[] {7, 11, 13, 31,37, 61};    // 这里要选取质数，能很好的降低错误率

    private BitSet bits = new BitSet(DEFAULT_SIZE);
    private SimpleHash[] func = new SimpleHash[seeds.length];

    public static void main(String[] args) {
        String value = "[email protected]";
        SimpleBloomFilter filter = new SimpleBloomFilter();
        System.out.println(filter.contains(value));
        filter.add(value);
        System.out.println(filter.contains(value));
    }

    public SimpleBloomFilter() {
        for (int i = 0; i < seeds.length; i++) {
            func[i] = new SimpleHash(DEFAULT_SIZE, seeds[i]);
        }
    }

    public void add(String value) {
        for (SimpleHash f: func) {
            bits.set(f.hash(value), true);
        }
    }

    public boolean contains(String value) {
        if (value == null) {
            return false;
        }
        boolean ret = true;
        for (SimpleHash f : func) {
            ret = ret && bits.get(f.hash(value));
        }
        return ret;
    }
    public static class SimpleHash {
        private int cap;
        private int seed;

        public SimpleHash(int cap, int seed) {
            this.cap = cap;
            this.seed = seed;
        }

        public int hash(String value) {
            int result = 0;
            int len = value.length();
            for (int i = 0; i < len; i++) {
                result = seed * result + value.charAt(i);
            }
            return (cap - 1) & result;
        }
    }
}

Google Guava代码

关于布隆过滤器，我们不需要自己实现，谷歌已经帮我们实现好了。

pom引入依赖

<!-- https://mvnrepository.com/artifact/com.google.guava/guava -->
<dependency>
    <groupId>com.google.guava</groupId>
    <artifactId>guava</artifactId>
    <version>27.0.1-jre</version>
</dependency>

代码

guava 的布隆过滤器，封装的非常好，使用起来非常简洁方便。

例：预估数据量1w，错误率需要减小到万分之一。使用如下代码进行创建。

public static void main(String[] args) {
    // 1.创建符合条件的布隆过滤器
    // 预期数据量10000，错误率0.0001
    BloomFilter<CharSequence> bloomFilter =
            BloomFilter.create(Funnels.stringFunnel(
                    Charset.forName("utf-8")),10000, 0.0001);
    // 2.将一部分数据添加进去
    for (int i = 0; i < 5000; i++) {
        bloomFilter.put("" + i);
    }
    System.out.println("数据写入完毕");
    // 3.测试结果
    for (int i = 0; i < 10000; i++) {
        if (bloomFilter.mightContain("" + i)) {
            System.out.println(i + "存在");
        } else {
            System.out.println(i + "不存在");
        }
    }
}