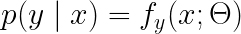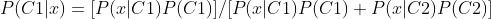贝叶斯方法与朴素贝叶斯
1.生成模型与判别模型
在概率生成模型(Probabilistic Generative Model)与朴素贝叶斯(Naive Bayes)中大概学习了一下概率生成模型以及朴素贝叶斯,今天在这里再总结一下生成模型与判别模型。
上面这张图可以清楚的解释二者的差别。前面我们讲到, 所谓的机器学习模型,本质上是一个函数,其作用是实现从一个样本
x
x
x 到样本的标记值
y
y
y 的映射,即
f
(
x
;
θ
∗
)
→
y
f(x;\theta ^{*})\rightarrow y
f(x;θ∗)→y,或者求得标签的条件概率:
例如有C1以及C2两种类别,我们需要判断样本属于哪一个class:
- 判别式模型:要确定一个样本是属于C1还是C2,用判别模型的方法是从历史数据中学习到模型,然后通过提取该样本的特征来预测出该样本属于C1的概率以及C2的概率。
- 生成式模型:根据C1的特征首先学习出一个C1的模型,然后根据C2的特征学习出一个C2的模型,然后从该样本中提取特征,放到C1模型中看概率是多少,然后再放到C2模型中看概率是多少,哪个大就是哪个。
- 判别模型之所以称为判别模型,就是因为它只是简单地判别就好了。根据样本X来判别它所属的类别,直接就求出了 p ( y ∣ x ) p(y|x) p(y∣x)的大小
- 而生成模型,在概率生成模型(Probabilistic Generative Model)与朴素贝叶斯(Naive Bayes)中我们可以看到,我们要求:
P(C1)与P(C2)很好求,我们要求的是P(x|C1)以及P(x|C2),也就是说我们要先求得C1与C2的具体分布,也就是上面说的,分别根据C1与C2的特征学得两个模型,得到模型之后代入,若P(C1|x)>P(C2|x)那x就属于C1,否则属于C2。
2.贝叶斯
2.1贝叶斯公式
学过概率论的都应该对上面这个公式很熟悉,这里就不再细讲了。这里需要注意的点是注意区分先验概率、后验概率、联合概率三个概念。
2.2贝叶斯方法
机器学习的最终目的就是回归 or 分类,这里二者都可以理解为预测,回归很好理解,分类也可以理解为预测属于某一类的概率是多少。 我们把上述贝叶斯公式中的X理解为“具有某特征”,把Y理解成“类别标签”,那么贝叶斯公式就可以表示为:
P(“属于某类”|“具有某特征”)=P(“具有某特征”|“属于某类”)P(“属于某类”)/P(“具有某特征”)。
贝叶斯方法把计算“具有某特征条件下属于某类(就是分类)”的概率转化为需要计算“属于某类条件下具有某特征(分别训练模型)”的概率,属于有监督学习。
3朴素贝叶斯
我们以垃圾邮件识别来引出朴素贝叶斯。
我们要做的是判断上面那个邮件:“我司可办理正规发票(保真)17%增值税发票点数优惠”是否属于垃圾邮件。我们不能直接判断一整个邮件是否属于垃圾邮件,我们首先想到的应该是“分词”,所谓分词就是把邮件拆成一个个的词语,通过该词语是否属于训练样本中的垃圾邮件来做出进一步判断:
前面我们提到:
贝叶斯方法把计算“具有某特征条件下属于某类(就是分类)”的概率转化为需要计算“属于某类条件下具有某特征(分别训练模型)”的概率,属于有监督学习。 也就是说,我们现在要计算的是:正常邮件 or 垃圾邮件中具有上述那些词语的概率。
3.1条件独立性假设
引入条件独立假设:
我们把求某一类邮件中包含上述那些词语的概率等同于某一类邮件中包含每一种词语概率的乘积!!这其实就是朴素贝叶斯的实质,也是条件独立假设的实质。
既然如此,那每一项都变得特别好求解了:
要算P(x1|C),那就直接在训练集中统计一下,看看x1在类别c1中出现的概率是多少即可。
3.2朴素贝叶斯Naive在何处?
- 加上条件独立假设的贝叶斯方法就是朴素贝叶斯方法(Naive Bayes)
- 由于乘法交换律,朴素贝叶斯中算出来交换词语顺序的条件概率完全一样
上述2的意思是:对于朴素贝叶斯模型来讲,“我司可办理正规发票”与“正规发票可办理我司”是一样的,会给出相同的判别结果,这点应该很好理解,因为你有了条件独立假设, a ∗ b ∗ c a*b*c a∗b∗c与 c ∗ b ∗ a c*b*a c∗b∗a肯定大小是一样的,自然概率也是一样的,判别结果也就一样了。
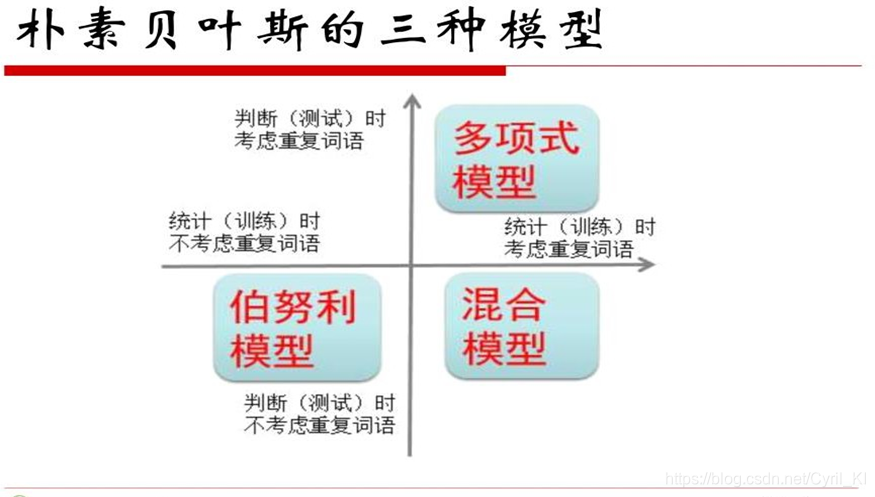
3.3朴素贝叶斯的三种模型
-
多项式模型
多项式模型跟我们思维是一样的,例如在上述条件概率中,“发票”一词语出现了三次,那利用条件独立假设条件之后,自然应该出现三次方,这就是多项式模型。 -
伯努利模型
在伯努利模型中我们可以看到,即使“发票”一词出现三次,但是我们在最终计算时只算一次。 -
混合模型
在混合模型中,我们计算句子概率时不考虑重复词语出现的次数,但在统计计算词语概率时考虑重复次数。
一张图概括三种模型:
3.4平滑技术
我们先来看这样一种可能:我们在求P(“正规发票”|S)时,通常的做法就是在训练集中遍历,看看“正规发票”一词出现了多少次,但是好巧不巧,该词在训练集中一次都没有出现过,那概率不就是0了么,然后条件独立假设相乘。。。于是整个概率都变成了0,这显然是极不合理的,但是这种情况却不少见。
于是我们引入了平滑技术这一概念来解决这个问题:
这样,上述概率就不为0了,方便后续判断。
3.5朴素贝叶斯优缺点
优点:
- 对待预测样本进行预测,过程简单速度快
- 对于多分类问题也同样有效,复杂度也不会有大程度地上升。
- 在分布独立这个假设成立的情况下,贝叶斯的分类效果很好,会略胜于逻辑回归,我们需要的样本量也更少一点。
- 对于类别类的输入特征变量,效果非常好。对于数值型变量特征,我们默认它符合正态分布。
缺点:
- 如果测试集中的一个类别变量特征在训练集里面没有出现过,那么概率就是0,预测功能就将失效,平滑技术可以解决这个问题
- 朴素贝叶斯中有分布独立的假设前提,但是在现实生活中,这个条件很难满足。
3.6朴素贝叶斯的应用与代码实现
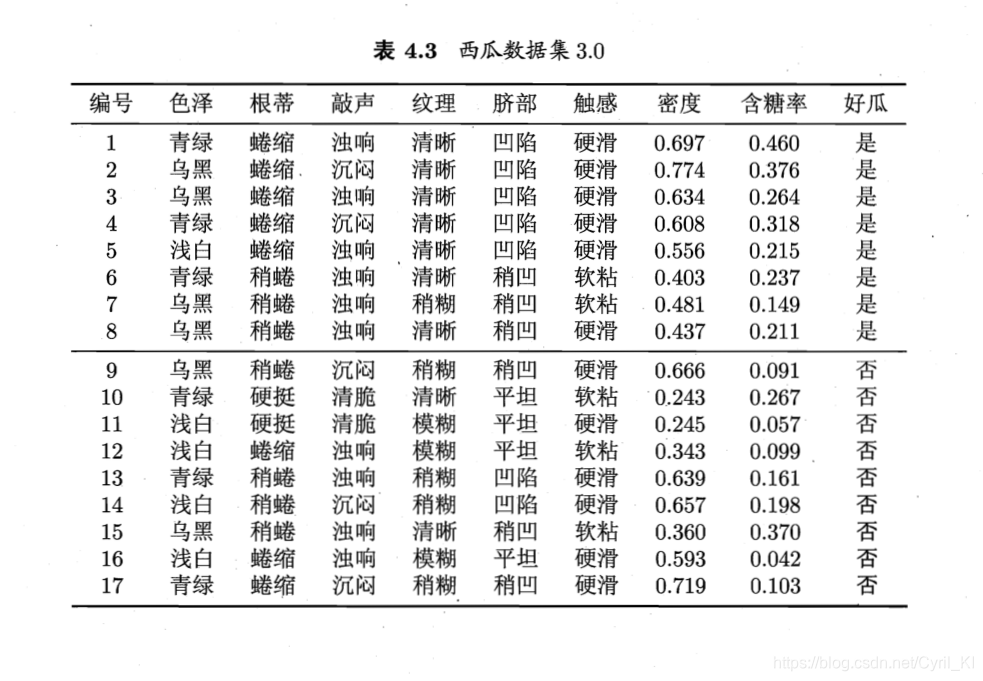
作业:编程实现拉普拉斯修正的朴素贝叶斯分类器,并以西瓜数据集3.0为训练集,对“测1”样本进行判别。
数据集长这样:
代码实现:
import pandas as pd
def readfile():
datasets = pd.read_csv(r'E:\Program Files\PyCharm 2019.2\machinelearning\homework\西瓜3.0.csv', encoding="gbk")
del datasets['编号']
del datasets['好瓜']
return datasets
def NaiveBayes(test):
data = readfile()
data = data.values.tolist()
goodMelon = [];badMelon = []
for i in range(len(data)):
if data[i][8] == 1:
goodMelon.append(data[i])
else:
badMelon.append(data[i])
# 计算p(x|C1)=p1与p(x|C2)=p2
p1 = 1.0;p2 = 1.0
for j in range(len(test)):
x=0.0
for k in range(len(goodMelon)):
if goodMelon[k][j] == test[j]:
x = x + 1.0
p1 = p1 * ((x + 1.0) / (len(goodMelon) + 2.0)) # 拉普拉斯平滑
for j in range(len(test)):
x=0.0
for k in range(len(badMelon)):
if badMelon[k][j] == test[j]:
x = x + 1.0
p2 = p2 * ((x + 1.0) / (len(badMelon) + 2.0)) # 拉普拉斯平滑
pc1 = len(goodMelon) / len(data)
pc2 = 1 - pc1
#贝叶斯公式
p_good = p1*pc1;p_bad=p2*pc2
if p_good > p_bad:
print('好瓜')
else:
print('坏瓜')
if __name__ == '__main__':
test=['青绿','蜷缩','浊响','清晰','凹陷','硬滑',0.697,0.460]
NaiveBayes(test)
结果:好瓜,分类正确。