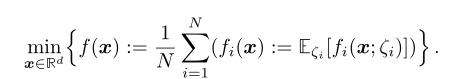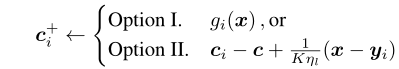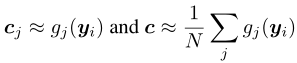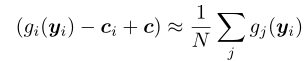前言

题目： SCAFFOLD: Stochastic Controlled Averaging for Federated Learning
会议： International Conference on Machine Learning 2020
论文地址：SCAFFOLD: Stochastic Controlled Averaging for Federated Learning

当客户端数据是非独立同分布时，FedAvg的收敛速度会受到所谓client-drift的影响。作为一种解决方案，本文作者提出了SCAFFOLD，该算法使用控制变量（方差缩减）来纠正其局部更新中的client-drift。

client-drift在之前的一篇文章MLSys 2020 | FedProx：异质网络的联邦优化
中实际上已经提到过了：如果数据是独立同分布的，那么本地模型训练较多的epoch会加快全局模型的收敛；如果不是独立同分布的，不同设备在利用非IID的本地数据进行训练并且训练轮数较大时，本地模型将会偏离初始的全局模型。

我们不妨对FedAvg进行分析（非独立同分布）：

假设一共两个客户端，每个客户端的本地更新次数为3。

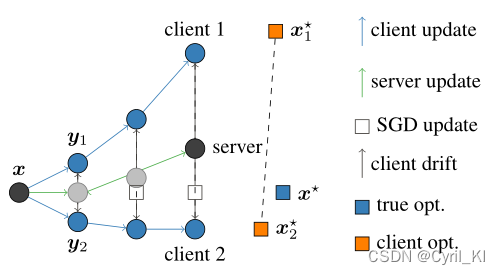
初始的全局模型$x$发送给两个客户端以形成它们的本地模型$y_1$和$y_2$，然后经过三次更新，客户端1的$y_1$向其最优解$x_1^{\ast }$移动，客户端2的$y_2$向其最优解$x_2^{\ast }$移动。之所以两个模型向着两个不同方向移动，是因为两个客户端的数据分布不一致。

两个客户端的三次本地更新完毕后，取两个客户端模型的均值形成最新的server模型。这时的server模型并不在最优解的位置$x^{\ast }$。因此我们可以发现，如果客户端数据分布不一致，那么本地模型在更新时会朝着不同方向进行优化，这会使得我们很难得到一个普适的全局模型。

为了缓解client-drift，本文作者提出了一种新的联邦优化算法SCAFFOLD，SCAFFOLD引入了服务器控制变量$c$和客户端控制变量$c_i$，控制变量中含有模型的更新方向信息，通过在本地模型的更新公式中添加一个修正项$c-c_i$，SCAFFOLD克服了梯度差异，有效缓解了client-drift。

1. 引言

联邦优化存在以下关键挑战：

1. 服务器与客户端间网络连接相对较慢。
2. 在给定时间内只有一小部分客户端能够用于训练。
3. 不同客户端间数据分布的异质性。

FedAvg虽然可以缓解通信压力，但它在异质数据上的表现不太好，如何改正FedAvg的这种缺陷也是联邦学习目前比较热门的一个研究方向。客户端间数据的异质性会在客户端的更新中引入一个client-drift，这会导致收敛变缓。

作为一种解决方案，SCAFFOLD试图纠正这种client-drift。

2. 问题定义

符号定义：

需要优化的函数：

$f_i$表示客户端$i$的损失函数，即最小化所有客户端的平均损失。

3. FedAvg

客户端抽样集合为$S$，对每个被抽样的客户端，其本地模型$y_i=x$将执行$K$次本地更新：
$$y_i\leftarrow y_i-{\eta }_l{g}_i(y_i)$$
${\eta }_l$为学习率。接着，客户端的更新$y_i-x$（模型增量）将在服务器端进行聚合：
$$x\leftarrow x+\frac{{\eta }_g}{|S|}\sum _{i\in S}(y_i-x)$$
即对增量进行聚合。当然也可以直接对更新后的模型进行聚合：
$$x\leftarrow \frac{{\eta }_g}{|S|}\sum _{i\in S}{y}_i$$

4. SCAFFOLD

与FedAvg不同的是，SCAFFOLD为每个客户端（客户端控制变量$c_i$）和服务器（服务器控制变量$c$）设置了控制变量，

两种控制变量间的关系：
$$c=\frac{1}{N}\sum c_i$$
即服务器的控制变量为所有客户端控制变量的平均值，所有控制变量都需要进行初始化，最简单的情况是都初始化为0。

SCAFFOLD算法的伪代码：

每一轮通信中，服务器端的参数$(x,c)$（模型+控制变量）都被发送到被选中的客户端$S$。每一个被选中的客户端都将其本地模型初始化为$y_i\leftarrow x$，然后进行本地更新：
$$y_i\leftarrow y_i-{\eta }_l(g_i(y_i)+c-c_i)$$
等到$K$次本地更新完毕后，局部控制变量$c_i$也需要进行更新，作者提供了两种更新选择：

选项I可能比II更稳定，具体取决于应用程序，但II的计算成本更低，而且通常足够（论文中所有的实验都使用选项II）。

局部控制变量更新后，对全局模型进行更新：
$$\begin{gathered} x\leftarrow x+\frac{{\eta }_g}{|S|}\sum _{i\in S}(y_i-x) \\ c\leftarrow c+\frac{1}{N}\sum _{i\in S}(c_i^{+}-c_i) \end{gathered}$$
当然，我们也可以直接对更新后的模型进行聚合：
$$\begin{gathered} x\leftarrow \frac{{\eta }_g}{|S|}\sum _{i\in S}{y}_i \\ c\leftarrow \frac{1}{N}\sum _{i\in S}{c}_i^{+} \end{gathered}$$
我们可以观察本地模型更新公式：
$$y_i\leftarrow y_i-{\eta }_l(g_i(y_i)+c-c_i)$$
如果局部控制变量$c_i$总是为0，那么更新公式将变为：
$$y_i\leftarrow y_i-{\eta }_l{g}_i(y_i)$$
也就是说，SCAFFOLD将退化为FedAvg。

有效性分析

可以发现，SCAFFOLD只是在FedAvg的基础上增加了一个修正项$c-c_i$，就可以有效缓解本地客户端的client-drift，这其中的机理是什么呢？

我们知道，如果通信成本不是问题，最理想的客户端更新机制应该为：
$$y_i\leftarrow y_i+\frac{1}{N}\sum _j{g}_j(y_i)$$
这种更新本质上是计算损失函数$f$的无偏梯度，相当于在IID情况下运行FedAvg，但是这样的更新需要在每个更新步骤中与所有客户端进行通信。

与之对比，SCAFFOLD使用了控制变量（选项I）：

因为SCAFFOLD的本地更新方式为：
$$y_i\leftarrow y_i-{\eta }_l(g_i(y_i)+c-c_i)$$
又有：

所以SCAFFOLD通过控制变量来近似模拟了理想状态下的更新。

因此，对于任意异质的客户端，SCAFFOLD的本地更新保持同步和收敛。

通俗点解释：

我们观察控制变量的更新：

可以发现，控制变量中含有该客户端模型的更新方向（梯度）信息。

全局控制变量$c$是所有客户端本地控制变量的均值，也就是说全局控制变量$c$中含有其他所有客户端的模型更新方向信息。

然后本地更新方式：
$$y_i\leftarrow y_i-{\eta }_l(g_i(y_i)+c-c_i)$$
$c-c_i$我们可以理解为全局模型相对于本地模型的client-drift值，也就是说我们在对本地模型进行更新时考虑了这种差异，这将有效克服client-drift。

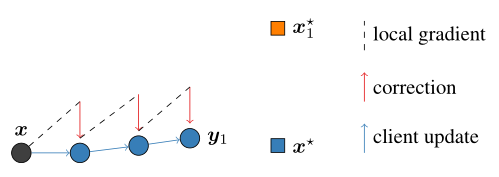
可视化解释如下：

对于单个客户端，接收服务端的模型$x$然后进行更新，如果采用FedAvg的更新机制，那么最优解将向着$x_1^{\ast }$移动，但加入一个修正项$c-c_i$后，将对模型的更新方向产生一个修正，使其朝着真正的最优解$x^{\ast }$移动。

5. 实验

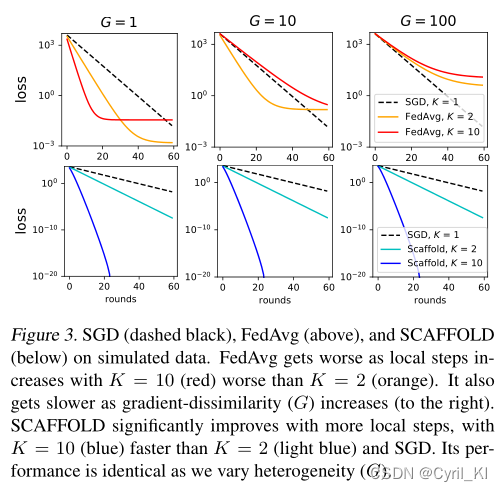
5.1 模拟数据集

将梯度异质性（A1）变为$G\in [1,10,100]$。可以发现，对于所有的G值，随着局部更新次数的增加，FedAvg收敛变慢。这是因为随着本地更新次数的增加，客户端漂移会增加，从而阻碍全局收敛。此外，当我们增加G时（增加异质性），FedAvg的收敛继续减缓。当异质性很小（$G=\beta =1$）时，FedAvg可以与SGD竞争。

观察图3的下面三幅图可以发现，SCAFFOLD始终是收敛最快的，并且其收敛性不受G的影响。

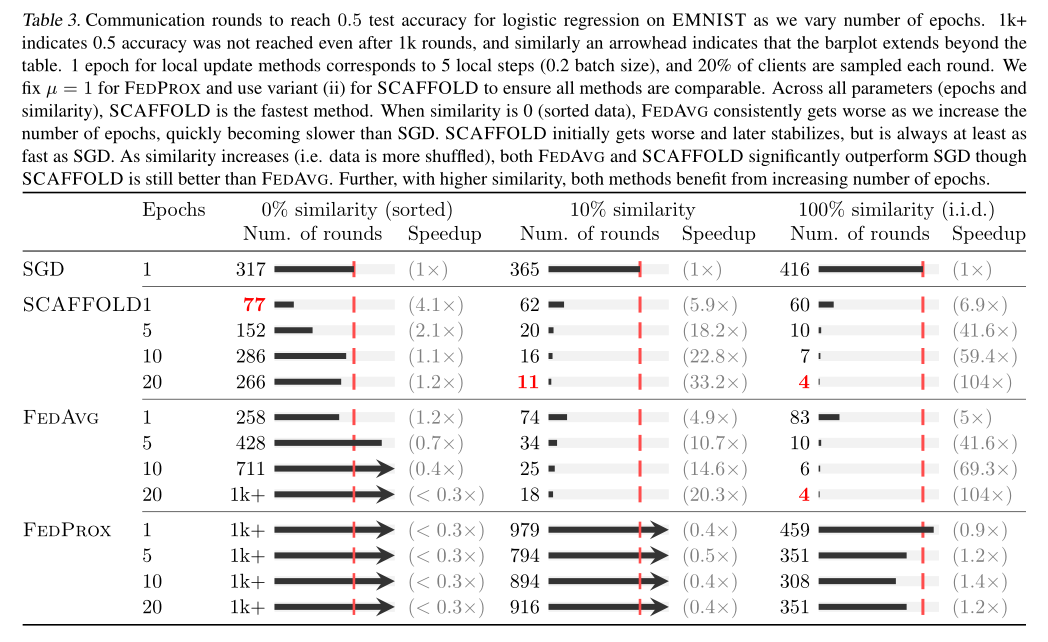
5.2 EMNIST数据集

表3展示了不同本地更新次数（epochs）下，达到逻辑回归的0.5测试精度所需要的通信次数。1K+表示经过1K次通信后仍无法达到0.5精度。

可以发现：

1. SCAFFOLD在所有的相似度中表现都是最好的。
2. 当数据间相似度为0时，FedAvg随着本地更新次数的增加，其通信轮数也在增加，并且最后始终无法达到预定精度。
3. 随着相似度增加，FedAvg和SCAFFOLD都始终优于SGD。
4. FedProx的效果始终是最差的。

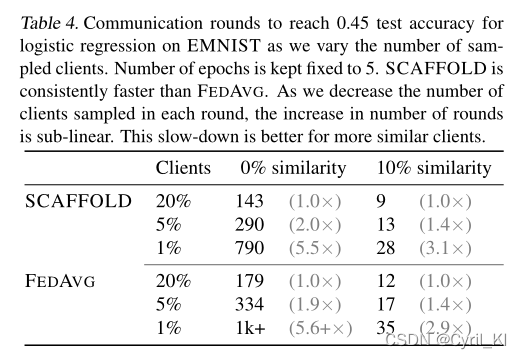
改变抽样客户端的数量，预定精度降为0.45，本地更新次数固定为5，实验结果如下：

可以发现，无论在什么客户端比例下，SCAFFOLD始终优于FedAvg。

5.3 结论

通过上述实验我们可以发现：

1. SCAFFOLD在任何设置下始终优于SGD、FedAvg和FedProx。FedAvg总是比SCAFFOLD慢，比FedProx快。
2. 对于异质客户端来讲，SCAFFOLD > SGD > FedAvg。当本地更新次数大于5时，FedAvg的性能将比SGD差。
3. 随着相似度的增加，SCAFFOLD和FedAvg的收敛都将加快，但SGD保持相对稳定。
4. SCAFFOLD对客户端比例具有弹性。随着减少抽样客户的比例，SCAFFOLD和FedAvg只显示出一种次线性的减速。在相似性较高的情况下，它们对抽样更具弹性。
5. SCAFFOLD在非凸实验中优于FedAvg。

6. 总结

本文研究了异质性对联邦学习优化算法性能的影响。理论分析表明，FedAvg会受到梯度差异的严重阻碍，甚至比SGD还要慢。鉴于此，本文提出了一种新的联邦优化算法SCAFFOLD，SCAFFOLD引入了服务器控制变量$c$和客户端控制变量$c_i$，控制变量中含有模型的更新方向信息，通过在本地模型的更新公式中添加一个修正项$c-c_i$，SCAFFOLD克服了梯度差异，有效缓解了client-drift。