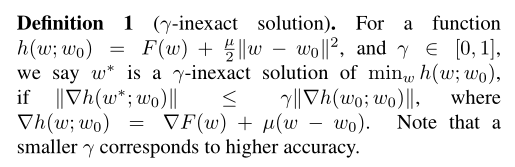I. 前言
FedProx的原理请见:MLSys 2020 | FedProx:异质网络的联邦优化。
II. 数据集介绍
联邦学习中存在多个客户端,每个客户端都有自己的数据集,这个数据集他们是不愿意共享的。
数据集为某城市十个地区的风电功率,我们假设这10个地区的电力部门不愿意共享自己的数据,但是他们又想得到一个由所有数据统一训练得到的全局模型。
III. FedProx
算法伪代码:
1. 模型定义
客户端的模型为一个简单的四层神经网络模型:
# -*- coding:utf-8 -*-
"""
@Time: 2022/03/03 12:23
@Author: KI
@File: model.py
@Motto: Hungry And Humble
"""
from torch import nn
class ANN(nn.Module):
def __init__(self, args, name):
super(ANN, self).__init__()
self.name = name
self.len = 0
self.loss = 0
self.fc1 = nn.Linear(args.input_dim, 20)
self.relu = nn.ReLU()
self.sigmoid = nn.Sigmoid()
self.dropout = nn.Dropout()
self.fc2 = nn.Linear(20, 20)
self.fc3 = nn.Linear(20, 20)
self.fc4 = nn.Linear(20, 1)
def forward(self, data):
x = self.fc1(data)
x = self.sigmoid(x)
x = self.fc2(x)
x = self.sigmoid(x)
x = self.fc3(x)
x = self.sigmoid(x)
x = self.fc4(x)
x = self.sigmoid(x)
return x
2. 服务器端
服务器端和FedAvg一致,即重复进行客户端采样、参数传达、参数聚合三个步骤:
# -*- coding:utf-8 -*-
"""
@Time: 2022/03/03 12:50
@Author: KI
@File: server.py
@Motto: Hungry And Humble
"""
import copy
import random
import numpy as np
import torch
from model import ANN
from client import train, test
class FedProx:
def __init__(self, args):
self.args = args
self.nn = ANN(args=self.args, name='server').to(args.device)
self.nns = []
for i in range(self.args.K):
temp = copy.deepcopy(self.nn)
temp.name = self.args.clients[i]
self.nns.append(temp)
def server(self):
for t in range(self.args.r):
print('round', t + 1, ':')
# sampling
m = np.max([int(self.args.C * self.args.K), 1])
index = random.sample(range(0, self.args.K), m) # st
# dispatch
self.dispatch(index)
# local updating
self.client_update(index, t)
# aggregation
self.aggregation(index)
return self.nn
def aggregation(self, index):
s = 0
for j in index:
# normal
s += self.nns[j].len
params = {}
for k, v in self.nns[0].named_parameters():
params[k] = torch.zeros_like(v.data)
for j in index:
for k, v in self.nns[j].named_parameters():
params[k] += v.data * (self.nns[j].len / s)
for k, v in self.nn.named_parameters():
v.data = params[k].data.clone()
def dispatch(self, index):
for j in index:
for old_params, new_params in zip(self.nns[j].parameters(), self.nn.parameters()):
old_params.data = new_params.data.clone()
def client_update(self, index, global_round): # update nn
for k in index:
self.nns[k] = train(self.args, self.nns[k], self.nn, global_round)
def global_test(self):
model = self.nn
model.eval()
for client in self.args.clients:
model.name = client
test(self.args, model)
3. 客户端更新
FedProx中客户端需要优化的函数为:
h
k
(
w
;
w
t
)
=
F
k
(
w
)
+
μ
2
∣
∣
w
−
w
t
∣
∣
2
h_k(w;w^t)=F_k(w)+\frac{\mu}{2}||w-w^t||^2
hk(w;wt)=Fk(w)+2μ∣∣w−wt∣∣2
作者在FedAvg损失函数的基础上,引入了一个proximal term,我们可以称之为近端项。引入近端项后,客户端在本地训练后得到的模型参数
w
w
w将不会与初始时的服务器参数
w
t
w^t
wt偏离太多。
对应的代码为:
def train(args, model, server, global_round):
model.train()
Dtr, Dte = nn_seq_wind(model.name, args.B)
model.len = len(Dtr)
global_model = copy.deepcopy(server)
if args.weight_decay != 0:
lr = args.lr * pow(args.weight_decay, global_round)
else:
lr = args.lr
if args.optimizer == 'adam':
optimizer = torch.optim.Adam(model.parameters(), lr=lr,
weight_decay=args.weight_decay)
else:
optimizer = torch.optim.SGD(model.parameters(), lr=lr,
momentum=0.9, weight_decay=args.weight_decay)
print('training...')
loss_function = nn.MSELoss().to(args.device)
loss = 0
for epoch in range(args.E):
for (seq, label) in Dtr:
seq = seq.to(args.device)
label = label.to(args.device)
y_pred = model(seq)
optimizer.zero_grad()
# compute proximal_term
proximal_term = 0.0
for w, w_t in zip(model.parameters(), global_model.parameters()):
proximal_term += (w - w_t).norm(2)
loss = loss_function(y_pred, label) + (args.mu / 2) * proximal_term
loss.backward()
optimizer.step()
print('epoch', epoch, ':', loss.item())
return model
我们在原有MSE损失函数的基础上加上了一个近端项:
for w, w_t in zip(model.parameters(), global_model.parameters()):
proximal_term += (w - w_t).norm(2)
然后再反向传播求梯度,然后优化器step更新参数。
原始论文中还提出了一个不精确解的概念:
所谓
γ
\gamma
γ inexact solution:对于一个待优化的目标函数
h
(
w
;
w
0
)
h(w;w_0)
h(w;w0),如果有:
∣
∣
∇
h
(
w
∗
;
w
0
)
∣
∣
≤
γ
∣
∣
∇
h
(
w
0
;
w
0
)
∣
∣
||\nabla h(w^*;w_0)|| \leq \gamma ||\nabla h(w_0;w_0)||
∣∣∇h(w∗;w0)∣∣≤γ∣∣∇h(w0;w0)∣∣
这里
γ
∈
[
0
,
1
]
\gamma \in [0,1]
γ∈[0,1],我们就说
w
∗
w^*
w∗是
h
h
h的一个
γ
−
\gamma-
γ−不精确解。
不过值得注意的是,我并没有在原始论文的实验部分找到如何选择 γ \gamma γ的说明。查了一下资料后发现是涉及到了近端梯度下降的知识,本文代码并没有考虑不精确解,后期可能会补上。
IV. 完整代码及数据
后面将陆续公开~