给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。

示例 1：

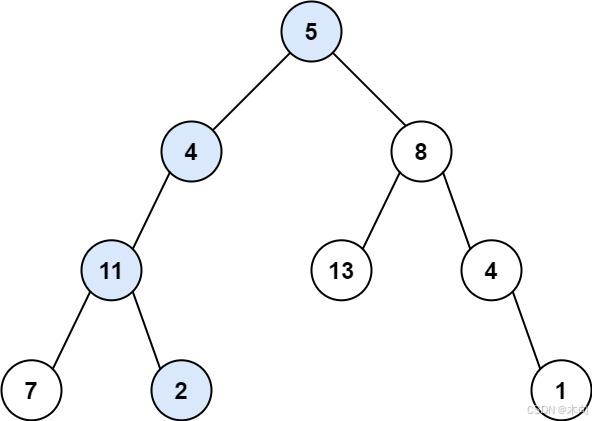
输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

示例 2：

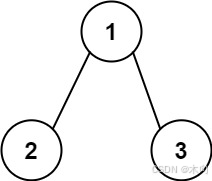
输入：root = [1,2,3], targetSum = 5
输出：false
解释：树中存在两条根节点到叶子节点的路径：
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。

示例 3：

输入：root = [], targetSum = 0
输出：false
解释：由于树是空的，所以不存在根节点到叶子节点的路径。

提示：

• 树中节点的数目在范围 [0, 5000] 内
• -1000 <= Node.val <= 1000
• -1000 <= targetSum <= 1000

步骤1: 问题分析

问题性质：

• 本题是一个经典的二叉树路径和问题，需要判断是否存在一条从根节点到叶子节点的路径，其路径上节点值的和等于给定的 targetSum。

输入条件：

1. 根节点 root：二叉树的根节点。
2. 目标和 targetSum：一个整数，表示目标路径和。

输出条件：

• 返回 true 如果存在符合条件的路径；否则返回 false。

限制与边界条件：

1. 节点范围：节点数目在 [0, 5000] 之间。
2. 节点值范围：[-1000, 1000]。
3. 边界条件：
   • 树为空（root == null），返回 false。
   • 单节点树，检查该节点值是否等于 targetSum。

步骤2: 解题步骤与算法设计

算法设计思路：

• 本题的核心是遍历二叉树并计算路径和，判断是否存在等于 targetSum 的路径。
• 适合的算法：
  1. 深度优先搜索（DFS）：
     • 利用递归，沿着路径累加节点值。
     • 如果到达叶子节点并且路径和等于 targetSum，返回 true。
  2. 广度优先搜索（BFS）：
     • 利用队列同时存储节点和当前路径和，逐层遍历树。
     • 在遍历过程中检查是否存在满足条件的路径。

最佳算法选择：

• DFS 是最佳选择，因为可以直接递归到叶子节点，逻辑简单且代码简洁。
• 时间复杂度：O(N)，其中 N 是节点数，最坏情况下需要访问所有节点。
• 空间复杂度：O(H)，其中 H 是树的高度，递归栈的深度。

具体解题步骤：

1. 边界条件判断：
   • 如果 root == null，直接返回 false。
2. 递归判断路径和：
   • 当前节点的路径和为 当前路径和 + 当前节点值。
   • 如果当前节点是叶子节点且路径和等于 targetSum，返回 true。
   • 否则递归地检查左子树和右子树。
3. 综合左右子树结果：
   • 左右子树只要有一个返回 true，最终结果就为 true。

步骤3: C++ 代码实现

步骤4: 启发与优化

启发：

• 递归可以高效解决树相关问题，但需要注意递归栈的深度限制。
• 考虑边界条件（如空树或单节点树）是避免错误的重要一环。

优化：

• 若树很深，递归可能导致栈溢出，改用迭代方法（BFS）可以避免这一问题。

步骤5: 实际应用场景

行业应用：

场景：电商网站的推荐引擎

• 应用示例：在商品推荐中，构建二叉树表示用户点击路径（每个节点是用户点击的商品），目标是判断是否存在一条点击路径，满足总花费等于用户预算。
• 实现：将用户预算作为 targetSum，树节点值为商品价格，利用上述算法快速判断是否有符合预算的商品组合路径。