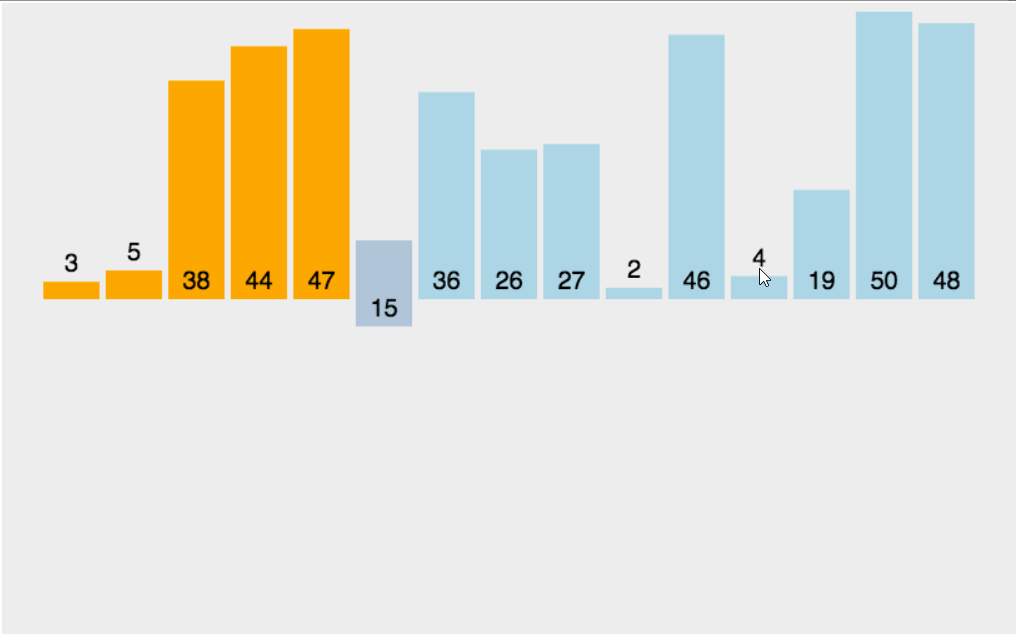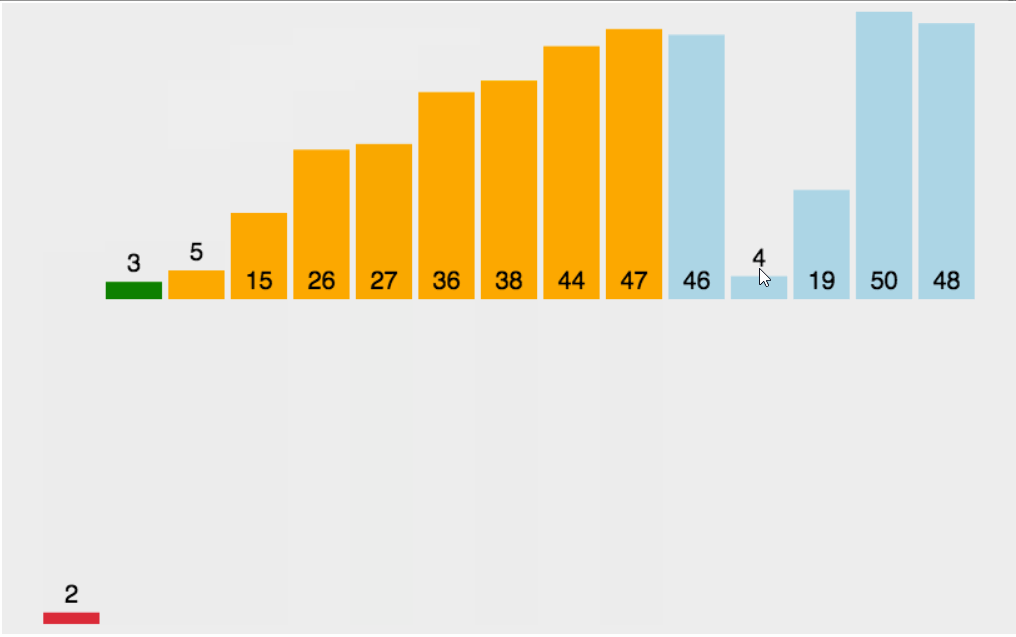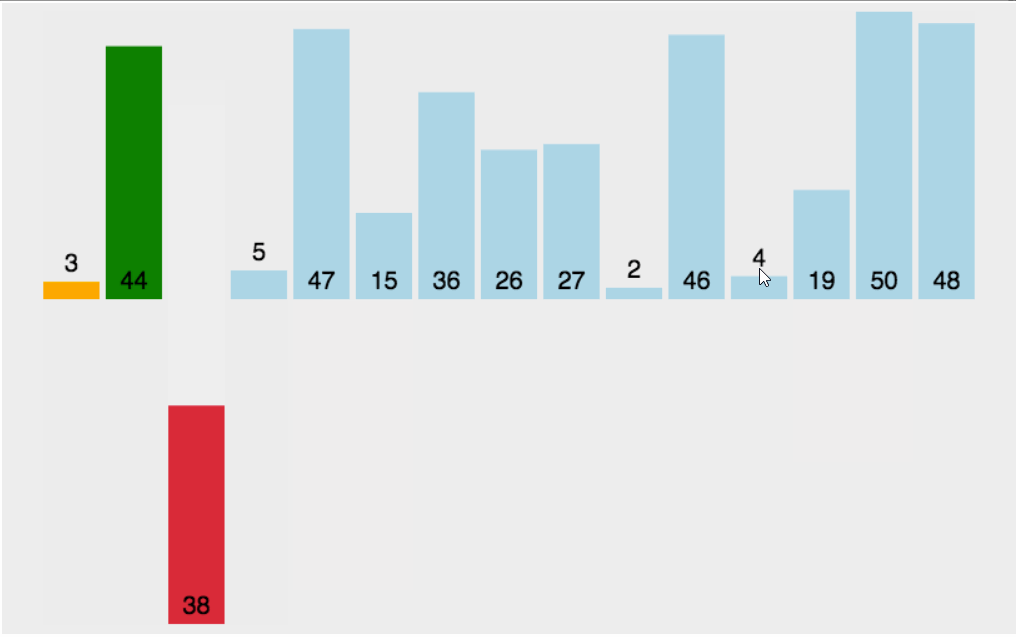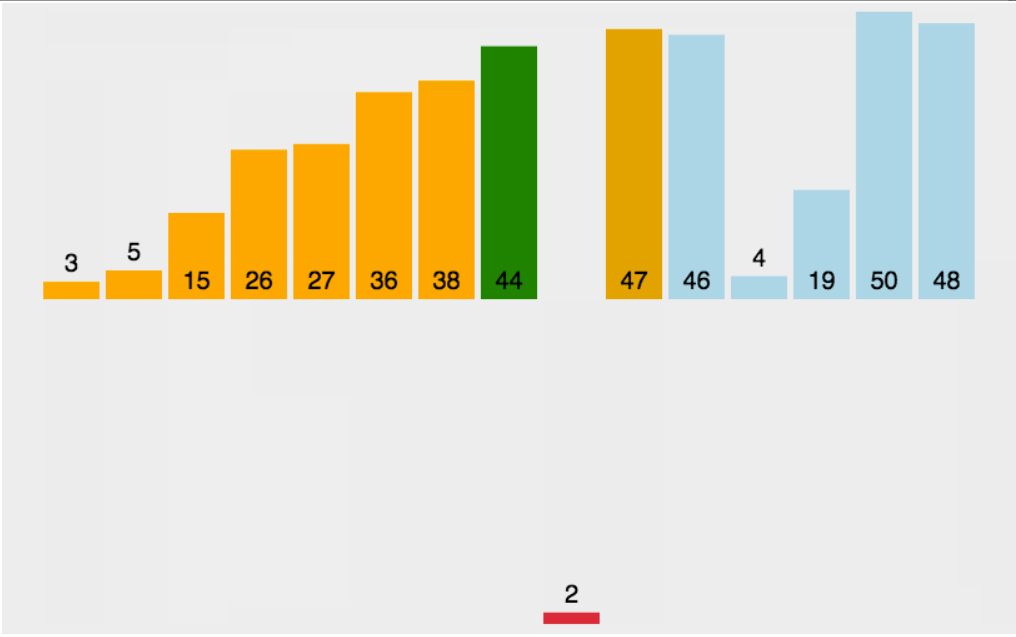目录
1.内部排序
1.1概述
排序(Sorting)是计算机程序设计中的一种重要操作,它的功能是将一个数据元素(或记录)的任意序列,重新排列成一个按关键字有序的序列。
为了查找方便,通常希望计算机中的表是按关键字有序的。因为有序的顺序表可以采用查找效率较高的折半查找法,其平均查找长度为log₂(n+1)-1,而无序的顺序表只能进行顺序查找,其平均查找长度为(n+1)/2。又如建造树表(无论是二叉排序树或 B-树)的过程本身就是一个排序的过程。因此,学习和研究各种排序方法是计算机工作者的重要课题之一。
为了便于讨论,在此首先要对排序下一个确切的定义:
假设含 n个记录的序列为
{R₁,R₂,…, Rn}
其相应的关键字序列为
{K₁,K₂,…, Kn}
需确定1,2,…,n的一种排列p₁,p₂,…, pn,使其相应的关键字满足如下的非递减(或非递增)关系
K₁<=K₂<=…<=Kn
即使第一个序列成为一个按关键字有序的序列
{Rp₁,Rp₂,…, Rpn}
这样一种操作称为排序。
上述排序定义中的关键字 Ki可以是记录 Rᵢ(i=1,2,…,n)的主关键字,也可以是记录 Rᵢ的次关键字,甚至是若干数据项的组合。若Ki是主关键字,则任何一个记录的无序序列经排序后得到的结果是唯一的;若Ki是次关键字,则排序的结果不惟一,因为待排序的记录序列中可能存在两个或两个以上关键字相等的记录。假设Ki=Kj(1≤i≤n,1≤j≤n,i≠j),且在排序前的序列中Ri领先于Rj(即i<j)。若在排序后的序列中Rᵢ仍领先于Rj,则称所用的排序方法是稳定的;反之,若可能使排序后的序列中Rj领先于Ri,则称所用的排序方法是不稳定的。(对不稳定的排序方法,只要举出一组关键字的实例说明它的不稳定性即可。)
由于待排序的记录数量不同,使得排序过程中涉及的存储器不同,可将排序方法分为两大类:一类是内部排序,指的是待排序记录存放在计算机随机存储器中进行的排序过程;另一类是外部排序,指的是待排序记录的数量很大,以致内存一次不能容纳全部记录,因此需要做特殊处理来进行排序...
1.2插入排序
直接插入排序(Straight Insertion Sort)是一种最简单的排序方法,它的基本操作是将一个记录插入到已排好序的有序表中,从而得到一个新的、记录数增1的有序表。
例如,已知待排序的一组记录的初始排列如下所示:①
R(49),R(38),R(65),R(97),R(76),R(13),R(27),R(49),…
假设在排序过程中,前4个记录已按关键字递增的次序重新排列,构成一个含4个记录的有序序列
{R(38),R(49),R(65),R(97)}
现要将第一个式子中第5个(即关键字为76的)记录插入上述序列,以得到一个新的含5个记录的有序序列,则首先要在第二个式子的序列中进行查找以确定R(76)所应插入的位置,然后进行插入。假设从R(97)起向左进行顺序查找,由于65<76<97,则R(76)应插入在R(65)和R(97)之间,从而得到下列新的有序序列
{R(38),R(49),R(65),R(76),R(97)}
称从第二式到第三式的过程为一趟直接插入排序。一般情况下,第i趟直接插入排序的操作为:在含有i-1个记录的有序子序列 r[1.. i-1]中插入一个记录r[i]后,变成含有i个记录的有序子序列r[1..i]。
由于上述过程较为抽象,我们来看看实际应用中插入排序的动图:
步骤及思路:(按照升序排序)
1.将数组分为有序与无序的两个部分
2.将循环设置为0至n-2(这里不能等于n-1的原因是无序的部分不能没有数据)
3.每次循环将有序部分的最后一个下标记录,并将有序部分的下一个,也就是无序部分的第一个保存在tmp变量当中
4.到前面已经有序的部分寻找比tmp小的元素,先跟有序部分的最后一个进行比较,如果tmp大,则直接退出循环,否则从有序部分的最后一个开始,往后移一个单位长度,一直到找到比tmp小的元素,将这个元素后移一个,tmp放入
下面来看代码实现:
void InsertSort(int arr[], int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)
{
int youxu = i;
int tmp = arr[youxu + 1];
while (youxu >= 0)
{
//一直找到小于youxu为止
if (tmp < arr[youxu])
{
arr[youxu + 1] = arr[youxu];
youxu--;
}
else
{
break;
}
}
arr[youxu + 1] = tmp;
}
} 从上面的叙述可见,直接插入排序的算法简洁,容易实现,那么它的效率如何呢?
从空间来看,它只需要一个记录的辅助空间,从时间来看,排序的基本操作为:比较两个关键字的大小和移动记录。先分析一趟插入排序的情况。for 循环的次数取决于待插记录的关键字与前i一1个记录的关键字之间的关系。若L.r[i]key<L.r[1].key,则内循环中,待插记录的关键字需与有序子序列L.r[1..i-1]中i-1个记录的关键字和tmp中的关键字进行比较,并将L.r[1..i-1]中 i-1个记录后移。
则在整个排序过程(进行n一1趟插入排序)中,当待排序列中记录按关键字非递减有序排列(以下称之为“正序”)时,所需进行关键字间比较的次数达最小值n-1,记录不需移动;反之,当待排序列中记录按关键字非递增有序排列(以下称之为“逆序”)时,总的比较次数达最大值(n+2)(n-1)/2,记录移动的次数也达最大值(n+4)(n-1)/2,若待排序记录是随机的,即待排序列中的记录可能出现
的各种排列的概率相同,则我们可取上述最小值和最大值的平均值,作为直接插人排序时所需进行关键字间的比较次数和移动记录的次数,约为n^2/4。由此,直接插入排序的时间复杂度 O(n^2)
1.2.1其他插入排序
从上一节的讨论中可见,直接插入排序算法简便,且容易实现。当待排序记录的数量n很小时,这是一种很好的排序方法。但是,通常待排序序列中的记录数量n很大,则不宜采用直接插入排序。由此需要讨论改进的办法。在直接插入排序的基础上,从减少“比较”和“移动”这两种操作的次数着眼,可得下列各种插入排序的方法。
1.2.1.1 折半插入排序
由于插入排序的基本操作是在一个有序表中进行查找和插入,那么这个查找就可以考虑利用”折半查找”来实现,这里就不多介绍代码原理,仅进行有关讨论,折半插入排序仅减少了关键字间的比较次数,而记录的移动次数不变,因此,折半插入排序的时间复杂度仍然为O(n^2)。
1.2.1.2 2-路插入排序
2-路插入排序是在折半插入排序的基础上再改进之,其目的是减少排序过程中移动记录的次数,但为此需要n个记录的辅助空间。具体做法是:另设一个和L.r同类型的数组d,首先将L.r[1]赋值给d[1],并将 d[1]看成是在排好序的序列中处于中间位置的记录,然后从L.r中第2个记录起依次插入到d[1]之前或之后的有序序列中。先将待插记录的关键字和dL1]的关键字进行比较,若L.r[i].key<d[1].key,则将L.r[i]门插入到d[1]之前的有序表中。反之,则将L.r[i][插入到d[1]之后的有序表中。在实现算法时,可将d看成是一个循环向量,并设两个指针first 和final分别指示排序过程中得到的有序序列中的第一个记录和最后一个记录在d中的位置。
具体代码就不详细撰写,我们来讨论这类插入排序的性能:2-路插入排序中,移动记录的次数约为n^2/8,时间复杂度为O(n^2),且只能减少移动记录的次数,而不能绝对避免移动记录。并且,当L.r[1]是待排序记录中关键字最小或最大的记录时,2-路插入排序就完全失去它的优越性。
1.3希尔排序
希尔排序(Shell’s Sort)又称“缩小增量排序”(Diminishing Increment Sort),它也是种属插入排序类的方法,但在时间效率上较前述几种排序方法有较大的改进。
从对直接插入排序的分析得知,其算法时间复杂度为O(n^2),但是若待排记录序列为“正序”时,其时间复杂度可提高至 O(n)。由此可设想,若待排记录序列按关键字“基本有序”,即序列中具有下列特性
L.r[i].key<max{L.r[j].key} (1<=j<i)
的记录较少时,直接插入排序的效率就可大大提高,从另一方面来看,由于直接插人排序算法简单,则在n值很小时效率也比较高。希尔排序正是从这两点分析出发对直接插入排序进行改进得到的一种插入排序方法。
它的基本思想是:先将整个待排记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
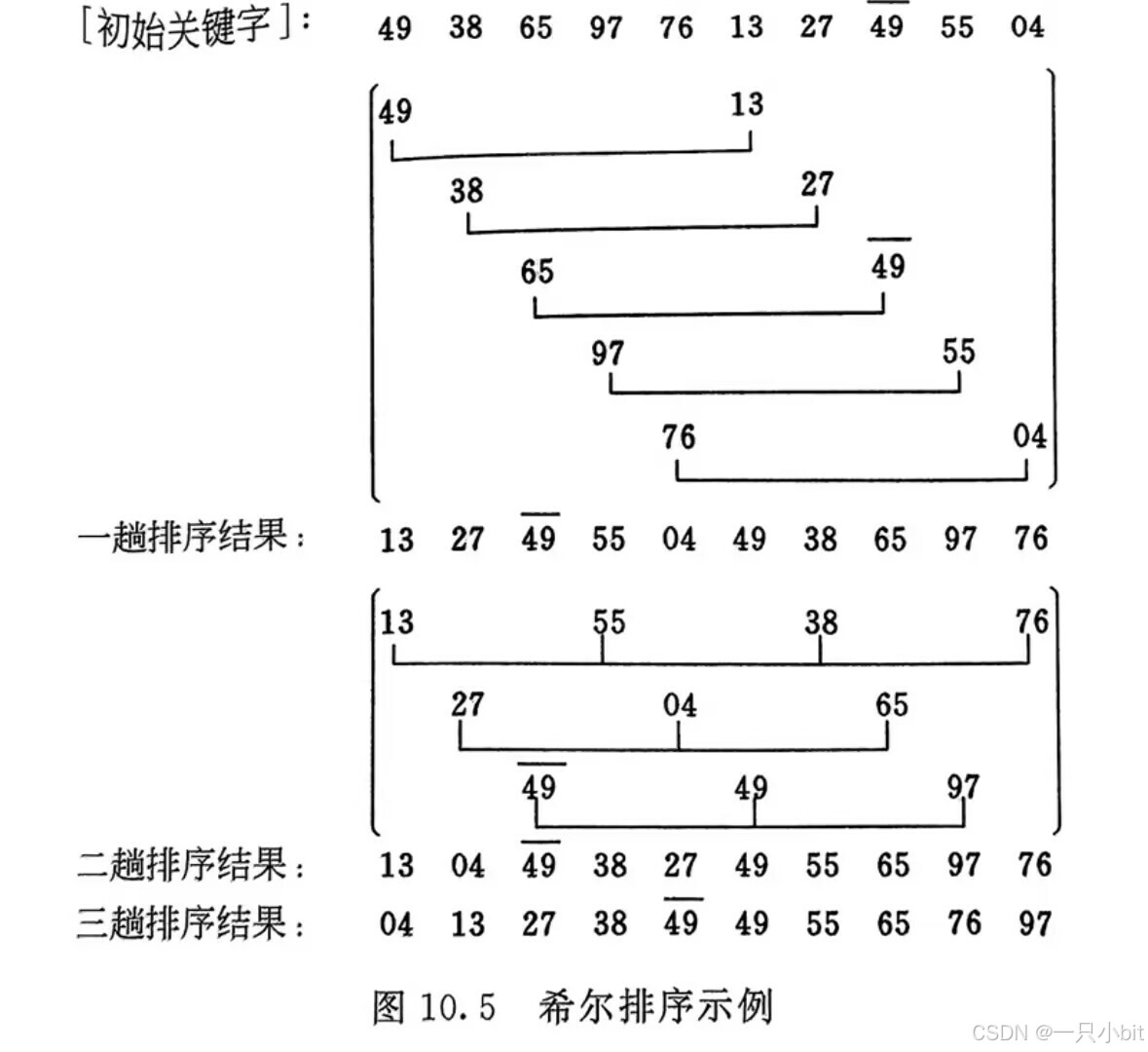
先看一下希尔排序的过程:初始关键字序列如图10.5的第1行所示。首先将该序列分成5个子序列
{R1,R6},{R2,R7},⋯,{R5,R10}
如图10.5的第2行至第6行所示,分别对每个子序列进行直接插入排序,排序结果如图10.5的第7行所示,从第1行的初始序列得到第7行的序列的过程称为一趟希尔排序。然后进行第二趟希尔排序,即分别对下列3个子序列:
{R1,R4,R7,R10},{R2,R5,R8} 和 {R3,R6,R9}
进行直接插入排序,其结果如图 10.5 的第11行所示,最后对整个序列进行一趟直接插入排序。至此,希尔排序结束,整个序列的记录已按关键字非递减有序排列。
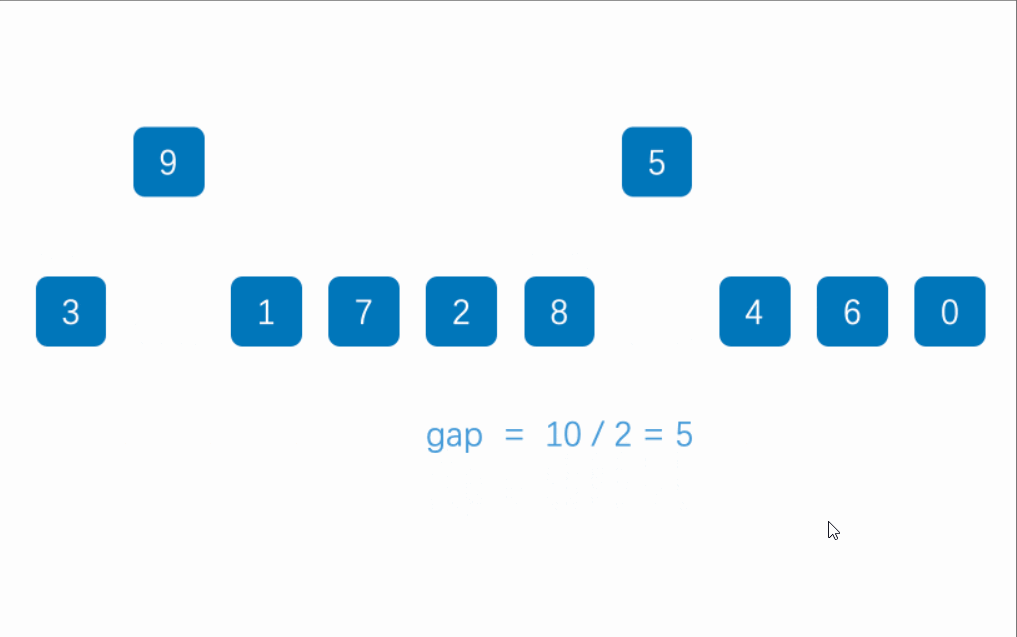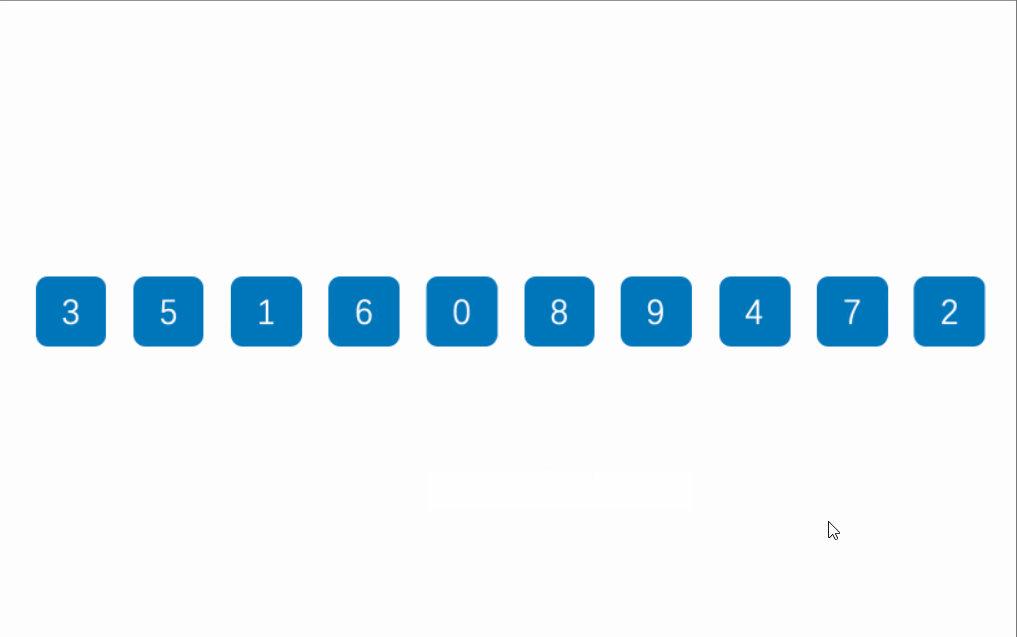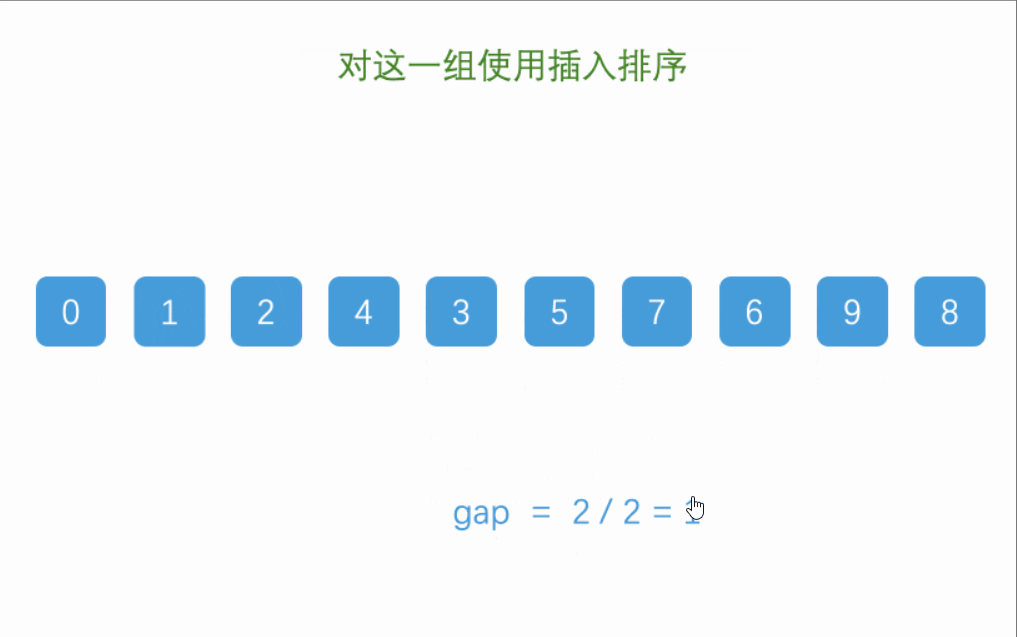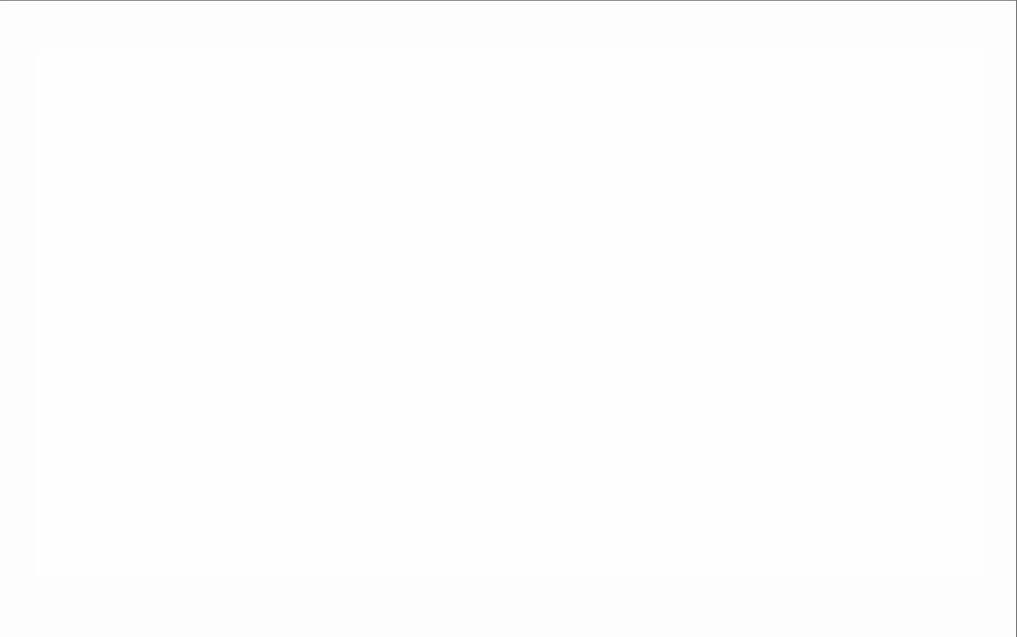
由于上述过程较为抽象,我们来看看实际应用中希尔排序的动图:
步骤及思路:(按照升序排序)
1.先要了解清楚插入排序的基本原理,希尔排序只是对插入排序进行改进,将相邻两个元素进行比较改为相邻gap的元素进行比较
2.首先完成内循环,我们将循环改为0-(n-2*gap),并将每次循环的增量改为gap,其他也是在插入排序的基础之上稍加改动,将有序部分最后一个距离gap的元素保存在tmp中,再进行跨度为gap的寻找较小元素
3.外循环我们对gap进行调整,将gap的初始值设为n,每次循环时/=2,缩小跨度,直到gap为1,循环结束,排序完成,注意:这里必须确保gap最后一定要为1,来完成对基本有序的数组的最后一次排序
下面来看代码实现:
void ShellSort(int* arr, int n)
{
int gap = n;
//gap可以改变,不停变化,本质还是插入
while (gap > 1)
{
gap /= 2;
int j = 0;
for (j = 0; j < gap; j++)
{
int i = 0;
for (i = j; i < n - gap; i += gap)
{
int youxu = i;
int tmp = arr[youxu + gap];
while (youxu >= 0)
{
if (tmp < arr[youxu])
{
arr[youxu + gap] = arr[youxu];
youxu -= gap;
}
else
{
break;
}
}
arr[youxu + gap] = tmp;
}
}
//或者
/*int i = 0;
for (i = j; i < n - gap; i++)
{
int youxu = i;
int tmp = arr[youxu + gap];
while (youxu >= 0)
{
if (tmp < arr[youxu])
{
arr[youxu + gap] = arr[youxu];
youxu -= gap;
}
else
{
break;
}
}
arr[youxu + gap] = tmp;
}*/
}
}我们来看希尔排序的性能:
这是出自数据结构C语言版(严蔚敏)中对希尔排序性能的分析,我们可以进行参考,实际上,希尔排序的时间复杂度呈现的是先上升后下降的趋势,需要复杂的数学分析来证明希尔排序的具体复杂度,我们只需了解平均复杂度即可。
1.4快速排序
1.4.1起泡排序
这一节讨论一类借助“交换”进行排序的方法,其中最简单的一种就是人们所熟知的起泡排序(又称冒泡排序) (Bubble Sort),起泡排洋的过程很简单。首先将第一个记录的关键字和第二个记录的关键学进行比较,若为逆序(即L.r[1].key>L.r[2].key),则将两个记录交换之,然后比较第二个和第三个记录的关键字。以此类推,直至第n-1个记录和第n个记录的关键字进行过比较为止。上述过程叫做第一趟起泡排序,其结果使得关键字最大的记录被安置到最后一个记录的位置上。然后进行第二趟起泡排序,对前n-1个记录进行同样操作,其结果是使关键字次大的记录被安置到第n一1个记录的位置上。一般地,第i趟起泡排序是从L.r[1]到L.r[n-i+1]依次比较相邻两个记录的关键字,并在“逆序”时交换相邻记录,其结果是这n-i+1个记录中关键字最大的记录被交换到第n-i+1的位置上。整个排序过程需进行k(1<=k<n)趟起泡推序,显然,判别起泡排定结束的条件应该是“在一趟排序过程中没有进行过交换记录的操作(这可以作为我们优化冒泡排序的入手点)”图10.6展示了起泡排序的一个实例。从图中可见,在起泡排序的过程中,关键字较小的记录好比水中气泡逐趟向上飘浮,而关键字较大的记录好比石块往下沉,每一趟有一块“最大”的石头沉到水底。
由于上述过程较为抽象,我们来看看实际应用中冒泡排序的动图:
步骤及思路:(按照升序进行排序)
1.设置外层循环,使内层循环每次的循环终点依次减少(这里也可以代表循环起点依次增加),一直到n-2,(这里不设为n-1的原因是还要留下一个元素进行比较和交换)
2.设置内层循环,使数组的第j个元素和第j+1个元素进行比较,直到达到循环终点,也可以设置为从循环起点开始第j个元素与第j+1个元素比较,直到到达数组末尾
3.在内层循环中如果发现第j个元素比第j+1个元素大,就进行交换
4.优化:设置一个布尔类型的变量,如果在内层循环中进行过交换就将变量改为1,否则为0,这样可以判断内层循环所代表的数组的部分是否有序,如果已经有序就跳出外层循环,排序完成
下面来看代码实现:
void BubbleSort(int* arr, int n)
{
int i = 0;
for (i = 0; i < n - 1; i++)
{
int j = 0;
bool judge = false;
for (j = 0; j < n - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
int tmp = arr[j + 1];
arr[j + 1] = arr[j];
arr[j] = tmp;
judge = true;
}
}
if (judge == false)
{
break;
}
}
}分析起泡排序的效率,容易看出,若初始序列为“正序”序列,则只需进行一趟排序,在排序过程中进行n-1次关键字间的比较,且不移动记录;反之,若初始序列“逆序”序列,则需进行n-1躺排序,需进行n(n-1)/2次比较,并作等数量级的记录移动,因此,总的时间复杂度为O(n^2)。
1.4.2快速排序
快速排序(Quick Sort)是对起泡排序的一种改进。它的基本思想是,通过一趟排序将待排记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
假设待排序的序列为
{L.r[s],L.r[s+1],…,L.r[t ])
首先任意选取一个记录(通常可选第一个记录 L.r[s])作力枢轴(或支点)(pivot),然后按下述原则重新排列其余记录:
将所有关键字较它小的记录都安置在它的位置之前,将所有关键字较它大的记录都安置在它的位置之后。由此可以该“枢轴”记录最后所落的位置;作分界线,将序列
{L.r[s],⋯,L.r[t]}
分割成两个子序列
{L.r[s],L.r[s+1] ⋯ L Li-1]}和{L.r[i+1],L.r[i+2],⋯,Lr[t] }
这个过程称做一趟快速排序(或一次划分)。
一趟快速排序的具体做法是:附设两个指针begin和end,它们的初值分别为left和right,设枢轴记录的关键字为key) 则首先从right所指位置起向前搜索找到第一个关键字小于key的记录和枢轴记录互相交换,然后从left所指位置起向后搜索,找到第一个关键字大于 key的记录和枢轴记录互相交换,重复这两步直至left=right为止。
1.4.2.1hoare版本
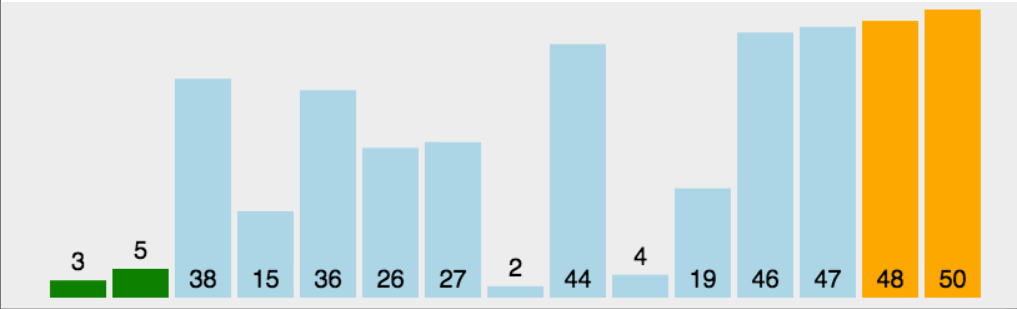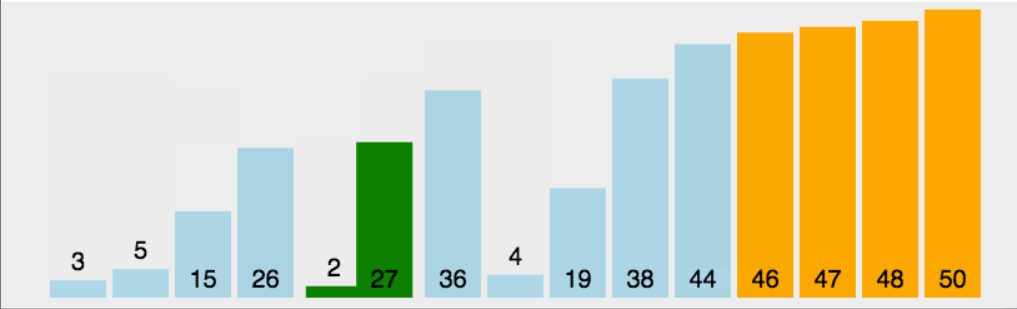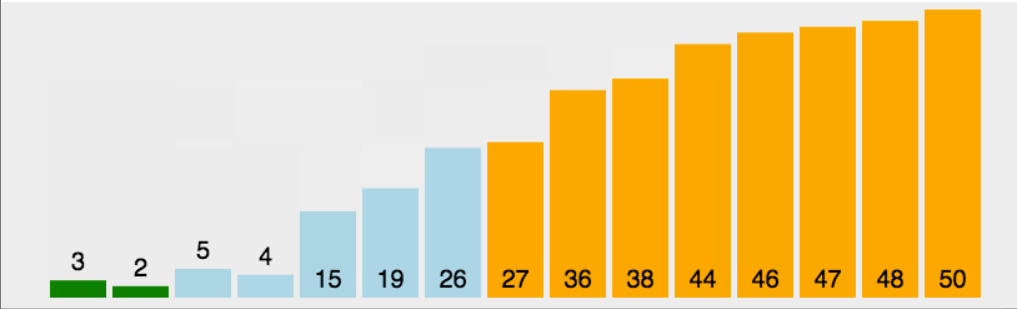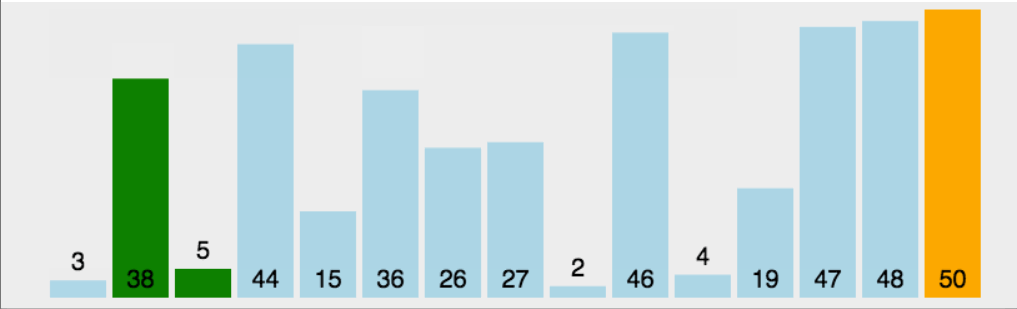
霍尔的快速排序也是最开始快速排序的版本,让我们先看快速排序的动图了解原理:
步骤及原理:(按照升序排序)
1.先将数组首地址,开始元素下标和末尾元素下标传入,将左下标赋给begin变量保存,右下标赋给end变量保存,定义key变量来保存left元素下标
2.在left小于right的前提下,我们从右边开始找比key对应的数组元素还要小的元素,从左边开始找比key对应的数组元素还要大的元素,找到之后我们将这两个元素交换,反复这个过程,设为外层循环,直到left不再小于right,外层循环结束
3.将key对应的元素与此时left和right共同指向的那个元素交换,将key设为left或right,调用递归两次(前面我们保存了begin和end,这里key设定完毕后将数组分为了两段,分别为begin~key-1以及key+1~end),请注意这里key对应的数组元素已经排在了正确的位置上,并且确保数组左边的元素比这个元素小,右边的比这个元素大,为递归调用提供了前提。
下面是代码实现:
//这里其实是两路划分,当数组接近有序时,就会退化成n方
void QuickSort1(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int begin = left;
int end = right;
//随机数取数
/*int randi = left + (rand() % (right - left));
swap(&arr[randi], &arr[left]);*/
//三路取中
int midi = GetMidNumi(arr, left, right);
swap(&arr[midi], &arr[left]);
int key = left;
while (left < right)
{
//左边做key让右边先走,相遇位置比key要小,或者就是key的位置
//右边做key让左边先走,相遇位置比key要大
while (left < right && arr[right] >= arr[key])
{
right--;
}
while (left < right && arr[left] <= arr[key])
{
left++;
}
swap(&arr[right], &arr[left]);
}
swap(&arr[key], &arr[left]);
key = left;
QuickSort1(arr, begin, key - 1);
QuickSort1(arr, key + 1, end);
}优化和说明:细心的读者会发现,代码中多了GetMidNumi这个函数,这其实是在对基础版的快速排序进行优化,
1.选择数组第一个元素下标为key并不是绝对的,我们同样可以选择最后一个元素下标为key,前者先让右指针right寻找比关键字小的元素,再让左指针left寻找比关键字大的元素,当两个指针相遇时指向的元素一定比关键字小(这里是霍尔经过大量数据验证出来的结果,不做证明),如果选择后者,那么就要先让左指针left寻找比关键字大的元素,再让右指针right寻找比关键字小的元素,当两个指针相遇时指向的元素一定比关键字大
2.这里还可以使用其他方法来提高快速排序的性能,可以用到一个rand函数来随机选取数组区间内的一个数,来与第一个元素进行交换,这样关键字的下标并没有改变,改变的是关键字的内容,这样可以提升快排的效率
3.上面的随机取数其实并不推荐,我更为推荐三数取中这种方法,即选择数组区间内首个,中间,末尾这三个元素中第二大的元素,因此我完成了GetMidNumi函数的编写:
int GetMidNumi(int* arr, int left, int right)
{
int mid = (left + right) / 2;
if (arr[mid] > arr[left])
{
if (arr[right] > arr[mid])
{
return mid;
}
else if (arr[right] < arr[left])
{
return left;
}
else
{
return right;
}
}
else
{
if (arr[right] < arr[mid])
{
return mid;
}
else if (arr[left] < arr[right])
{
return left;
}
else
{
return right;
}
}
}补充说明:快速排序的递归类似于二叉树遍历中的前序(先序)遍历,具体的递归过程就不做过多赘述,如果对递归调用还存在疑问的读者,不妨去看看本栏目中二叉树的相关遍历知识,介绍了双重递归调用的过程并附有递归展开图。
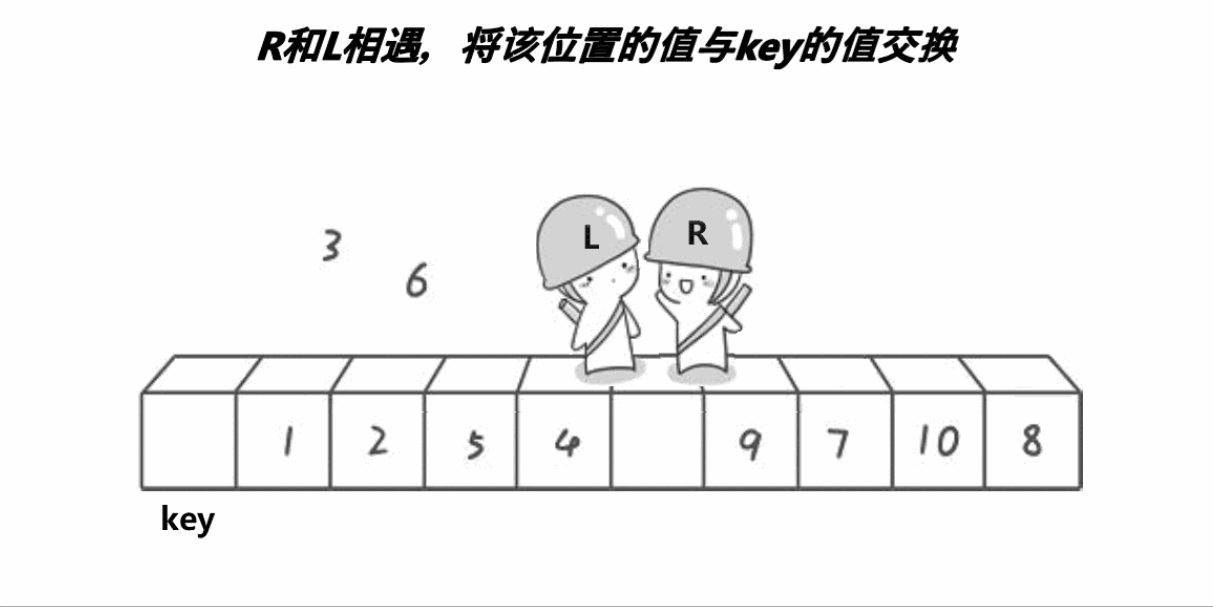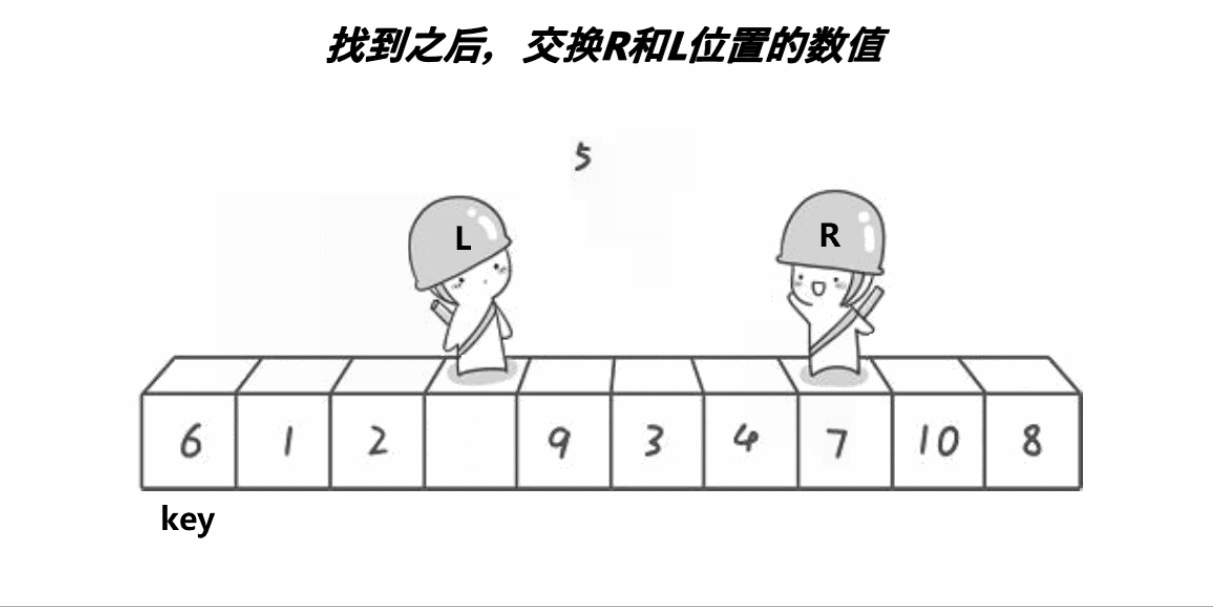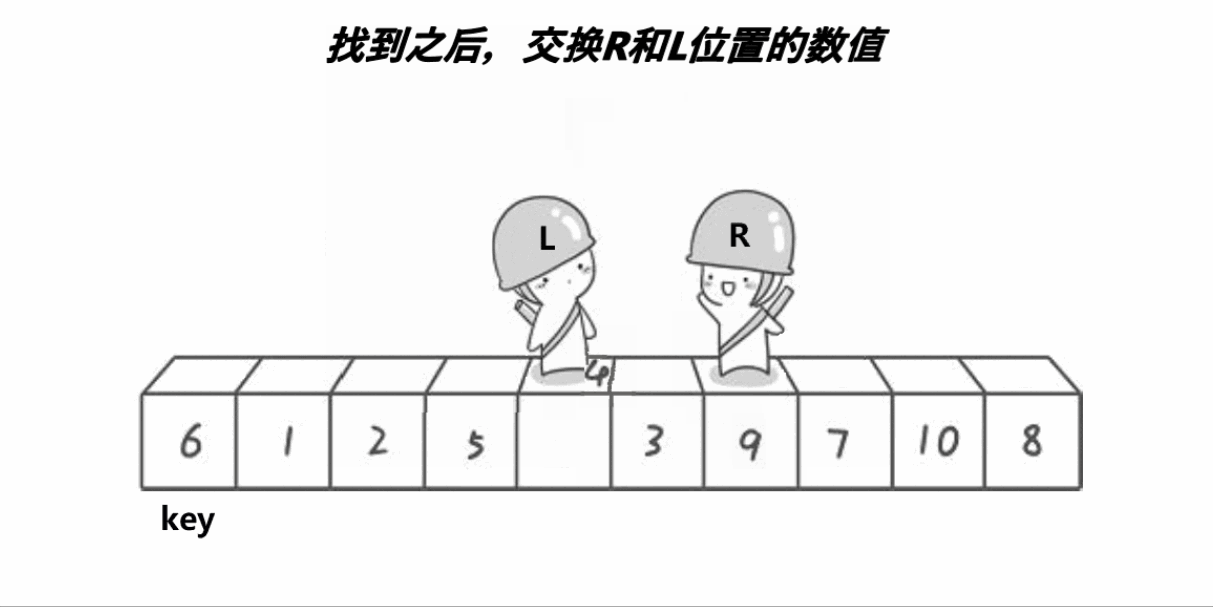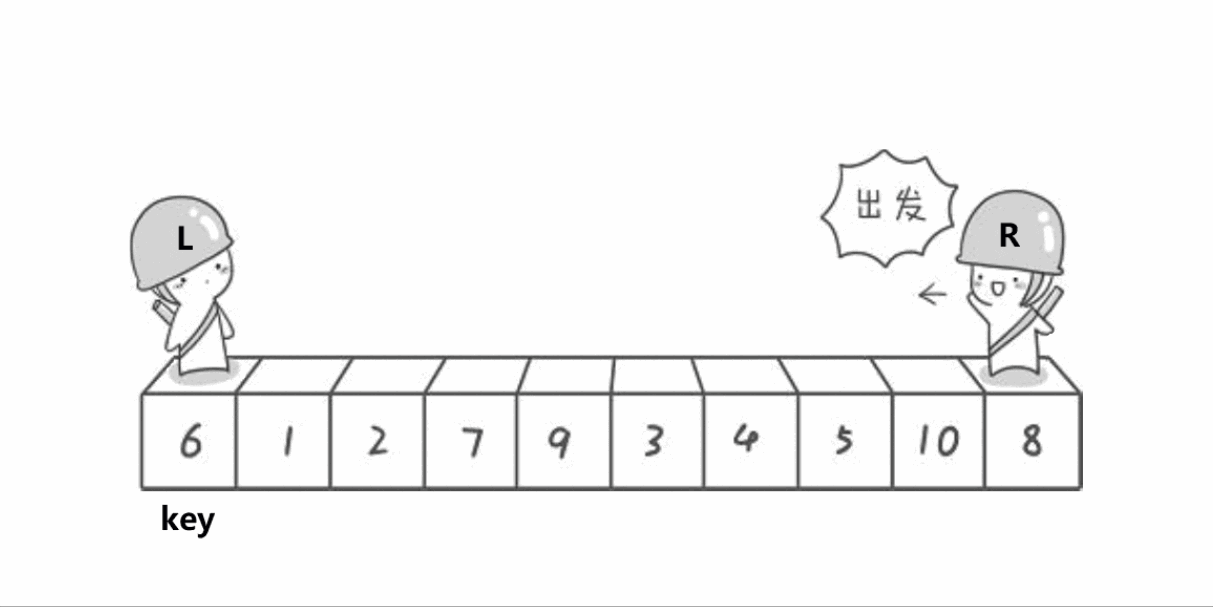
1.4.2.2挖坑版本
这种快速排序实则是对基础班的改进,让我们先通过动图了解原理:
步骤及原理:(按照升序排序)
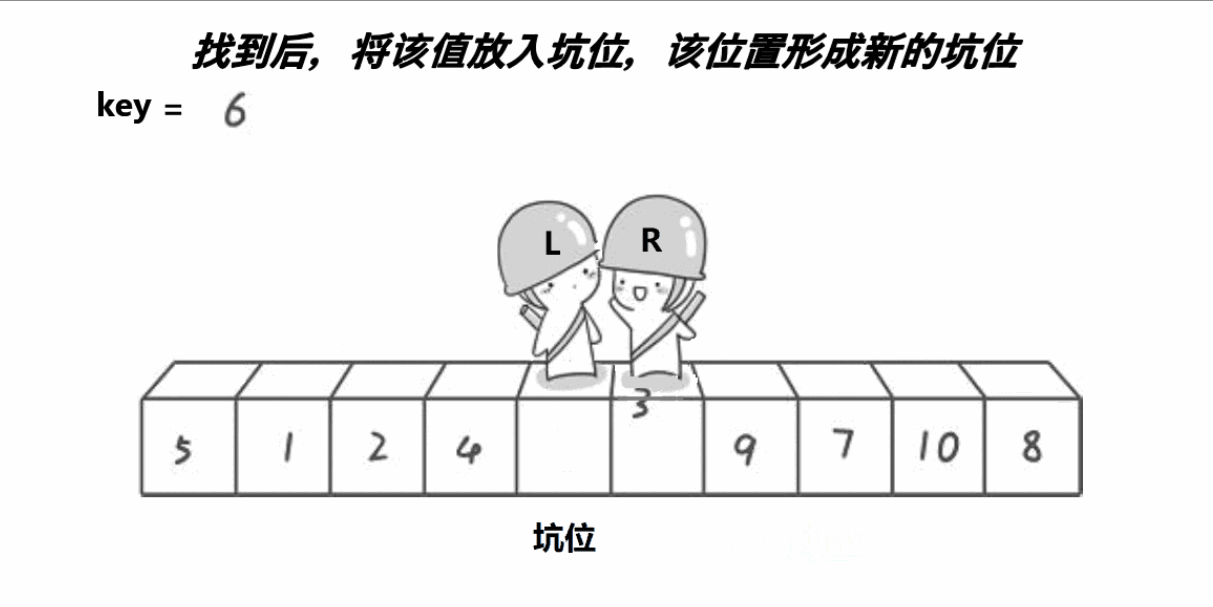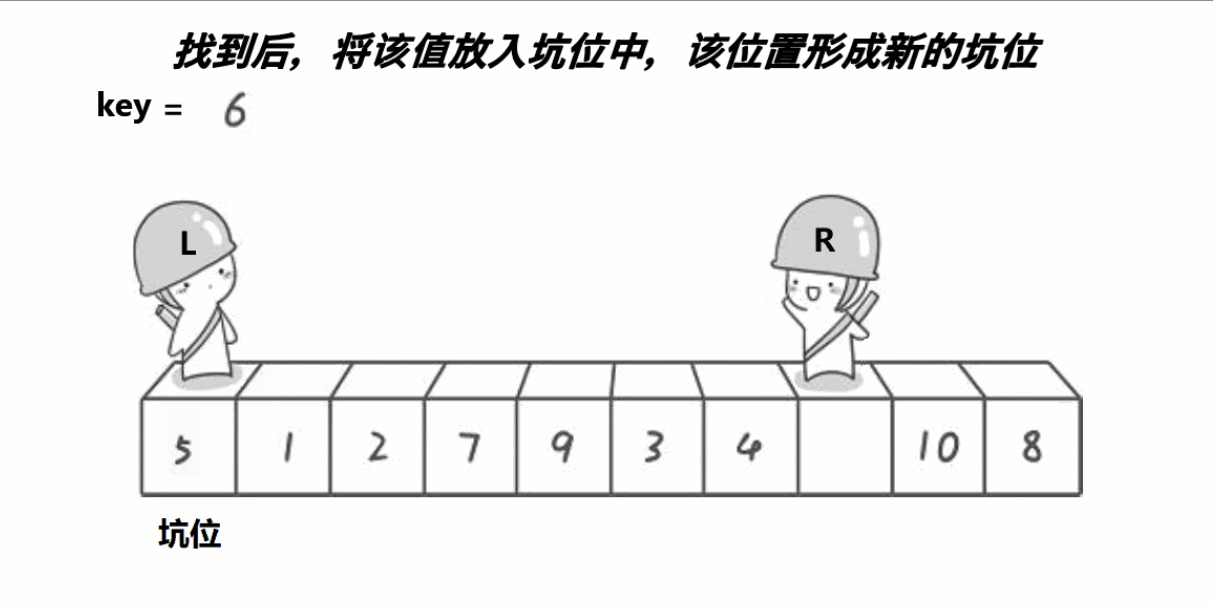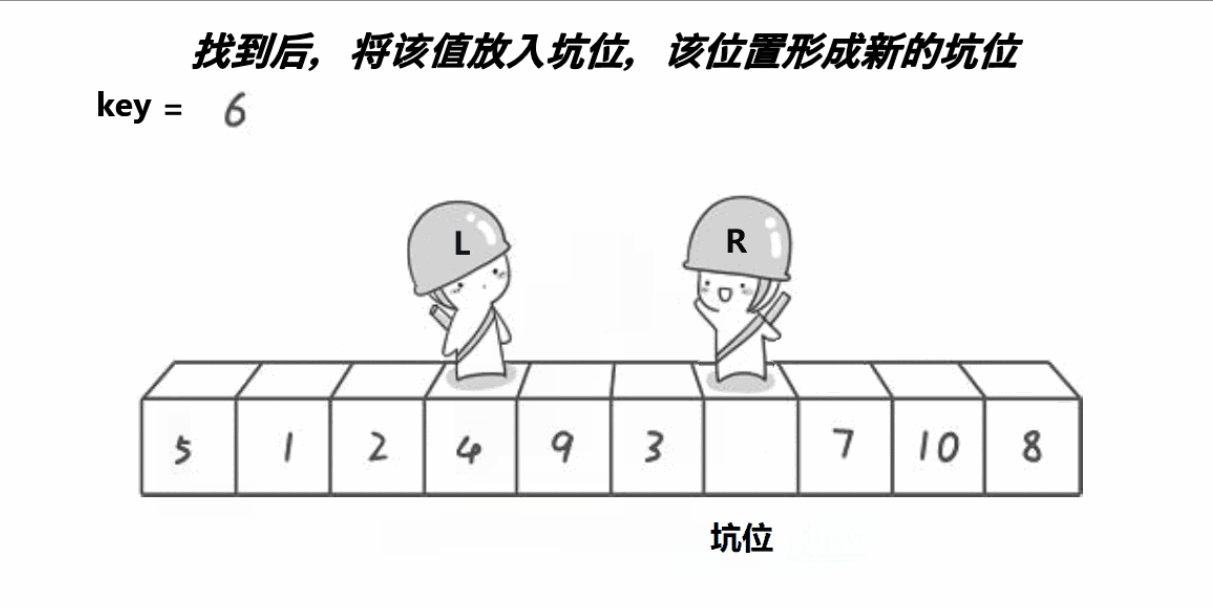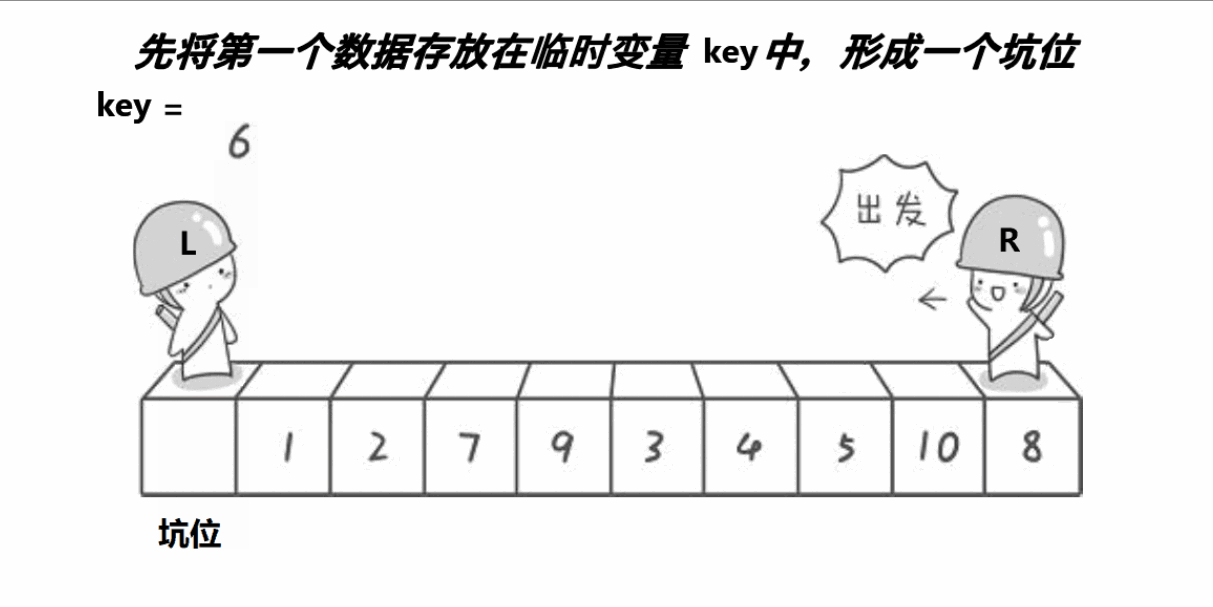
1.先将数组首地址,开始元素下标和末尾元素下标传入,将左下标赋给begin变量保存,右下标赋给end变量保存,定义key变量来保存left元素(注意这里不同于基础版,必须保存元素,如果保存下标会随着坑位改变填入新的元素而改变),定义hole来表示坑位下标
2.在left小于right的前提下,我们从右边开始找比key对应的数组元素还要小的元素,从左边开始找比key对应的数组元素还要大的元素,找到之后我们分别将元素“填入”坑中,将元素赋值给坑,反复这个过程,设为外层循环,直到left不再小于right,外层循环结束
3.将坑内元素赋值为保存的key,将key设为left或right,调用递归两次。
下面是代码实现:
//挖坑法:将key设为坑,找到值后将数丢到坑里
void QuickSort2(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int begin = left;
int end = right;
int hole = left;
int key = arr[left];
while (left < right)
{
//左边做key让右边先走,相遇位置比key要小,或者就是key的位置
//右边做key让左边先走,相遇位置比key要大
while (left < right && arr[right] >= key)
{
right--;
}
arr[hole] = arr[right];
hole = right;
while (left < right && arr[left] <= key)
{
left++;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
key = left;
QuickSort2(arr, begin, key - 1);
QuickSort2(arr, key + 1, end);
}1.4.2.3前后指针版本
前后指针版本是快速排序中最推荐的版本,较为简洁,我们来看一下动图理解原理:
步骤及思路:(按照升序排序)
1.设置两个前后指针,分别是cur和prev,cur保存的是数组第二个元素下标,prev保存的是第一个元素下标,定义key来保存第一个元素的下标,begin和end来保存left和right
2.设置一个外层循环,当cur<=right时循环进行,当cur指向的值比key指向的值要小时,让prev先往后走一个单位,再让cur于prev交换,直到cur>right循环结束
3.将prev对应的元素与key对应的元素交换,将key赋值prev,两次调用递归
下面来看代码实现:
//前后指针版本的快速排序
void QuickSort3(int* arr, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
int prev = left;
int cur = left + 1;
int key = left;
while (cur <= right)
{
if (cur <= right && arr[cur] < arr[key])
{
//找到比key小的就先让prev往前走,再交换,cur最后++
prev++;
swap(&arr[prev], &arr[cur]);
}
cur++;
}
swap(&arr[key], &arr[prev]);
key = prev;
QuickSort3(arr, begin, key - 1);
QuickSort3(arr, key + 1, end);
}
1.4.2.4优化版本
如果想要继续优化快速排序,我们还可以采用以下两种方法:
1.4.2.4.1小区间插入排序优化
在数组区间递归调用时长度小于设定值时,可以采用插入排序的方法直接来对这一个小区间元素进行排序,这样可以起到一定的优化作用,由于插入排序已经在前面做了有关介绍,就不做过多赘述,直接调用:
//对快速排序进行小区间优化
void QuickSort4(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
if (right - left + 1 > 5)
{
int begin = left;
int end = right;
int key = left;
while (left < right)
{
while (left < right && arr[right] >= arr[key])
{
right--;
}
while (left < right && arr[left] <= arr[key])
{
left++;
}
swap(&arr[right], &arr[left]);
}
swap(&arr[key], &arr[left]);
key = left;
QuickSort1(arr, begin, key - 1);
QuickSort1(arr, key + 1, end);
}
else
{
InsertSort(arr + left, right - left + 1);
}
}1.4.2.4.2三路划分优化
由于过程稍微有点复杂,我们配上动图来便于理解:
步骤及思路:(按照升序排序)
1.定义left指向数组第一个元素,定义right指向数组最后一个元素,定义cur指向第二个元素,定义key记录数组第一个元素的数据
2.设置循环,如果cur<=right循环继续,否则循环结束
3.将cur指向的元素与key比较,如果前者小于后者,那么交换left和cur的元素,left向后一个单位,cur向后一个单位,如果两者相等,那么cur向后一个单位,如果前者大于后者,那么交换right和cur的元素,right向前一个单位,cur不动,因为如果right对应元素的值和key需要继续比较
4.和上面大多数快排一样,两次调用递归
下面是代码实现:
//三路划分,大大提高快排的效率
void QuickSort5(int* arr, int left, int right)
{
if (left >= right)
return;
int begin = left;
int end = right;
int key = arr[left];
int cur = left + 1;
while (cur <= right)
{
if (arr[cur] < key)
{
swap(&arr[cur], &arr[left]);
left++;
cur++;
}
else if (arr[cur] == key)
{
cur++;
}
else
{
swap(&arr[right], &arr[cur]);
right--;
}
}
QuickSort5(arr, begin, left - 1);
QuickSort5(arr, left + 1, end);
}1.4.2.5非递归版本
上面所述的都是递归调用的方式实现快速排序,这里我们尝试使用非递归的方式去实现快速排序:
步骤及思路:(按照升序排序)
1.我们定义一个栈结构(具体实现方式本栏也有提到,这里直接调用),先让记录数组最后一个元素下标的right入栈,再让记录数组首个元素下标的left入栈
2.设置循环,当栈不为空时我们取出一个栈顶元素,让这个元素出栈,作为排序数组的begin,再取出一个栈顶元素,出栈后作为排序数组的end
3.调用GetKey函数来获得key的取值,如果key+1<end就让数组的左右下标入栈,如果begin<key-1就让数组的左右下标入栈,直到栈内所有元素都被取出,排序结束
补充:
1.其实在调用GetKey函数获得key的取值时就相当于快速排序的一趟排序
2.这里先入栈右边下标再入栈左边下标遵循了栈的特征,FILO(First In Last Out)先入后出,先让右边入栈,那么取出的第一个就是左边下标,这样方便了我们对排序数组begin和end的定义
下面是代码实现:连通GetKey一并给出!
int GetKey(int* arr, int left, int right)
{
int begin = left;
int end = right;
int key = left;
while (left < right)
{
if (left < right && arr[right] >= arr[key])
{
right--;
}
if (left < right && arr[left] <= arr[key])
{
left++;
}
swap(&arr[right], &arr[left]);
}
swap(&arr[key], &arr[left]);
key = left;
return key;
}
void QuickSortNonR(int* arr, int left, int right)
{
Stack st;
StackInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
int key = GetKey(arr, begin, end);
//在获得key的时候其实就在排序
if (key + 1 < end)
{
StackPush(&st, end);
StackPush(&st, key + 1);
}
if (begin < key - 1)
{
StackPush(&st, key - 1);
StackPush(&st, begin);
}
}
StackDestroy(&st);
}来看看书上关于快速排序性能的讲解:
书中提到,这里优化的方法有三数取中,我们在上面也已经实现,同时,时间复杂度的数量级为O(nlogn),从时间上看,快速排序的平均性能优于前面讨论过的各种排序方式,从空间上看,前面讨论的各种方法,除2-路插入排序,都只需要一个记录的附加空间即可,但快速排序需要一个栈空间来实现递归,即使不使用递归,也需要额外使用栈结构,若每一趟排序都将记录序列均匀地分成长度相接近的两个子序列,则栈的最大深度为[logn]+1,这其实是快速排序的空间复杂度,为O(logn)。
欲知其他排序,请看下文...