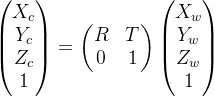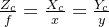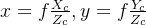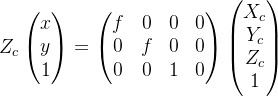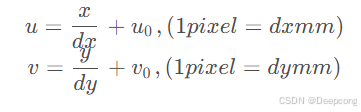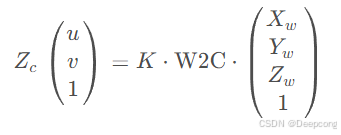坐标系及其转换在计算机视觉领域占据核心地位。理解如何从一个坐标系转换到另一个坐标系，不仅是理论上的需要，也是实际应用中不可或缺的技能。

一、世界坐标系的定义

世界坐标系是一个全局的坐标系统，用于定义场景中物体的位置。在这个坐标系中，每个物体的位置都是相对于一个全局原点来描述的，单位是m，任意一点的坐标表示为，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置，世界坐标系的位置可以根据实际情况自由确定。

二、相机坐标系的定义

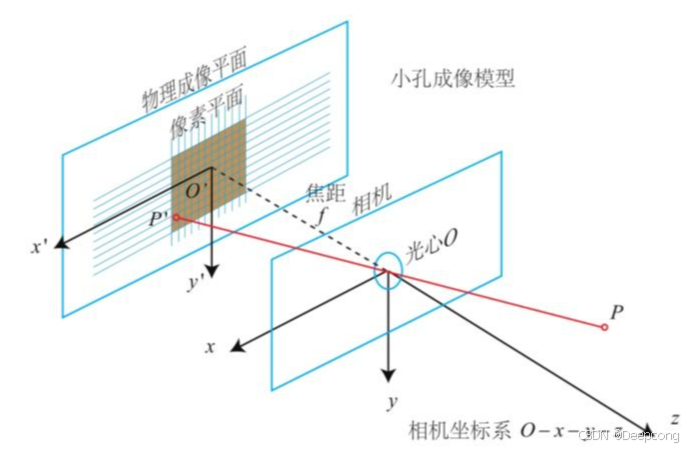
相机坐标系是相对于相机的位置来定义物体的坐标系统。在这个坐标系中，原点通常位于相机的光心，即相机镜头的中心。Z轴通常与相机的观察方向一致，与成像平面垂直，X和Y轴定义相机平面，就是以光圈O为原点的右手坐标系，与世界坐标系位于同一空间，只是位置和方向不同，单位是m，任意一点的坐标表示为。

三、图像物理坐标系的定义

如二中图所示，物理成像平面上的坐标系就是图像物理坐标系，是一个二维坐标系，原点在成像平面的中心，单位是mm，相当于用物理单位描述像素的位置，其中任意一点的坐标可表示为。

四、像素平面坐标系的定义

像素坐标系是图像上的二维坐标系统，用于定义图像上每个像素的位置。原点通常位于图像的左上角，X轴从左到右延伸，Y轴从上到下延伸，单位是像素，从图像物理坐标系到像素平面坐标系存在一个缩放和平移，其中任意一点的坐标表示为。

五、世界坐标系到像素平面坐标系的转换

5.1 先从世界坐标系转换到相机坐标系

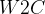
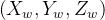
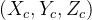
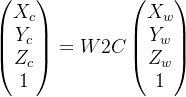
二者处于同一空间，所以只需要平移和旋转，通过外参矩阵完成，假设世界坐标系中的点为，相机坐标系中的点为，转换过程如下：

其中：

是3*3的旋转矩阵，描述相机的旋转；

是3*1的平移向量，描述相机在世界坐标系中的位置；

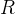
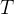
从世界坐标系转换到相机坐标系最终的转换公式如下（涉及到齐次坐标，有空更新）：

这一步完成后，就得到点在相机坐标系中的坐标。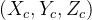

5.2 从相机坐标系到图像物理坐标系

相似那部分重点查看，这篇文章。

根据相似三角形得到的关系式如下：

齐次坐标表示：

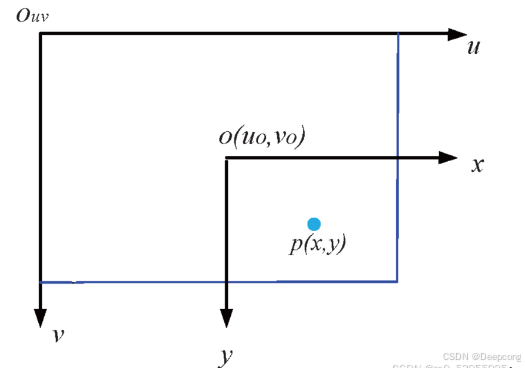
5.3 从图像物理坐标系到像素坐标系

像素坐标系和图像坐标系都在成像平面上，只是各自的原点和度量单位不一样。

图像坐标系的原点为相机光轴与成像平面的交点，通常情况下是成像平面的中点；

像素坐标系的原点在成像平面的左上角；
图像坐标系的单位是mm，是物理单位，而像素坐标系的单位是pixel，我们平常描述一个像素点都是几行几列。所以这两者之间的转换关系如下：

齐次坐标表示：

将以上步骤结合在一起，可以得到从世界坐标系到图像坐标系的完整转换公式：

综上所述，存在的疑惑就是：

1、世界坐标系怎么确定？

分不分静态的相机和运动的相机？

2、相机内参，外参怎么样计算？

‌相机内参的获取通常通过相机标定过程来实现。‌‌

相机内参的定义和作用

相机内参是与相机自身特性相关的参数，主要包括参数矩阵（如fx, fy, cx, cy）以及畸变参数（如k1, k2, k3, p1, p2）。这些参数在相机出厂时通常已被标定，并存储在设备的Flash中。，帮助将三维世界坐标转换到二维图像坐标。

获取相机内参的方法

1. ‌通过相机标定获取内参‌：最常见的获取相机内参的方法是通过相机标定。标定过程通常使用棋盘格等标定图案，通过图像处理和数学计算来估算内参。具体步骤包括拍摄多张标定图案的图片，使用标定算法（如张正友标定法）计算内参。

2. ‌使用现成的标定工具或软件‌：许多相机厂商提供了标定工具或软件，用户可以通过这些工具进行标定以获取相机的内参。例如，OpenCV提供了丰富的相机标定函数，用户可以通过编写代码实现标定过程。

3. ‌通过API获取‌：一些相机设备在出厂时已经标定好内外参，并存储在设备的Flash中。用户可以通过调用设备的API获取这些参数，而无需重新标定。

参考：

https://zhuanlan.zhihu.com/p/128155013

https://blog.csdn.net/m0_51661400/article/details/141395396

世界坐标系到像素坐标系的转换_世界坐标系转相机坐标系-CSDN博客

https://zhuanlan.zhihu.com/p/356546894

https://blog.csdn.net/mzpmzk/article/details/64924017

https://zhuanlan.zhihu.com/p/681072094