前言
【ML-SVM案例学习】会有十种SVM案例,供大家用来学习。本章实现SVM鸢尾花数据的分类任务。
一、完整源码分步实现
1.引入库
代码如下(示例):
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import warnings
from sklearn import svm # svm导入
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.exceptions import ChangedBehaviorWarning
2.读入数据
代码如下(示例):
## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
warnings.filterwarnings('ignore', category=ChangedBehaviorWarning)
## 读取数据
# 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
path = './datas/iris.data' # 数据文件路径
data = pd.read_csv(path, header=None)
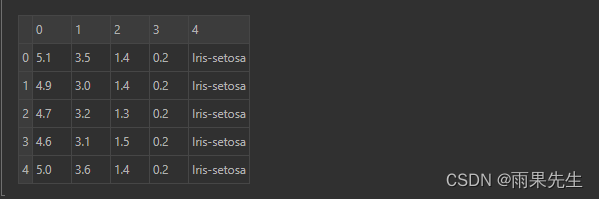
data.head(5)
数据如下:
3.编码数据
x, y = data[list(range(4))], data[4]
y = pd.Categorical(y).codes # 把文本数据进行编码,比如a b c编码为 0 1 2; 可以通过pd.Categorical(y).categories获取index对应的原始值
x = x[[0, 1]] # 获取第一列和第二列
print('经过编码后的数据y:', y[:5])
经过编码后的数据y: [0 0 0 0 0]
4.数据分割
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=0, train_size=0.8)
# svm.SVC API说明:
# 功能:使用SVM分类器进行模型构建
# 参数说明:
# C: 误差项的惩罚系数,默认为1.0;一般为大于0的一个数字,
# C越大表示在训练过程中对于总误差的关注度越高,也就是说当C越大的时候,
# 对于训练集的表现会越好,但是有可能引发过度拟合的问题(overfiting)
# kernel:
# 指定SVM内部函数的类型,可选值:linear、poly、rbf、sigmoid、precomputed(基本不用,有前提要求,要求特征属性数目和样本数目一样);默认是rbf;
# degree:
# 当使用多项式函数作为svm内部的函数的时候,给定多项式的项数,默认为3
# gamma:
# 当SVM内部使用poly、rbf、sigmoid的时候,核函数的系数值,当默认值为auto的时候,实际系数为1/n_features
# coef0:
# 当核函数为poly或者sigmoid的时候,给定的独立系数,默认为0
# probability:
# 是否启用概率估计,默认不启动,不太建议启动
# shrinking:
# 是否开启收缩启发式计算,默认为True
# tol:
# 模型构建收敛参数,当模型的的误差变化率小于该值的时候,结束模型构建过程,默认值:1e-3
# cache_size:
# 在模型构建过程中,缓存数据的最大内存大小,默认为空,单位MB
# class_weight:
# 给定各个类别的权重,默认为空
# max_iter:
# 最大迭代次数,默认-1表示不限制
# decision_function_shape:
# 决策函数,可选值:ovo和ovr,默认为None;推荐使用ovr;(1.7以上版本才有)
5.数据SVM分类器构建
clf = svm.SVC(C=1, kernel='rbf',gamma=0.1)
# gamma值越大,训练集的拟合就越好,但是会造成过拟合,导致测试集拟合变差
# gamma值越小,模型的泛化能力越好,训练集和测试集的拟合相近,但是会导致训练集出现欠拟合问题,
# 从而,准确率变低,导致测试集准确率也变低。
## 模型训练
clf.fit(x_train, y_train)
输出:
SVC(C=1, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=‘ovr’, degree=3, gamma=0.1, kernel=‘rbf’,
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
6.计算模型的准确率/精度
print ('训练集的score:', clf.score(x_train, y_train))
print ('训练集准确率:', accuracy_score(y_train, clf.predict(x_train)))
print ('测试集的score:', clf.score(x_test, y_test))
print ('测试集准确率:', accuracy_score(y_test, clf.predict(x_test)))
输出:
训练集的score: 0.85
训练集准确率: 0.85
测试集的score: 0.7333333333333333
测试集准确率: 0.7333333333333333
7.计算决策函数的结构值以及预测值
# (decision_function计算的是样本x到各个分割平面的距离<也就是决策函数的值>)
print ('decision_function:\n', clf.decision_function(x_train))
print ('predict:\n', clf.predict(x_train))
decision_function:
decision_function:
[[-0.25039727 1.0886331 2.16176417]
[ 1.03478736 2.11650098 -0.15128834]
[ 2.23214438 1.00598335 -0.23812773]
[-0.19163546 2.1175139 1.07412155]
[-0.32152579 1.14496276 2.17656303]
[ 1.02173467 2.16988825 -0.19162293]
[ 2.14580325 0.95677746 -0.10258071]
[-0.23566638 2.17796366 1.05770273]
[-0.13008471 2.12075927 1.00932543]
[-0.19844194 2.1995431 0.99889884]
[-0.36343522 1.08701831 2.27641692]
[ 2.30535715 1.04393285 -0.34929 ]
[-0.35915878 1.06384614 2.29531264]
[ 2.29333629 0.99860275 -0.29193904]
[ 2.21795456 0.97111601 -0.18907056]
[ 0.92054508 2.2724345 -0.19297958]
[-0.2997012 1.10328323 2.19641797]
[-0.2730624 1.03890272 2.23415968]
[-0.33839217 2.26132199 1.07707018]
[-0.44273262 1.17653689 2.26619573]
[-0.15877661 2.21746358 0.94131303]
[-0.44724083 1.02472152 2.42251931]
[-0.17202518 1.05287918 2.119146 ]
[-0.14988387 2.23343312 0.91645074]
[-0.31861821 1.16774019 2.15087802]
[-0.29622421 1.14950193 2.14672228]
[ 1.0664275 2.1904298 -0.2568573 ]
[-0.35991183 1.20227659 2.15763525]
[-0.35330602 1.04124945 2.31205657]
[-0.2997012 1.10328323 2.19641797]
[-0.05522314 2.03779287 1.01743027]
[ 2.25203496 1.06973396 -0.32176891]
[-0.17449621 2.18085941 0.9936368 ]
[-0.11021164 2.18046075 0.92975089]
[-0.05865155 2.14084287 0.91780868]
[-0.12662311 2.21612151 0.9105016 ]
[-0.19163546 2.1175139 1.07412155]
[-0.38070881 1.0296007 2.35110811]
[ 2.24957743 0.96861839 -0.21819582]
[ 2.35477694 1.05478502 -0.40956196]
[-0.34332437 1.16288782 2.18043655]
[-0.06527735 2.12119172 0.94408563]
[ 2.14185505 1.03254567 -0.17440072]
[ 2.27389225 0.85571723 -0.12960948]
[-0.35915878 1.06384614 2.29531264]
[ 2.30724951 1.05732668 -0.3645762 ]
[-0.13008471 2.12075927 1.00932543]
[ 1.00329378 2.20214884 -0.20544262]
[ 2.37889994 0.99914274 -0.37804268]
[-0.38865303 2.25320429 1.13544874]
[-0.29145938 0.96854255 2.32291684]
[-0.09164014 2.14161983 0.95002031]
[ 2.22623117 1.08968182 -0.31591299]
[-0.4096892 1.06746523 2.34222397]
[-0.33660296 1.0467762 2.28982676]
[-0.2997012 1.10328323 2.19641797]
[-0.32152579 1.14496276 2.17656303]
[ 2.33278328 0.94341849 -0.27620177]
[ 2.32663406 1.00960575 -0.33623981]
[-0.25094655 1.06568299 2.18526357]
[-0.2730624 1.03890272 2.23415968]
[ 2.13304331 1.19108118 -0.32412449]
[-0.11663626 1.03526731 2.08136896]
[ 2.19635991 1.09554303 -0.29190293]
[-0.19042462 2.21791314 0.97251148]
[-0.35915878 1.06384614 2.29531264]
[ 2.37987847 1.02502782 -0.40490629]
[ 2.31697854 0.97865204 -0.29563057]
[-0.42101983 1.06048387 2.36053596]
[ 2.26321395 1.00248244 -0.26569639]
[ 2.3322641 1.06231608 -0.39458018]
[ 2.2645061 0.93262533 -0.19713143]
[-0.17206568 2.24979256 0.92227312]
[-0.31794906 1.05203355 2.2659155 ]
[-0.44593685 1.03180134 2.41413551]
[ 2.26321395 1.00248244 -0.26569639]
[ 2.22247594 1.07534695 -0.29782289]
[ 2.20680036 1.02662003 -0.23342039]
[-0.11748127 2.16161947 0.9558618 ]
[-0.32277435 1.09831759 2.22445676]
[ 2.21795026 1.05994599 -0.27789625]
[ 2.21270515 1.04364305 -0.2563482 ]
[-0.2986835 1.12654041 2.17214309]
[ 2.14185505 1.03254567 -0.17440072]
[-0.5 1.07338601 2.42661399]
[ 1.0415998 2.20742886 -0.24902865]
[-0.30569708 0.92274296 2.38295412]
[-0.32111039 1.07499685 2.24611354]
[ 2.36439692 0.89257767 -0.25697458]
[-0.1613555 2.11948124 1.04187426]
[ 2.161655 0.92086513 -0.08252013]
[-0.47608835 1.04954709 2.42654126]
[ 2.33278328 0.94341849 -0.27620177]
[ 2.30535715 1.04393285 -0.34929 ]
[-0.47075253 1.07424442 2.39650811]
[ 2.24367895 1.03936622 -0.28304517]
[-0.14575094 1.03325696 2.11249398]
[-0.11748127 2.16161947 0.9558618 ]
[-0.17449621 2.18085941 0.9936368 ]
[-0.16701198 2.19987473 0.96713725]
[-0.22523374 1.06936924 2.1558645 ]
[-0.34404723 1.09287868 2.25116855]
[-0.35991183 1.20227659 2.15763525]
[-0.34404723 1.09287868 2.25116855]
[ 2.16544172 1.10090524 -0.26634696]
[-0.14988387 2.23343312 0.91645074]
[-0.32111039 1.07499685 2.24611354]
[-0.17449621 2.18085941 0.9936368 ]
[ 2.23827935 1.02296045 -0.2612398 ]
[-0.34541291 1.11637043 2.22904248]
[ 0.96788879 2.12033521 -0.088224 ]
[-0.07704422 2.07965201 0.99739221]
[-0.3958175 1.23359604 2.16222145]
[ 2.13504156 1.01391343 -0.14895499]
[ 2.31059852 0.96260146 -0.27319998]
[ 2.22247594 1.07534695 -0.29782289]
[-0.27283046 1.13075432 2.14207614]
[-0.17449621 2.18085941 0.9936368 ]
[-0.29717239 0.92710063 2.37007176]
[ 2.33180515 1.03788212 -0.36968728]]
predict:
[2 1 0 1 2 1 0 1 1 1 2 0 2 0 0 1 2 2 1 2 1 2 2 1 2 2 1 2 2 2 1 0 1 1 1 1 1
2 0 0 2 1 0 0 2 0 1 1 0 1 2 1 0 2 2 2 2 0 0 2 2 0 2 0 1 2 0 0 2 0 0 0 1 2
2 0 0 0 1 2 0 0 2 0 2 1 2 2 0 1 0 2 0 0 2 0 2 1 1 1 2 2 2 2 0 1 2 1 0 2 1
1 2 0 0 0 2 1 2 0]
8.画图
N = 500
x1_min, x2_min = x.min()
x1_max, x2_max = x.max()
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, N)
x1, x2 = np.meshgrid(t1, t2) # 生成网格采样点
grid_show = np.dstack((x1.flat, x2.flat))[0] # 测试点
grid_hat = clf.predict(grid_show) # 预测分类值
grid_hat = grid_hat.reshape(x1.shape) # 使之与输入的形状相同
cm_light = mpl.colors.ListedColormap(['#00FFCC', '#FFA0A0', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
plt.figure(facecolor='w')
## 区域图
plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
## 所有样本点
plt.scatter(x[0], x[1], c=y, edgecolors='k', s=50, cmap=cm_dark) # 样本
## 测试数据集
plt.scatter(x_test[0], x_test[1], s=120, facecolors='none', zorder=10) # 圈中测试集样本
## lable列表
plt.xlabel(iris_feature[0], fontsize=13)
plt.ylabel(iris_feature[1], fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
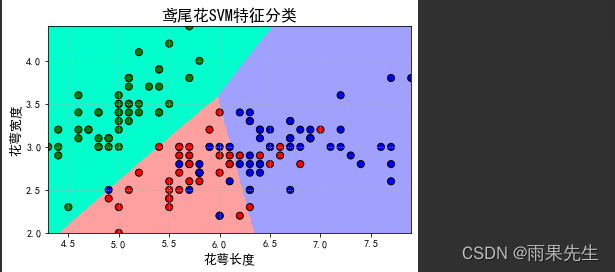
plt.title(u'鸢尾花SVM特征分类', fontsize=16)
plt.grid(b=True, ls=':')
plt.tight_layout(pad=1.5)
plt.show()
绘图显示
总结
提示:这里对文章进行总结:
以上就是今天要讲的内容,本文仅仅简单介绍了鸢尾花数据进行SVM分类,下一章将介绍02_案例二:鸢尾花数据不同分类器效果比较。