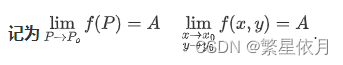高等数学笔记-乐经良老师
第八章 多元函数微分学(Ⅰ)
第一节 多元函数的基本概念
一、平面点集
01 邻域
- 点到点的距离
- 在二维空间中,点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0) 与 P 0 ( x 0 , y 0 ) P_0(x_0,y_0) P0(x0,y0) 的距离记为 d ( P , P 0 ) = ( x − x 0 ) 2 + ( y − y 0 ) 2 d\left(P, P_{0}\right)=\sqrt{\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}} d(P,P0)=(x−x0)2+(y−y0)2 .
-
δ
\delta
δ 邻域
- 集合 U ( P 0 , δ ) = { P ( x , y ) ∣ d ( P , P 0 ) < δ } U\left(P_{0}, \delta\right)=\left\{P(x, y) \mid d\left(P, P_{0}\right)<\delta\right\} U(P0,δ)={P(x,y)∣d(P,P0)<δ} 称为 P 0 P_0 P0 的 δ \delta δ 邻域 .
- 不强调半径时邻域为 U ( P 0 ) U(P_{0}) U(P0) .
- 去心
δ
\delta
δ 邻域
- 集合 U ∘ ( P 0 , P ) = { P ( x , y ) ∣ 0 < d ( P , P 0 ) < δ } \stackrel{\circ}{U}\left(P_{0}, P\right)=\left\{P(x, y) \mid 0<d\left(P, P_{0}\right)<\delta\right\} U∘(P0,P)={P(x,y)∣0<d(P,P0)<δ} 称为 P 0 P_0 P0 的去心 δ \delta δ 邻域 .
02 开集与区域
-
E E E 是平面 R 2 R^2 R2 中的集合, P 0 P_0 P0 是平面中的点.
-
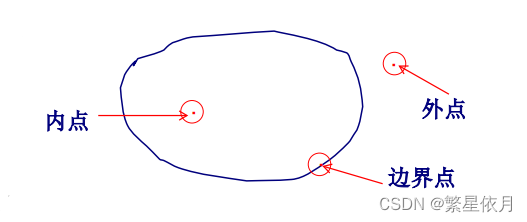
内点与边界点
-
内点
若 ∃ δ > 0 \exist \delta>0 ∃δ>0,使 U ( P 0 , δ ) ⊂ E U(P_{0},\delta) \subset E U(P0,δ)⊂E,称 P 0 P_0 P0 为 E E E 的内点.
-
边界点
若对 ∀ δ \forall \delta ∀δ,在 U ( P 0 , δ ) U(P_{0},\delta) U(P0,δ) 内既有属于 E E E 的点,又有不属于 E E E 的点,称 P 0 P_0 P0 为 E E E 的边界点.
-
-
开集与闭集
-
开集
若集合 E E E 中每个点都是 E E E 的内点,称 E E E 为开集 .
-
闭集
开集 E E E 的余集 R 2 − E R^2-E R2−E 称为闭集 .
-
-
连通与区域
-
连通
若集合 E E E 中任意两点都能用完全属于 E E E 的折线连接起来,则称 E E E 是连通的.
-
区域
连通的开集称为区域.
-
-
边界与闭区域
-
边界
E E E 的所有边界点组成的集合称为 E E E 的边界.
-
闭区域
区域连同其边界称为闭区域 .
-
-
有界
若存在 R R R,集合 E ⊂ { ( x , y ) ∣ x 2 + y 2 < R 2 } E \subset\left\{(x, y) \mid x^{2}+y^{2}<R^{2}\right\} E⊂{(x,y)∣x2+y2<R2},称 E E E 有界.
二、多元函数
-
多元函数的概念
-
多元函数
简单说,函数依赖的自变量多于一个称为多元函数.
-
二元函数
设 D D D 是平面的非空集, f f f 是 D → R D \rightarrow \mathbf{R} D→R 的映射,则称 f f f 是定义在 D D D 上的二元函数,记为 f : D → R f: D \rightarrow \mathbf{R} f:D→R 或者 z = f ( x , y ) , ( x , y ) ∈ D z=f(x, y), \quad(x, y) \in D z=f(x,y),(x,y)∈D .
-
二元函数两要素
与一元情况类似,二元函数包括两个要素:定义域、对应关系。
-
-
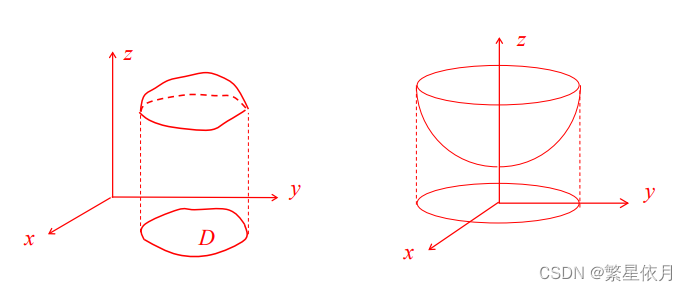
多元函数图形(图象)
- 集合 { ( x , y , z ) ∣ z = f ( x , y ) , ( x , y ) ∈ D } \{(x, y, z) \mid z=f(x, y),(x, y) \in D\} {(x,y,z)∣z=f(x,y),(x,y)∈D} 所对应几何图形称为二元函数的图形.
- 一般而言是 R 3 \mathrm{R}^{3} R3 中 的一个曲面.
- 曲面在
x
y
x y
xy 面上的投影区域就是函数的定义域
D
D
D .
-
第二节 多元函数的极限与连续
一、二元函数的极限
01 二元函数极限的概念
设二元函数定义在 P 0 P_{0} P0 点的去心邻域,若存在数 A A A, ∀ ε > 0 , ∃ δ > 0 \forall \varepsilon>0, \exists \delta>0 ∀ε>0,∃δ>0,
使得当 0 < d ( P , P 0 ) < δ 0<d\left(P, P_{0}\right)<\delta 0<d(P,P0)<δ 时, ∣ f ( P ) − A ∣ = ∣ f ( x , y ) − A ∣ < ε |f(P)-A|=|f(x, y)-A|<\varepsilon ∣f(P)−A∣=∣f(x,y)−A∣<ε,
则称当 P → P 0 P \rightarrow P_{0} P→P0 或 ( x , y ) → ( x 0 , y 0 ) (x, y) \rightarrow\left(x_{0}, y_{0}\right) (x,y)→(x0,y0) 时, f ( x , y ) f(x, y) f(x,y) 的极限为 A A A,
02 二元函数极限与一元函数极限的比较
- 类似点
- ( x , y ) (x, y) (x,y) 趋近点 ( x 0 , y 0 ) \left(x_{0}, y_{0}\right) (x0,y0) 时函数 f ( x , y ) f(x, y) f(x,y) 变化的定量趋势
- 计算多元函数极限时,等价代换、四则运算、夹逼准则等性质和定理仍成立
- 计算多元函数极限时,变量代换不能用,但极坐标变换可以用
- 区别点
- 平面上 P → P 0 P \rightarrow P_0 P→P0 有无穷多方向,且采取的路径也是任意的,既可取直线,也可取曲线 ( 任意趋近 ) ;
- 无论从何种方向或沿何种路径,只要 P P P 点与 P 0 P_0 P0 的距离充分小,都必须有 ∣ f ( P ) − A ∣ \mid f(P)-A \mid ∣f(P)−A∣ 充分小。
二、二元函数的连续性
01 二元函数连续性的概念
-
连续与连续点
若二元函数 f ( x , y ) f(x, y) f(x,y) 满足 lim ( x , y ) → ( x 0 , y 0 ) f ( x , y ) = f ( x 0 , y 0 ) \lim \limits_{(x, y) \rightarrow\left(x_{0}, y_{0}\right)} f(x, y)=f\left(x_{0}, y_{0}\right) (x,y)→(x0,y0)limf(x,y)=f(x0,y0),则称函数 f ( x , y ) f(x, y) f(x,y) 在 ( x 0 , y 0 ) \left(x_{0}, y_{0}\right) (x0,y0) 处连续,也称 ( x 0 , y 0 ) \left(x_{0}, y_{0}\right) (x0,y0) 是 f f f 的连续点.
-
间断
若不满足连续的条件(即不连续),则称为间断.
-
连续函数
若二元函数 f ( x , y ) f(x, y) f(x,y) 在平面区域 D D D 上每一点都连续,则称 f f f 在区域 D D D 上连续,或称 f f f 是 D D D 上的连续函数,记为 f ∈ C ( D ) f \in C(D) f∈C(D).
02 二元函数连续性的运算
- 二元连续函数的和差积商仍为连续函数,其复合函数是连续函数。
- 注意取商时分母不为零。
03 二元初等函数
- 二元初等函数在其定义域内都是连续的。
- 间断点在无定义的孤立点或者线处。
04 连续的全增量表示
- 全增量: Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0) Δz=f(x0+Δx,y0+Δy)−f(x0,y0)
- 连续的全增量表示: lim ( Δ x , Δ y ) → ( 0 , 0 ) Δ z = 0 \lim \limits_{(\Delta x,\Delta y) \rightarrow (0,0)} \Delta z=0 (Δx,Δy)→(0,0)limΔz=0
05 二元函数连续的表述
- 区域内连续:区域内每一点连续。
- 闭区域内连续:边界点连续。
03 闭区域上的二元连续函数的性质
- 与一元情况类似
- 有界性:闭区间的二元连续函数一定有界
- 最值性(最值可取)
- 介值性(介值定理)
第三节 偏导数
一、偏导数的概念
01 偏导数
对二元函数 f ( x , y ) f(x, y) f(x,y) 在点 ( x 0 , y 0 ) \left(x_{0}, y_{0}\right) (x0,y0) 给 x x x 以增量 Δ x \Delta x Δx,
相应地函数有增量 (偏增量) Δ x z = f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) \Delta_{x} z=f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right) Δxz=f(x0+Δx,y0)−f(x0,y0),
函数 f f f 在点 ( x 0 , y 0 ) \left(x_{0}, y_{0}\right) (x0,y0) 处对 x x x 的偏导数
f x ( x 0 , y 0 ) = lim Δ x → 0 Δ x z Δ x = lim Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x f_{x}\left(x_{0}, y_{0}\right)=\lim \limits_{\Delta x \rightarrow 0} \frac{\Delta_{x} z}{\Delta x}=\lim \limits_{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x, y_{0}\right)-f\left(x_{0}, y_{0}\right)}{\Delta x} fx(x0,y0)=Δx→0limΔxΔxz=Δx→0limΔxf(x0+Δx,y0)−f(x0,y0),
偏导数也可记为 ∂ f ∂ x ∣ ( x 0 , y 0 ) \left.\frac{\partial f}{\partial x}\right|_{\left(x_{0}, y_{0}\right)} ∂x∂f (x0,y0) .
02 偏导函数
函数 f f f 在区域 D D D 上每一点都存在偏导数,则这些偏导数是 D D D 上的二元函数,称为偏导函数,记为 f x ( x , y ) , f y ( x , y ) 或 ∂ f ∂ x ( x , y ) , ∂ f ∂ y ( x , y ) f_{x}(x, y), f_{y}(x, y) \text { 或 } \frac{\partial f}{\partial x}(x, y), \frac{\partial f}{\partial y}(x, y) fx(x,y),fy(x,y) 或 ∂x∂f(x,y),∂y∂f(x,y) .
二、偏导数的说明
- 对变量 y y y 的偏导数类似。
- 多元函数的偏导数是其对某一自变量的变化率。
三、二元函数偏导数求法
把 y y y 固定在 y 0 y_{0} y0,求一元函数 f ( x 0 , y 0 ) f\left(x_{0}, y_{0}\right) f(x0,y0) 在 x 0 x_{0} x0 处的导数,就得到偏导数 f x ( x 0 , y 0 ) f_{x}\left(x_{0}, y_{0}\right) fx(x0,y0),同样方法可以计算偏导数 f y ( x 0 , y 0 ) f_{y}\left(x_{0}, y_{0}\right) fy(x0,y0).
四、连续与可偏导的关系
01 可偏导未必连续
f ( x , y ) = { x y x 2 + y 2 ( x , y ) ≠ ( 0 , 0 ) 0 ( x , y ) = ( 0 , 0 ) f(x, y)=\left\{\begin{array}{cc}\frac{x y}{x^{2}+y^{2}} & (x, y) \neq(0,0) \\ 0 & (x, y)=(0,0)\end{array}\right. f(x,y)={x2+y2xy0(x,y)=(0,0)(x,y)=(0,0) 该函数在 ( 0 , 0 ) (0,0) (0,0) 的情况
02 连续未必可偏导
f ( x , y ) = ∣ x ∣ + ∣ y ∣ f(x, y)=|x|+|y| f(x,y)=∣x∣+∣y∣ 在 ( 0 , 0 ) (0,0) (0,0) 的情况
五、二元函数偏导数的几何意义
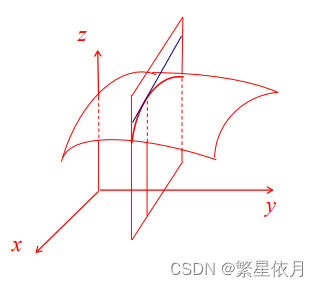
01 曲面与平面的交线
曲面 z = f ( x , y ) z=f(x, y) z=f(x,y) 与平面 y = y 0 y=y_{0} y=y0 的交线 { z = f ( x , y ) y = y 0 ⇒ z = f ( x , y 0 ) \begin{cases}z=f(x, y) \\ y=y_{0} \end{cases} \Rightarrow z=f\left(x, y_{0}\right) {z=f(x,y)y=y0⇒z=f(x,y0) (平面 y = y 0 y=y_0 y=y0上的曲线)
02 切线关于坐标轴的斜率
f x ( x 0 , y 0 ) f_x(x_0,y_0) fx(x0,y0) 是上述曲线在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0) 点处的切线关于 x x x 轴的斜率
六、高阶偏导数
01 高阶偏导数的概念
(1) 二阶偏导数
f
(
x
,
y
)
f(x, y)
f(x,y) 在
(
x
0
,
y
0
)
\left(x_{0}, y_{0}\right)
(x0,y0) 的邻域内的偏导数
f
x
(
x
,
y
)
,
f
y
(
x
,
y
)
f_{\mathrm{x}}(x, y),f_{y}(x, y)
fx(x,y),fy(x,y) 的偏导数称为
f
f
f 在
(
x
0
,
y
0
)
\left(x_{0}, y_{0}\right)
(x0,y0) 点处的二阶偏导数
f
x
x
=
∂
2
f
∂
x
2
=
∂
∂
x
(
∂
f
∂
x
)
f
x
y
=
∂
2
f
∂
x
∂
y
=
∂
∂
y
(
∂
f
∂
x
)
f
y
x
=
∂
2
f
∂
y
∂
x
=
∂
∂
x
(
∂
f
∂
y
)
f
y
y
=
∂
2
f
∂
y
2
=
∂
∂
y
(
∂
f
∂
y
)
\begin{aligned} f_{x x} &=\frac{\partial^{2} f}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right) & f_{x y}=\frac{\partial^{2} f}{\partial x \partial y}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right) \\ f_{y x} &=\frac{\partial^{2} f}{\partial y \partial x}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right) & f_{y y}=\frac{\partial^{2} f}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right) \end{aligned}
fxxfyx=∂x2∂2f=∂x∂(∂x∂f)=∂y∂x∂2f=∂x∂(∂y∂f)fxy=∂x∂y∂2f=∂y∂(∂x∂f)fyy=∂y2∂2f=∂y∂(∂y∂f)
(2) 三阶偏导数
类似地,二阶偏导数的偏导数为三阶偏导数,例如 f x x y = ∂ 3 f ∂ x 2 ∂ y = ∂ ∂ y ( ∂ 2 f ∂ x 2 ) f_{x x y}=\frac{\partial^{3} f}{\partial x^{2} \partial y}=\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial x^{2}}\right) fxxy=∂x2∂y∂3f=∂y∂(∂x2∂2f) .
02 混合偏导数
- 对于函数的高阶偏导数,对每一阶偏导数求导时,并不只针对同一个自变量,这样的偏导数称为混合偏导数。
- 混合偏导数并不总与求导次序无关。
- 混合偏导数与求导次序无关的充分条件(二元函数二阶混合偏导数相等定理)
- 若函数 f ( x , y ) f(x, y) f(x,y) 的两个二阶混合偏导数在点 ( x , y ) (x, y) (x,y) 连续,则 f x y ( x , y ) = f y x ( y , x ) f_{x y}(x, y)=f_{y x}(y, x) fxy(x,y)=fyx(y,x) .
第四节 全微分
一、全微分的概念
00 回顾一元函数
若 Δ f = A ⋅ Δ x + o ( Δ x ) \Delta f=A \cdot \Delta x+o(\Delta x) Δf=A⋅Δx+o(Δx),微分 d f = A ⋅ Δ x d f=A \cdot \Delta x df=A⋅Δx 是增量 Δ f \Delta f Δf 在 x 0 x_{0} x0 的线性主部。
01 全增量
对函数 z = f ( x , y ) \mathrm{z}=f(x, y) z=f(x,y),称 Δ z = Δ f = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=\Delta f=f\left(x_{0}+\Delta x, y_{0}+\Delta y\right)-f\left(x_{0}, y_{0}\right) Δz=Δf=f(x0+Δx,y0+Δy)−f(x0,y0) 为函数 z z z 的全增量。
02 可微
对函数 z = f ( x , y ) \mathrm{z}=f(x, y) z=f(x,y),若全增量 Δ z = Δ f = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=\Delta f=f\left(x_{0}+\Delta x, y_{0}+\Delta y\right)-f\left(x_{0}, y_{0}\right) Δz=Δf=f(x0+Δx,y0+Δy)−f(x0,y0)
可写为 Δ z = A ⋅ Δ x + B ⋅ Δ y + o ( ρ ) \Delta z=A \cdot \Delta x+B \cdot \Delta y+o(\rho) Δz=A⋅Δx+B⋅Δy+o(ρ) ( A A A, B B B 为常数, ρ = ( Δ x ) 2 + ( Δ y ) 2 \rho=\sqrt{(\Delta x)^{2}+(\Delta y)^{2}} ρ=(Δx)2+(Δy)2),
则称 f f f 在 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 可微。
03 全微分
而其中 A ⋅ Δ x + B ⋅ Δ y A \cdot \Delta x+B \cdot \Delta y A⋅Δx+B⋅Δy 为函数 f f f 在 P 0 ( x 0 , y 0 ) P_{0}\left(x_{0}, y_{0}\right) P0(x0,y0) 点处的全微分,
记为 d z ∣ ( x 0 , y 0 ) = d f ∣ ( x 0 , y 0 ) = A ⋅ Δ x + B ⋅ Δ y \left.d z\right|_{\left(x_{0}, y_{0}\right)}=\left.d f\right|_{\left(x_{0}, y_{0}\right)}=A \cdot \Delta x+B \cdot \Delta y dz∣(x0,y0)=df∣(x0,y0)=A⋅Δx+B⋅Δy (增量 Δ f \Delta f Δf 的线性主部)
04 可微函数
若 f ( x , y ) f(x,y) f(x,y) 在区域 D D D 每点处都可微,则称 f f f 是 D D D 内的可微函数。
二、可微与连续及可偏导的关系
01 可微必连续
02 可微必可偏导
函数 f f f 有 d f ∣ ( x 0 , y 0 ) = A ⋅ Δ x + B ⋅ Δ y ⇒ f x ( x 0 , y 0 ) = A , f y ( x 0 , y 0 ) = B \left.d f\right|_{\left(x_{0}, y_{0}\right)}=A \cdot \Delta x+B \cdot \Delta y \Rightarrow f_{x}\left(x_{0}, y_{0}\right)=A, f_{y}\left(x_{0}, y_{0}\right)=B df∣(x0,y0)=A⋅Δx+B⋅Δy⇒fx(x0,y0)=A,fy(x0,y0)=B
由 d x = Δ x , d y = Δ y d x=\Delta x, d y=\Delta y dx=Δx,dy=Δy 得到 d z = f x ( x , y ) d x + f y ( x , y ) d y d z=f_{x}(x, y) d x+f_{y}(x, y) d y dz=fx(x,y)dx+fy(x,y)dy
03 有连续偏导数则可微
偏导数连续 ⇒ \Rightarrow ⇒ 可微 ⇒ { 连续 ↑ × × ↓ 可偏导 \Rightarrow\left\{\begin{array}{l}\text { 连续 } \\ \ \stackrel{×}{\uparrow} \stackrel{\downarrow}{×} \\ \text { 可偏导 }\end{array}\right. ⇒⎩ ⎨ ⎧ 连续 ↑××↓ 可偏导
三、全微分的几何意义
微分 A ⋅ Δ x + B ⋅ Δ y A \cdot \Delta x+B \cdot \Delta y A⋅Δx+B⋅Δy 是 Δ z = f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) \Delta z=f\left(x_{0}+\Delta x, y_{0}+\Delta y\right)-f\left(x_{0}, y_{0}\right) Δz=f(x0+Δx,y0+Δy)−f(x0,y0) 的线性主部,这意味着可用 A ( x − x 0 ) + B ( y − y 0 ) A\left(x-x_{0}\right)+B\left(y-y_{0}\right) A(x−x0)+B(y−y0) 近似 Δ z = f ( x , y ) − f ( x 0 , y 0 ) \Delta z=f(x, y)-f\left(x_{0}, y_{0}\right) Δz=f(x,y)−f(x0,y0) .
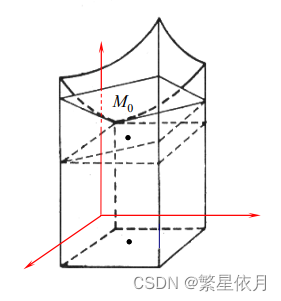
从几何上看,微分就是在就是在点 M 0 ( x 0 , y 0 ) M_{0}\left(x_{0}, y_{0}\right) M0(x0,y0) 的附近存在近似曲面的平面, z − z 0 = A ( x − x 0 ) + B ( y − y 0 ) z-z_{0}=A\left(x-x_{0}\right)+B\left(y-y_{0}\right) z−z0=A(x−x0)+B(y−y0) 实际上是曲面的切平面。
四、全微分的应用
近似 Δ z ≈ d z = f x ( x 0 , y 0 ) Δ x + f y ( x 0 , y 0 ) Δ y \Delta z \approx d z=f_{x}\left(x_{0}, y_{0}\right) \Delta x+f_{y}\left(x_{0}, y_{0}\right) \Delta y Δz≈dz=fx(x0,y0)Δx+fy(x0,y0)Δy
全微分可以用于近似计算
最后
😊为防止河蟹,链接已经通过“与熊论道/熊曰加密”加密处理,将下面的文字复制到“与熊论道/熊曰加密”页面的第二个输入框,点击“领悟熊所言的真谛”即可查看链接啦:
😊熊曰:呋食食呦蜜非象嗚家吃呱山萌萌笨有哞魚既魚性蜜覺呆食哮性洞哮山噗眠嗥嚄萌洞擊嗄襲呱物人你
😊如果嫌麻烦的话请私信咨询博主,谢谢!
😊PS:繁星依月/惟欢/一舟均为博主的马甲,本篇作品完全原创,再次感谢!