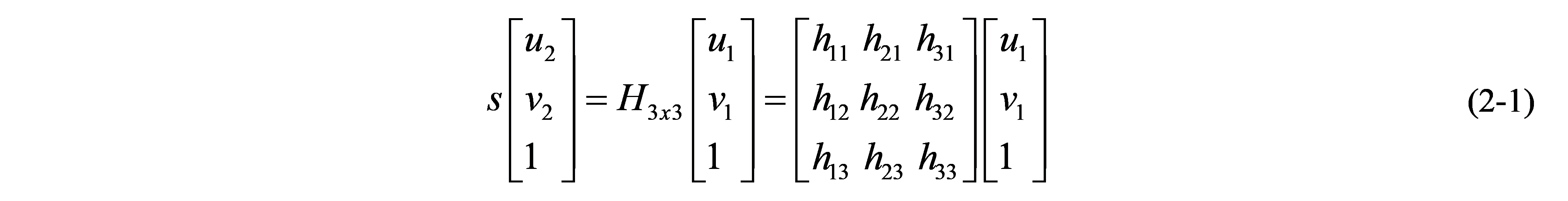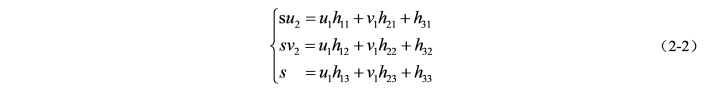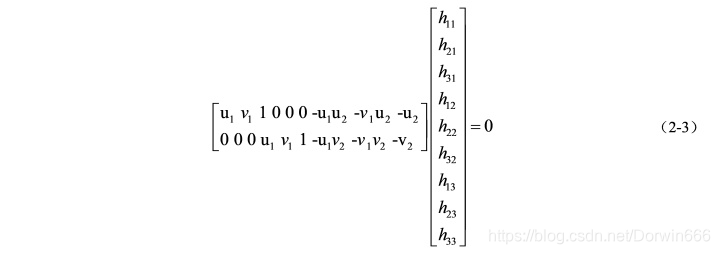【转载】Apriltag定位和识别
目录
- 前言
- 定位
- 图像分割
- 轮廓查找
- 寻找四边形
- 单应变换
- 解码
本文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
1. 前言
Apriltag 作为一种视觉定位标志符,类似于二维码或者条形码。需要一种特定的算法来实现高精度、高鲁棒性的定位;需要一套独特的编解码系统来做唯一识别。
Apriltag 解码算法的主要步骤如下:
1、自适应阈值分割
2、查找轮廓,使用 Union-find 查找连通域
3、对轮廓进行直线拟合,查找候选的凸四边形
4、对四边形进行解码,识别 Tag
5、坐标变换,转换到世界坐标系
2. 定位
定位这个事,挺麻烦的。条条大路通罗马,apriltag 实验室从 2011 年到至今,搞了 3 个定位版本出来,其中修修补补的小事更加多,只是为了更加鲁棒、高效。本文只对 2016 年的论文进行分析。
怎么从复杂场景中定位出 apriltag 的位置呢。图像处理的美妙之处是你总能找到一种组合路径来分割出目标。图像分割的传统算法种类繁多,最基础的就是阈值分割、色彩分割、基于图的分割。Apritag 的检测也不例外。
3. 图像分割
2016 年的论文里面是采用的自适应阈值进行图像分割,主要考虑了光照不均和黑暗照明对图像的影响,提高分割的准确性。自适应阈值的主要思想就是在像素领域内寻找一个合理的阈值进行分割,选取灰度均值和中值都是常见的手法。在这个基础又重要的步骤,作者采用了一个 trick,先将图像进行 4x4 网格分块,求出每个分块的灰度最大值和最小值,然后对所有分块计算的最大最小灰度值进行一个 3 邻域最大最小滤波处理,将滤波后的最大最小均值 ((max+min)/2) 作为分块区域的阈值。分块的目的主要是增加鲁棒性,区域的特征总比单一像素的更加稳定,减少随机噪声的干扰,同时提升计算效率。
4. 轮廓查找
通过自适应阈值后,得到一张二值图像。接下来就是要寻找可能组成 tag 标志的轮廓。连通域查找的简单方法就是计算二值图像中的黑白边缘,但是这样查找的连通域很容易出现两个 tag 公用一条边时导致连通域查找错误。因此作者采用了 union-find 算法来求连通域,每个连通域都有一个唯一的 ID。
5. 寻找四边形
轮廓有了之后,对每一个轮廓进行分割,产生一个残差最小的凸四边形,作为 tag 位置的候选。这其中最难的是找四边形的四个顶点,如果对于规则的正方形或者矩形来说,其实是相对比较好做的。但是存在 tag 存在变形和仿射变化时,就有点难了。首先对无序的轮廓点按照对重心的角度进行排序,这绝对是一个很棒的 ideal。有了排序的轮廓点,然后就是按部就班的按照顺序选取距离中心点一定范围内的点进行直线拟合,不断迭代索引,计算每条直线的误差总和;对误差总和进行一个低通滤波,使系统更加鲁棒,然后选取误差总和最大的四条直线对应的角点索引作为四边形角点。然后取角点间的点拟合直线,求得四条直线的角点作为 Tag 的顶点。(这部分是最耗时的,类似于穷举,虽然是拟合直线,但是次数非常多,需重点优化的部分)。
为了得到更高精度的角点坐标,需要尽可能找到真正的梯度边缘直线。因此对直线上的点进行采样,然后计算搜索采样点在直法向量上梯度最大的点,作为最后进行直线拟合的点(图像真正的梯度边缘)。
在众多的四边形中,需要按照 Apriltag 的实际几何特征来过滤明显异常的四边形,比如四边形边长比例不能差的太多,两条相邻边的角度不能离 90 度太远之类的,这就是一些常用异常处理手段,最后筛选出的候选码如下,见图 6(选了一张效果和原算法有些差异的图片,可以看出不同算法的差异)。
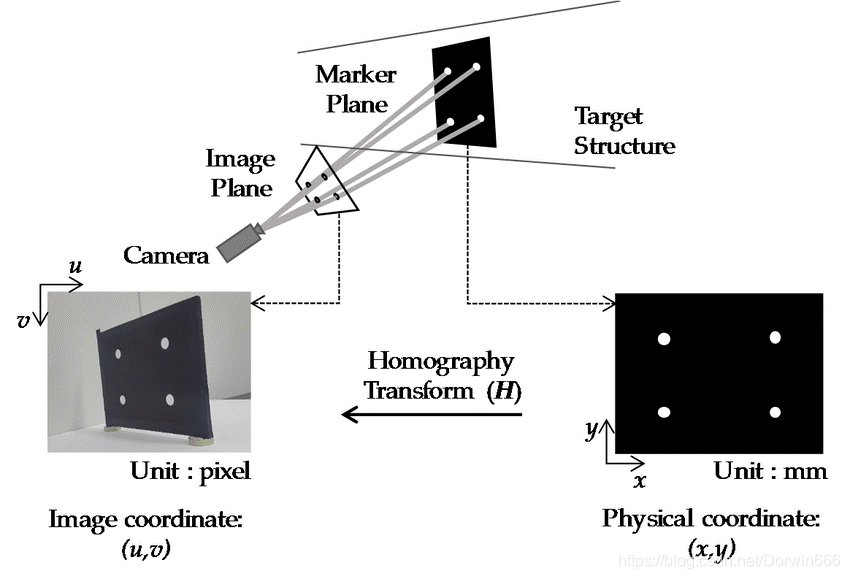
6. 单应变换
找到的四边形大概率存在仿射变换(单应变换特殊情况),很难找到规则正方形,因此需要将图像投影成完全符合理论上的正方形,此处就涉及到单应变。一是为了解码的需要,二是为了求解姿态。
背后的数学原理很简单(详见多目几何第二版),就是求解对应点之间的一个坐标变换。对于每一个对应的点对,都应该存在如下关系(公式 2-1),理论点坐标等于变换矩阵乘以实际图像点坐标。
将公式(2-1)展开得到公式(2-2):
进一步变换,消去尺度因子 s,并将 H 矩阵的元素看做一个列向量,可得到公式(2-3),是不是很熟悉 AX = 0:
因为存在尺度因子的影响,H 矩阵最后一个元素可以归一化成 1,因此 H 矩阵的自由度为 8。为了得到公式(2-3)的解,至少需要 4 个点对,采用直接线性化可以求出上述方程,得到单应矩阵 H。
四边形内的每一个点通过上述变换,都能计算出在理论矩形下的唯一坐标(注意尺度的影响),然后可以按照解码规则进行解码。
已知相机内参和世界坐标与图像之间的单应矩阵 H,求解相机外参,即 Apriltag 在世界坐标下的位姿。详细推导见我司的另一篇文章(计算机视觉基础—相机标定 2.1 节),传送门 https://zhuanlan.zhihu.com/p/87334006。
7. 解码
编解码方法是 Apriltag 团队研究出来的,属于特定的方法,我们可以改变的地方不大,因此不做具体解释。想深度了解的,可以查阅 Apriltag 编解码资料。通过识别固定类型的码型,可进一步排除其他码型的干扰,得到最终的结果。