文章目录
一、什么是数据结构?
定义
在计算机科学领域,数据结构是一种数据组织、管理和存储格式,通常被选择用来高效访问数据。
数据结构是一种存储和组织数据的方式,旨在便于访问和修改
可以说,程序 = 数据结构 + 算法,它们是每一位程序员的基本功。
二、递归
1) 概述
定义
计算机科学中,递归是一种解决计算问题的方法,其中解决方案取决于同一类问题的更小子集
比如单链表递归遍历的例子:
void f(Node node) {
if(node == null) {
return;
}
println("before:" + node.value)
f(node.next);
println("after:" + node.value)
}
说明:
- 自己调用自己,如果说每个函数对应着一种解决方案,自己调用自己意味着解决方案是一样的(有规律的)
- 每次调用,函数处理的数据会较上次缩减(子集),而且最后会缩减至无需继续递归
- 内层函数调用(子集处理)完成,外层函数才能算调用完成
原理
假设链表中有 3 个节点,value 分别为 1,2,3,以上代码的执行流程就类似于下面的伪码
// 1 -> 2 -> 3 -> null f(1)
void f(Node node = 1) {
println("before:" + node.value) // 1
void f(Node node = 2) {
println("before:" + node.value) // 2
void f(Node node = 3) {
println("before:" + node.value) // 3
void f(Node node = null) {
if(node == null) {
return;
}
}
println("after:" + node.value) // 3
}
println("after:" + node.value) // 2
}
println("after:" + node.value) // 1
}
- 深入到最里层叫做递
- 从最里层出来叫做归
- 在递的过程中,外层函数内的局部变量(以及方法参数)并未消失,归的时候还可以用到
2) 单路递归 Single Recursion
E01. 阶乘
用递归方法求阶乘
-
阶乘的定义 n ! = 1 ⋅ 2 ⋅ 3 ⋯ ( n − 2 ) ⋅ ( n − 1 ) ⋅ n n!= 1⋅2⋅3⋯(n-2)⋅(n-1)⋅n n!=1⋅2⋅3⋯(n−2)⋅(n−1)⋅n,其中 n n n 为自然数,当然 0 ! = 1 0! = 1 0!=1
-
递推关系
f ( n ) = { 1 n = 1 n ∗ f ( n − 1 ) n > 1 f(n) = \begin{cases} 1 & n = 1\\ n * f(n-1) & n > 1 \end{cases} f(n)={1n∗f(n−1)n=1n>1
代码
// TODO 递归
public int f(int n){
if (n == 1){
return 1;
}else {
return n * f(n - 1);
}
}
@Test
public void f () {
Factorial f = new Factorial();
System.out.println(f.f(5));
}
拆解伪码如下,假设 n 初始值为 3
f(int n = 3) { // 解决不了,递
return 3 * f(int n = 2) { // 解决不了,继续递
return 2 * f(int n = 1) {
if (n == 1) { // 可以解决, 开始归
return 1;
}
}
}
}
E02. 反向打印字符串
用递归反向打印字符串,n 为字符在整个字符串 str 中的索引位置
- 递:n 从 0 开始,每次 n + 1,一直递到 n == str.length() - 1
- 归:从 n == str.length() 开始归,从归打印,自然是逆序的
递推关系
f
(
n
)
=
{
停止
n
=
s
t
r
.
l
e
n
g
t
h
(
)
f
(
n
+
1
)
0
≤
n
≤
s
t
r
.
l
e
n
g
t
h
(
)
−
1
f(n) = \begin{cases} 停止 & n = str.length() \\ f(n+1) & 0 \leq n \leq str.length() - 1 \end{cases}
f(n)={停止f(n+1)n=str.length()0≤n≤str.length()−1
代码为
// TODO 字符串递归
public static void f2(int n,String str){
if (n==str.length()){
return;
}
System.out.println(str.charAt(n));
f2(n+1,str);
}
@Test
public void f2 () {
Factorial.f2(5,"abcdefghigkhmnopqrstvuwxyz");
}
E03. 二分查找(单路递归)
// TODO 二分查找递归
public static int f3 (int[]a,int target,int i,int j){
if(i>j){
return -1;
}
int m =i+j>>>1;
if(a[m]<target){
return f3(a,target,m+1,j);
} else if (a[m]>target) {
return f3(a,target,i,m-1);
}else {
return m;
}
}
@Test
public void f3 () {
int[] a = {1,2,3,4,5};
Factorial.f3(a,4,0,a.length-1);
}
E04. 冒泡排序(单路递归)
// TODO 冒泡排序
public static void f4(int[]a,int j){
if (j==0){
return;
}
for (int i = 0; i < j; i++) {
if (a[i]>a[j]){
int t =a[j];
a[j] = a[i];
a[i] = t;
}
}
f4(a,j-1);
}
@Test
public void f4 () {
int[] a = {9,8,7,6,5,4,3,2,1};
Factorial.f4(a,a.length-1);
System.out.println(Arrays.toString(a));
}
// TODO 冒泡排序2
public static void f5(int[] a,int x){
/*
x 为待排序列的右边界
* */
if(x==0){
return;
}
for (int i = 0, j = x; i < j; i++) {
if (a[i]>a[x]){
int t =a[x];
a[x] = a[i];
a[i] = t;
x=i;
}
}
f5(a,x);
}
@Test
public void f5 () {
int[] a = {9,8,7,6,5,4,3,2,1};
Factorial.f5(a,a.length-1);
System.out.println(Arrays.toString(a));
}
E05. 插入排序(单路递归)
// TODO 插入排序递归
public static void f6(int[] a,int low){
/*
low 未排序列的左边界
t 待插入元素
* */
if (low==a.length){
return;
}
int t = a[low];
int i = low-1;
while (i>=0&&t<a[i]){
a[i+1]=a[i];
i--;
}
a[i+1]=t;
f6(a,low+1);
return;
}
@Test
public void f6 () {
int[] a = {9,8,7,6,5,4,3,2,1};
Factorial.f6(a,0);
System.out.println(Arrays.toString(a));
}
- 已排序区域:[0 … i … low-1]
- 未排序区域:[low … high]
- 视频中讲解的是只考虑 low 边界的情况,参考以上代码,理解 low-1 … high 范围内的处理方法
- 扩展:利用二分查找 leftmost 版本,改进寻找插入位置的代码
3) 多路递归 Multi Recursion
E01. 斐波那契数列-Leetcode 70
- 之前的例子是每个递归函数只包含一个自身的调用,这称之为 single recursion
- 如果每个递归函数例包含多个自身调用,称之为 multi recursion
递推关系
f
(
n
)
=
{
0
n
=
0
1
n
=
1
f
(
n
−
1
)
+
f
(
n
−
2
)
n
>
1
f(n) = \begin{cases} 0 & n=0 \\ 1 & n=1 \\ f(n-1) + f(n-2) & n>1 \end{cases}
f(n)=⎩
⎨
⎧01f(n−1)+f(n−2)n=0n=1n>1
下面的表格列出了数列的前几项
| F0 | F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
实现
// TODO 斐波那契数列
public static int f7(int n){
if (n==0){
return 0;
}else if (n==1){
return 1;
}
int x = f7(n-1);
int y = f7(n-2);
return x+y;
}
@Test
public void f7 () {
System.out.println(Factorial.f7(10));
}
时间复杂度
- 递归的次数也符合斐波那契规律, 2 ∗ f ( n + 1 ) − 1 2 * f(n+1)-1 2∗f(n+1)−1
- 时间复杂度推导过程
- 斐波那契通项公式 f ( n ) = 1 5 ∗ ( 1 + 5 2 n − 1 − 5 2 n ) f(n) = \frac{1}{\sqrt{5}}*({\frac{1+\sqrt{5}}{2}}^n - {\frac{1-\sqrt{5}}{2}}^n) f(n)=51∗(21+5n−21−5n)
- 简化为: f ( n ) = 1 2.236 ∗ ( 1.618 n − ( − 0.618 ) n ) f(n) = \frac{1}{2.236}*({1.618}^n - {(-0.618)}^n) f(n)=2.2361∗(1.618n−(−0.618)n)
- 带入递归次数公式 2 ∗ 1 2.236 ∗ ( 1.618 n + 1 − ( − 0.618 ) n + 1 ) − 1 2*\frac{1}{2.236}*({1.618}^{n+1} - {(-0.618)}^{n+1})-1 2∗2.2361∗(1.618n+1−(−0.618)n+1)−1
- 时间复杂度为 Θ ( 1.61 8 n ) \Theta(1.618^n) Θ(1.618n)
E02. 兔子问题
变体1 - 兔子问题[^8]
- 第一个月,有一对未成熟的兔子(黑色,注意图中个头较小)
- 第二个月,它们成熟
- 第三个月,它们能产下一对新的小兔子(蓝色)
- 所有兔子遵循相同规律,求第 n n n 个月的兔子数
分析
兔子问题如何与斐波那契联系起来呢?设第 n 个月兔子数为 f ( n ) f(n) f(n)
- f ( n ) f(n) f(n) = 上个月兔子数 + 新生的小兔子数
- 而【新生的小兔子数】实际就是【上个月成熟的兔子数】
- 因为需要一个月兔子就成熟,所以【上个月成熟的兔子数】也就是【上上个月的兔子数】
- 上个月兔子数,即 f ( n − 1 ) f(n-1) f(n−1)
- 上上个月的兔子数,即 f ( n − 2 ) f(n-2) f(n−2)
因此本质还是斐波那契数列,只是从其第一项开始
实现
// TODO 斐波那契数列 兔子问题
public static int f8(int n){
return f7(n)*2;
}
@Test
public void f8 () {
System.out.println(Factorial.f8(10));
}
E03. 青蛙爬楼梯
变体2 - 青蛙爬楼梯
- 楼梯有 n n n 阶
- 青蛙要爬到楼顶,可以一次跳一阶,也可以一次跳两阶
- 只能向上跳,问有多少种跳法
分析
| n | 跳法 | 规律 |
|---|---|---|
| 1 | (1) | 暂时看不出 |
| 2 | (1,1) (2) | 暂时看不出 |
| 3 | (1,1,1) (1,2) (2,1) | 暂时看不出 |
| 4 | (1,1,1,1) (1,2,1) (2,1,1) (1,1,2) (2,2) | 最后一跳,跳一个台阶的,基于f(3) 最后一跳,跳两个台阶的,基于f(2) |
| 5 | … | … |
-
因此本质上还是斐波那契数列,只是从其第二项开始
-
对应 leetcode 题目 70. 爬楼梯 - 力扣(LeetCode)
实现
// TODO 斐波那契数列 青蛙问题
public static int f9(int n){
return f7(n+1);
}
@Test
public void f9 () {
System.out.println(Factorial.f9(10));
}
E04. 斐波那契数列-备忘录法
// TODO 递归求斐波那契数列
/*
* 备忘录法减少重复计算
* */
public static int f10(int n){
int[] cache = new int[n+1];
Arrays.fill(cache,-1);
cache[0]=0;
cache[1]=1;
return f11(n,cache);
}
public static int f11(int n,int[] cache){
if(cache[n]!=-1){
return cache[n];
}
cache[n]=f11(n-1,cache)+f11(n-2,cache);
return cache[n];
}
@Test
public void f10 () {
System.out.println(Factorial.f10(30));
}
三、递归案例题
汉诺塔
Tower of Hanoi,是一个源于印度古老传说:大梵天创建世界时做了三根金刚石柱,在一根柱子从下往上按大小顺序摞着 64 片黄金圆盘,大梵天命令婆罗门把圆盘重新摆放在另一根柱子上,并且规定
- 一次只能移动一个圆盘
- 小圆盘上不能放大圆盘
下面的动图演示了4片圆盘的移动方法
使用程序代码模拟圆盘的移动过程,并估算出时间复杂度
思路
-
假设每根柱子标号 a,b,c,每个圆盘用 1,2,3 … 表示其大小,圆盘初始在 a,要移动到的目标是 c
-
如果只有一个圆盘,此时是最小问题,可以直接求解
- 移动圆盘1 a ↦ c a \mapsto c a↦c
-
如果有两个圆盘,那么
- 圆盘1 a ↦ b a \mapsto b a↦b
- 圆盘2 a ↦ c a \mapsto c a↦c
- 圆盘1 b ↦ c b \mapsto c b↦c
-
如果有三个圆盘,那么
- 圆盘12 a ↦ b a \mapsto b a↦b
- 圆盘3 a ↦ c a \mapsto c a↦c
- 圆盘12 b ↦ c b \mapsto c b↦c
-
如果有四个圆盘,那么
- 圆盘 123 a ↦ b a \mapsto b a↦b
- 圆盘4 a ↦ c a \mapsto c a↦c
- 圆盘 123 b ↦ c b \mapsto c b↦c

题解
public static void main(String[] args) {
LinkedList<Integer> A = new LinkedList<>();
LinkedList<Integer> B = new LinkedList<>();
LinkedList<Integer> C = new LinkedList<>();
A.add(3);
A.add(2);
A.add(1);
hanota(A,B,C);
}
public static void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
move(A.size(),A,B,C);
System.out.println(C);
}
public static void move(int n, List<Integer> A, List<Integer> B, List<Integer> C){
if (n == 1){
C.add(A.remove(A.size()-1));
return;
}
move(n-1,A,C,B);
C.add(A.remove(A.size()-1));
move(n-1,B,A,C);
}
杨辉三角
分析
把它斜着看
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
- 行 i i i,列 j j j,那么 [ i ] [ j ] [i][j] [i][j] 的取值应为 [ i − 1 ] [ j − 1 ] + [ i − 1 ] [ j ] [i-1][j-1] + [i-1][j] [i−1][j−1]+[i−1][j]
- 当 j = 0 j=0 j=0 或 i = j i=j i=j 时, [ i ] [ j ] [i][j] [i][j] 取值为 1 1 1
题解
public static void main(String[] args) {
init(8);
}
//创建
public static void init(int n){
int[][] a = new int[n][n];
for (int i = 0; i < n; i++) {
for (int j = 0; j < (n-i-1)*2; j++) {
System.out.print(" ");
}
for (int j = 0; j <= i; j++) {
System.out.printf("%-4d",f(i,j));
}
System.out.println();
}
}
public static int f(int i,int j){
if (i==j||j==0) {
return 1;
}
return f(i-1,j-1)+f(i-1,j);
}
四、时间空间复杂度
1)时间复杂度
计算机科学中,时间复杂度是用来衡量:一个算法的执行,随数据规模增大,而增长的时间成本
- 不依赖于环境因素
如何表示时间复杂度呢?
-
假设算法要处理的数据规模是 n n n,代码总的执行行数用函数 f ( n ) f(n) f(n) 来表示,例如:
- 线性查找算法的函数 f ( n ) = 3 ∗ n + 3 f(n) = 3*n + 3 f(n)=3∗n+3
- 二分查找算法的函数 f ( n ) = ( f l o o r ( l o g 2 ( n ) ) + 1 ) ∗ 5 + 4 f(n) = (floor(log_2(n)) + 1) * 5 + 4 f(n)=(floor(log2(n))+1)∗5+4
-
为了对 f ( n ) f(n) f(n) 进行化简,应当抓住主要矛盾,找到一个变化趋势与之相近的表示法
渐进上界
渐进上界(asymptotic upper bound):从某个常数 n 0 n_0 n0开始, c ∗ g ( n ) c*g(n) c∗g(n) 总是位于 f ( n ) f(n) f(n) 上方,那么记作 O ( g ( n ) ) O(g(n)) O(g(n))
- 代表算法执行的最差情况
例1
- f ( n ) = 3 ∗ n + 3 f(n) = 3*n+3 f(n)=3∗n+3
- g ( n ) = n g(n) = n g(n)=n
- 取 c = 4 c=4 c=4,在 n 0 = 3 n_0=3 n0=3 之后, g ( n ) g(n) g(n) 可以作为 f ( n ) f(n) f(n) 的渐进上界,因此表示法写作 O ( n ) O(n) O(n)
例2
- f ( n ) = 5 ∗ f l o o r ( l o g 2 ( n ) ) + 9 f(n) = 5*floor(log_2(n)) + 9 f(n)=5∗floor(log2(n))+9
- g ( n ) = l o g 2 ( n ) g(n) = log_2(n) g(n)=log2(n)
- O ( l o g 2 ( n ) ) O(log_2(n)) O(log2(n))
已知 f ( n ) f(n) f(n) 来说,求 g ( n ) g(n) g(n)
- 表达式中相乘的常量,可以省略,如
- f ( n ) = 100 ∗ n 2 f(n) = 100*n^2 f(n)=100∗n2 中的 100 100 100
- 多项式中数量规模更小(低次项)的表达式,如
- f ( n ) = n 2 + n f(n)=n^2+n f(n)=n2+n 中的 n n n
- f ( n ) = n 3 + n 2 f(n) = n^3 + n^2 f(n)=n3+n2 中的 n 2 n^2 n2
- 不同底数的对数,渐进上界可以用一个对数函数
log
n
\log n
logn 表示
- 例如: l o g 2 ( n ) log_2(n) log2(n) 可以替换为 l o g 10 ( n ) log_{10}(n) log10(n),因为 l o g 2 ( n ) = l o g 10 ( n ) l o g 10 ( 2 ) log_2(n) = \frac{log_{10}(n)}{log_{10}(2)} log2(n)=log10(2)log10(n),相乘的常量 1 l o g 10 ( 2 ) \frac{1}{log_{10}(2)} log10(2)1 可以省略
- 类似的,对数的常数次幂可省略
- 如: l o g ( n c ) = c ∗ l o g ( n ) log(n^c) = c * log(n) log(nc)=c∗log(n)
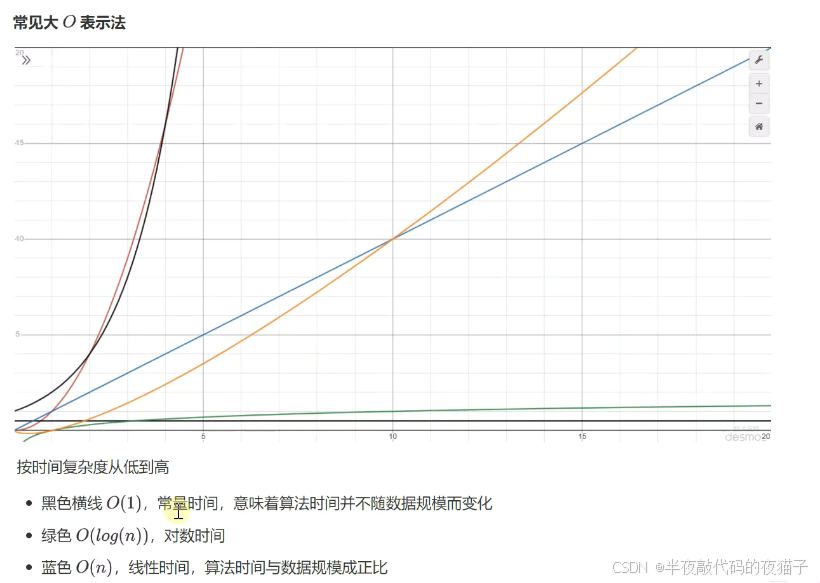
常见大 O O O 表示法
按时间复杂度从低到高
- 黑色横线 O ( 1 ) O(1) O(1),常量时间,意味着算法时间并不随数据规模而变化
- 绿色 O ( l o g ( n ) ) O(log(n)) O(log(n)),对数时间
- 蓝色 O ( n ) O(n) O(n),线性时间,算法时间与数据规模成正比
- 橙色 O ( n ∗ l o g ( n ) ) O(n*log(n)) O(n∗log(n)),拟线性时间
- 红色 O ( n 2 ) O(n^2) O(n2) 平方时间
- 黑色朝上 O ( 2 n ) O(2^n) O(2n) 指数时间
- 没画出来的 O ( n ! ) O(n!) O(n!)
渐进下界
渐进下界(asymptotic lower bound):从某个常数 n 0 n_0 n0开始, c ∗ g ( n ) c*g(n) c∗g(n) 总是位于 f ( n ) f(n) f(n) 下方,那么记作 Ω ( g ( n ) ) \Omega(g(n)) Ω(g(n))
渐进紧界
渐进紧界(asymptotic tight bounds):从某个常数 n 0 n_0 n0开始, f ( n ) f(n) f(n) 总是在 c 1 ∗ g ( n ) c_1*g(n) c1∗g(n) 和 c 2 ∗ g ( n ) c_2*g(n) c2∗g(n) 之间,那么记作 Θ ( g ( n ) ) \Theta(g(n)) Θ(g(n))
2)空间复杂度
与时间复杂度类似,一般也使用大 O O O 表示法来衡量:一个算法执行随数据规模增大,而增长的额外空间成本
public static int binarySearchBasic(int[] a, int target) {
int i = 0, j = a.length - 1; // 设置指针和初值
while (i <= j) { // i~j 范围内有东西
int m = (i + j) >>> 1;
if(target < a[m]) { // 目标在左边
j = m - 1;
} else if (a[m] < target) { // 目标在右边
i = m + 1;
} else { // 找到了
return m;
}
}
return -1;
}
二分查找性能
下面分析二分查找算法的性能
时间复杂度
- 最坏情况: O ( log n ) O(\log n) O(logn)
- 最好情况:如果待查找元素恰好在数组中央,只需要循环一次 O ( 1 ) O(1) O(1)
空间复杂度
- 需要常数个指针 i , j , m i,j,m i,j,m,因此额外占用的空间是 O ( 1 ) O(1) O(1)
3) 递归时间复杂度计算
若有递归式
T
(
n
)
=
a
T
(
n
b
)
+
f
(
n
)
T(n) = aT(\frac{n}{b}) + f(n)
T(n)=aT(bn)+f(n)
其中
- T ( n ) T(n) T(n) 是问题的运行时间, n n n 是数据规模
- a a a 是子问题个数
- T ( n b ) T(\frac{n}{b}) T(bn) 是子问题运行时间,每个子问题被拆成原问题数据规模的 n b \frac{n}{b} bn
- f ( n ) f(n) f(n) 是除递归外执行的计算
令 x = log b a x = \log_{b}{a} x=logba,即 x = log 子问题缩小倍数 子问题个数 x = \log_{子问题缩小倍数}{子问题个数} x=log子问题缩小倍数子问题个数
那么
T
(
n
)
=
{
Θ
(
n
x
)
f
(
n
)
=
O
(
n
c
)
并且
c
<
x
Θ
(
n
x
log
n
)
f
(
n
)
=
Θ
(
n
x
)
Θ
(
n
c
)
f
(
n
)
=
Ω
(
n
c
)
并且
c
>
x
T(n) = \begin{cases} \Theta(n^x) & f(n) = O(n^c) 并且 c \lt x\\ \Theta(n^x\log{n}) & f(n) = \Theta(n^x)\\ \Theta(n^c) & f(n) = \Omega(n^c) 并且 c \gt x \end{cases}
T(n)=⎩
⎨
⎧Θ(nx)Θ(nxlogn)Θ(nc)f(n)=O(nc)并且c<xf(n)=Θ(nx)f(n)=Ω(nc)并且c>x
例1
T ( n ) = 2 T ( n 2 ) + n 4 T(n) = 2T(\frac{n}{2}) + n^4 T(n)=2T(2n)+n4
- 此时 x = 1 < 4 x = 1 < 4 x=1<4,由后者决定整个时间复杂度 Θ ( n 4 ) \Theta(n^4) Θ(n4)
- 如果觉得对数不好算,可以换为求【 b b b 的几次方能等于 a a a】
例2
T ( n ) = T ( 7 n 10 ) + n T(n) = T(\frac{7n}{10}) + n T(n)=T(107n)+n
- a = 1 , b = 10 7 , x = 0 , c = 1 a=1, b=\frac{10}{7}, x=0, c=1 a=1,b=710,x=0,c=1
- 此时 x = 0 < 1 x = 0 < 1 x=0<1,由后者决定整个时间复杂度 Θ ( n ) \Theta(n) Θ(n)
例3
T ( n ) = 16 T ( n 4 ) + n 2 T(n) = 16T(\frac{n}{4}) + n^2 T(n)=16T(4n)+n2
- a = 16 , b = 4 , x = 2 , c = 2 a=16, b=4, x=2, c=2 a=16,b=4,x=2,c=2
- 此时 x = 2 = c x=2 = c x=2=c,时间复杂度 Θ ( n 2 log n ) \Theta(n^2 \log{n}) Θ(n2logn)
例4
T ( n ) = 7 T ( n 3 ) + n 2 T(n)=7T(\frac{n}{3}) + n^2 T(n)=7T(3n)+n2
- a = 7 , b = 3 , x = 1. ? , c = 2 a=7, b=3, x=1.?, c=2 a=7,b=3,x=1.?,c=2
- 此时 x = log 3 7 < 2 x = \log_{3}{7} < 2 x=log37<2,由后者决定整个时间复杂度 Θ ( n 2 ) \Theta(n^2) Θ(n2)
例5
T ( n ) = 7 T ( n 2 ) + n 2 T(n) = 7T(\frac{n}{2}) + n^2 T(n)=7T(2n)+n2
- a = 7 , b = 2 , x = 2. ? , c = 2 a=7, b=2, x=2.?, c=2 a=7,b=2,x=2.?,c=2
- 此时 x = l o g 2 7 > 2 x = log_2{7} > 2 x=log27>2,由前者决定整个时间复杂度 Θ ( n log 2 7 ) \Theta(n^{\log_2{7}}) Θ(nlog27)
例6
T ( n ) = 2 T ( n 4 ) + n T(n) = 2T(\frac{n}{4}) + \sqrt{n} T(n)=2T(4n)+n
- a = 2 , b = 4 , x = 0.5 , c = 0.5 a=2, b=4, x = 0.5, c=0.5 a=2,b=4,x=0.5,c=0.5
- 此时 x = 0.5 = c x = 0.5 = c x=0.5=c,时间复杂度 Θ ( n log n ) \Theta(\sqrt{n}\ \log{n}) Θ(n logn)