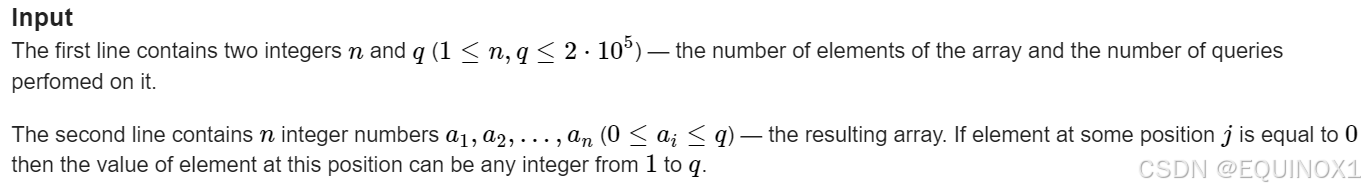一、题目

1、题目描述

2、输入输出

2.1输入

2.2输出

3、原题链接

1023D - Array Restoration

二、解题报告

1、思路分析

先考虑合法性检查：

对于数字x，其最左位置和最右位置 之间如果存在数字比x小，则非法

由于q次操作，第q次操作是最后一次操作，所以数组中应该有q，即没q非法

这个合法性检查是很简单的，我们可以线段树，树状数组，分块，set……

考虑如何构造？

对于每个0，如果处于若干个数字的区间内，那么我们应该填的数字不能比这些区间中最大那个小

同时如果数组没有q，我们优先填q

算法流程：

预处理数组最大值ma，每个数字最左下标L[],最右下标R[]

遍历数组，用一个有序集合st来维护当前遇到的区间左端点

遇到0：

如果ma < q，那么我们填q，ma = q

否则，如果st非空，填st中最大那个

否则，填1

非0：

如果i == L[a[i]]，a[i] 入st

如果 i == R[i], a[i] 出st

如果a[i] < min(st)，非法输出NO

2、复杂度

时间复杂度： O(NlogN)空间复杂度：O(N)

3、代码详解

 ​

#include <bits/stdc++.h>
#define sc scanf
using i64 = long long;
using i128 = __int128;
using PII = std::pair<int, int>;
constexpr int inf32 = 1e9 + 7;
constexpr i64 inf64 = 1e18 + 7;
constexpr int P = 998244353;
constexpr double eps = 1e-6;

// #define DEBUG

void solve()
{
    int n, q;
    std::cin >> n >> q;
    std::vector<int> a(n), L(q + 1, -1), R(q + 1, -1);
    int ma = -1, mi = inf32;

    for (int i = 0; i < n; ++ i) {
        std::cin >> a[i], ma = std::max(ma, a[i]), mi = std::min(mi, a[i]);
        if (L[a[i]] == -1) L[a[i]] = i;
        R[a[i]] = i;
    }

    std::set<int> st;
    for (int i = 0; i < n; ++ i) {
        if (!a[i]) {
            if (ma < q)
                a[i] = q, ma = q;
            else if(st.size())
                a[i] = *std::prev(st.end());
            else
                a[i] = 1;
        }
        else {
            if (L[a[i]] == i && i < R[a[i]]) st.insert(a[i]);
            if (R[a[i]] == i && L[a[i]] < i) st.erase(a[i]);
            if (st.size() && a[i] < *std::prev(st.end())) {
                std::cout << "NO\n";
                return;
            }    
        }
    }
    if (ma < q) {
        std::cout << "NO\n";
        return;    
    }
    std::cout << "YES\n";
    for (int x : a)
        std::cout << x << ' ';

}

int main()
{
#ifdef DEBUG
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
    std::ios::sync_with_stdio(false), std::cin.tie(nullptr), std::cout.tie(nullptr);
    int _ = 1;
    // std::cin >> _;
    while (_--)
        solve();
    return 0;
}