本文章来源于对李沐动手深度学习代码以及原理的理解,并且由于李沐老师的代码能力很强,以及视频中讲解代码的部分较少,所以这里将代码进行尽量逐行详细解释
并且由于pytorch的语法有些小伙伴可能并不熟悉,所以我们会采用逐行解释+小实验的方式来给大家解释代码
在这一块,李沐老师的代码里面其实有很多的测试例子,而这些测试例子往往是劝退初学者的一个很大的因素,为了快速理解并且上手卷积神经网络,我并不会很强调所有的例子,而是根据李沐老师的顺序,将主要框架进行搭建,重要的小例子我会带大家进行浮现,但是具体的一些小例子就让大家自己去试试
本文的动图来自:https://blog.csdn.net/Together_CZ/article/details/115494176
以及一些网络的资料
卷积
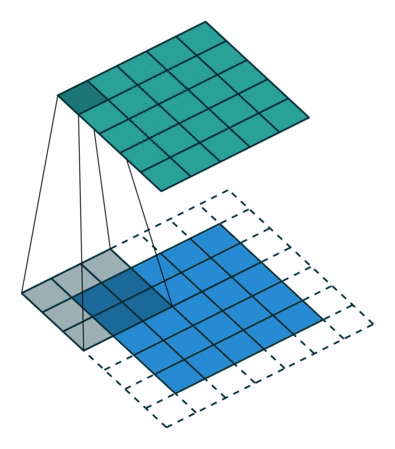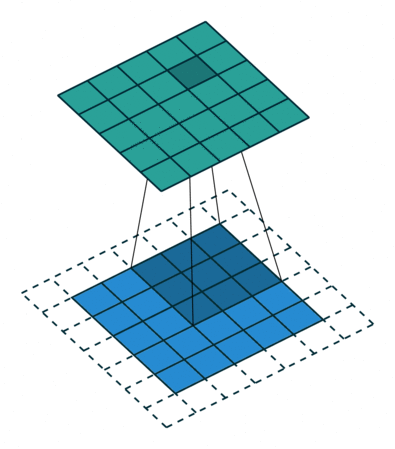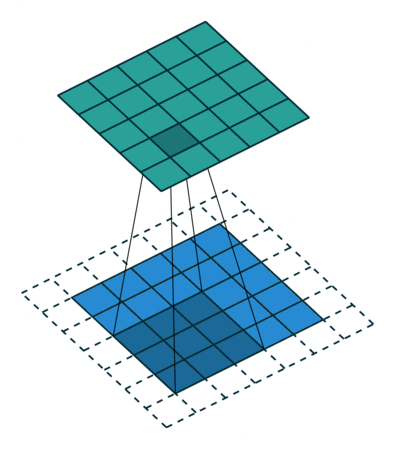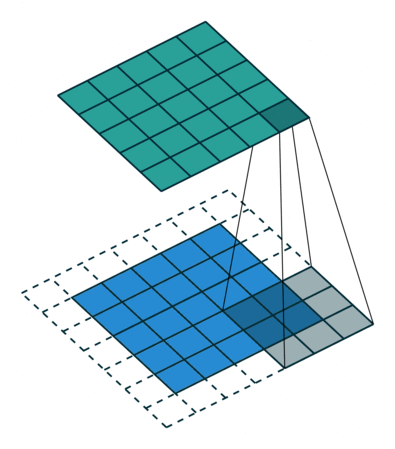
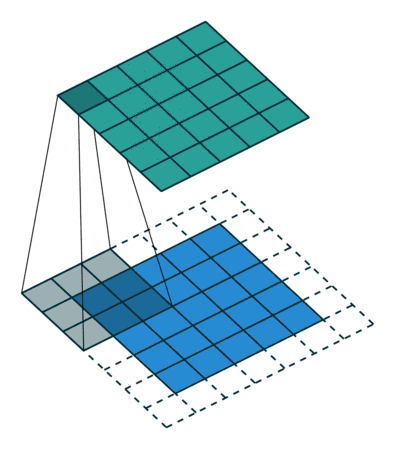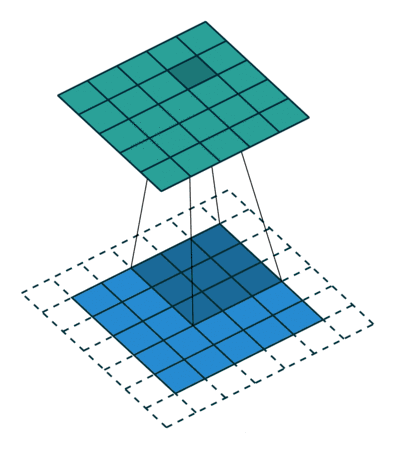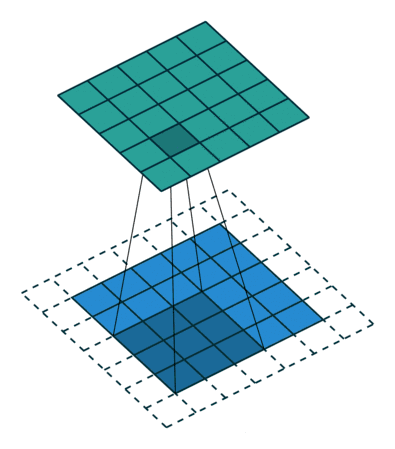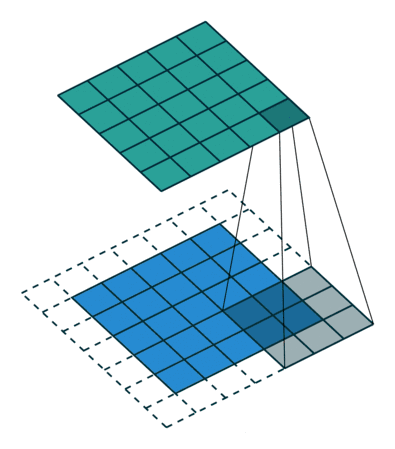
相信工科专业的同学对这个词应该不会陌生,尤其是通信专业,我们经常会做信号卷积的操作,但是在其他的使用上面,我们常常使用的是一维卷积,但是在卷积神经网络中,我们用到的是二维卷积,我们可以用下面这张动图来描述二维卷积:
import torch
from torch import nn
from d2l import torch as d2l
def corr2d(X,K):
# 计算二维互相关运算
h,w = K.shape # 核矩阵的行数和列数
Y = torch.zeros((X.shape[0]-h+1,X.shape[1]-w+1)) # 输出的高度和宽度
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i,j] = (X[i:i+h,j:j+w]*K).sum()
return Y
我们使用这一段代码来描述这样的一个卷积的过程,这个代码实际上没有很大的难度,但是我们需要弄清楚的是卷积前和卷积后,二维图像尺寸的变化
我认为大家只需要记住一个公式,就可以弄清楚卷积和其他操作之后,我们图像的尺寸了(这里默认二维图像的高和宽是一样的,这里算出的是边长):
O
u
p
u
t
=
(
I
n
p
u
t
+
2
∗
p
a
d
d
i
n
g
−
k
e
r
n
e
l
)
/
s
t
r
i
d
e
+
1
结果向下取整
Ouput = (Input+2*padding-kernel)/stride+1\\结果向下取整
Ouput=(Input+2∗padding−kernel)/stride+1结果向下取整
这个公式的具体推导我们可以看Pytorch官网的推导,这里我也可以把链接放在这里尺寸公式推导
或许初学者小伙伴们就会有疑惑,Output和Input我们都知道,是输入和输出;但是padding,kernel,stride是什么呢?没关系,我们后面会进行解释
卷积层
在上面的代码里面,我们已经实现了一个卷积操作,卷积层实际上就是将这个卷积操作做成一个类
# 实现二维卷积层
class Conv2d(nn.Module):
def __init__(self,kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(nn.zeros(1))
def forward(self,x):
return corr2d(x,self.weight)+self.bias
如果对类这个概念不是特别了解的同学,可以去看看我之前的文章,有讲解python的类的文章
需要注意的是,由于我们继承了父类nn.Module,所以__call__方法在这里写成forward方法,两者是等价的,我们先来讲解一下卷积层比较重要的一个参数kernel_size
Kernel_size
这个参数表示卷积核的大小,我们根据上面的动图来看,卷积核的大小是3×3,因为映射到图片上的影子是3×3的
或许你会认为这样的实现方式过于麻烦,我们当然也有更简单的实现方法,就是调用torch.nn模型中的Conv2d的函数,我们下面就对这个重要的函数进行讲解
torch.nn.Conv2d
conv2d = nn.Conv2d(1,1,kernel_size=(1,2),bias=False)
这个函数大家其实很好理解,实际上就是创建一个卷积层,但是可能会让大家疑惑的是,这个函数的一些参数是怎么样的
我们可以找到pytorch官网的参数:
nn.Conv2d(in_channels,out_channels,kernel_size,stride,padding)
我们来一个个参数的理解:
①in_channels这个参数代表输入的通道数,通道这个概念我们后面会进行讲解
②out_channels这个参数代表输出的通道数
③kernel_size这个参数表示卷积核的大小
④stride这个参数表示步幅,表示我们每一次卷积挪动的大小
⑤padding这个参数表示扩张,padding为原来图像加宽的程度
stride和padding这两个参数比较简单,我们可以用两个图来描述:
padding
这个动图的虚线部分也就是padding
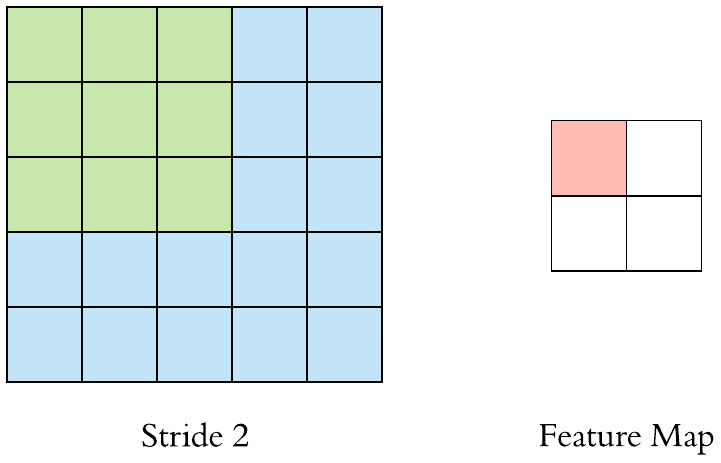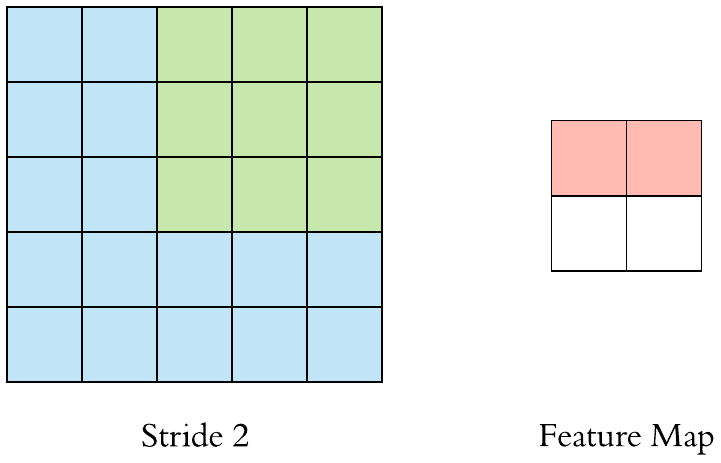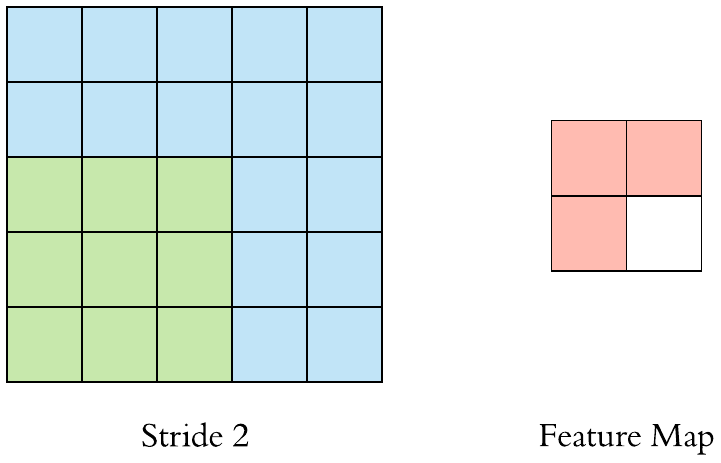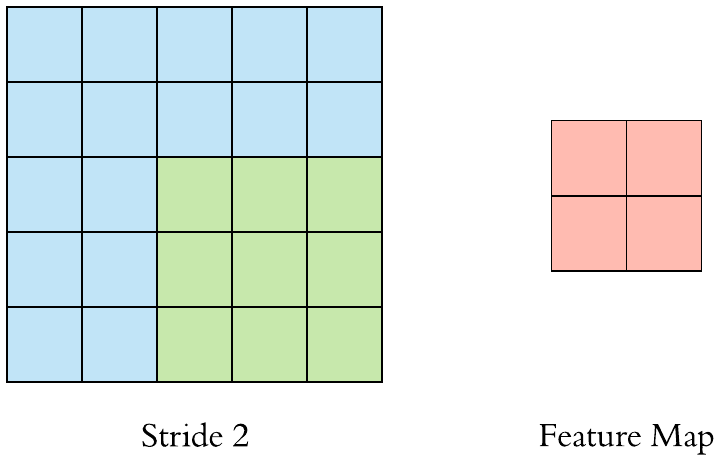
stride
小实验
我们这个小实验就根据我们上面讲的输入输出的尺寸公式以及刚刚讲的函数,对我们的公式进行一个验证:
x = torch.rand(1,2,8,8)
conv2d = nn.Conv2d(2,1,kernel_size=3,padding=1,stride=2)
y = conv2d(x)
print(x.shape)
print(y.shape)
>>> torch.Size([1, 2, 8, 8])
>>> torch.Size([1, 1, 4, 4])
我们先来逐行理解一下我的这个代码
x = torch.rand(1,2,8,8)这个代码表示我们初始化一个尺寸为(1,2,8,8)的一个tensor数据类型,大家可能对这个有一些不解
我们一般交给卷积层处理的数据需要有四个维度,分别是[N,C,H,W],也即是**[批量大小,通道数,高,宽]**
我们在代码中写到
nn.Conv2d(2,1,kernel_size=3,padding=1,stride=2),我们指定输入通道数目为2,输出通道数目为1,结果也很好的显示了我们确实成功的把通道数从2改成了1
接着我们进行运算,套用上面的尺寸变化公式:
o
u
t
p
u
t
=
(
8
−
3
+
2
×
1
)
/
2
+
1
=
4.5
output = (8-3+2×1)/2+1=4.5
output=(8−3+2×1)/2+1=4.5
向下取整之后得到4,说明我们的公式讲解是正确的
卷积层梯度下降
# 学习由X生成Y的卷积核
conv2d = nn.Conv2d(1,1,kernel_size=(1,2),bias=False)
X = X.reshape((1,1,6,8))
Y = Y.reshape((1,1,6,7))
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat-Y)**2
conv2d.zero_grad()
l.sum().backward()
conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad # 实际上是在做一个梯度下降,学习率是3e-2
if (i+1)%2 == 0:
print(f'batch{i+1},loss{l.sum():.3f}')
在这个代码里面,我们还是仿照前面的梯度下降,设置了损失函数为L,然后设置学习率为3e-2,最后得到结果为
batch2,loss10.328
batch4,loss2.925
batch6,loss0.979
batch8,loss0.364
batch10,loss0.143
池化层
卷积操作对位置是非常的敏感的,所以我们需要一定的平移不变性,实际中会有很多因素导致图像有细微的区别,所以对位置太敏感并不是一件特别好的事情,池化层可以类似于一种激活函数
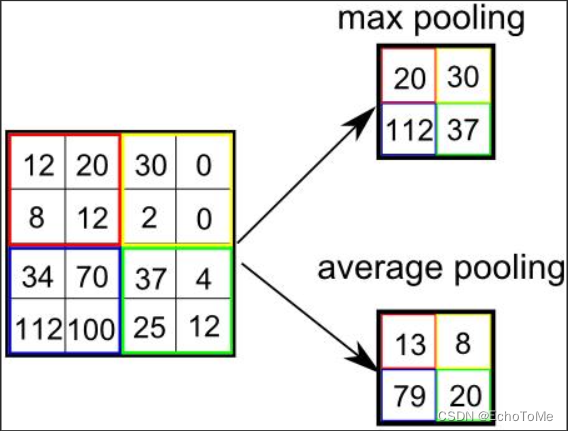
我们一般常用的是二维最大池化和二维平均池化
这个图很好的讲解了池化操作是怎么样子的
我们下面来区分一下最大池化和平均池化
最大池化层:每个窗口中最强的模式信号
平均池化层:每个窗口中平均的模式信号
def pool2d(X,pool_size,mode='max'):
p_h,p_w = pool_size
Y = torch.zeros((X.shape[0]-p_h+1,X.shape[1]-p_w+1)) # 输出维度
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i,j] = X[i:i+p_h,j:j+p_w].max()
elif mode == 'avg':
Y[i,j] = X[i:i+p_h,j:j+p_w].mean()
return Y
这个池化的代码比较好理解,就是将卷积的累加变成找最大值和找平均值
小实验
我们可以来验证一下池化层的输入和输出,并且池化层可以看作是特殊的卷积层,所以它也满足输入输出的尺寸变化*
X = torch.tensor([[0.0,1.0,2.0],[3.0,4.0,5.0],[6.0,7.0,8.0]])
X
>>>tensor([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]])
接下来我们来通过一个池化层看看结果:
pool2d(X,(2,2),mode='avg')
>>>tensor([[2., 3.],
[5., 6.]])
池化层
在这里我们就不像卷积层一样从0开始实现了,我们直接调用torch.nn的函数即可
X = torch.arange(16,dtype=torch.float32).reshape((1,1,4,4))
pool2d = nn.MaxPool2d(3)
>>> tensor([[[[10.]]]])
这里我们需要注意的是,当最大池化层不规定步幅的时候,步幅默认和池化核尺寸一样
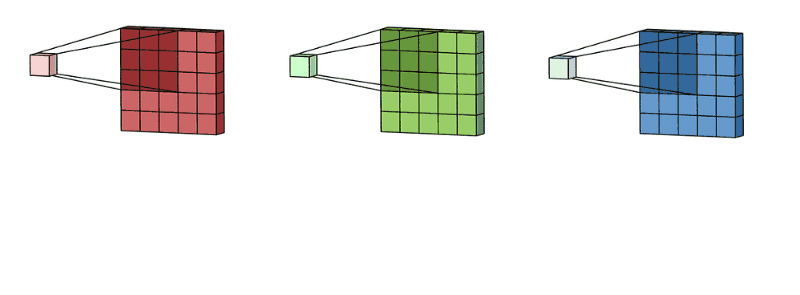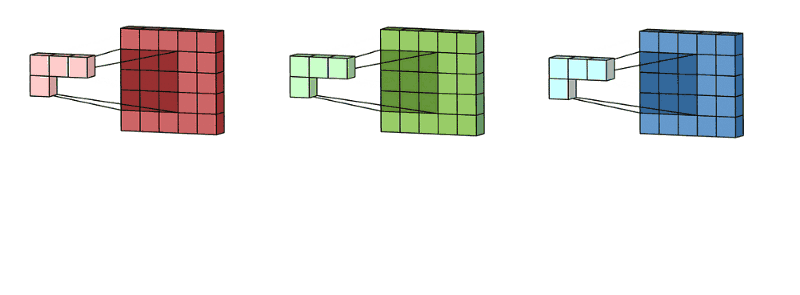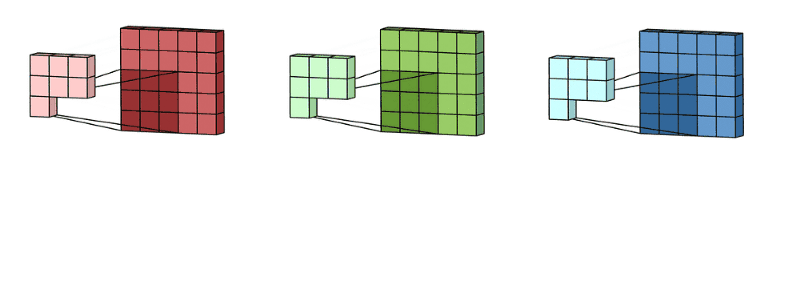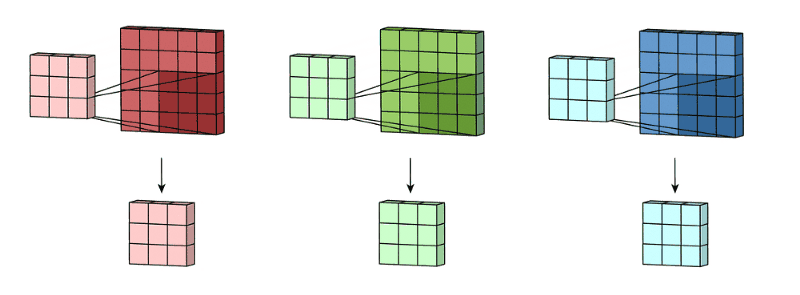
多输入多输出通道
多输入通道
通过这两个动图
import torch
from d2l import torch as d2l
# 多输入的计算函数
def corr2d_multi_in(X,K):
return sum(d2l.corr2d(x,k) for x,k in zip(X,K))
上面的这个函数就是计算多输入通道的函数,我们下面跟着李沐老师的思路来测试一下
X=torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K=torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
corr2d_multi_in(X, K)
>>> tensor([[ 56., 72.],
[104., 120.]])
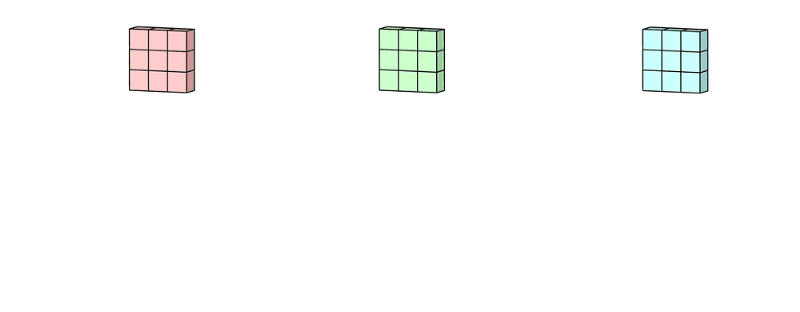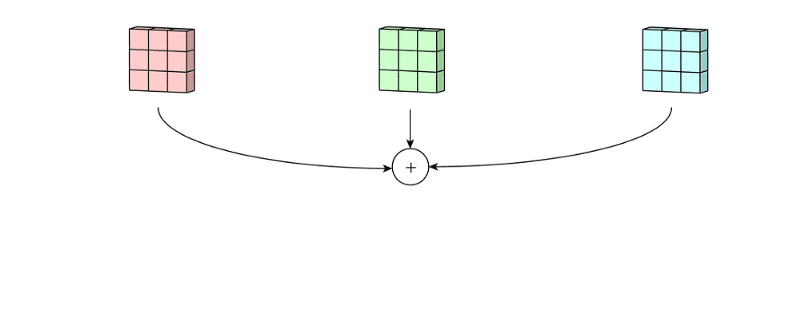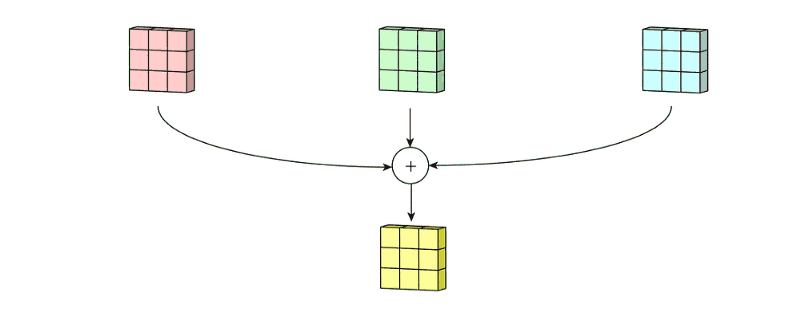
我们从代码看出来,这里的输入X有两个通道,相应的,也会有两个对应的卷积核,下面我们来复刻一下上面的动图:
小实验
from torch import nn
A = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K1 = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
B = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]])
K2 = torch.tensor([[1.0, 2.0], [3.0, 4.0]])
这里我们将两个通道进行拆开,分为A和B两个,将两个通道的卷积核也进行分开,分为K1和K2
Y1 = d2l.corr2d(A,K1)
Y1
>>> tensor([[19., 25.],
[37., 43.]])
Y2 = d2l.corr2d(B,K2)
Y2
>>> tensor([[37., 47.],
[67., 77.]])
Y1+Y2
>>> tensor([[ 56., 72.],
[104., 120.]])
我们可以看出来,这个Y1+Y2和之前的结果是一样的,所以我们成功的验证了多通道卷积的过程
多输出通道
# 多输出通道的计算函数
def corr2d_multi_in_out(X,K):
return torch.stack([corr2d_multi_in(X,K) for k in K],0)
K=torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
K = torch.stack((K,K+1,K+2),0)
K.shape
>>> torch.Size([3, 2, 2, 2])
我们这里生成的K是一个批量大小为3,通道数目为2的一个tensor的数据类型
X=torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K=torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
corr2d_multi_in_out(X,K)
>>> tensor([[[ 56., 72.],
[104., 120.]],
[[ 56., 72.],
[104., 120.]]])
可能到这里,很多小伙伴就看不懂了,但是不要怕,我们慢慢的对代码进行拆开讲解:
小实验
for k in K:
print(corr2d_multi_in(X,K))
>>> tensor([[ 56., 72.],
[104., 120.]])
tensor([[ 56., 72.],
[104., 120.]])
根据这个代码,我们可以知道,我们输出的通道是根据卷积核的个数来判断的,也就是我们输出的通道数目和我们给定卷积核的个数是一样的
为了验证我们的想法,可以再来试试:
K=torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]],[[2.0,3.0],[4.0,5.0]]])
tmp = torch.stack([corr2d_multi_in(X,K) for k in K],0)
tmp
>>> tensor([[[ 56., 72.],
[104., 120.]],
[[ 56., 72.],
[104., 120.]],
[[ 56., 72.],
[104., 120.]]])