✨:2022 CSP-J 第二轮认证真题解析
💟:幸愉编程
💜: 学习如逆水行舟,不进则退 💜💜
🌸: 如有错误或不足之处,希望可以指正,非常感谢😉
2022 CSP-J 第二轮认证真题解析💭💭
[CSP-J 2022] T1 乘方
题目描述
小文同学刚刚接触了信息学竞赛,有一天她遇到了这样一个题:给定正整数 a a a 和 b b b,求 a b a^b ab 的值是多少。
a b a^b ab 即 b b b 个 a a a 相乘的值,例如 2 3 2^3 23 即为 3 3 3 个 2 2 2 相乘,结果为 2 × 2 × 2 2 \times 2 \times2 2×2×2 = 8 8 8。
“简单!”小文心想,同时很快就写出了一份程序,可是测试时却出现了错误。
小文很快意识到,她的程序里的变量都是 int 类型的。在大多数机器上, i n t int int 类型能表示的最大数为 2 31 2^{31} 231 - 1 1 1 ,因此只要计算结果超过这个数,她的程序就会出现错误。
由于小文刚刚学会编程,她担心使用 i n t int int 计算会出现问题。因此她希望你在 a b a^b ab 的值超过 10 9 {10}^9 109 时,输出一个 − 1 -1 −1 进行警示,否则就输出正确的 a b a^b ab 的值。
然而小文还是不知道怎么实现这份程序,因此她想请你帮忙。
输入格式
输入共一行,两个正整数 a a a, b b b。
输出格式
输出共一行,如果 a b a^b ab 的值不超过 10 9 {10}^9 109,则输出 a b a^b ab 的值,否则输出 − 1 -1 −1。
样例
输入样例1
10 9
输出样例1
1000000000
输入样例2
23333 66666
输出样例2
-1
提示/说明
对于
10
%
10 \%
10% 的数据,保证
b
=
1
b = 1
b=1。
对于
30
%
30 \%
30% 的数据,保证
b
≤
2
b \le 2
b≤2。
对于
60
%
60 \%
60% 的数据,保证
b
≤
30
b
b \le 30b
b≤30b,
a
b
≤
10
18
a^b \le {10}^{18}
ab≤1018
对于
100
%
100 \%
100% 的数据,保证
1
≤
a
,
b
≤
10
9
1 \le a, b \le {10}^9
1≤a,b≤109
解析
思路
判断一下 a 2 a^2 a2 的最小值大于 1 0 9 10^9 109,化解出 a大于等于31700时最后的结果一定大于 1 0 9 10^9 109,然后写个快速幂求 a b a^b ab,特判结果是否可能大于 1 0 9 10^9 109,大于 1 0 9 10^9 109 返回 -1,否则返回结果,骗分大法是直接读取后输出 -1 可以拿 25 % 25\% 25% 的分数,简单送分题。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL quick_pow(LL a, LL b){
if(b>=2 && a >= 31700) return -1;
LL res = 1;
while(b > 0){
if(b&1) res *= a;
a = a*a;
b >>= 1;
if(res > 1e9) return -1;
}
return res;
}
int main()
{
int a, b;
cin>>a>>b;
cout<<quick_pow(a, b);
return 0;
}
[CSP-J 2022] T2 解密
题目描述
给定一个正整数 k k k,有 k k k 次询问,每次给定三个正整数 n i n_i ni, e i e_i ei, d i d_i di,求两个正整数 p i p_i pi, q i q_i qi,使 n i = p i × q i n_i = p_i \times q_i ni=pi×qi 、 e i × d i = ( p i − 1 ) ( q i − 1 ) + 1 e_i \times d_i = (p_i - 1)(q_i - 1) + 1 ei×di=(pi−1)(qi−1)+1。
输入格式
第一行一个正整数
k
k
k,表示有
k
k
k 次询问。
接下来
k
k
k 行,第
i
i
i 行三个正整数
n
i
n_i
ni,
d
i
d_i
di,
e
i
e_i
ei 。
输出格式
输出
k
k
k 行,每行两个正整数
p
i
,
q
i
p_i, q_i
pi,qi 表示答案。
为使输出统一,你应当保证
p
i
≤
q
i
p_i \leq q_i
pi≤qi。
如果无解,请输出
N
O
NO
NO。
输入样例
10
770 77 5
633 1 211
545 1 499
683 3 227
858 3 257
723 37 13
572 26 11
867 17 17
829 3 263
528 4 109
输出样例
2 385
NO
NO
NO
11 78
3 241
2 286
NO
NO
6 88
提示/说明
【数据范围】
以下记
m
=
n
−
e
×
d
+
2
m = n - e \times d + 2
m=n−e×d+2。
保证对于
100
%
100\%
100% 的数据,
1
≤
k
≤
10
5
1 \leq k \leq {10}^5
1≤k≤105 ,对于任意的
1
≤
i
≤
k
1 \leq i \leq k
1≤i≤k,
1
≤
n
i
≤
10
18
1 \leq n_i \leq {10}^{18}
1≤ni≤1018 ,
1
≤
e
i
×
d
i
≤
10
18
1 \leq e_i \times d_i \leq {10}^{18}
1≤ei×di≤1018,
1
≤
m
≤
10
9
1 \leq m \leq {10}^9
1≤m≤109 。
| 测试点编号 | k ≤ k≤ k≤ | n ≤ n≤ n≤ | m ≤ m≤ m≤ | 特殊性质 |
|---|---|---|---|---|
| 1 1 1 | 1 0 3 10^3 103 | 1 0 3 10^3 103 | 1 0 3 10^3 103 | 保证有解 |
| 2 2 2 | 1 0 3 10^3 103 | 1 0 3 10^3 103 | 1 0 3 10^3 103 | 无 |
| 3 3 3 | 1 0 3 10^3 103 | 1 0 9 10^9 109 | 6 × 1 0 4 6\times10^4 6×104 | 保证有解 |
| 4 4 4 | 1 0 3 10^3 103 | 1 0 9 10^9 109 | 6 × 1 0 4 6\times10^4 6×104 | 无 |
| 5 5 5 | 1 0 3 10^3 103 | 1 0 9 10^9 109 | 1 0 9 10^9 109 | 保证有解 |
| 6 6 6 | 1 0 3 10^3 103 | 1 0 9 10^9 109 | 1 0 9 10^9 109 | 无 |
| 7 7 7 | 1 0 5 10^5 105 | 1 0 18 10^{18} 1018 | 1 0 9 10^9 109 | 保证若有解则 p = q p=q p=q |
| 8 8 8 | 1 0 5 10^5 105 | 1 0 18 10^{18} 1018 | 1 0 9 10^9 109 | 保证若有解 |
| 9 9 9 | 1 0 5 10^5 105 | 1 0 18 10^{18} 1018 | 1 0 9 10^9 109 | 无 |
| 10 10 10 | 1 0 5 10^5 105 | 1 0 18 10^{18} 1018 | 1 0 9 10^9 109 | 无 |
解析
解题思路
∵
e
d
=
(
p
−
1
)
(
q
−
1
)
+
1
ed = (p - 1)(q - 1) + 1
ed=(p−1)(q−1)+1
∴
e
d
=
p
q
−
p
−
q
+
2
ed = pq - p - q + 2
ed=pq−p−q+2
∵
p
q
=
n
pq = n
pq=n
∴
e
d
=
n
−
p
−
q
+
2
ed = n - p - q + 2
ed=n−p−q+2
p
+
q
=
n
−
e
d
+
2
p + q = n - ed + 2
p+q=n−ed+2 (
n
n
n、
e
e
e、
d
d
d 是已知量)
n
−
e
d
+
2
n - ed + 2
n−ed+2 则可以求出,令其为
k
k
k
将
p
=
k
−
q
p = k - q
p=k−q (
p
≤
q
p ≤ q
p≤q) 代入
p
q
=
n
pq = n
pq=n
(
k
−
q
)
q
=
n
k-q)q = n
k−q)q=n ==>
−
q
2
+
k
q
−
n
=
0
-q^2 + kq - n = 0
−q2+kq−n=0
一元二次方程求根公式:形如 a x 2 + b x + c = 0 ax^2 + bx + c = 0 ax2+bx+c=0
x = ( − b ± √ b 2 − 4 a c ) x = (-b ± √b^2 - 4ac) x=(−b±√b2−4ac)
q
2
−
k
q
+
n
=
0
=
=
>
x
=
(
−
k
±
√
k
2
−
4
n
)
q^2 - kq + n = 0 ==> x = (-k ±√k^2 - 4n)
q2−kq+n=0==>x=(−k±√k2−4n)
题目要求
p
p
p、
q
q
q 是正整数,所以
Δ
<
0
Δ < 0
Δ<0 或者
√
Δ
∉
Z
√Δ∉Z
√Δ∈/Z 无解,否则输出
p
p
p 和
q
q
q 的值。
数学代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n, k, e, d, m, p, q;
int main () {
cin >> k;
while (k-- ){
cin >> n >> d >> e;
m = n - e * d + 2;
LL tmp = m*m - 4*n;
if(tmp < 0 || (LL)sqrt(tmp)*(LL)sqrt(tmp) != tmp){
cout<<"NO"<<endl;
continue;
}
tmp = (LL)sqrt(tmp);
cout << (m-tmp)/2 << ' ' << (m+tmp)/2 <<endl;
}
return 0;
}
二分代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n, k, e, d;
int main () {
cin >> k;
while (k -- ) {
cin >> n >> d >> e;
LL k = n - e * d + 2;
LL l = 1, r = k, p, q;
while (l < r) {
p = (l + r) / 2;
q = k - p;
if (n == p * q) break;
else if (n <= p * q) r = p;
else l = p + 1;
}
if (n == p * q){
if(p <= q)
cout << p << ' ' << q << endl;
else
cout<< q << ' ' << p << endl;
}
else cout << "NO" << endl;
}
return 0;
}
[CSP-J 2022] T3 逻辑表达式
题目描述
逻辑表达式是计算机科学中的重要概念和工具,包含逻辑值、逻辑运算、逻辑运算优先级等内容。
在一个逻辑表达式中,元素的值只有两种可能:
0
0
0(表示假)和
1
1
1(表示真)。元素之间有多种可能的逻辑运算,本题中只需考虑如下两种:“与”(符号为 &)和“或”(符号为 |)。其运算规则如下:
0
&
0
=
0
&
1
=
1
&
0
=
0
0 \mathbin{\&} 0 = 0 \mathbin{\&} 1 = 1 \mathbin{\&} 0 = 0
0&0=0&1=1&0=0。,
1
&
1
=
1
1 \mathbin{\&} 1 = 1
1&1=1;
0
∣
0
=
0
,
0
∣
1
=
1
∣
0
=
1
∣
1
=
1
0 \mathbin{|} 0 =0,0 \mathbin{|} 1 = 1 \mathbin{|} 0 = 1 \mathbin{|}1 = 1
0∣0=0,0∣1=1∣0=1∣1=1。
在一个逻辑表达式中还可能有括号。规定在运算时,括号内的部分先运算;两种运算并列时,& 运算优先于 | 运算;同种运算并列时,从左向右运算。
比如,表达式 0|1&0 的运算顺序等同于 0|(1&0);表达式 0&1&0|1 的运算顺序等同于 ((0&1)&0)|1。
此外,在 C++ 等语言的有些编译器中,对逻辑表达式的计算会采用一种“短路”的策略:在形如 a&b 的逻辑表达式中,会先计算
a
a
a 部分的值,如果
a
=
0
a = 0
a=0,那么整个逻辑表达式的值就一定为
0
0
0,故无需再计算
b
b
b 部分的值;同理,在形如 a|b 的逻辑表达式中,会先计算
a
a
a 部分的值,如果
a
=
1
a = 1
a=1,那么整个逻辑表达式的值就一定为
1
1
1,无需再计算
b
b
b 部分的值。
现在给你一个逻辑表达式,你需要计算出它的值,并且统计出在计算过程中,两种类型的“短路”各出现了多少次。需要注意的是,如果某处“短路”包含在更外层被“短路”的部分内则不被统计,如表达式 1|(0&1) 中,尽管 0&1 是一处“短路”,但由于外层的 1|(0&1) 本身就是一处“短路”,无需再计算 0&1 部分的值,因此不应当把这里的 0&1 计入一处“短路”。
输入格式
输入共一行,一个非空字符串 s s s 表示待计算的逻辑表达式。
输出格式
输出共两行,第一行输出一个字符
0
0
0 或
1
1
1,表示这个逻辑表达式的值;第二行输出两个非负整数,分别表示计算上述逻辑表达式的过程中,形如 a&b 和 a|b 的“短路”各出现了多少次。
样例
输入样例1
0&(1|0)|(1|1|1&0)
输出样例1
1
1 2
输入样例2
(0|1&0|1|1|(1|1))&(0&1&(1|0)|0|1|0)&0
输出样例2
0
2 3
提示/说明
【样例解释 #1】
该逻辑表达式的计算过程如下,每一行的注释表示上一行计算的过程:
0&(1|0)|(1|1|1&0)
=(0&(1|0))|((1|1)|(1&0)) //用括号标明计算顺序
=0|((1|1)|(1&0)) //先计算最左侧的 &,是一次形如 a&b 的“短路”
=0|(1|(1&0)) //再计算中间的 |,是一次形如 a|b 的“短路”
=0|1 //再计算中间的 |,是一次形如 a|b 的“短路”
=1
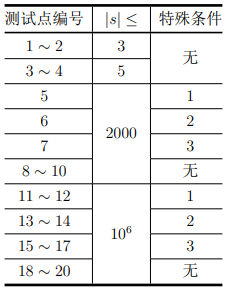
【数据范围】
设
∣
s
∣
|s|
∣s∣ 为字符串
s
s
s 的长度。
对于所有数据, 1 ≤ ∣ s ∣ ≤ 1 0 6 1≤|s|≤10^6 1≤∣s∣≤106。保证 s s s 中仅含有字符 0 0 0、 1 1 1、 & \& &、 ∣ | ∣、 ( ( (、 ) ) ) 且是一个符合规范的逻辑表达式。
保证输入字符串的开头、中间和结尾均无额外的空格。
保证
s
s
s 中没有重复的括号嵌套(即没有形如
(
(
a
)
)
((a))
((a)) 形式的子串,其中
a
a
a 是符合规范的逻辑表达式)。
其中:
特殊性质
1
1
1 为:保证
s
s
s 中没有字符 &。
特殊性质
2
2
2 为:保证
s
s
s 中没有字符 |。
特殊性质
3
3
3 为:保证
s
s
s 中没有字符 ( 和 )。
提示
以下给出一个“符合规范的逻辑表达式”的形式化定义:
字符串
0
0
0 和
1
1
1 是符合规范的;
如果字符串
s
s
s 是符合规范的,且
s
s
s 不是形如
(
t
)
(t)
(t) 的字符串(其中
t
t
t 是符合规范的),那么字符串
(
s
)
(s)
(s) 也是符合规范的;
如果字符串
a
a
a 和
b
b
b 均是符合规范的,那么字符串 a&b、a|b 均是符合规范的;
所有符合规范的逻辑表达式均可由以上方法生成。
解析
思路
中缀表达式转后缀表达式,开个
p
a
i
r
pair
pair 记录 a&b 和 a|b 短路次数即可。
代码
#include <bits/stdc++.h>
#define f first
#define s second
using namespace std;
stack<char> op;
stack<int> num;
stack<pair<int,int>> res;
void work()
{
int a = num.top(); num.pop(); //靠右的数
int b = num.top(); num.pop(); //靠左的数
pair<int,int> c, d;
c = res.top(), res.pop(); // 靠右的数的记录
d = res.top(), res.pop(); // 靠左的数的记录
char x = op.top(); op.pop(); // 操作符号
if(x == '&'){
num.push(a & b);
if(b == 0){ //短路
res.push({d.f + 1, d.s});
}else{
res.push({d.f + c.f, d.s + c.s});
}
}
if(x == '|'){
num.push(a | b);
if(b == 1){
res.push({d.f, d.s + 1});
}else{
res.push({d.f+c.f, d.s + c.s});
}
}
}
int main()
{
unordered_map<int,int>p{{'&', 2}, {'|', 1}}; //设置优先级
string str;
cin>>str;
for(int i = 0; i < str.size(); i++){
auto x = str[i];
if(x >= '0' && x <= '9'){
int y = x - '0';
num.push(y);
res.push({0, 0});
}
else if(x == '(') op.push(x); //左括号
else if(x == ')') //右括号
{
while(op.top() != '('){
work();
}
op.pop();
}
else //运算符
{
while(!op.empty() && p[op.top()] >= p[x]) work();
op.push(x);
}
}
//剩余运算符
while(!op.empty()) work();
printf("%d\n",num.top());
printf("%d %d\n",res.top().f, res.top().s);
return 0;
}
[CSP-J 2022]T4 上升点列
题目描述
在一个二维平面内,给定 n n n 个整数点 ( x i , y i x_i, y_i xi,yi),此外你还可以自由添加 k k k 个整数点。
你在自由添加 k k k 个点后,还需要从 n + k n + k n+k 个点中选出若干个整数点并组成一个序列,使得序列中任意相邻两点间的欧几里得距离恰好为 1 1 1 而且横坐标、纵坐标值均单调不减,即 x i + 1 − x i = 1 , y i + 1 = y i x_{i+1} - x_i = 1, y_{i+1} = y_i xi+1−xi=1,yi+1=yi 或 y i + 1 − y i = 1 y_{i+1} - y_i = 1 yi+1−yi=1, x i + 1 = x i x_{i+1} = x_i xi+1=xi。请给出满足条件的序列的最大长度。
输入格式
第一行两个正整数
n
,
k
n, k
n,k 分别表示给定的整点个数、可自由添加的整点个数。
接下来
n
n
n 行,第
i
i
i 行两个正整数
x
i
,
y
i
x_i, y_i
xi,yi 表示给定的第
i
i
i 个点的横纵坐标。
输出格式
输出一个整数表示满足要求的序列的最大长度。
样例
输入样例1
8 2
3 1
3 2
3 3
3 6
1 2
2 2
5 5
5 3
输出样例1
8
输入样例2
4 100
10 10
15 25
20 20
30 30
输出样例2
103
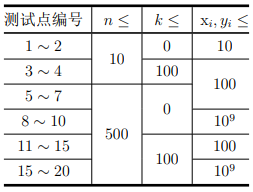
提示/说明
【数据范围】
保证对于所有数据满足:
1
≤
n
≤
500
1 \leq n \leq 500
1≤n≤500,
0
≤
k
≤
100
0 \leq k \leq 100
0≤k≤100。对于所有给定的整点,其横纵坐标
1
≤
x
i
,
y
i
≤
10
9
1 \leq x_i, y_i \leq {10}^9
1≤xi,yi≤109,且保证所有给定的点互不重合。对于自由添加的整点,其横纵坐标不受限制。
解析
思路
floyd 求两点之间最少需要的桥梁个数,distance 函数求第
i
i
i 个点到第 j 个点之间连接起来需要几个桥梁。第
i
i
i 个点到第
j
j
j 个点最少需要的桥梁个数小于等于允许添加的桥梁个数,最后比较更新一下最大值即可。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
int n,k;
int x[501],y[501];
LL d[501][501];
int distance(int i,int j)
{
return abs(x[i]-x[j])+abs(y[i]-y[j]);
}
void floyd() //多源最短路径
{
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
d[i][j] = min(d[i][j], d[i][k]+d[k][j]);
}
int main()
{
cin>>n>>k;
for(int i = 1; i <= n; i++)cin>>x[i]>>y[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++){
if(i != j && x[i] <= x[j] && y[i] <= y[j])
d[i][j] = distance(i, j) - 1;
else d[i][j] = 2147483647;
}
floyd();
LL res = 0;
for(int i = 1;i <= n; i++)
for(int j = 1; j <= n; j++)
if(d[i][j] <= k)
res = max(res, distance(i,j) - d[i][j] + k + 1);
cout<<res;
}
结语
由于忙于考教资和考研的事情,题目一直没有去做,做完后第一题可以使用快速幂快速求,暴力枚举问题也不大;第二题二分或者韦达定理;第三题最难,中缀转后缀表达式;第四题可以套个 floyed 或者使用动态规划解决,参考最长上升子序列,2023祝大家 RP++。