目录
一、欧几里得算法
欧几里得算法又称辗转相除法,可用于求解两个数的最大公约数
其思路:
- gcd(a, b) = gcd(b, a%b),其中gcd(a, b)代表a和b的最大公约数
- 当b=0时,a为最大公约数
例如要求36和24的最大公约数即gcd(36, 24),可转而求gcd(24, 36%24)即gcd(24, 12),再转为求gcd(12, 0),此时最大公约数即为12
其代码实现:
int gcd(int a, int b)
{
if(b == 0)
return a;
return gcd(b, a % b);
}二、拓展欧几里得算法
2.1 裴蜀定理
- 若a,b是整数,且d = gcd(a, b),则对于任意的整数x和y,总有ax+by是d的倍数
- 对于给定的整数x和y,方程ax+by=c有整数解(x, y)的充分必要条件是c是gcd(a, b)的倍数
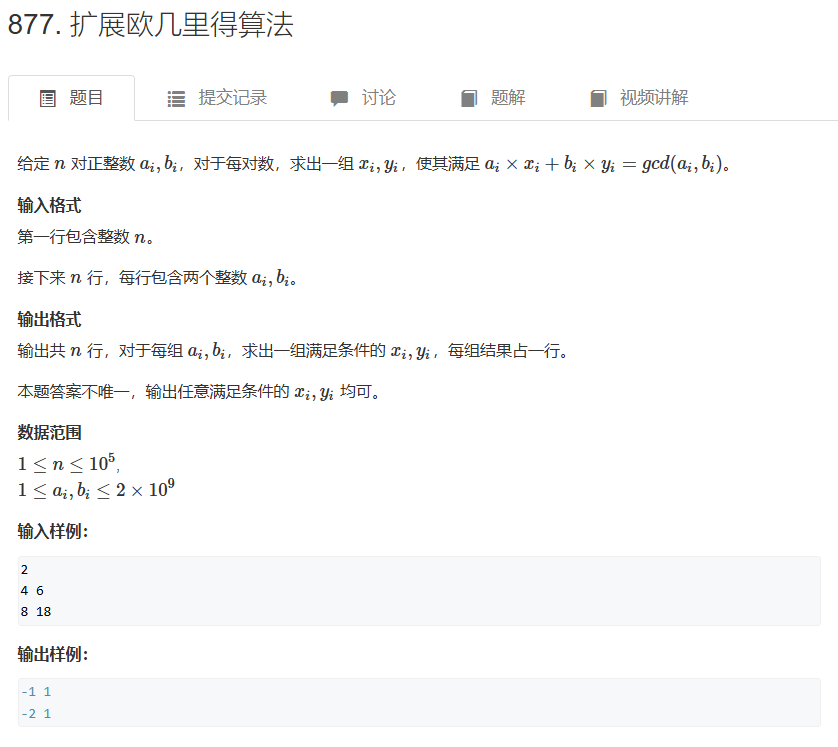
2.2 拓展欧几里得算法
由裴蜀定理,我们知道对于给定的整数a和b,方程ax + by = gcd(a, b)总有整数解(x, y)
那么,如何求出这个整数解(x, y)?
- 由欧几里得算法可得gcd(a, b) = gcd(b, a%b)
- 由裴蜀定理,bx' + (a%b)y' = gcd(b, a%b)
- 由1和2,得bx' + (a%b)y' = gcd(a, b) 即 ax + by = bx' + (a%b)y'
- 由a%b = a - b*(a/b)【注意这里的a/b是向下取整】,得ax + by = bx' + [a - b*(a/b)]y'
- 上式整理得a(x-y') - b[x' - y - (a/b)y'] = 0,即x-y'=0、x' - y - (a/b)y'=0
- 得x = y',y = x'-(a/b)y'
得到求解后,我们就可以通过递归不断传入x和y来计算整数解(x, y)了。拓展欧几里得的递归终点和欧几里得的终点类似,当b为0时即ax+by = a时返回{x=1,y=0}的解,并通过上一次的结果向下更新
拓展欧几里得算法的代码实现:
int exgcd(int a, int b, int &x, int &y) //扩展欧几里得算法
{
if(b == 0) //b为0时结束递归
{
x = 1; //ax+by=a->x=1,y=0
y = 0;
return a;
}
int gcd = exgcd(b, a%b, y, x); //递归求x'和y'
y -= (a/b) * x; //此时递归后x=y',y=x',将y=x'-(a/b)y'转为y=y-(a/b)x得y-=(a/b)x
return gcd;
}2.3 例题
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug(x) cout << #x << " = " << x << '\n'
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
int n, a, b, x, y;
int exgcd(int a, int b, int &x, int &y) //扩展欧几里得算法
{
if(b == 0) //b为0时结束递归
{
x = 1; //ax+by=a->x=1,y=0
y = 0;
return a;
}
int gcd = exgcd(b, a%b, y, x); //递归求x'和y'
y -= (a/b) * x; //此时递归后x=y',y=x',将y=x'-(a/b)y'转为y=y-(a/b)x得y-=(a/b)x
return gcd;
}
void solve()
{
cin >> n;
for(int i = 0;i < n; i++)
{
cin >> a >> b;
exgcd(a, b, x, y);
cout << x << " " << y << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t = 1;
// cin >> t;
while (t--)
solve();
return 0;
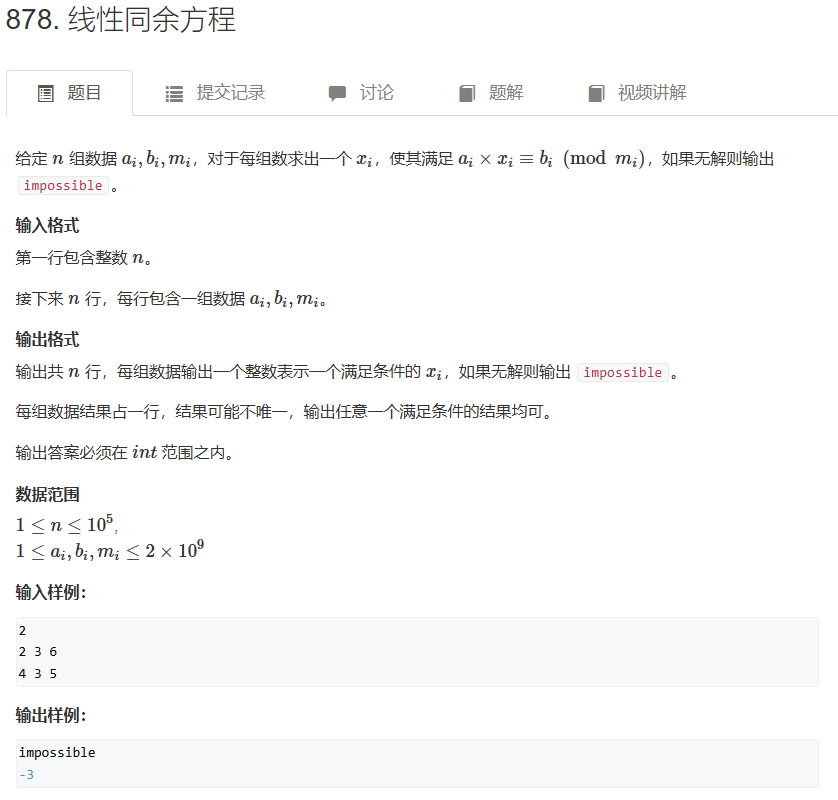
}三、线性同余方程
3.1 概念
线性同余方程ax ≡ b(mod m),要求我们求出一个整数x,使得a和x的乘积模上m等于b
对于这个方程,可以用拓展欧几里得算法求解:
- ax ≡ b(mod m)可转化为对于整数x,存在整数y使得ax = my + b
- 令y' = -y,则上式转化为ax + my' = b
- 用拓展欧几里得算法求ax' + my' = gcd(a, m)
- 只要b是gcd(a, m)的倍数则说明方程成立,整数x存在,x = x' * (b / gcd(a, m))
3.2 例题
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
#define debug(x) cout << #x << " = " << x << '\n'
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
int n, a, b, m, x, y;
int exgcd(int a, int b, int &x, int &y) //扩展欧几里得算法
{
if(b == 0) //b为0时结束递归
{
x = 1; //ax+by=a->x=1,y=0
y = 0;
return a;
}
int gcd = exgcd(b, a%b, y, x); //递归求x'和y'
y -= (a/b) * x; //此时递归后x=y',y=x',将y=x'-(a/b)y'转为y=y-(a/b)x得y-=(a/b)x
return gcd;
}
void solve()
{
cin >> n;
for(int i = 0;i < n; i++)
{
cin >> a >> b >> m;
int gcd = exgcd(a, m, x, y);
if(b % gcd == 0) //b是gcd倍数:成立
cout << x * (b / gcd) % m << endl; //为什么要%m?因为可以保证x在int范围内且同余b
else //b不是gcd倍数:无解
cout << "impossible" << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t = 1;
// cin >> t;
while (t--)
solve();
return 0;
}完.