图论-最短路-专题

题目列表

最短路
稍微进阶一点的最短路
分层最短路
- 1.HDU - 4725 The Shortest Path in Nya Graph
- 2.P4568 [JLOI2011]飞行路线

最短路

1. POJ - 3268 Silver Cow Party

题目链接：POJ - 3268 Silver Cow Party
题意：在1-N庄子各有一头牛，要去x的庄子参加派对，求一头牛来回最长时间，每头牛走最短时间
分析：每头牛走最短的路径，花费最短时间，找到来回时间最长的牛
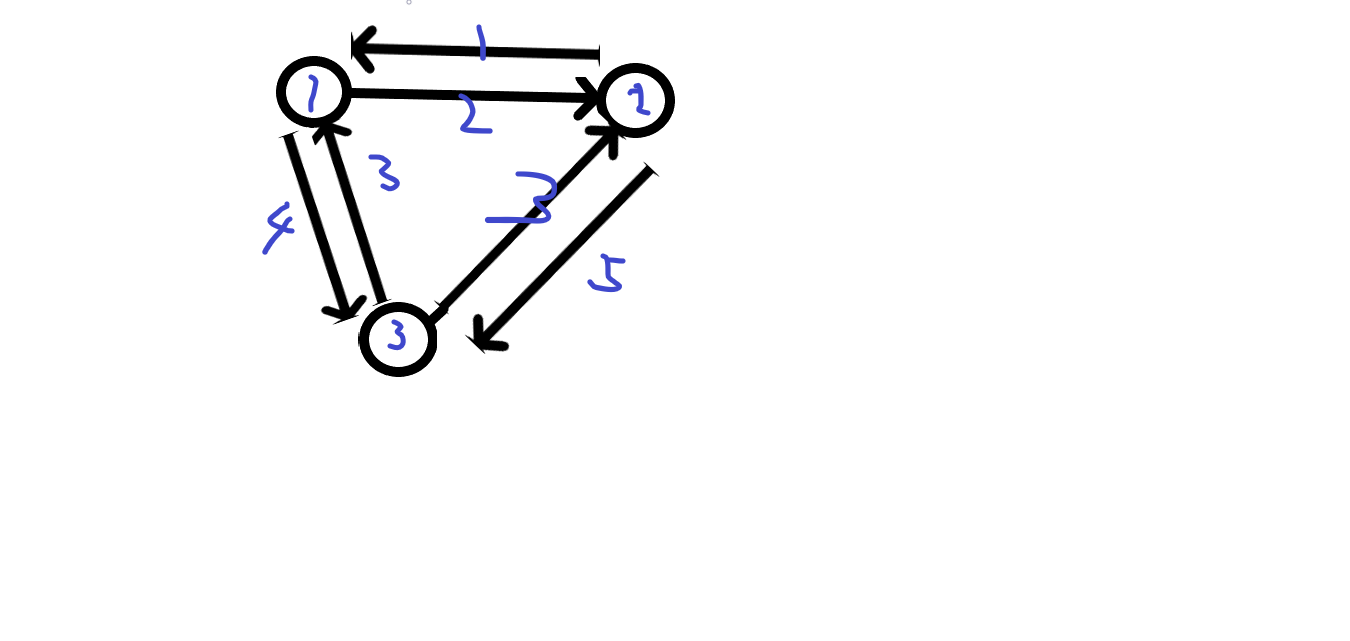
使用Dijkstra跑一遍单源最短路找到每头牛派对结束从x回到i的最短时间，然后将所有边反向，再跑一遍最短路Dijkstra，找到去参加的最短时间，每头牛求出自己的来回时间，输出最大max
ps：为什么反向再求单源最短路就是参加的时间
参加：从各个点到2的最短时间
把所有边反向后，原来指向自己的现在由自己指出
在这里插入图片描述
将所有边方向，红色是反向之后的方向

看边的指向——将从各个点到x的最短路转化为从x到各个点的最短路
所以反向之后再跑一遍Dijkstra就是各个点到x参加派对的最短时间

知识点：反向边+Dijkstra

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<cstring>

using namespace std;

const int N = 1100,M = 1e5+10;

int d[N];
bool vis[N];
int g[N][N];
int a[M],b[M],c[M];
int n,m,x;
int s[N];
int mx=0;

void rebulid()
{
    memset(g,0x3f,sizeof(g));

    for(int i=0;i<m;i++)
    {
        g[b[i]][a[i]]=min(g[b[i]][a[i]],c[i]);
    }
}
void dij()
{

    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));
    d[x]=0;
    for(int i=0;i<n;i++)
    {
        int t=-1;
        for(int j=1;j<=n;j++)
            if(!vis[j]&&(t==-1||d[j]<d[t]))t=j;

        vis[t]=true;

        for(int j=1;j<=n;j++)
            d[j]=min(d[j],d[t]+g[t][j]);
    }

}

int main()
{
    memset(g,0x3f,sizeof(g));
    scanf("%d%d%d",&n,&m,&x);

    for(int i=0;i<m;i++)
    {
        scanf("%d%d%d",&a[i],&b[i],&c[i]);
        g[a[i]][b[i]]=min(g[a[i]][b[i]],c[i]);
    }

    dij();
    for(int i=1;i<=n;i++)
    {
        s[i]+=d[i];
    }
    rebulid();
    dij();

    for(int i=1;i<=n;i++)
        s[i]+=d[i],mx=max(mx,s[i]);

    printf("%d\n",mx);

    return 0;

}

2. P4366 [Code+#4]最短路

题目链接：P4366 [Code+#4]最短路
知识点：建图+SPFA

#include<iostream>
#include<queue>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;

const int MAX = 2e5+10 , MM = 4e6+10;
typedef pair<int,int>Pair;
int d[MAX];
int vis[MAX];
int N,M,C,A,B;
int e[MM],h[MAX],ne[MM],w[MM],idx=1;
int x1,x2;

void add(int a,int b,int c)
{
    e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
}

int spfa()
{
    memset(d,0x3f,sizeof(d));
    priority_queue<Pair>q;
    q.push(Pair{0,x1});
    d[x1]=0;

    while(q.size())
    {
        int t=q.top().second;
        q.pop();
        if(vis[t])continue;
        vis[t]=true;
        if(t==x2)return d[x2];
        for(int i=h[t];i;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                q.push(Pair{-d[j],j});
            }
        }
    }
}

int main()
{
    scanf("%d%d%d",&N,&M,&C);

    while(M--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }

    int lg2=log2(N);
	for(int i=1;i<=N+(1<<lg2);i++)
    {
		for(int j=0;j<=lg2;j++)
            add(i,i^(1<<j),(1<<j)*C);
	}

    scanf("%d%d",&x1,&x2);

    printf("%d\n",spfa());

    return 0;
}

3. POJ - 3159 Candies

题目链接： POJ - 3159 Candies

题意：有n个小朋友进行分糖果，a 不想让 b 小朋友的糖果比ta多c个，满足这个条件，使小朋友的糖果数值差值尽可能大
分析：SPFA 差分分析，使差值最大，建立图，每一个小朋友是一个节点，c就是他们边的权值，寻找1-n小朋友的最大糖果差值
~~我觉得题意有点迷~~
ps：卡时间最好使用read（）快读和stack
~~发现stack好像比queue快一些~~
知识点：SPFA差分分析+建图

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<cmath>
#include<stack>

using namespace std;

const int N = 3e4+10,M = 2e5+10;

int n,m;
long long h[N],e[M],ne[M],w[M],idx;
long long d[N];
bool vis[N];

//快读
inline int read() {
	int s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch>'9') { if (ch == '-')w = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
	return s * w;
}


void add(int a,int b,int c)
{
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}

void spfa()
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));

    stack<int>q;
    q.push(1);
    vis[1]=1;
    d[1]=0;


    while(q.size())
    {
        int t=q.top();
        q.pop();
        vis[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                //cout<<j<<' '<<d[j]<<endl;
                if(!vis[j])
                {
                    vis[j]=true;
                    q.push(j);
                }
            }
        }

    }

}

int main()
{
    n = read(), m = read();
    memset(h,-1,sizeof(h));
    while(m--)
    {
        int a, b, c;
		a = read(),b=  read(), c =read();
        add(a,b,c);
    }
    spfa();
    long long mx=0;
    //cout<<d[2]<<endl;
    printf("%lld\n",d[n]);

    return 0;
}

4. POJ - 3169 Layout

题目链接：POJ - 3169 Layout
题意：有n头牛，在一排队，需要你实现排队顺序，有ml个条件，a和b互相喜欢不能相离超过c米，有md个条件，a和b互相讨厌最少相距c米
分析：差分分析+spfa+spfa负环

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<string>

using namespace std;

const int N = 1100, M =1e6+10;
int n,ml,md;
int d[N];
bool vis[N];
int h[N],e[M],ne[M],w[M],idx;
int Time[N];

void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}

int spfa()
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));
    memset(Time,0,sizeof(Time));

    queue<int>q;
    q.push(1);
    vis[1]=true;
    d[1]=0;
    Time[1]=1;

    while(q.size())
    {
        int t=q.front();
        q.pop();
        vis[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!vis[j])
                {
                    Time[j]=Time[t]+1;
                    if(Time[j]>n)return -1;//存在负环不存在这样的路径
                    vis[j]=true;
                    q.push(j);
                }
            }
        }
    }
    //for(int i=1;i<=n;i++)cout<<d[i]<<endl;
    if(d[n]==0x3f3f3f3f)return -2;//无法到达
    return d[n];
}

int main()
{
    scanf("%d%d%d",&n,&ml,&md);
    memset(h,-1,sizeof(h));

    while(ml--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }

    while(md--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(b,a,-c);
    }

    printf("%d\n",spfa());

    return 0;
}

5. POJ - 1847 Tram

题目链接：POJ - 1847 Tram

题意：目前有n个路口我在A要到B去，每一个路口有k个可以转向的路口，默认先转向第一个，问从A到B，需要转动次数
分析：这个题意有点不好理解，就是说每一个路口是一个节点，ta可以转到k个路口，除了第一个默认权值为0，其它路口权值是1（需要转向一次）我们要从A到B路口，最少转向次数，最短路问题，我是用的spfa（如果到达不了，最后判断d）
~~不晓得为啥RE好几发，改了一下输入就对~~
~~还有需要多组输入~~
知识点：SPFA+优化+读题

#include<iostream>
#include<queue>
#include<string>
#include<cstring>
#include<cstdio>

using namespace std;

const int N = 1200,M = 1e4+50;
int d[N];
int h[N],e[M],ne[M],w[M],idx;
bool vis[N];
int n,A,B;

void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}

int spfa()
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));

    queue<int>q;
    q.push(A);
    d[A]=0;
    vis[A]=true;

    while(q.size())
    {
        int t=q.front();
        q.pop();
        vis[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];

                if(!vis[j])
                {

                    vis[j]=true;
                    q.push(j);
                }
            }
        }

    }
    if(d[B]==0x3f3f3f3f)return -1;
    return d[B];
}

int main()
{
    while(scanf("%d%d%d",&n,&A,&B)!=EOF)
    {

        memset(h,-1,sizeof(h));
        memset(e,0,sizeof(e));
        memset(ne,0,sizeof(ne));
        memset(w,0,sizeof(w));
        idx=0;
        int t,x;
        for(int i=1;i<=n;i++)
        {

            scanf("%d",&t);
            for(int j=1;j<=t;j++)
            {
                scanf("%d",&x);
                if(j==1)add(i,x,0);
                else add(i,x,1);
            }
        }

        printf("%d\n",spfa());
    }

    return 0;
}
/*
3 2 1
2 1 3
2 3 1
2 1 2
0
3 2 1
2 1 3
2 3 1
1 2
1
*/

6. POJ - 1062 昂贵的聘礼

题目链接：POJ - 1062 昂贵的聘礼

题意：你要迎娶部落公主，酋长要你彩礼p个金币，但是如果你拿物品来换就少一些金币，然后目前有n件物品，每一个物品主人等级为L，并且有x个替代品-金币，然后因为这个部落具有等级制度，不能和超过m的等级的交换东西，只要和相差超过m等级的人交换了，就不可以和高等级的人交换，你想要用最少的金币来迎娶公主

分析：使用spfa算法来求解最短路
首先是建图的问题，将我自己设为0点，我对每一个物品都有边，权值就是物品的价格，后面每个物品是一个节点，替代品t和价值v，每个替代品指向当前物品，权值就是v，可以用后面的来代替，最后构成一个指向1的图，找到一条最短路径到达1，也就是找到最少金币达到酋长的条件
其次在实际种求解，还有一个等级问题，因为m的值比较小，枚举可以进行交换物品区间，一定要包含酋长所处的等级Level，[Level-m,level]到[Level,level+m] 找到最小d[1]

知识点：SPFA+建图

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>

using namespace std;

const int N = 1010,M = 1e4+10;
int d[N];
int h[N],e[M],ne[M],w[M],idx;
bool vis[N];
int l[N];
int n,m;

void add(int a,int b,int c)
{
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}

int spfa(int left,int right)
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));

    queue<int>q;
    q.push(0);
    d[0]=0;
    vis[0]=true;//自己先放入

    while(q.size())
    {
        int t=q.front();
        q.pop();
        vis[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(l[j]<left||l[j]>right)continue;//超过等级限制，不能进行交换
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!vis[j])
                {
                    vis[j]=true;
                    q.push(j);
                }
            }
        }
    }
    return d[1];
}

int main()
{
    scanf("%d%d",&m,&n);
    memset(h,-1,sizeof(h));
    for(int i=1;i<=n;i++)
    {
        int p,le,x;
        scanf("%d%d%d",&p,&le,&x);
        add(0,i,p);//自己对每个物品都有一条边
        l[i]=le;
        for(int j=1;j<=x;j++)
        {
            int t,v;
            scanf("%d%d",&t,&v);
            add(t,i,v);
        }
    }

    int s=0x3f3f3f3f;

    for(int i=l[1]-m;i<=l[1];i++)
    {
        s=min(s,spfa(i,i+m));
    }
    printf("%d\n",s);
    return 0;
}

7. LightOJ - 1074 Extended Traffic

题目链接： LightOJ - 1074 Extended Traffic

题意：每个路口的拥挤度为ai，然后有m条路，将路口连接起来，费用是（终点的拥挤度-起点的拥挤度）^3,最终 q 个询问，输出x路口的最少收入（收入小于3或无法到达输出？）

分析：首先建图，每个路口是一个节点，每条路是边，权值是上述费用，找到一条费用最少的路，也就是最短路问题
两种输出？的情况

存在负环，则一定费用小于3，所以输出？
无法到达，跑spfa d[x]一定为0x3f3f3f3f ，也输出？

关于负环处理：若存在负环，利用染色法思想，将这个点相关都标为1全部染色，遇到染色的直接跳过，（负环-费用小于3，跑dfs标记）
ps：多组输入输出，各个数组初始化 ~~idx=0~~

知识点：SPFA+SPFA负环+染色法

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>

using namespace std;

const int N = 300,M = 1e5+10;
int d[N];
int h[N],w[M],ne[M],e[M],idx;
bool vis[N],col[N];
int t,n,m,q,c=0;
int Time[N];

void init()
{
    memset(Time,0,sizeof(Time));
    memset(h,-1,sizeof(h));
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));
    memset(col,0,sizeof(col));
    idx=0;
}

void add(int a,int b,int c)
{
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}

void dfs(int x)//将与j相连的点标记
{
    col[x]=true;
    for(int i=h[x];~i;i=ne[i])
    {
        int j=e[i];
        if(!col[j])dfs(j);
    }

}
int spfa()
{
    queue<int>q;
    q.push(1);
    vis[1]=true;
    Time[1]=1;
    d[1]=0;

    while(q.size())
    {
        int t=q.front();
        q.pop();
        vis[t]=false;
        if(col[t])continue;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                Time[j]=Time[t]+1;
                if(!vis[j])
                {
                    if(Time[j]>n)dfs(j);//存在负环 则将j所在的图费用都小于3
                    q.push(j);
                    vis[j]=true;
                }
            }
        }
    }
}


int main()
{
    scanf("%d",&t);
    int a[300],da[300];
    while(t--)
    {
        init();
        scanf("%d",&n);
        for(int i=1;i<=n;i++)scanf("%d",&a[i]);
        scanf("%d",&m);
        for(int i=1;i<=m;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            int c=a[y]-a[x];
            add(x,y,c*c*c);
            //cout<<x<<' '<<y<<c*c*c<<endl;
        }
        spfa();
//        for(int i=1;i<=n;i++)
//            cout<<'+'<<d[i]<<' '<<col[i]<<endl;
        scanf("%d",&q);
        for(int i=0;i<q;i++)
        {
            int x;
            scanf("%d",&x);
            if(d[x]<3||d[x]==0x3f3f3f3f||col[x])da[i]=-1;
            else da[i]=d[x];
        }
        printf("Case %d:\n",++c);
        for(int i=0;i<q;i++)
        {
            if(da[i]==-1)printf("?\n");
            else printf("%d\n",da[i]);
        }
    }

    return 0;
}

8. HDU - 4725 The Shortest Path in Nya Graph

题目链接：HDU - 4725 The Shortest Path in Nya Graph

题意：这是一个裸的最短路问题，有n层每层一个节点，上下两层的两个节点可以花费c代价，然后m条边，连接a和b，代价是c，询问从节点1到节点n的最少花费

分析：我开始想的太简单，直接每两个节点建边，然后RE了，然后一想n^2+m的边，太大了，数组开小了，不能直接建边，需要中间建立一个中间节点，用空间来节约时间
建好图，之后就跑一遍堆优化的Dijkstra

知识点：堆优化 Dijkstra+建图

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstring>
#include<cstdio>

using namespace std;

const int N = 2e5+1000,M = 8e5+10;
int d[N];
int h[N],e[M],w[M],ne[M],idx;
bool vis[N];
int t,n,m,C,k=0;

typedef struct Node{
    int v,d;
    Node(int d, int v):d(d), v(v) {}
	bool operator < (const Node&w) const
    {
		return d > w.d;
	}
}Node;

void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}

int spfa()
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));

    priority_queue<Node>q;
    q.push(Node{0,1});
    d[1]=0;

    while(q.size())
    {
        Node t=q.top();
        q.pop();
        if(vis[t.v])continue;
        vis[t.v]=true;
        if(t.v==n)return d[n];


        for(int i=h[t.v];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t.v]+w[i])
            {
                d[j]=d[t.v]+w[i];
                q.push(Node{d[j],j});

            }
        }
    }
    if(d[n]==0x3f3f3f3f)return -1;
    return d[n];
}

int main()
{
    scanf("%d",&t);

    while(t--)
    {
        memset(h,-1,sizeof(h));
        memset(e,0,sizeof(e));
        memset(ne,0,sizeof(ne));
        memset(w,0,sizeof(w));

        idx=0;

        scanf("%d%d%d",&n,&m,&C);
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            add(x+n,i,0);
            add(i,x+n+1,C);
            add(x+n+1,i,C);
            if(x!=1)
            {
                add(i,x+n-1,C);
                add(x+n-1,i,C);
            }
        }

        while(m--)
        {
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            add(x,y,z);
            add(y,x,z);
        }

        printf("Case #%d: %d\n",++k,spfa());

    }
    return 0;
}

9. P1119 灾后重建

P1119 灾后重建
题意：n个村庄，m条路（双向通路），但是每个村庄有经历了灾害，只有经历t才可以通行，q次询问x到y的最短路径，若不能到达输出-1
分析：仔细体会Floyd
Floyd – 使用其它点进行中转找到 i 到 j 最短路
那就会发现经历k天可以通过ai村庄也就是说经历k天前i村庄可以作为中转点找最短路（这个题数据给的比较好，k是递增的，每次只需要将新中转点进行更新最短距离）
最后问题就转化为，当时间到达t天，新修好的村庄作为可以中转的点对最短路进行更新
知识点：Floyd
~~是一个比较好的Floyd题~~

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

const int N = 210;
int d[N][N];
int Time[N];
int n,m,k;

int main()
{
    scanf("%d%d",&n,&m);
    memset(d,0x3f,sizeof(d));
    for(int i=0;i<n;i++)d[i][i]=0;
    for(int i=0;i<n;i++)scanf("%d",&Time[i]);

    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        d[a][b]=min(d[a][b],c);
        d[b][a]=min(d[b][a],c);
    }

    scanf("%d",&k);
    int index=0,day=0;
    while(k--)
    {
        int x,y,t;
        scanf("%d%d%d",&x,&y,&t);
        if(Time[x]>t||Time[y]>t)
        {
            puts("-1");
            continue;
        }
        while(Time[day]<=t&&day<n)day++;
        //day--;
        //cout<<"++++"<<day<<endl;

        for(int o=index;o<day;o++)
        {
            for(int i=0;i<n;i++)
            {
                for(int j=0;j<n;j++)
                {
                    d[i][j]=min(d[i][j],d[i][o]+d[o][j]);
                }
            }
        }

        if(d[x][y]>=0x3f3f3f3f/2)puts("-1");
        else printf("%d\n",d[x][y]);
        index=day;
    }

    return 0;
}

10.P1522 [USACO2.4]牛的旅行 Cow Tours

题目链接：P1522 [USACO2.4]牛的旅行 Cow Tours

题意：给n个农场的坐标，和他们的连接邻接矩阵，加一条边，使得最远的两个点的距离最小
分析：在一个图中增加一条边

跑最短路 Floyd 先不能连边，找到各个点到达其它点的最小距离
在各个点找他们与其它点最大距离
枚举不相连的两个点寻找最小距离
最后答案与原来的最远进行比较 max是答案
知识点：Floyd

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>

using namespace std;

const int N = 200;
double inf = 1e6;
struct Pair
{
    int x,y;
};
char a[N][N];
double d[N][N],l[N],lenmax=0,lmax=inf;
int n;
Pair point[N];

double S(int x1,int y1,int x2,int y2)
{
    double x=max(x1,x2)-min(x1,x2);
    double y=max(y1,y2)-min(y1,y2);
    return sqrt(x*x+y*y);
}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d%d",&point[i].x,&point[i].y);

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            char e;
            cin>>e;
            if(e=='1')d[i][j]=S(point[i].x,point[i].y,point[j].x,point[j].y);
            else if(i!=j)d[i][j]=inf;
            //cout<<e<<endl;
        }
    }

    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        if(d[i][j]!=inf)l[i]=max(l[i],d[i][j]);
        lenmax=max(l[i],lenmax);
    }

    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        if(i!=j&&d[i][j]==inf)
        {
            lmax=min(l[i]+S(point[i].x,point[i].y,point[j].x,point[j].y)+l[j],lmax);
        }
    printf("%.6f\n",max(lmax,lenmax));
    return 0;
}

稍微进阶一点的最短路

1. P4467 [SCOI2007]k短路

题目链接：P4467 [SCOI2007]k短路

题意：一个裸的最短路，但是不是问a到b的最短路，是问，a到b的第k条最短路

分析：最短路+A算法
A算法可以理解为一种优化剪枝的广搜，它比较的是代价函数，g(x)=d(x)+h(x),当前代价=走到当前已经花费的代价+估计代价
先反向建图，跑一遍最短路 spfa—每一个点到终点的最少花费作为各个带你的估价h(x)
后使用A* 算法进行广搜，用优先队列维护队列，找到第k短路

~~有一个测试点会MLE(A*空间爆了）看了题解特判过了这个点~~

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<string>
#include<algorithm>

using namespace std;

const int N =100,M = 10010;

int h[N],e[M],ne[M],w[M],idx;
int h1[N],e1[M],ne1[M],w1[M],idx1;
int d[N];
bool vis[N];
int n,m,k,a,b;
bool f[N];

struct Node
{
    int index;//当前节点
    int d;//到节点代价
    int g;//到终点所有代价 已花费代价+估计代价
    vector<int>s;//路径
    Node()
    {

    }
    bool operator < (const Node &b) const
    {//重载
        if (g != b.g) return g > b.g;
        int sz = min(s.size(), b.s.size());
        for (int i = 0; i < sz; i++) {
            if (s[i] != b.s[i]) return s[i] > b.s[i];
        }
        return s.size() > b.s.size();
    }

};

void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}

void add1(int a,int b,int c)
{
    e1[idx1]=b;
    w1[idx1]=c;
    ne1[idx1]=h1[a];
    h1[a]=idx1++;
}


void spfa()
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));
    queue<int>q;
    q.push(b);
    vis[b]=true;
    d[b]=0;

    while(q.size())
    {
        int t=q.front();
        q.pop();
        vis[t]=false;
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!vis[j])
                {
                    q.push(j);
                    vis[j]=true;
                }
            }
        }
    }

}


bool bfs()
{
    priority_queue<Node>q;
    Node x;
    x.index=a;
    x.d=0;
    x.g=d[a];
    x.s.push_back(a);
    q.push(x);


    while(q.size())
    {
        Node t=q.top();
        q.pop();

        if(t.index==b)
        {
            k--;
            if(k==0)
            {
                int l=t.s.size();
                for(int i=0;i<l;i++)
                {
                    if(i==0)
                    printf("%d",t.s[i]);
                    else printf("-%d",t.s[i]);
                }
                printf("\n");
                return true;
            }
        }

        for(int i=h1[t.index];i!=-1;i=ne1[i])
        {
            int j=e1[i];
            int l=t.s.size();
            bool flag=false;
            for(int k=0;k<l;k++)
            {
                if(t.s[k]==j)
                {
                    flag=true;
                    break;
                }
            }
            if(flag)continue;

            Node x=t;
            x.index=j;
            x.d=t.d+w1[i];
            x.g=x.d+d[j];
            x.s.push_back(j);
            q.push(x);
            //q.push(Node{j,t.d+w[i],t.d+w[i]+d[j],t.s+fan(j)});
        }

    }
    return false;
}

int main()
{
    scanf("%d%d%d%d%d",&n,&m,&k,&a,&b);
    memset(h,-1,sizeof(h));
    memset(h1,-1,sizeof(h1));

    for(int i=0;i<m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add(y,x,z);
        add1(x,y,z);
    }
    if(n==30&&m==759)//MLE 特判
    {
        cout << "1-3-10-26-2-30" << endl;
        return 0;
    }
    spfa();

    if(!bfs())puts("No");

    return 0;
}

2. P2483 【模板】k短路 / [SDOI2010]魔法猪学院

题目链接：P2483 【模板】k短路 / [SDOI2010]魔法猪学院

题意：有S的能量，n条路，最多可以实现几条路从1到达n，每次最小花费能量
分析：和上面k短路类似

A算法可以理解为一种优化剪枝的广搜，它比较的是代价函数，g(x)=d(x)+h(x),当前代价=走到当前已经花费的代价+估计代价
先反向建图，跑一遍最短路 spfa—每一个点到终点的最少花费作为各个带你的估价h(x) 后使用A
算法进行广搜，用优先队列维护队列，找到第k短路

~~使用A和最短路会爆栈，最后是特判过了 A比较耗内存~~

#include<iostream>
#include<algorithm>
#include<queue>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>

using namespace std;

const int N = 5001, M =2e5+1;
int h[N],e[M],ne[M],idx;
int hh[N],ee[M],nne[M],iidx;
double d[N],w[M],ww[M];

int n,m;
double S;

struct Node
{
    int index;
    double d;
    double g;
    bool operator < (const struct Node & u)const
    {
        return g>u.g;//最短
    }

};


void add(int a,int b,double c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}

void aadd(int a,int b,double c)
{
    ee[iidx]=b;
    ww[iidx]=c;
    nne[iidx]=hh[a];
    hh[a]=iidx++;
}

void spfa()
{
    for(int i=1;i<=n;i++)d[i]=1e17;
    bool vis[N];
    for(int i=1;i<=n;i++)vis[i]=0;

    queue<int>q;
    q.push(n);
    vis[n]=1;
    d[n]=0;
    while(q.size())
    {
        int t=q.front();
        vis[t]=false;
        q.pop();

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!vis[j])
                {
                    q.push(j);
                    vis[j]=true;
                }
            }
        }
    }
}

int bfs()
{
    priority_queue<Node>q;
    int c=0;
    Node x;
    x.index=1;
    x.d=0;
    x.g=d[1];
    q.push(x);

    while(q.size())
    {
        Node t=q.top();
        q.pop();
        if(t.d>S)return c;
        if(t.index==n)
        {
            //cout<<t.g<<"  "<<S<<endl;
            S-=t.g;
            c++;
            if(S<0)return c-1;
            continue;
        }

        for(int i=hh[t.index];i!=-1;i=nne[i])
        {
            int j=ee[i];
            Node x;
            x.index=j;
            x.d=t.d+ww[i];
            x.g=x.d+d[j];
            q.push(x);
        }

    }
    return c;
}

int main()
{
    scanf("%d%d%lf",&n,&m,&S);
    memset(h,-1,sizeof(h));
    memset(hh,-1,sizeof(hh));
    int xx=0;
    for(int i=0;i<m;i++)
    {
        int x,y;
        double z;
        scanf("%d%d%lf",&x,&y,&z);
        if(i==0)xx=x;
        add(y,x,z);
        aadd(x,y,z);
    }
    if (S == 10000000&&xx!=1245&&xx!=1042)
    {
        printf("2002000\n");
        return 0;
    }
    if (S == 10000000&&xx==1042)
    {
        printf("104180\n");
        return 0;
    }
    spfa();

    printf("%d\n",bfs());

    return 0;
}

3. P1462 通往奥格瑞玛的道路

题目链接：P1462 通往奥格瑞玛的道路

题意：从1走到n 有m条路，走过第i条路，a和b 消耗c血量（双向路），然后路过一个城市就需要给过路费f，求每次经过的城市收费最大值的最小值

分析：一看到最大值的最小值就i想到二分答案，mid 每次寻一遍最短路是不是通过小于mid的城市过路费最大值，是否可以活着到达n城市（血量>=0)

知识点：二分+最短路（SPFA）


#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#include<vector>

using namespace std;

const int N =1e4+10,M = 1e5+10;
typedef pair<int,int>Pair;
int h[N],e[M],ne[M],w[M],idx;
int n,m,b;
int d[N],mon[N];
bool vis[N];

void add(int a,int b,int c)
{
    e[idx]=b;
    w[idx]=c;
    ne[idx]=h[a];
    h[a]=idx++;
}


bool spfa(int x)
{
    memset(d,0x3f,sizeof(d));
    memset(vis,0,sizeof(vis));
    d[1]=0;
    queue<int>q;
    q.push(1);
    vis[1]=true;

    while(q.size())
    {
        int t=q.front();
        q.pop();
        vis[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(mon[j]>x)continue;
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!vis[j])
                {
                    vis[j]=true;
                    q.push(j);
                }
            }
        }
    }
    if(d[n]>b)return false;
    return true;
}

int main()
{
    int l=1e9,r=0;
    scanf("%d%d%d",&n,&m,&b);

    for(int i=1;i<=n;i++)scanf("%d",&mon[i]),l=min(l,mon[i]),r=max(r,mon[i]);

    memset(h,-1,sizeof(h));
    for(int i=0;i<m;i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
        add(b,a,c);
    }
    //cout<<r<<endl;
    if(!spfa(r+1))
    {
        printf("AFK\n");
        return 0;
    }

    while(l<r)
    {
        int mid=(l+r)/2;
        if(spfa(mid))r=mid;
        else l=mid+1;
    }

    printf("%d\n",l);
    return 0;
}

分层最短路

分层图最短路是在多个平行的图进行决策，在每个图建立权值0的边进行转换

一般模型是：在一个正常的图上可以进行 k
次决策，对于每次决策，不影响图的结构，只影响目前的状态或代价。一般将决策前的状态和决策后的状态之间连接一条权值为决策代价的边，表示付出该代价后就可以转换状态了。

直接看题

1.HDU - 4725 The Shortest Path in Nya Graph

题目链接：HDU - 4725 The Shortest Path in Nya Graph

题意：n个点，m条边，每个点在一层，如果进行上下层的移动则只需要花费c代价，问从1到n的最代价

分析：开始一看以为是一个裸的最短路,一看数据范围 $0 <= N, M <= 10^5)$
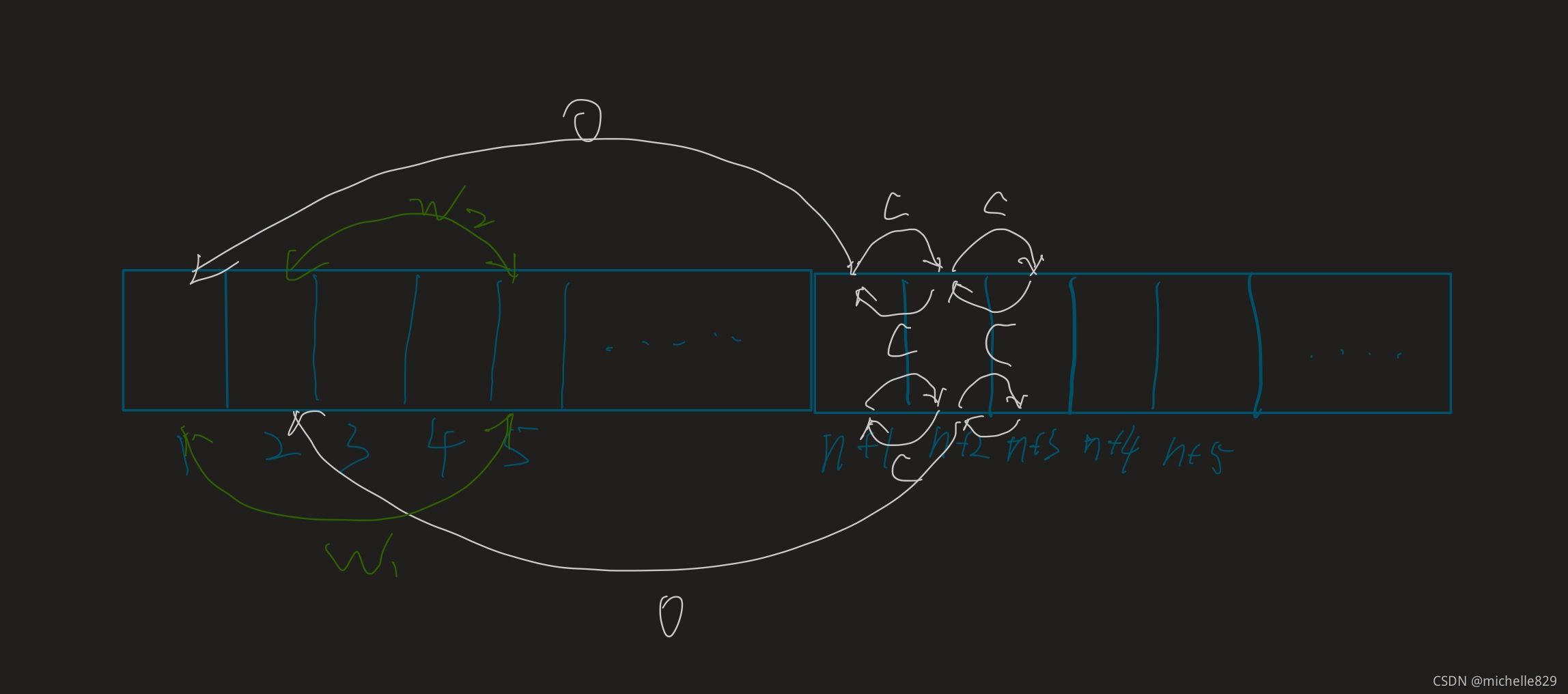
肯定不是了，如果按照题目建边，太多了边，所以要考虑怎么建图
将每层抽象为一个点，扩展点为n+1~n+n

这样可以将边减少为边为c的边减少为5n，再加上w代价的边2n，一共7*n条边建立
建好图，之后就是跑个spfa的板子，找到最短路

知识点：spfa+分层建图

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>

using namespace std;

const int N =2e5+10,M = 7e5+10;
int h[N],ne[M],e[M],w[M],idx;
int n,m,c,t,s;
bool st[N];
int d[N];
typedef pair<int,int>Pair;

void add(int a,int b,int c)
{
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}

int spfa()
{
    memset(st,0,sizeof(st));
    memset(d,0x3f,sizeof(d));

    priority_queue<Pair,vector<Pair>,greater<Pair>>q;
    q.push(Pair{0,1});
    st[1]=true;
    d[1]=0;
    while(q.size())
    {
        Pair x=q.top();
        int t=x.second;
        q.pop();
        st[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!st[j])
                {
                    st[j]=true;
                    q.push(Pair{d[j],j});
                }
            }
        }
    }
    if(d[n]==0x3f3f3f3f)return -1;
    return d[n];
}

int main()
{
    cin>>t;
    while(t--)
    {
        memset(h,-1,sizeof(h));

        idx=0;
        scanf("%d%d%d",&n,&m,&c);
        for(int i=1;i<=n;i++)
        {
            int x;
            scanf("%d",&x);
            add(x+n,i,0);
            add(i,x+n+1,c);add(x+n+1,i,c);
            if(x!=1)add(i,x+n-1,c),add(x+n-1,i,c);
        }
        while(m--)
        {
            int x,y,z;
            scanf("%d%d%d",&x,&y,&z);
            add(x,y,z);add(y,x,z);
        }
        int t=spfa();
        cout<<"Case #"<<++s<<": "<<t<<endl;
    }
    return 0;
}

2.P4568 [JLOI2011]飞行路线

题目链接：P4568 [JLOI2011]飞行路线

题意：n个城市，m条航线，可以有k条航班免费做，问送s城市到t城市的最少花费

分析：建k+1层图，每层图之间加入权值为0的航班，每跨越一层就是用了一次免费航班
跨越k层到最后一层t就是最小花费

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<vector>

using namespace std;

typedef pair<int,int>Pair;

const int N = 1e6+10,M= 5e6+10;
int h[N],e[M],ne[M],w[M],idx;
int n,m,k,s,t;
bool st[N];
int d[N];

void add(int a,int b,int c)
{
    e[idx]=b;
    ne[idx]=h[a];
    w[idx]=c;
    h[a]=idx++;
}

int spfa()
{
    memset(d,0x3f,sizeof(d));
    memset(st,0,sizeof(st));
    priority_queue< Pair,vector<Pair>,greater<Pair> >q;
    q.push(Pair{0,s});
    d[s]=0;
    st[s]=true;

    while(q.size())
    {
        Pair x=q.top();
        q.pop();
        int t=x.second;
        st[t]=false;

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(d[j]>d[t]+w[i])
            {
                d[j]=d[t]+w[i];
                if(!st[j])
                {
                    st[j]=true;
                    q.push(Pair{d[j],j});
                }
            }
        }

    }
    return d[t+k*n];
}

int main()
{
    cin>>n>>m>>k>>s>>t;
    memset(h,-1,sizeof(h));

    while(m--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        add(x,y,z);add(y,x,z);
        for(int i=1;i<=k;i++)
        {
            add(x+(i-1)*n,y+i*n,0);
            add(y+(i-1)*n,x+i*n,0);
            add(x+i*n,y+i*n,z);
            add(y+i*n,x+i*n,z);
        }
    }

    for(int i=1;i<=k;i++)
        add(t+(i-1)*n,t+i*n,0);

    int t=spfa();

    printf("%d",t);

    return 0;
}