一、PID概要
准确控制的核心: 反馈
适用于线性系统(二阶以内),满足齐次性、叠加性。
故,高阶系统需化二阶系统,非线性需线性化。
二、控制系统
1. 开环控制系统
- 无反馈控制系统,较易理解,系统框图略
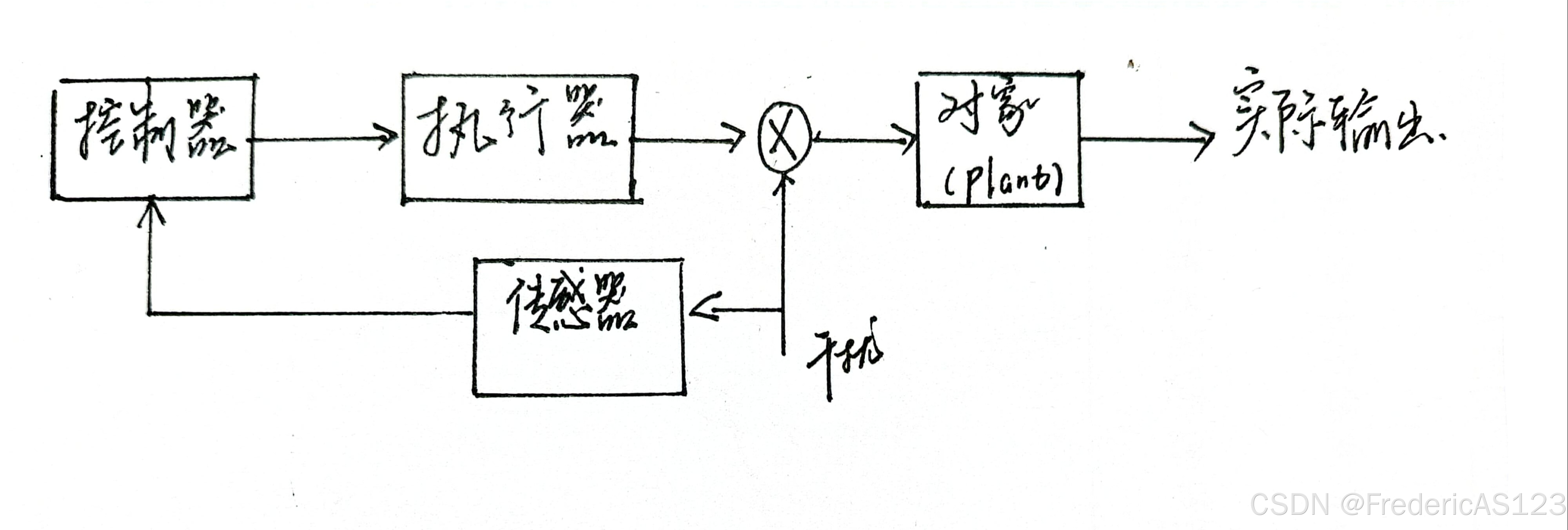
- 前馈控制系统,传感器检测干扰量。
2. 闭环控制系统
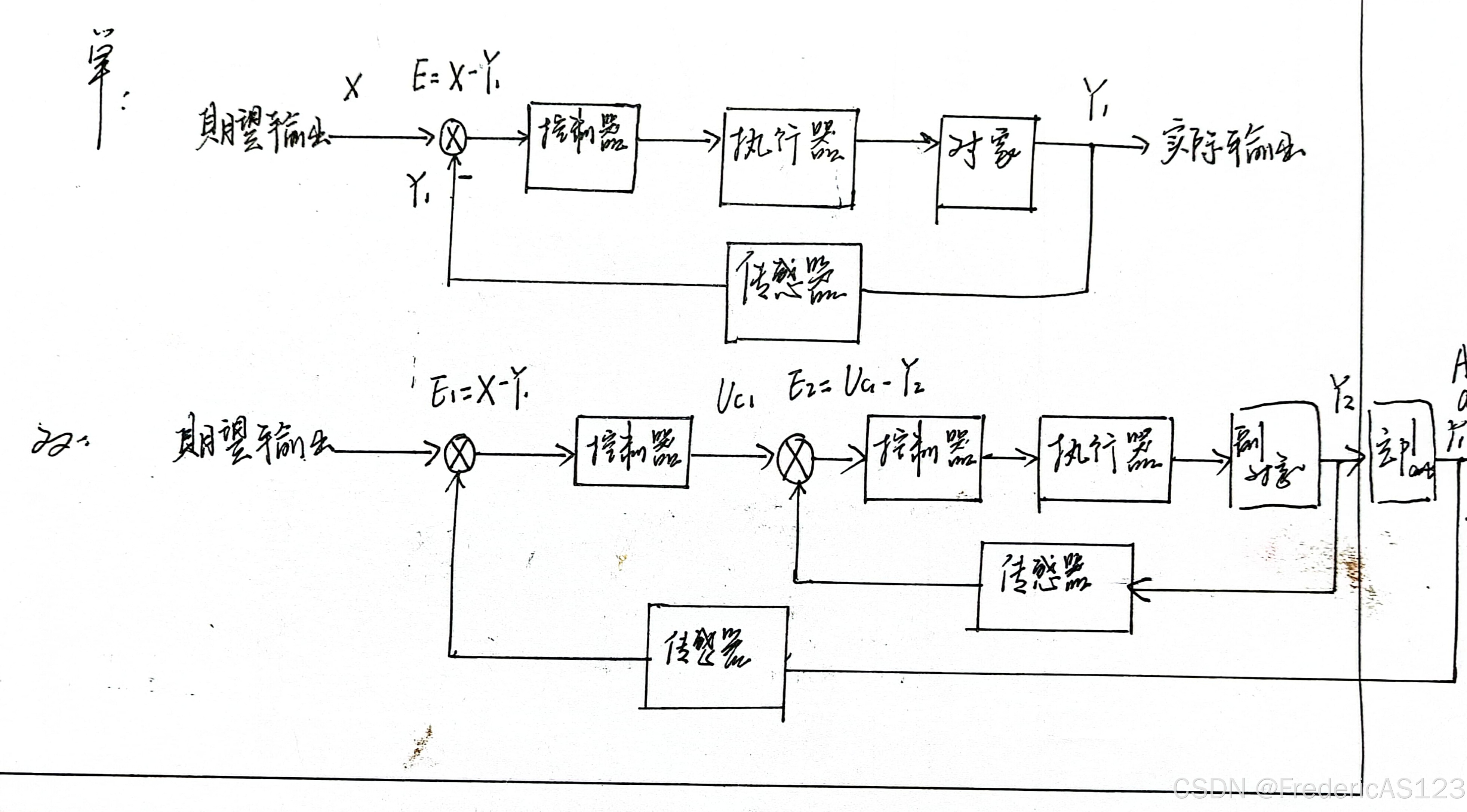
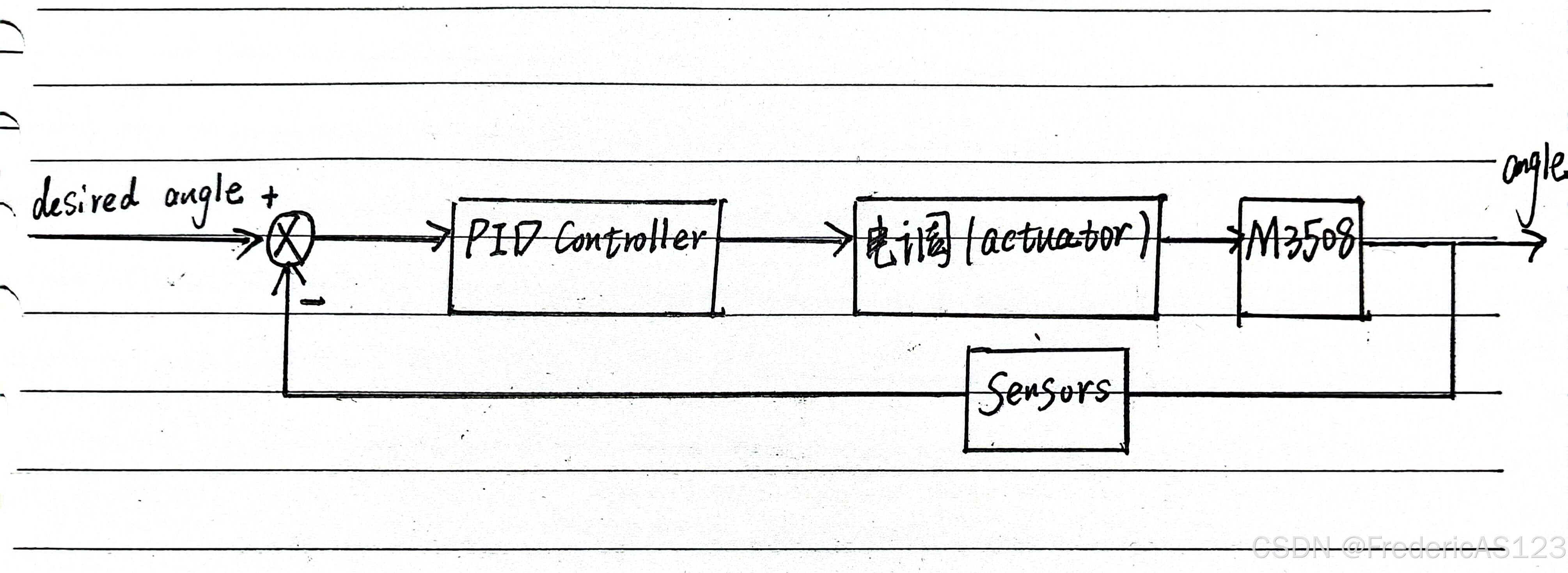
- 单环控制:传感器检测实际输出
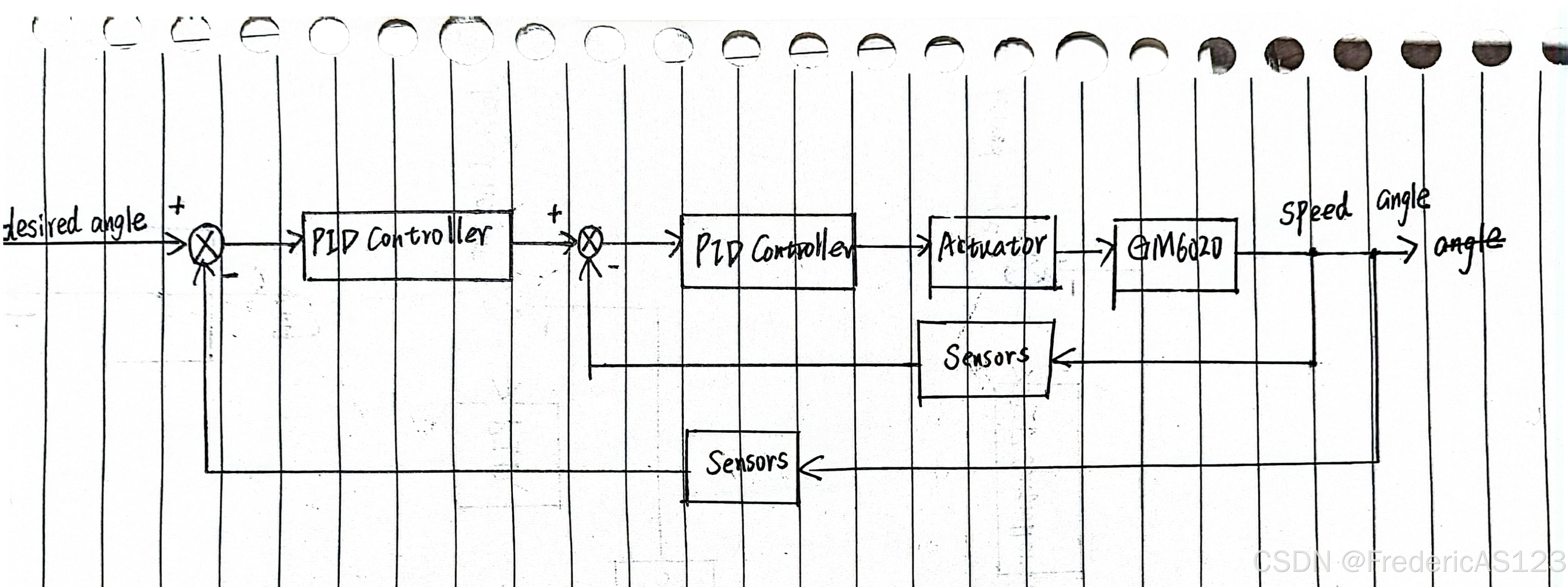
- 双环控制:相较于单环增加了内部环,使得外环控制更加容易,控制更加稳定。
home.csdnimg.cn/images/20230724024159.png?origin_url=%E5%8F%8D%E9%A6%88.jpg&pos_id=img-7pmflLLG-1727694765127)
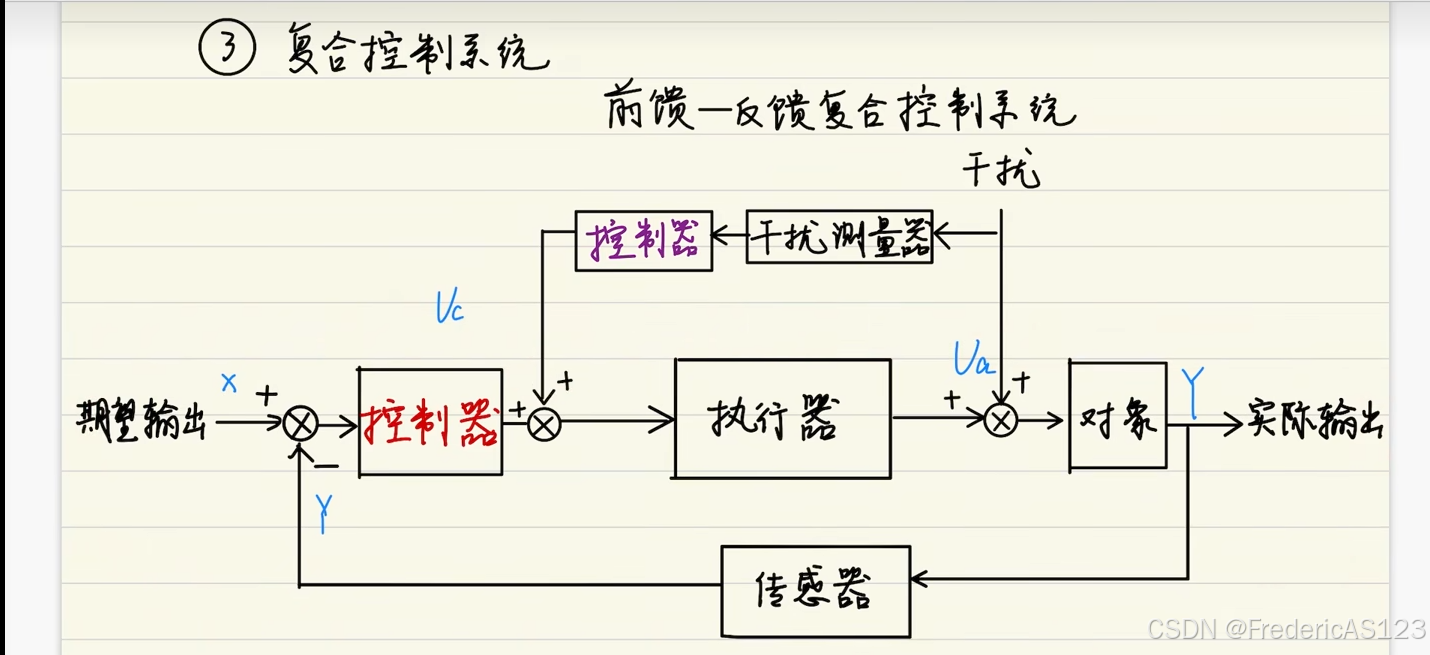
3. 复合型控制系统
综合以上两种,框图如图:
三、PID公式
内容
e
=
X
−
Y
e=X-Y
e=X−Y为偏差量。
连续
C
=
K
p
∗
e
+
K
i
∗
∫
0
t
e
d
x
+
K
d
∗
d
e
d
t
C = K_p*e+K_i*\int_{0}^{t} e \, dx+K_d*\frac{de}{dt}
C=Kp∗e+Ki∗∫0tedx+Kd∗dtde
离散
C
=
K
p
∗
e
i
+
K
i
∗
∑
n
=
0
∞
e
i
+
K
d
∗
Δ
e
i
−
Δ
e
i
−
1
Δ
t
C = K_p*e_i+K_i*\sum_{n=0}^{\infty} e_i \, +K_d*\frac{\Delta e_i-\Delta e_{i-1} }{\Delta t}
C=Kp∗ei+Ki∗n=0∑∞ei+Kd∗ΔtΔei−Δei−1
令
K
d
Δ
t
=
K
d
\frac{K_d}{\Delta t} = K_d
ΔtKd=Kd
则有:
C
=
K
p
∗
e
i
+
K
i
∗
∑
n
=
0
∞
e
i
+
K
d
∗
(
Δ
e
i
−
Δ
e
i
−
1
)
C = K_p*e_i+K_i*\sum_{n=0}^{\infty} e_i \, +K_d*(\Delta e_i-\Delta e_{i-1})
C=Kp∗ei+Ki∗n=0∑∞ei+Kd∗(Δei−Δei−1)
一般有:
P
=
K
p
∗
e
i
P = K_p*e_i
P=Kp∗ei
I
=
K
i
∗
∑
n
=
0
∞
e
i
I = K_i*\sum_{n=0}^{\infty} e_i
I=Ki∗n=0∑∞ei
D
=
K
d
∗
(
Δ
e
i
−
Δ
e
i
−
1
)
D = K_d*(\Delta e_i-\Delta e_{i-1})
D=Kd∗(Δei−Δei−1)
公式理解
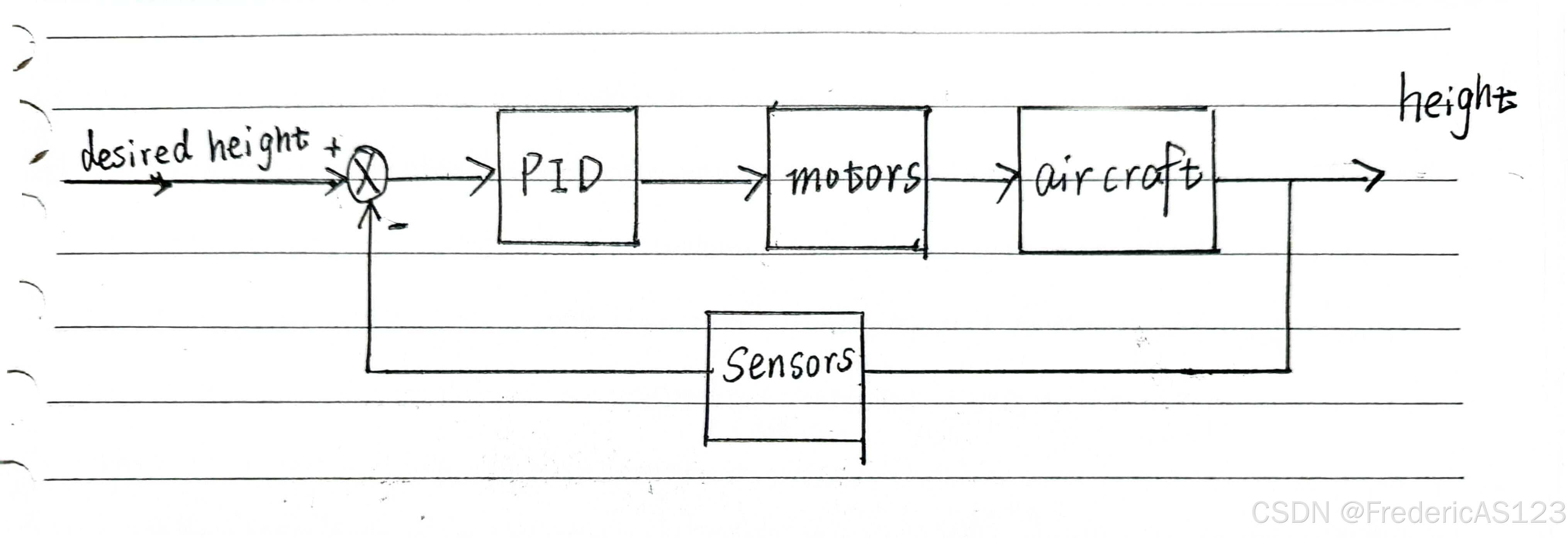
假设有一悬停的无人机,需要从地面飞到100m的高度并悬停。其控制框图应大致如下:
我们从无人机起飞到悬停整个过程试图理解PID:
- 首先,飞机需要起飞,需要动力。而且,为了让飞机快速且稳定的到达,我们希望在起飞时动力大一些,随着高度偏差量的减小,速度逐渐平稳直至悬停。因此最直接的方式就是直接将高度偏差量乘以某一系数,由控制器传给电机。这就是比例系数 K p K_p Kp。此项即为 P P P项。
- 但是,由于无人机自身的质量,它时刻都需要分出一个恒定的力来平衡重力。因此,如果只有 P P P项,由于高度偏差量最终减小至零,此时无论 K P K_P KP为多少都无法悬停,无人机始终无法悬停到目标位置。故我们仍需要一个不完全与当前时刻状态有关的量来帮助 P P P值。因此,我们想到了积分。积分是一个随时间增长的量,不完全与当前时刻状态相关。故我们引入 I I I项,定义为积分系数乘以偏差随时间的积分。
- 现在,我们可以控制无人机飞到指定高度。但我们希望对其的控制可以稳定顺滑,不希望出现突变的控制信号。为了防止控制量突变(斜率过大),当 e e e变化曲线斜率过大时,我们需要一个量去抵消此时正向的控制值,适当阻碍电机旋转。因此,我们可以使用微分的概念。微分可以体现变化快慢,且在未达到预期悬停高度时,变化率均为负数,可以减缓变化。故引入 D D D值。
- 三者相加,即为最终公式
此时,PID控制器可看作是P控制器,I控制器和D控制器三者并联。
特殊情况处理
- 场景一:当无人机起飞时,有人用手将无人机固定在原位不动。此时
e
i
e_i
ei持续积分,
I
I
I值持续增大。当积累一定时间后,一旦松手,由于
I
I
I值已被积累到巨大值,飞机将以不可控的加速度上升,造成危险。
解决方案:积分限幅。限制 I I I值的最大值,当到达 I m a x I_{max} Imax后, I I I值不再增加。 - 场景二:无人机需要悬停高度太高,
e
i
e_i
ei积分过大。快到达悬停点时由于
I
I
I值过大,导致无人机仍以较大速度上升,容易造成超调。
解决方案:积分分离。同样的,当 e i e_i ei超过某值时 I I I值停止积分。