目录

题目

格式

样例

代码

反思

题目

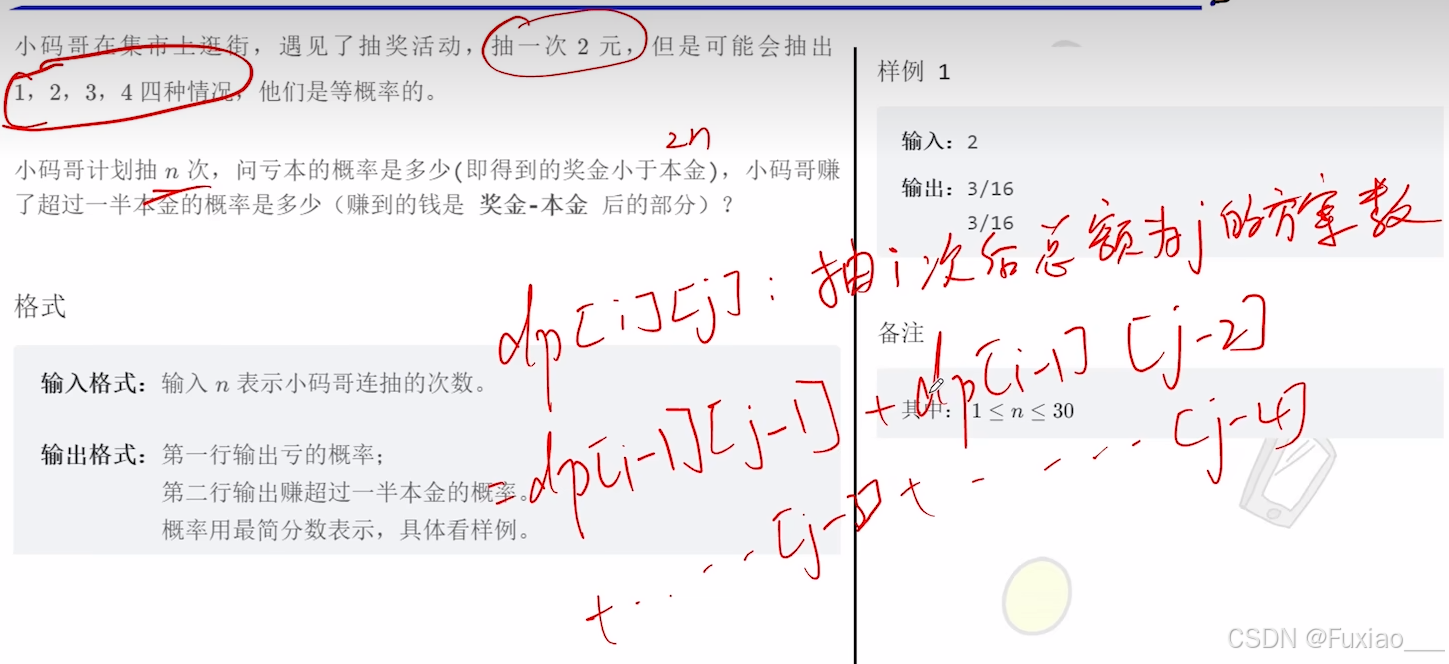
小码哥在集市上逛街，遇见了抽奖活动，抽一次2元，但是可能会抽出1，2，3，4四种情况，他们是等概率的。
小码哥计划抽n 次，问亏本的概率是多少(即得到的奖金小于本金)，小码哥赚了超过一半本金的概率是多少（赚到的钱是奖金-本金后的部分)?

格式

输入格式:输入n表示小码哥连抽的次数。
输出格式:第一行输出亏的概率;
第二行输出赚超过一半本金的概率。概率用最简分数表示，具体看样例。

样例

输入：

2

输出：

3/16
3/16

思路

状态转移方程如上，而初始的条件为（第一次，抽到四种情况的方案数均为1）：

 dp[1][1]=dp[1][2]=dp[1][3]=dp[1][4]

代码

#include <bits/stdc++.h>
using namespace std;
//第一次提交只过了一半，估计是int开小了
long long dp[40][160];  //dp[i][j]表示第i次抽奖时，抽奖总数为j的方案数。
int n;
long long sum1, sum2, fenmu = 1;

int gcd(int a, int b) //因为题目要求输出为最简分数
{
	return b == 0 ? a : gcd(b, a % b);
}

int main()
{
	cin >> n;
	//首先进行初始化
	dp[1][1] = dp[1][2] = dp[1][3] = dp[1][4] = 1;
	//分母为所有情况，为4的n次方。
	fenmu = pow(4, n);
	for (int i = 1; i <=n; i++)
	{
		for (int j = i; j <= 4 * n; j++)     //这里可以改成小于4*i吗
		{
			//记住，动态规划带有更新条件！
			for (int k = 1; k <= 4; k++) //这里是对四种情况进行遍历
			{
				if (j>k)
				{
					dp[i][j] += dp[i-1][j - k];    //这个抽奖的次数要表示成上一次的，要注意减一！！！
				}
			}
		}
	}
	//接下来计算两种情况所对应的分母
	for (int i =n; i <2 * n; i++)     //这里不能等于2*n
	{
		sum1 += dp[n][i];  //当然是计算第n次抽奖的方案数啦
	}
	for (int j = 3 * n+1; j <= 4 * n; j++)
	{
		sum2 += dp[n][j];
	}
	int temp = gcd(sum1, fenmu);
	cout << sum1 / temp << "/" << fenmu / temp << endl;
	temp = gcd(sum2, fenmu);
	cout << sum2 / temp << "/" << fenmu / temp << endl;
	return 0;
}

反思

（1）注意数据类型，要开long long

（2）dp[i-1][j-k]要注意i也要减一，表示上一次抽奖！

 注：本题解题思路来源b站up主：轩哥码题，有需要可跳转B站看up详细讲解。附up链接：b站up个人主页