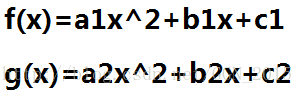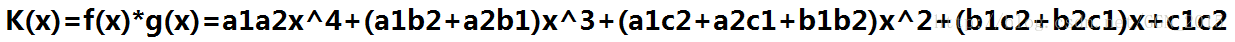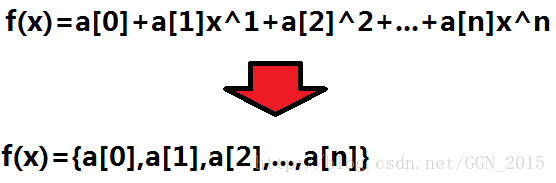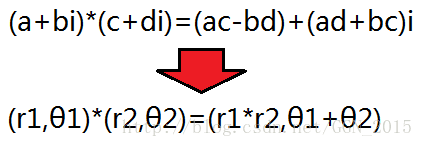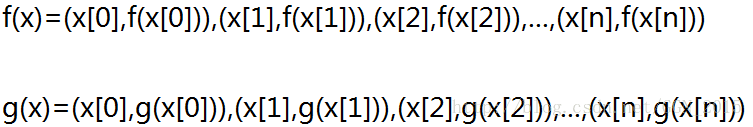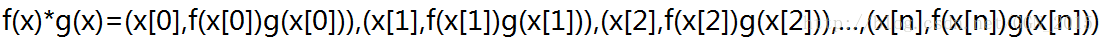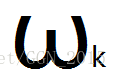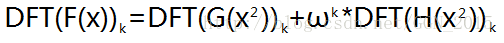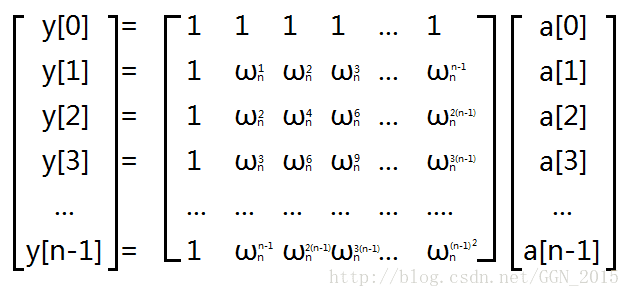FFT详解

序言

（来学习的同学们请直接跳过这里就好了…）

非常感谢Leo学长为我耐心的讲解，在此对学长表示诚挚的敬意。停课学习竞赛的那一个月里，学长们不惜耽误自己的时间为我耐心讲解算法，对我的帮助是我永难忘记的。最后衷心祝愿高三学长们在高考中取得优异的成绩！

同时我也要向学长们致歉，感谢学长们曾经对我的包容。

2017.11.19 GGN 补加序言

前言

一直想学FFT，当时由于数学基础太差，导致啥都学不懂。请教了机房里的几位学长大神，结果还是没太明白。因此下定决心写一篇关于“FFT”的文章，一篇起码我能看得懂的“FFT”。不过这好像并不是一件简单的事，因为首先我要学会“FFT”的原理。

建议同学们先自学一下“复数（虚数）”的性质、运算等知识，不然看这篇文章有很大概率看不懂。最后你就会发现，这不是一个“算法”的博客，而是一个数学的博客。

这是当时教我FFT的机房学长的博客：

Leo 的《FFT与多项式乘法》

（温馨提示：整篇文章都不是很好理解，提醒同学们保持清醒的头脑。）

1.什么是FFT？

FFT，即为快速傅氏变换，是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。它对傅氏变换的理论并没有新的发现，但是对于在计算机系统或者说数字系统中应用离散傅立叶变换，可以说是进了一大步。——360百科

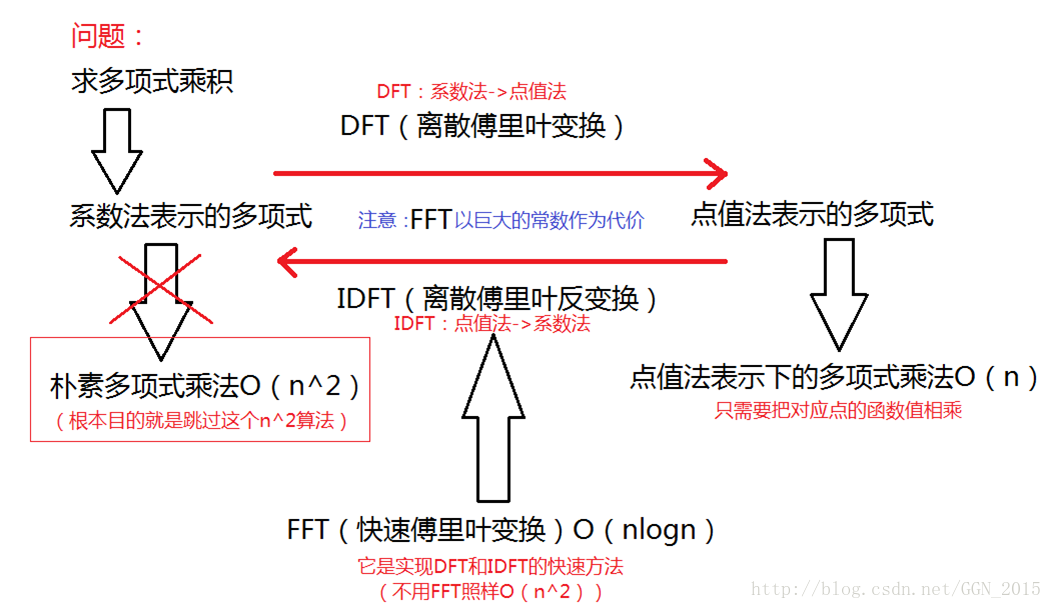
FFT（Fast Fourier Transformation）就是“快速傅里叶变换”的意思，它是一种用来计算DFT（离散傅里叶变换）和IDFT（离散傅里叶反变换）的一种快速算法。这种算法运用了一种高深的数学方式、把原来复杂度为 $O(n^2)$ 的朴素多项式乘法转化为了 $O(nlog n)$ 的算法。

2.多项式乘法的朴素算法

假设我们现在不会FFT，我们是又是如何计算多项式乘法的呢？现在我们有两个关于x的二次多项式：

f (x) = a 1 x 2 + b 1 x + c 1

$f(x)=a_1x^2+b_1x+c_1$

g (x) = a 2 x 2 + b 2 x + c 2

$g(x)=a_2x^2+b_2x+c_2$

两个二次多项式

我命令K（x）为他们的乘积，则有：

K (x) = f (x) \times g (x) = a 1 a 2 x 4 + (a 1 b 2 + a 2 b 1) x 3 + (a 1 c 2 + a 2 c 1 + b 1 b 2) x 2 + (b 1 c 2 + b 2 c 1) x + c 1 c 2

$K(x)=f(x) \times g(x)=a_1a_2x^4+(a_1b_2+a_2b_1)x^3+(a_1c_2+a_2c_1+b_1b_2)x^2+(b_1c_2+b_2c_1)x+c_1c_2$

四次多项式

如果在程序中，我们用一个数组来储存一个多项式的各个项的系数，我们如何去做这样一个复杂的乘法呢？

#include<iostream>
#include<vector>
#include<cstdlib>
using namespace std;

vector<double>ForceMul(vector<double>A,vector<double>B)//表示A,B两个多项式相乘的结果
{
    vector<double>ans;
    int aLen=A.size();//A的元素个数
    int bLen=B.size();//B的元素个数
    int ansLen=aLen+bLen-1;//ans的元素个数=A的元素个数+B的元素个数-1
    for(int i=1;i<=ansLen;i++)//初始化ans
        ans.push_back(0);
    for(int i=0;i<aLen;i++)
        for(int j=0;j<bLen;j++)
            ans[i+j]+=A[i]*B[j];//A的i次项 与 B的j次项 相乘的结果 累加到ans的[i+j]次位
    return ans;//返回ans
}

int main()
{
    vector<double>A,B;
    cout<<"input A:";
    for(int i=0;i<3;i++)//从0次项开始输入A的各项系数
    {
        int x;
        cin>>x;
        A.push_back(x);
    }
    cout<<"input B:";
    for(int i=0;i<3;i++)//从0次项开始输入B的各项系数
    {
        int x;
        cin>>x;
        B.push_back(x);
    }
    vector<double>C=ForceMul(A,B);//C=A与B暴力相乘
    cout<<"output C:";
    for(int i=0;i<5;i++)//从0次项开始输出C的各项系数
        cout<<C[i]<<" ";
    cout<<endl;
    system("pause");
    return 0;
}

这就是朴素算法,它的复杂度为O（lenA*lenB）。如果lenA=lenB=10^5，程序时间就会爆掉，那么我们如何进行优化呢？

3.系数表示法与点值表示法

系数表表示法，就是用一个多项式的各个项的系数表示这个多项式，也就是我们平时所用的表示法。例如，我们可以这样表示：

f (x) = a 0 + a 1 x + a 2 x 2 + . . + a n x n \Leftrightarrow f (x) = {a 0, a 1, a 2, . ., a n}

$f(x)=a_0+a_1x+a_2x^2+..+a_nx^n \Leftrightarrow f(x)=\{a_0,a_1,a_2,..,a_n\}$

系数表示法

点值表示法，就是把这个多项式理解成一个函数，用这个函数上的若干个点的坐标来描述这个多项式。

（两点确定一条直线，三点确定一条抛物线…同理n+1个点确定一个n次函数，其原理来自于“高斯消元”，下文会有介绍。）

因此表示成这样：（注意：x[0]->x[n]是n+1个点）

f (x) = a 0 + a 1 x + a 2 x 2 + . . + a n x n \Leftrightarrow f (x) = {(x 0, y 0), (x 1, y 1), (x 2, y 2), . ., (x n, y n)}

$f(x)=a_0+a_1x+a_2x^2+..+a_nx^n \Leftrightarrow f(x)=\{(x_0,y_0),(x_1,y_1),(x_2,y_2),..,(x_n,y_n)\}$

点至表示法

为什么n+1个确定的点能确定一个唯一的多项式呢？你可以尝试着把这n+1个点的值分别代入多项式中：

f (x 0) = y 0 = a 0 + a 1 x 0 + a 2 x 20 + . . + a n x n 0

$f(x_0)=y_0=a_0+a_1x_0+a_2x_0^2+..+a_nx_0^n$

f (x 1) = y 1 = a 0 + a 1 x 1 + a 2 x 21 + . . + a n x n 1

$f(x_1)=y_1=a_0+a_1x_1+a_2x_1^2+..+a_nx_1^n$

f (x 2) = y 2 = a 0 + a 1 x 2 + a 2 x 22 + . . + a n x n 2

$f(x_2)=y_2=a_0+a_1x_2+a_2x_2^2+..+a_nx_2^n$

. . .

$...$

f (x n) = y n = a 0 + a 1 x n + a 2 x 2 n + . . + a n x n n

$f(x_n)=y_n=a_0+a_1x_n+a_2x_n^2+..+a_nx_n^n$

带入所有点

你会得到n+1个方程，其中x[0~n]和y[0~n]是已知的，a[0~n]是未知的。n+1的未知数，n+1个方程所组成的方程组为“n+1元一次方程”，因为它是“一次方程”，所以（一般情况下，不考虑无解和无数解）可以通过“高斯消元”解得所有未知数唯一确定的值。也就是说，用点知表示法可以确定出唯一确定的系数表示法中的每一位的系数。

这种把一个多项式转化成“离散的点”表示的方法就叫做“DFT”（离散傅里叶变换）。

把“离散的点”还原回多项式的方法就叫做“IDFT”（离散傅里叶反变换）。

（请同学们重视上面的这两句话，因为这是我能想到的最好理解的解释方法了。）

有兴趣的可以看一下360百科给出的DFT定义：

离散傅里叶变换（Discrete Fourier Transform，缩写为DFT），是傅里叶变换在时域和频域上都呈离散的形式，将信号的时域采样变换为其DTFT的频域采样。在形式上，变换两端（时域和频域上）的序列是有限长的，而实际上这两组序列都应当被认为是离散周期信号的主值序列。即使对有限长的离散信号作DFT，也应当将其看作其周期延拓的变换。在实际应用中通常采用快速傅里叶变换计算DFT。——360百科

4.“复数”的引入

初中我们可能学过一些定理：比如 $\sqrt{-1}$ 不存在。但是，当时我们的“数域”仅仅止步于“实数”，而现在我们要介绍一个新的数域——“虚数”。我们令： $i=\sqrt{-1}$ 表示这个“虚数单位”，“ $i$ ”对于虚数的意义就相当于是“数字1”对于实数的意义。

这是百科对“虚数”的定义：

虚数可以指不实的数字或并非表明具体数量的数字。——360百科

在数学中，虚数就是形如a+b*i的数，其中a,b是实数，且b≠0,i² = - 1。虚数这个名词是17世纪著名数学家笛卡尔创立，因为当时的观念认为这是真实不存在的数字。后来发现虚数a+b*i的实部a可对应平面上的横轴虚部b与对应平面上的纵轴，这样虚数a+b*i可与平面内的点(a,b)对应。——360百科

然后是百科对“复数”的定义：

复数x被定义为二元有序实数对(a,b) ，记为z=a+bi,这里a和b是实数，i是虚数单位。在复数a+bi中，a=Re(z)称为实部，b=Im(z)称为虚部。当虚部等于零时，这个复数可以视为实数;当z的虚部不等于零时，实部等于零时，常称z为纯虚数。复数域是实数域的代数闭包，也即任何复系数多项式在复数域中总有根。复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

正如上文所说，一个复数可以看成是“复平面”上的一个点。复平面就是以实数部为x轴，以虚部为y轴所组成的类似“直角坐标系”的一个平面坐标体系。同样，我们也可以用“极坐标”来表示一个平面中的点。

复平面效果

上图就是在这个复平面上的一个点的三种表示方法。

然后，思考一个简单的问题：两个复数的乘法有没有某种特定的几何意义？（只是一个数学性质，在此不进一步深究，可用三角函数证明。）

两个复数相乘

两复数相乘，“长度相乘，极角相加”。不难想象如果两个复数它们到“坐标原点”的距离都是1，那么它们的乘积到坐标原点的距离还是一，只不过是绕着原点进行了旋转。

5.单位复根

现在，回到我们刚才讲到的“点值表示法”的问题，考虑这样一个问题，如果我有两个用点值表示的多项式，如何表示它们两个多项式的乘积呢？（假设这两个多项式选取的所有点的x值恰好相同。）

f (x) = {(x_{0}, f (x_{0})), (x_{1}, f (x_{1})), (x_{2}, f (x_{2})), . ., (x_{n}, f (x_{n}))}

$f(x)=\{(x_0,f(x_0)),(x_1,f(x_1)),(x_2,f(x_2)),..,(x_n,f(x_n))\}$

g (x) = {(x 0, g (x 0)), (x 1, g (x 1)), (x 2, g (x 2)), . ., (x n, g (x n))}

$g(x)=\{(x_0,g(x_0)),(x_1,g(x_1)),(x_2,g(x_2)),..,(x_n,g(x_n))\}$

点值表示两个多项式

如果 $F(x)=f(x) \times g(x)$ ，那么就有 $F(x_0)=f(x_0)*g(x_0)$ （ $x_0$ 为任意数）。也就是说，如果我把两个函数的点值表示法中的 $x$ 值相同的点的y值乘在一起就是它们的乘积（新函数）的点值表示。（这是一个 $O(n)$ 的操作。）

f (x) \times g (x) = {(x 0, f (x 0) g (x 0)), (x 1, f (x 1) g (x 1)), (x 0, f (x 2) g (x 2)), . ., (x n, f (x n) g (x n))}

$f(x)\times g(x)=\{(x_0,f(x_0)g(x_0)),(x_1,f(x_1)g(x_1)),(x_0,f(x_2)g(x_2)),..,(x_n,f(x_n)g(x_n))\}$

新函数的点值表示法

但是我们要的是系数表达式，而不是点制表达式，如果用高斯消元暴力地去解一个“n+1元方程组”恐怕就要把时间复杂度拉回 $O(n^2)$ （甚至更高）。为什么呢？因为当我们计算 $x_0，x_0^2，...，x_0^n$ 时会浪费大量的时间。这个数学运算看似是没有办法加速的，而实际上我们可以找到一种神奇的“x值”，带进去之后不用反复地去做无用n次方操作。我能想到的第一个数就是“1”，因为1的几次方都是1。然后我能想到的数就是“-1”，因为“-1”的平方是1。把这样的数带进去就可以减少我们的运算次数。

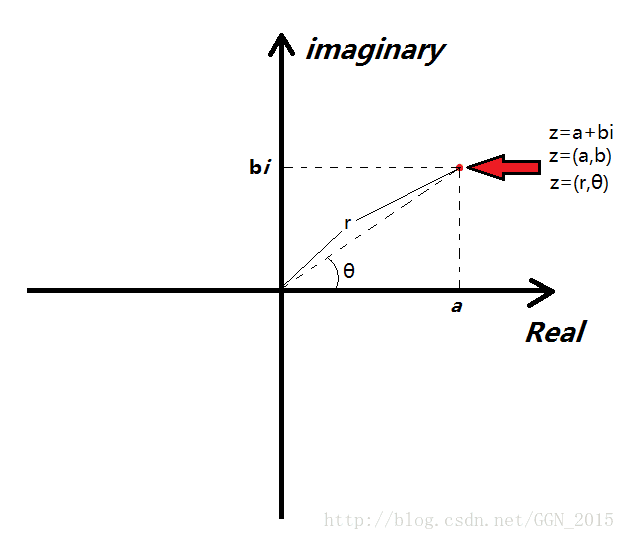
但是问题又来了，我们只有“-1”和“1”两个数，但是我们要至少带进去n+1个不同的数才能进行系数表示。考虑一个问题：也许“虚数”可能会帮上我们大忙。我们需要的是满足“ $\omega ^k=1$ ”的数（k为整数），然后我们就会发现“i”好像也满足这个条件：i*i=-1，（i*i）*（i*i）=1=i^4，当然“-i”也有这个性质。然而仅仅4个数还是不能满足我们的需求。

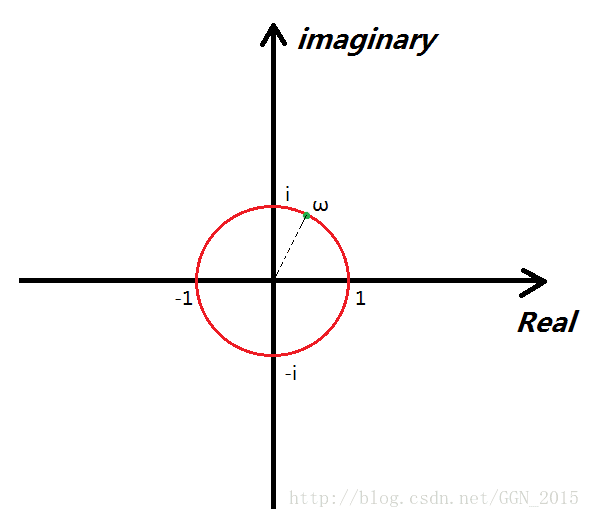
单位复根图

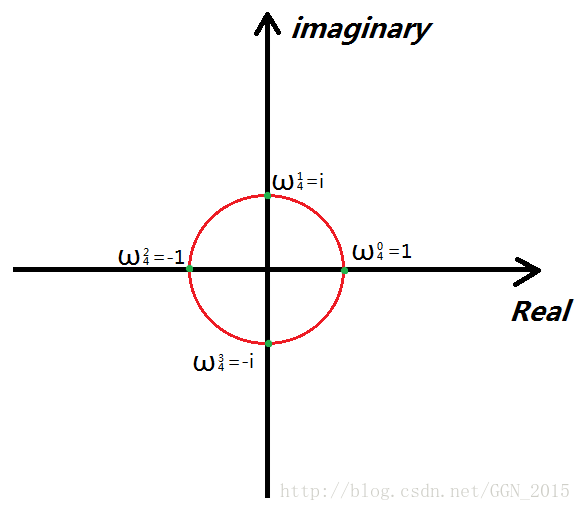
看上图中的红圈，红圈上的每一个点距原点的距离都是1个单位长度，所以说如果说对这些点做k次方运算，它们始终不会脱离这个红圈。因为它们在相乘的时候r始终=1，只是θ的大小在发生改变。而这些点中有无数个点经过若干次方之后可以回到“1”。因此，我们可以把这样的一组神奇的x带入函数求值。

像这种能够通过k次方运算回到“1”的数，我们叫它“复根”用“ω”表示。如果 $\omega ^k=1$ ，那么我们称“ $\omega$ 为1的k次复根”计做“ $\omega_k^n$ ”:

单位复根地表示

其中“n”就是一个序号数，我们把所有的“负根”按照极角大小逆时针排序从零开始编号。以“四次负根”“ $\omega_4^n$ ”为例：

ωn（4）

你会发现：其实k次负根就相当于是给图中的圆周平均分成k个弧，弧与弧之间的端点就是“复根”，另外 $\omega_4^2=-1=i^2=(\omega_4^1)^2,\omega_4^3=-i=i^3=(\omega_4^1)^3$ ， $\omega_4^0$ 是这个圆与“Real”轴正半轴的交点，所以无论k取多少， $\omega_4^0$ 始终=1。我们只需要知道 $\omega_4^1$ ，就能求出 $\omega_k^n$ ，所以我们称“ $\omega_k^1$ ”为“单位复根”。

其实，我们用“ $\omega_k$ ”表示单位复根， $\omega_k^1$ 表示的是“单位复根”的“1次方”也就是它本身,其他的就叫做k次单位复根的n次方。

k次单位复根

6.FFT的主要流程之DFT

说了这么多了，终于说到FFT了。FFT运用到了一种分治的思想，分治地去求当x=ω(k)[n]时整个多项式的值（永远都不要忘了每一个步骤的目的是什么）。你可以把一个多项式分成奇数次数项，和偶数次数项两部分，然后再用分治的思想去处理它的“奇数次项”和“偶数次项”。

FFT的二分过程

我们用DFT(F(x))[k]表示当x=ω^k时F(x)的值，所以有：DFT(F(x))[k]=DFT(G(x^2))[k]+ω^k*DFT(H(x^2))，也就是：

递归表达式

（把当前单位复根的平方分别以DFT的方式带入G函数和H函数求值。）

但是这个二分最大的局限就是只能处理长度为2的整数次幂的多项式，因为如果长度不为的整数次幂，二分到最后就会出现左半部分右半部分长度不一致的情况（导致程序取不到系数而爆炸），所以我们在做第一次DFT之前一定要把这个多项式补成长度为2^n（n为整数）的多项式（补上去的高次项系数为“0”），长度为2^n的多项式的最高次项为2^n-1次项。当我们向这个式子中“带入数值”的时候，一定要保证我带入的每个数都是不一样的，所以要带入1的2^n的单位复根的各个幂（因为1的2^n复根恰好有2^n个）。

【2018.6.30】我觉得上面这一段内容讲得还不够清晰，如果同学们没明白这段话的意思，可以先跳到后面“关于DFT的再次思考”，看看那里的讲解。看完以后再回到这里，继续阅读。

但是这个算法还需要从“分治”的角度继续优化。我们每一次都会把整个多项式的奇数次项和偶数次项系数分开，一只分到只剩下一个系数。但是，这个递归的过程需要更多的内存。因此，我们可以先“模仿递归”把这些系数在原数组中“拆分”，然后再“倍增”地去合并这些算出来的值。然而我们又要如何去拆分这些数呢？

递归拆分的方式

貌似并没有什么规律可循，但实际上你可要看仔细了，把这些下标都转化成二进制看看吧：

二进制翻转

是不是发现了一些神奇的特点：“拆分”之后的序列的下标恰好为长度为3位的二进制数的翻转。也就是说我们对原来的每个数的下标进行长度为三的二进制翻转就是新的下标。而为什么是长度为3呢？因为8=2^3。为了证明这一点，我们可以再举一个简单例子（它还是成立的）：

再举一个简单的翻转的例子

（一个数学性质，在此不再证明。我感觉这个原理有点像是“基数排序”，感兴趣的同学可以去看看。）

关于二进制翻转是如何实现的，本文中并没有介绍，强烈建议看一下这篇文章：

学习链接：补充——FFT中的二进制翻转问题

7.FFT的主要流程之IDFT

我们先整理一下思路，IDFT是做什么的？IDFT（傅里叶反变换）就是把一个用“点值表示法”表示的多项式，转化成一个用“系数表示法”表示的多项式，但是这似乎并不是很容易。然而其实我们刚刚恰好做了一些非常机智的事情——把“单位复根”的若干次方带入了原多项式。我们可以表示一下这些多项式（这里使用一个矩阵表示，不会的建议自学）。

DFT矩阵

如果我们想把这个表达式还原成只含有“a系数”的矩阵，那么就要在中间那个“巨大的矩阵”身上乘上一个它的“反矩阵”（反对称矩阵）就可以了。这个矩阵的中有一种非常特殊的性质，对该矩阵的每一项取倒数，再除以n就可以得到该矩阵的反矩阵。而如何改变我们的操作才能使计算的结果文原来的倒数呢？这就要看我们求“单位复根的过程了”：根据“欧拉函数”e^iπ=-1，我么可以得到e^2πi=1。如果我要找到一个数，它的k次方=1，那么这个数ω[k]=e^(2πi/k)（因为(e^(2πi/k))^k=e^(2πi)=1）。而如果我要使这个数值变成“1/ω[k]”也就是“(ω[k])^-1”，我们可以尝试着把π取成-3.14159…，这样我们的计算结果就会变成原来的倒数，而其它的操作过程与DFT是完全相同的（这真是极好的）。我们可以定义一个函数，向里面掺一个参数“1”或者是“-1”，然后把它乘到“π”的身上。传入“1”就是DFT，传入“-1”就是IDFT，十分的智能。

机房学长的代码写得实在是太好了Orz，忍不住引用了一下：

下面的代码来自 Leo的《FFT与多项式乘法》

欢迎同学们一同Orz ↑

这是整个代码的一个局部（出于礼貌，保留了原有的代码格式，但是加了一些注释）：

int rev[maxl];
void get_rev(int bit)//bit表示二进制位数,计算一个数在二进制翻转之后形成的新数
{
    for(int i=0;i<(1<<bit);i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
void fft(cd *a,int n,int dft)//n表示我的多项式位数
{
    for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
    //中间的那个if保证了每个数做多只被交换了1次
    //如果不写那么会有一些数被交换两次,导致最终的位置没有变
    for(int step=1;step<n;step<<=1)//模拟一个合并的过程
    {
        cd wn=exp(cd(0,dft*PI/step));//计算当前单位复根
        for(int j=0;j<n;j+=step<<1)
        {
            cd wnk(1,0);//计算当前单位复根
            for(int k=j;k<j+step;k++)
            {//蝴蝶操作
                cd x=a[k];
                cd y=wnk*a[k+step];
                a[k]=x+y;//这就是上文中F(x)=G(x)+ωH(x)的体现
                a[k+step]=x-y;
                    //后半个“step”中的ω一定和“前半个”中的成相反数
                    //“红圈”上的点转一整圈“转回来”，转半圈正好转成相反数
                wnk*=wn;
            }
        }
    }
    if(dft==-1) for(int i=0;i<n;i++) a[i]/=n;
    //考虑到如果是IDFT操作,整个矩阵中的内容还要乘上1/n  
}

关于DFT的再次思考

2018.6.29 我最近有思考了一些关于DFT原理的问题，觉得之前讲得有些草率，决定再写一个表述更清晰一些的版本。每个人都有适合的自己讲课风格，如果没看懂上面的讲解，不妨试试看看这里。

说到DFT（离散傅里叶变换）这个环节，就必须先说这个环节的目的。做音频处理的人用这个过程来实现值域与频域的转换，而我们OIer主要是为了把一个用系数表示法表示的函数转化为一个用点值表示法表示的函数。

我在前文中提到了一类神奇的数——单位复根，并且了解了关于它的一些性质：
1.我们通常用 $\omega_n = e^{\frac{2\pi i}{n}}$ 表示n次单位复根（的一次方）

2.n次单位复根的值随指数变化而循环，有 $\omega_n^{n+k}=\omega_n^k$ ，（也就是说k为整数时， $\omega_n^k$ 恰有n种不同的取值，分别为 $\omega_n^0,\omega_n^1,\omega_n^2,...,\omega_n^{n-1}$ ，k等于其余整数值时，都可以通过几次+n或者-n 平移到这个区间里）

3.折半引理： $\omega_n^k = e^{\frac{2\pi i}{n} \cdot k} = e^{\frac{2\pi i}{\frac{n}{2}} \cdot \frac{k}{2}} = \omega_{\frac{n}{2}}^{\frac{k}{2}}$ ，这个性质一会儿会用到，一定要理解透彻。

一个n-1次多项式可以用n个系数去描述，也可以用函数上的n个点去描述，n+1个点当然也可以，但是多余。根据上述2号结论，我们知道n次复根恰好有n种不同的取值，那我们不妨就把这n个不同的值带入多项式。

这样实际上，问题就转化成——把一个长度为n的向量A，变换成另一个长度为n的向量B。（我们记A与B的下标从0开始，到n-1结束，共n个位置。）

其中：
A 为系数向量， $A_k$ 中储存原多项式中 $x^k$ 项前的系数。
B 为点值向量， $B_k$ 中储存 $x = \omega_n^k$ 时原多项式的值。

为了描述方便，我们称 B向量为多项式 $A_0 + A_1x + A_2 x^2 +...+A_{n-1}x^{n-1}$ 的变换结果。

根据这个定义，我们可以表示出B向量某一个位置k上的值 $B_k$ ：

$B_k = A_0 + A_1 \cdot (\omega_n^k) + A_2 \cdot(\omega_n^k)^2 + A_3 \cdot(\omega_n^k)^3+...+A_{n-1}\cdot(\omega_n^k)^{n-1}$

我们不妨假设n为偶数（因为多向式可以在最后补上一些系数为0的高次项，所以这一假设对运算结果没有影响），我们把这个多项式的奇数次项和偶数次项分开，看看会不会得到一些惊人的结论。

推导（因为n为偶数，所以n-2为偶数、n-1为奇数）：

$B_k = (A_0+A_2\cdot(\omega_n^k)^2+ A_4 \cdot (\omega_n^k)^4...+A_{n-2}\cdot(\omega_n^k)^{n-2}) +(A_1\cdot(\omega_n^k)+A_3\cdot(\omega_n^k)^3+A_5\cdot(\omega_n^k)^5+...+A_{n-1}\cdot(\omega_n^k)^{n-1})$

看着不“对称”，把右半部分（也就是所有奇数项）都提出一个 $\omega_n^k$ 来：

$B_k = (A_0+A_2\cdot(\omega_n^k)^2+ A_4 \cdot (\omega_n^k)^4...+A_{n-2}\cdot(\omega_n^k)^{n-2}) +\omega_n^k\cdot(A_1+A_3\cdot(\omega_n^k)^2+A_5\cdot(\omega_n^k)^4+...+A_{n-1}\cdot(\omega_n^k)^{n-2})$

这次，左半部分和右半部分的指数得到了统一，都是0次到n-2次，也就是都是偶数了（后面还会用到这个偶数指数的性质）。

好像可以用一次折半引理，不用白不用，试试看:

$(\omega_n^k)^2=\omega_n^{2k} = \omega_{\frac{n}{2}}^{k}$

所以有：

$B_k = (A_0+A_2\cdot( \omega_{\frac{n}{2}}^{k})+ A_4 \cdot ( \omega_{\frac{n}{2}}^{k})^2...+A_{n-2}\cdot( \omega_{\frac{n}{2}}^{k})^{\frac{n}{2}-1}) +\omega_n^k\cdot(A_1+A_3\cdot( \omega_{\frac{n}{2}}^{k})^1+A_5\cdot( \omega_{\frac{n}{2}}^{k})^2+...+A_{n-1}\cdot( \omega_{\frac{n}{2}}^{k})^{\frac{n}{2}-1})$

诶？好像… $A_0+A_2\cdot( \omega_{\frac{n}{2}}^{k})+ A_4 \cdot ( \omega_{\frac{n}{2}}^{k})^2...+A_{n-2}\cdot( \omega_{\frac{n}{2}}^{k})^{\frac{n}{2}-1}$ 这个式子不就是多项式 $A_0+A_2\cdot x+ A_4 \cdot x^2...+A_{n-2}\cdot x^{\frac{n}{2}-1}$ 在 $x = \omega_{\frac{n}{2}}^{k}$ 处的点值吗？右半部分？右半部分好像也很像，像是多项式 $A_1+A_3\cdot x+ A_5 \cdot x^2...+A_{n-1}\cdot x^{\frac{n}{2}-1}$ 在 $x = \omega_{\frac{n}{2}}^{k}$ 处的点值。而且这两个多项式都恰好有 $\frac{n}{2}$ 项。

把n个n次复根带入一个长度为n的多项式，是我们要做的DFT过程，那把n/2个 n/2次复根带入一个长度为n/2的多项式，是不是也可以看成是DFT？

假如我们已经知道了多项式 $A_0+A_2\cdot x+ A_4 \cdot x^2...+A_{n-2}\cdot x^{\frac{n}{2}-1}$ 的变换结果为长度为n/2的向量L，多项式 $A_1+A_3\cdot x+ A_5 \cdot x^2...+A_{n-1}\cdot x^{\frac{n}{2}-1}$ 的9 变换结果 （变换结果一词在前文中有定义）为长度为n/2的向量R，实际上B向量中的任意一个位置就可以O(1)算出了（接下来我们说具体怎么 O(1) 求）。

因为根据上文的定义有： $B_k = L_k + \omega_n^k \cdot R_k$ ，其中 $0\leq k < \frac{n}{2}$ ，因为L和R的长度只有 $\frac{n}{2}$ 。这种方法可以求出B向量的左半部分。那右半部分该怎么求呢？

其实还有这样一个式子, $B_{\frac{n}{2}+k}=L_k - \omega_n^k \cdot R_k$ ，其中 $0\leq k < \frac{n}{2}$ 。

我们知道 $\omega_n^{\frac{n}{2}+k}=\omega_n^k \cdot \omega_n^{\frac{n}{2}}= \omega_n^k \cdot e^{\frac{2\pi i}{n}\cdot\frac{n}{2}} = \omega_n^k\cdot e^{\pi i} = - \omega_n^k$ 。

前文中我们提过一嘴， $B_k = (A_0+A_2\cdot(\omega_n^k)^2+ A_4 \cdot (\omega_n^k)^4...+A_{n-2}\cdot(\omega_n^k)^{n-2}) +\omega_n^k\cdot(A_1+A_3\cdot(\omega_n^k)^2+A_5\cdot(\omega_n^k)^4+...+A_{n-1}\cdot(\omega_n^k)^{n-2})$

这个式子中，除了奇数次项提出的一个 $\omega_n^k$ 外，其余所有关于 $\omega_n^k$ 的项都是偶数次项。一个数的平方与其相反数的平方一定相等，一个数的偶次方与其相反数的偶次方也一定相等。 $\omega_n^{\frac{n}{2}+k}= - \omega_n^k$ 而，这就说明，在对B向量右半部分的求解中，我们仍然可以在L向量和R向量中得到我们想要的结果。

综上，有：

$B_k = L_k + \omega_n^k \cdot R_k$ ，其中 $0\leq k < \frac{n}{2}$
$B_{\frac{n}{2}+k}=L_k - \omega_n^k \cdot R_k$ ，其中 $0\leq k < \frac{n}{2}$

我们把这个通关过 L和R 求解 B 的方法称为 信息合并 。

同理，我们想要求解L向量和R向量，继续递归即可，把一个长度为 $\frac{n}{2}$ 的多项式分成两个长度为 $\frac{n}{4}$ 的多项式，然后进行DFT，再进行信息合并。递归直到到多项式长度为1为止（因为长度为1的多项式只有常数项，变换结果就是其本身。）

这就是这个算法的主要思想，但是思想与代码之间还是有很大的差距的，我知道很多同学看不懂上面的代码，我在这里解释一下这个代码的实现机理。

有关FFT算法实现机理的再讨论

每一次递归，我们都要求被处理的多项式的项数是偶数（或者是1），那么我们不妨先在多项式系数表示法尾部补0，把它的长度补成一个2的整数次幂，这样每次都可以继续分治（因为整个多项式的长度不会超过原多项式的二倍，所以时间复杂度不变）。

为了节省空间，我们从头到尾只使用一个长度为n的数组arr（下标也是从0到n-1）来实现整个DFT的过程，最开始的时候我们用arr储存A。

接下来的内容表示arr数组中内容的“变迁”。

a r r = {A 0, A 1, . . ., A n 2 - 1, A n 2, A n 2 + 1, . . ., A n - 1}

$arr = \{A_0,A_1,...,A_{\frac{n}{2}-1}, A_{\frac{n}{2}},A_{\frac{n}{2}+1},...,A_{n-1}\}$

奇数偶数分项：

a r r = {A 0, A 2, . . ., A n - 2, A 1, A 3, . . ., A n - 1}

$arr = \{A_0, A_2, ..., A_{n-2}, A_1, A_3, ..., A_{n-1}\}$

递归计算，直接把计算结果L和R覆盖到原数组对应的位置上

a r r = {L 0, L 1, . . ., L n 2 - 1, R 0, R 1, . . ., R n 2 - 1}

$arr = \{L_0 ,L_1, ..., L_{\frac{n}{2}-1}, R_0, R_1, ..., R_{\frac{n}{2}-1}\}$

最后信息合并，得到：

a r r = {B 0, B 1, . . ., B n 2 - 1, B n 2, B n 2 + 1, . . ., B n - 1}

$arr = \{B_0,B_1,...,B_{\frac{n}{2}-1}, B_{\frac{n}{2}},B_{\frac{n}{2}+1},...,B_{n-1}\}$

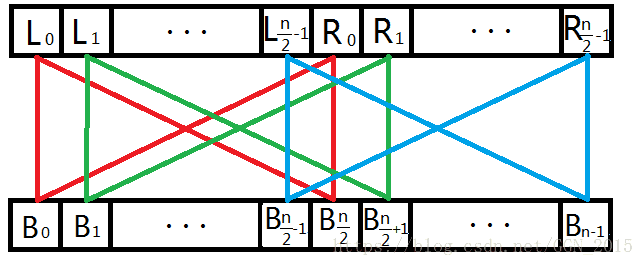
信息合并，又叫做蝴蝶操作，它为什么会有这么美丽的一个名字呢，我想用一个图来谈谈我的见解。

蝴蝶操作

我们根据上文关于信息合并的推导可知， $L_0$ 和 $R_0$ 只决定 $B_0$ 和 $B_{\frac{n}{2}}$ ， $L_1$ 和 $R_1$ 只决定 $B_1$ 和 $B_{\frac{n}{2}+1}$ ，…， $L_k$ 和 $R_k$ 只决定 $B_k$ 和 $B_{\frac{n}{2}+k}$ 。所以，我们可以直接把 $B_k$ 和 $B_{\frac{n}{2}+k}$ 的值覆盖到 $L_k$ 和 $R_k$ 的位置上（而且发现它们恰好在数组上的位置也是对应的）。

我们用一个变量k从0循环到 $\frac{n}{2}-1$ ，每次计算如下两个值：

x = L k, y = ω k n \cdot R k

$x = L_k, y = \omega_n^k\cdot R_k$

这样就有：

B k = x + y, B n 2 + k = x - y

$B_k = x+y, B_{\frac{n}{2}+k}=x-y$

而 $\omega_n^k = \omega_n^{k-1} \cdot \omega_n$ ，是可以在循环的时候递推出来的。

而事实上，我们前面也讨论过，分治的过程是可以利用循环来实现的。我们先只奇数偶数分项，然后得到了下标二进制反转后的序列。（这两个词我没给定义，关于下表二进制反转的问题，我觉得第6节“FFT的主要流程之DFT”讲得挺明白的。）

然后，逐层实现信息的合并，第一层，把相邻的两个长度为1的变换结果，合并成一个长度为2的变换结果，信息块个数除以2。第二层，把相邻的两个长度为2的的变换结果，合并成一个长度为4的变换结果…这样我们只需要O(nlogn)的时间复杂度就可以求出整个多项式的变换结果（每层合并都需要花费O(n)的总时间代价，一共有O(logn)层合并）。

IDFT的实现原理不再赘述，见上文第7节“FFT的主要流程之IDFT”。

现在我把代码再贴一次：

int rev[maxl];
void get_rev(int bit)//bit表示二进制位数,计算一个数在二进制翻转之后形成的新数
{
    for(int i=0;i<(1<<bit);i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
}
void fft(cd *a,int n,int dft)//n表示我的多项式位数
{
    for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
    //中间的那个if保证了每个数做多只被交换了1次
    //如果不写那么会有一些数被交换两次,导致最终的位置没有变
    for(int step=1;step<n;step<<=1)//模拟一个合并的过程
    {
        cd wn=exp(cd(0,dft*PI/step));//计算当前单位复根
        for(int j=0;j<n;j+=step<<1)
        {
            cd wnk(1,0);//计算当前单位复根
            for(int k=j;k<j+step;k++)
            {//蝴蝶操作
                cd x=a[k];
                cd y=wnk*a[k+step];
                a[k]=x+y;//这就是上文中F(x)=G(x)+ωH(x)的体现
                a[k+step]=x-y;
                    //后半个“step”中的ω一定和“前半个”中的成相反数
                    //“红圈”上的点转一整圈“转回来”，转半圈正好转成相反数
                    //一个数相反数的平方与这个数自身的平方相等..
                wnk*=wn;
            }
        }
    }
    if(dft==-1) for(int i=0;i<n;i++) a[i]/=n;
    //考虑到如果是IDFT操作,整个矩阵中的内容还要乘上1/n  
}

感觉我一年前写的注释虽然不是很清晰，但是还是蛮正确的，就没有改动。希望同学们能有一个更深入的理解~

8.后记

最后总结一下FFT的优化思想：

FFT的优化思想图

然后是FFT的优化理念：

FFT的优化理念

（完全自创，如有雷同，纯属巧合，尽管并没什么用。）

FFT其实还可以用来计算BIGNUM乘法，因为我们可以把一个长整数理解成a[0]+a[1]*10+a[2]*10^2+…+a[n]*10^n。把“10”当成未知数，这个多项式每一个次方项的系数就是BIGNUM每一数位上的数。而这时，数组长度“n”就不能单纯的取这个十进制数的长度，而要取大于等于两个十进制数长度加和的最小的2的正整数次幂。因为我们要保证DFT得到的离散点的个数足够表示我最终生成的新多项式（也就是取的点的个数要大于等于这个结果多项式的长度）。

总之，这真的是一个很好的算法，但是要注意，除题中的数据范围（多项式长度）超过了10^4，否则暴力是可以解决的。而且FFT常数巨大，请同学们一定要慎用！慎用！慎用！

写了一整天，可算是把这篇长篇大论的博客写完了。FFT就是一个典型的用数学方法对问题实现优化的方法。DFT对数学基础要求很高，但是信息学与数学的联系是相当紧密的，所以这种情况时常会出现。数学不好的同志们一定要加油哦~

赶稿匆忙，如有谬误，望同学们谅解。

2017.11.19【补】第一次自己手写FFT，感觉很开心

#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<complex>
using namespace std;

typedef complex<double> cd;//复数类的定义
const int maxl=2094153;//nlogn的最大长度(来自leo学长的博客)
const double PI=3.14159265358979;//圆周率,不解释

cd a[maxl],b[maxl];//用于储存变换的中间结果
int rev[maxl];//用于储存二进制反转的结果
void getrev(int bit){
    for(int i=0;i<(1<<bit);i++){//高位决定二进制数的大小
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
    }//能保证(x>>1)<x,满足递推性质
}

void fft(cd* a,int n,int dft){//变换主要过程
    for(int i=0;i<n;i++){//按照二进制反转
        if(i<rev[i])//保证只把前面的数和后面的数交换,(否则数组会被翻回来)
            swap(a[i],a[rev[i]]);
    }
    for(int step=1;step<n;step<<=1){//枚举步长的一半
        cd wn=exp(cd(0,dft*PI/step));//计算单位复根
        for(int j=0;j<n;j+=step<<1){//对于每一块
            cd wnk(1,0);//!!每一块都是一个独立序列,都是以零次方位为起始的
            for(int k=j;k<j+step;k++){//蝴蝶操作处理这一块
                cd x=a[k];
                cd y=wnk*a[k+step];
                a[k]=x+y;
                a[k+step]=x-y;
                wnk*=wn;//计算下一次的复根
            }
        }
    }
    if(dft==-1){//如果是反变换,则要将序列除以n
        for(int i=0;i<n;i++)
            a[i]/=n;
    }
}

int output[maxl];
char s1[maxl],s2[maxl];
int main(){
    scanf("%s%s",s1,s2);//读入两个数
    int l1=strlen(s1),l2=strlen(s2);//就算"次数界"
    int bit=1,s=2;//s表示分割之前整块的长度
    for(bit=1;(1<<bit)<l1+l2-1;bit++){
        s<<=1;//找到第一个二的整数次幂使得其可以容纳这两个数的乘积
    }
    for(int i=0;i<l1;i++){//第一个数装入a
        a[i]=(double)(s1[l1-i-1]-'0');
    }
    for(int i=0;i<l2;i++){//第二个数装入b
        b[i]=(double)(s2[l2-i-1]-'0');
    }
    getrev(bit);fft(a,s,1);fft(b,s,1);//dft
    for(int i=0;i<s;i++)a[i]*=b[i];//对应相乘
    fft(a,s,-1);//idft
    for(int i=0;i<s;i++){//还原成十进制数
        output[i]+=(int)(a[i].real()+0.5);//注意精度误差
        output[i+1]+=output[i]/10;
        output[i]%=10;
    }
    int i;  
    for(i=l1+l2;!output[i]&&i>=0;i--);//去掉前导零
    if(i==-1)printf("0");//特判长度为0的情况
    for(;i>=0;i--){//输出这个十进制数
        printf("%d",output[i]);
    }
    putchar('\n');
    return 0;
}

[2017.12.1]在此补充一下NTT（快速数论变换）的多项式乘法的代码。

#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
//#include<complex>
using namespace std;
//typedef complex<double> cd;

typedef long long LL;

void exgcd(int a,int b,int& x,int& y){
    if(b==0){
        x=1;
        y=0;
        return;
    }
    int x0,y0;
    exgcd(b,a%b,x0,y0);
    x=y0;y=x0-int(a/b)*y0;
}

int Inv(int a,int p){
    int x,y;
    exgcd(a,p,x,y);
    x%=p;
    while(x<0)x+=p;
    return x;
}

int qpow(int a,int b,int p){
    if(b<0){
        b=-b;
        a=Inv(a,p);
    }
    LL ans=1,mul=a%p;
    while(b){
        if(b&1)ans=ans*mul%p;
        mul=mul*mul%p;
        b>>=1;
    }
    return ans;
}

#define maxn (65537*2)
const int MOD=479*(1<<21)+1,G=3;

int rev[maxn];
void get_rev(int bit){
    for(int i=0;i<(1<<bit);i++){
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
    }
}

//from internet
//for(int i=0; i<NUM; i++)  
//{  
//    int t = 1 << i;  
//    wn[i] = quick_mod(G, (P - 1) / t, P);  
//}  

LL a[maxn],b[maxn];
void ntt(LL* a,int n,int dft){
    for(int i=0;i<n;i++){
        if(i<rev[i])
            swap(a[i],a[rev[i]]);
    }
    for(int step=1;step<n;step<<=1){
        LL wn;
        wn=qpow(G,dft*(MOD-1)/(step*2),MOD);
        for(int j=0;j<n;j+=step<<1){
            LL wnk=1;//这里一定要用long long不然会迷之溢出
            for(int k=j;k<j+step;k++){
                LL x=a[k]%MOD,y=(wnk*a[k+step])%MOD;//这里也要用long long
                a[k]=(x+y)%MOD;
                a[k+step]=((x-y)%MOD+MOD)%MOD;
                wnk=(wnk*wn)%MOD;
            }
        }
    }
    if(dft==-1){
        int nI=Inv(n,MOD);
        for(int i=0;i<n;i++)
            a[i]=a[i]*nI%MOD;
    }
}

#include<cstring>
char s1[maxn],s2[maxn];

int main(){
    //scanf("%*d");
    scanf("%s%s",s1,s2);
    int l1=strlen(s1),l2=strlen(s2);
    for(int i=0;i<l1;i++)a[i]=s1[l1-i-1]-'0';
    for(int i=0;i<l2;i++)b[i]=s2[l2-i-1]-'0';
    int bit,s=2;
    for(bit=1;(1<<bit)<(l1+l2-1);bit++)s<<=1;
    get_rev(bit);ntt(a,s,1);ntt(b,s,1);
    for(int i=0;i<s;i++)
        a[i]=a[i]*b[i]%MOD;
    ntt(a,s,-1);
    for(int i=0;i<s;i++){
        a[i+1]+=a[i]/10;
        a[i]%=10;
    }
    int cnt=s;
    while(cnt>=0 && a[cnt]==0)cnt--;
    if(cnt==-1)printf("0");
    for(int i=cnt;i>=0;i--){
        printf("%d",a[i]);
    }
    putchar('\n');
    return 0;
}

最新更新

序言

前言