目录
认识堆的简单结构:
二叉树:
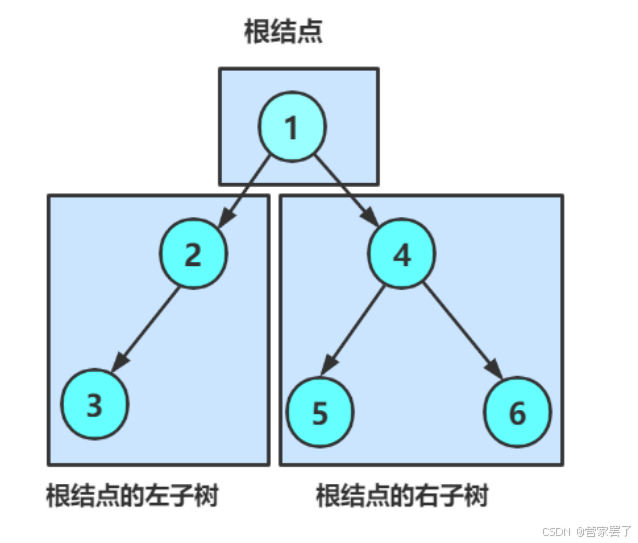
二叉树是一种每个节点最多有两个子节点的数据结构。每个节点包含一个值和指向两个子节点的指针,通常分别称为左子节点和右子节点。
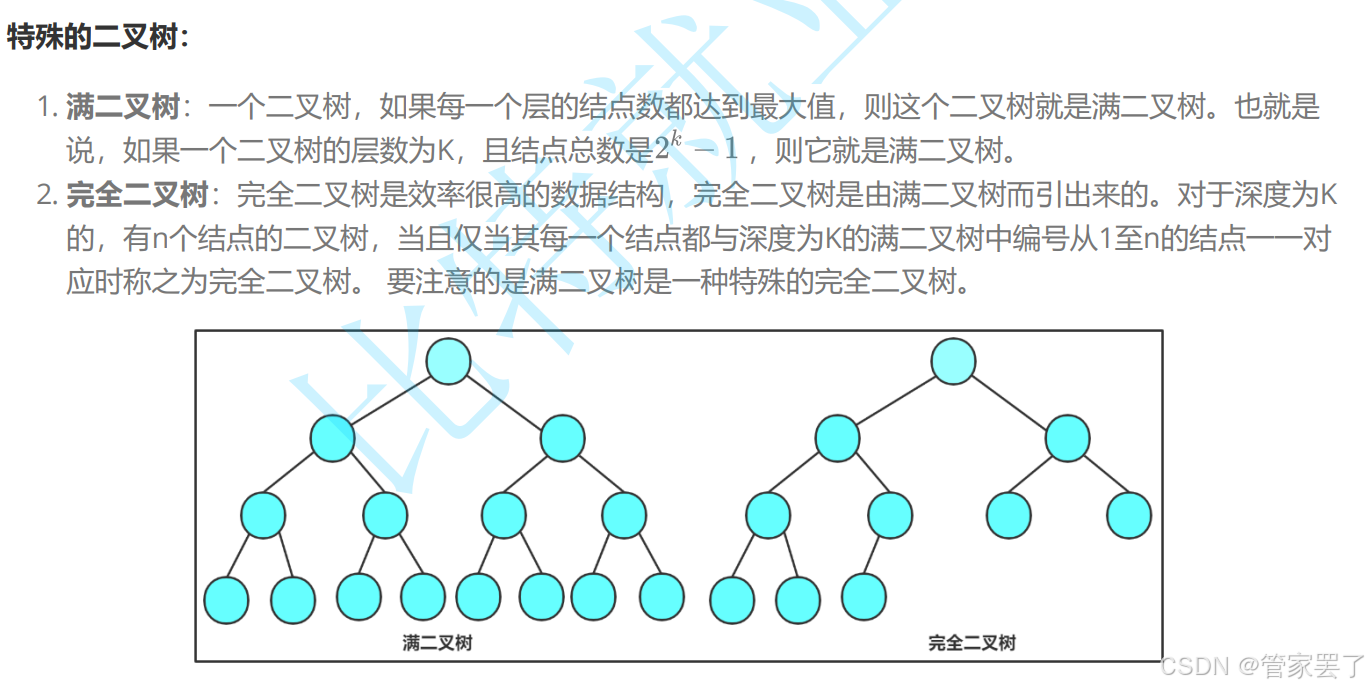
完全二叉树:
完全二叉树是一种特殊类型的二叉树,除了最后一层以外的每一层都被完全填满,最后一层的节点都集中在左边。(完全二叉树可以由顺序表实现,一会我会详细地进行讲解)
堆:
堆是一种完全二叉树。
大堆:
在“大堆”中,每个节点的值都大于或等于其子节点的值。也就是说,根节点的值是整个堆中的最大值。
小堆:
在“小堆”中,每个节点的值都小于或等于其子节点的值。也就是说,根节点的值是整个堆中的最小值。
完全二叉树可以由顺序表实现:
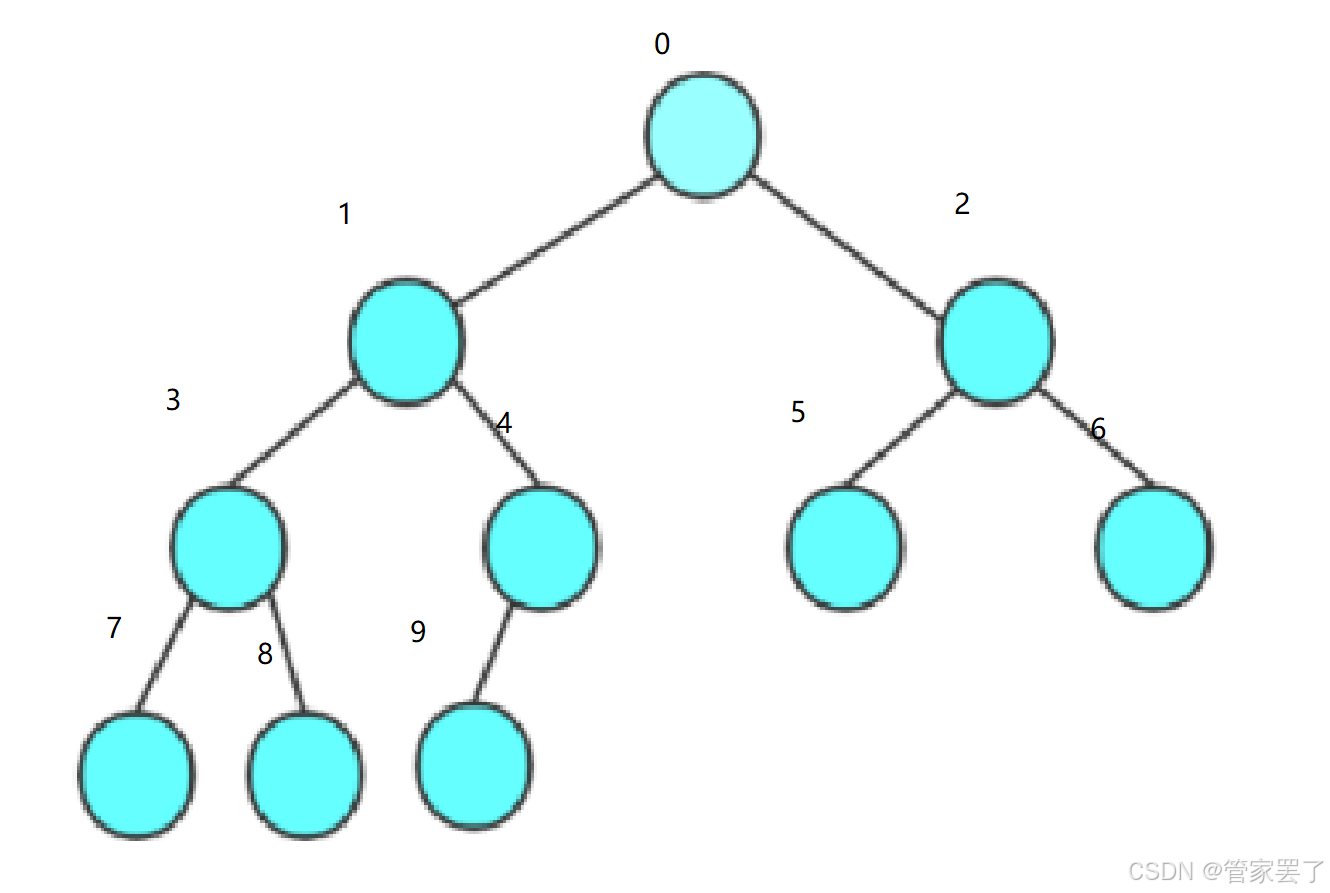
完全二叉树中:
1.假设一个根节点的下标为i,则它的两个子节点的下标分别为2i+1和2i+2,。
2.假设一个子节点的下标为i,则它所对应的根节点的下标为(i-1)/2。
正因为完全二叉树中根节点与子节点的下标之间存在某种特殊关系,所以完全二叉树可以由顺序表实现。
堆的常用接口(我们实现一个大堆):
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}HP;
//方便交换的函数
void Swap(HPDataType* p1, HPDataType* p2);
//向上调整
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int n, int parent);
//堆的初始化
void HPInit(HP* php);
//堆的销毁
void HPDestroy(HP* php);
//堆插入
void HPPush(HP* php, HPDataType x);
//堆顶数据的删除
void HPPop(HP* php);
// 取堆顶的数据
HPDataType HPTop(HP* php);
// 堆的判空
bool HPEmpty(HP* php);方便交换的函数:
因为我们在大堆中插入删除,会经常做数据交换,不然无法保证后来的堆还是个大堆,所以我们单独写出一个Swap函数,以便交换数据。
//方便交换的函数
void Swap(HPDataType* p1, HPDataType* p2)
{
HPDataType tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}堆的初始化:
//堆的初始化
void HPInit(HP* php)
{
php->a = (HPDataType*)malloc(4 * sizeof(HPDataType));
php->size = 0;
php->capacity = 4;
}堆的销毁:
//堆的销毁
void HPDestroy(HP* php)
{
free(php->a);
php->a = NULL;
php->size = php->capacity = 0;
}堆插入:
void HPPush(HP* php, HPDataType x)
{
if (php->capacity == php->size)
{
int newcapacity = 2 * php->capacity;
php->a = (HPDataType*)realloc(php->a, newcapacity * sizeof(HPDataType));
php->capacity = newcapacity;
}
php->a[php->size] = x;
php->size++;
AdjustUp(php->a,php->size-1);
}堆插入,可以先在堆尾插入,插入后再把堆尾数据向上调整即可。向上调整函数稍后会讲到。
堆顶数据的删除:
//堆顶数据的删除
void HPPop(HP* php)
{
Swap(&php->a[0], &php->a[php->size - 1]);
php->size--;
AdjustDown(php->a, php->size, 0);
}要删除堆顶数据,我们可以先把堆顶数据和堆尾数据进行交换,然后进行删除,删除后将之后的堆顶数据向下调整即可。向下调整稍后会讲到。
取堆顶数据:
// 取堆顶的数据
HPDataType HPTop(HP* php)
{
return php->a[0];
}堆的判空:
// 堆的判空
bool HPEmpty(HP* php)
{
return !(php->size);
}向上调整:
向上调整的接口主要接收顺序表的头指针,和想要向上调整的数据的下标。
//向上调整
void AdjustUp(HPDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child>0)
{
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
child = parent;
parent = (child - 1) / 2;
}
else
break;
}
}向上调整的主要思路是孩子节点和父亲节点去比大小,如果孩子比父亲大就要实行一次交换。就这样,孩子和父亲不断往完全二叉树的上方走、并且不断地进行比较和交换。最终就能实现此数据结构还是个大堆。
向下调整:
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{
int child = 2 * parent + 1;
while (child < n)
{
if (child + 1 < n && a[child] < a[child + 1])
{
child++;
}
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
parent = child;
child = 2 * parent + 1;
}
}
}向下调整过程中,先要比两个孩子的大小,挑出较大的那个孩子,然后父亲再和孩子比,如果父亲比孩子小,那么就交换父亲和孩子。就这样,孩子和父亲不断往完全二叉树的下方走、并且不断地进行比较和交换。最终就能实现此数据结构还是个大堆。