目录

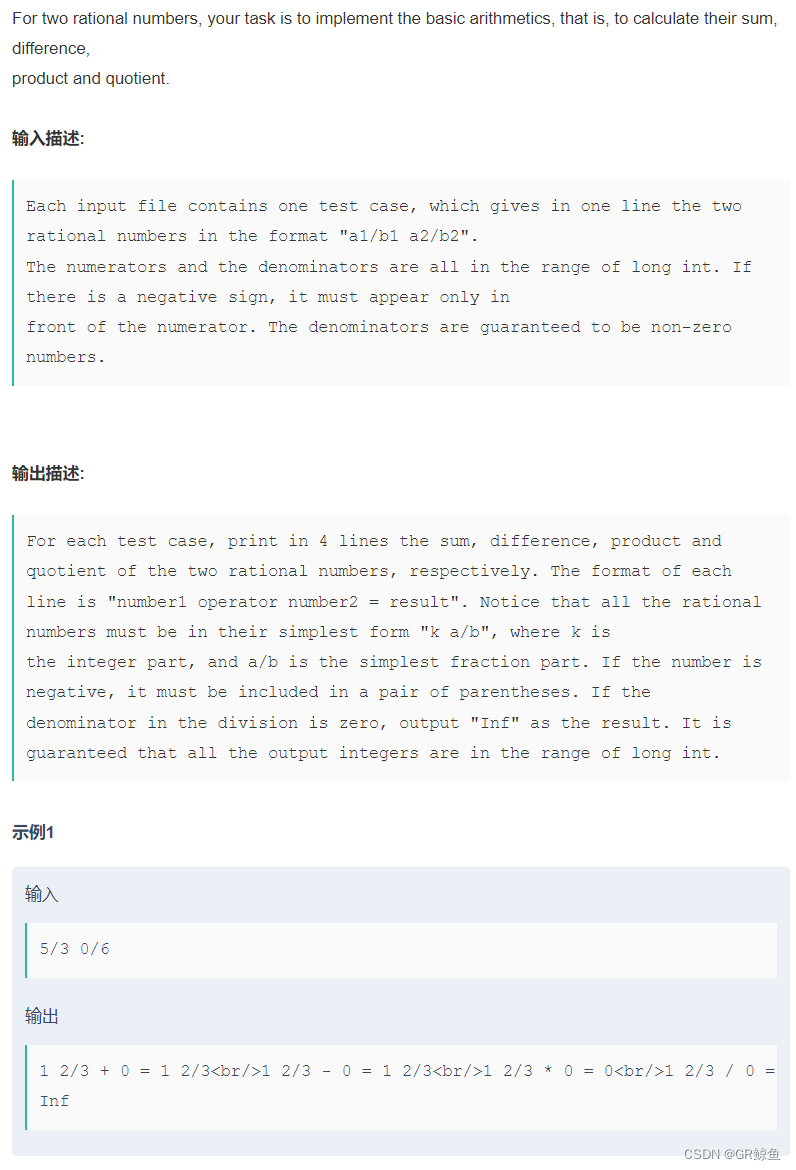
牛客_Rational Arithmetic（英文题模拟有理数运算）

解析代码

牛客_Rational Arithmetic（英文题模拟有理数运算）

Rational Arithmetic (20)__牛客网

解析代码

本题看上去不难，但是存在几个问题：

1. 除数为0，这个很好解决，做个判断即可。
2. 负数的输出，这个只要一个标签即可。
3. 题目中虽然没有明说，但是这个数字处理后其实是有可能不存在分数部分或者整数部分的。也就是说将数据处理完形成k a/b的格式后，有可能只有一个k，也可能只有一个a/b，也有可能两者皆有，所以要分别考虑这几种情况。

思路：

        可以尝试实现一个有理数类，将数据处理后重载一下加减乘除即可。处理数据的方法就是除一下mod一下的问题，加减乘除遵循基本的分数加减乘除原则，最后求一下最大公约数，做一下约分，再处理一下数据，就OK了。

#include <iostream>
using namespace std;

typedef long long int64;

class Rational
{
public:
	Rational(int64 n, int64 d)
	{
		negetive = false;
		isZero = false;
		if (0 == d) // 在输入时分母永远不可能为0，但是经过运算之后分母可能为0
		{
			isZero = true;
			return;
		}
		if (n < 0) // 分子小于0，表示为负数
		{
			negetive = !negetive;
		}
		if (d < 0) // 在输入时分母一定不会小于0， 但是经过计算之后分母也可能会小于0
		{
			negetive = !negetive;
		}
		// 如果分数是假分数，必须要将其化简为真分数 比如：5 / 3----> 1 2/3
		integer = n / d;
		numerator = n - integer * d;
		denominator = abs(d);
		// 如果不是最简的分数，还需要将其化简为最简的分数： 10 / 15 ----> 2 / 3
		// 只需给分子和分母分别除分子和分母最大公约数
		if (numerator < -1 || numerator > 1)
		{
			int gcd = CalcGCD(abs(numerator), denominator);
			if (gcd)
			{
				numerator /= gcd;
				denominator /= gcd;
			}
		}
		totalnumerator = integer * denominator + numerator;
	}
	Rational operator+(const Rational& r) const
	{
		int64 n = totalnumerator * r.denominator + r.totalnumerator * denominator;
		int64 d = denominator * r.denominator;
		return Rational(n, d);
	}
	Rational operator-(const Rational & r) const
	{
		int64 n = totalnumerator * r.denominator - r.totalnumerator * denominator;
		int64 d = denominator * r.denominator;
		return Rational(n, d);
	}
	Rational operator*(const Rational & r) const
	{
		int64 n = totalnumerator * r.totalnumerator;
		int64 d = denominator * r.denominator;
		return Rational(n, d);
	}
	Rational operator/(const Rational & r) const
	{
		int64 n = totalnumerator * r.denominator;
		int64 d = denominator * r.totalnumerator;
		return Rational(n, d);
	}
private:
	// 求最大公约数：辗转相除
	int64 CalcGCD(int64 a, int64 b) // 求最大公约数：辗转相除
	{
		return b ? CalcGCD(b, a % b) : a;
	}
	friend ostream& operator<<(ostream & _cout, const Rational & r)
	{
		if (r.isZero)
		{
			_cout << "Inf";
			return _cout;
		}
		if (0 == r.integer && 0 == r.numerator)
		{
			_cout << "0";
			return _cout;
		}
		if (r.negetive) // 如果是负数，需要用()括起来
		{
			_cout << "(-";
		}
		if (r.integer) // 输出有理数：整数 + 分数（整数: 可能存在也可能不存在）
		{
			_cout << abs(r.integer);
			if (r.numerator) // 如果分数部分存在，整数和分数之间有一个空格
			{
				_cout << " ";
			}
		}
		if (r.numerator) // 分数: 可能存在也可能不存在
		{
			_cout << abs(r.numerator) << "/" << r.denominator;
		}
		if (r.negetive)
		{
			_cout << ")";
		}
		return _cout;
	}
private:
	int64 numerator; // 分子
	int64 denominator; // 分母
	int64 integer; // 整数部分
	bool negetive; // 负数
	bool isZero; // 分母是否为0
	int64 totalnumerator; // 参与运算的分子：原分子 + 整数部分
};

int main()
{
	int64 n1, d1, n2, d2;
	while (scanf("%lld/%lld %lld/%lld", &n1,&d1,&n2,&d2) != EOF)
	{
		Rational r1(n1, d1);
		Rational r2(n2, d2);
		cout << r1 << " + " << r2 << " = " << r1 + r2 << endl;
		cout << r1 << " - " << r2 << " = " << r1 - r2 << endl;
		cout << r1 << " * " << r2 << " = " << r1 * r2 << endl;
		cout << r1 << " / " << r2 << " = " << r1 / r2 << endl;
	}
	return 0;
}